基于Radau II A法的电磁暂态并行计算

张 静，殷 明，叶 婧，李博文

(1. 三峡大学电气与新能源学院，湖北 宜昌 443002；2. 国网湖北省电力有限公司随州供电公司，湖北 随州 441300)

1 引言

随着现代电力电子技术的快速发展，越来越多的电力电子元件被运用到电力系统中，使得电力系统运行方式更加灵活、多变。但是随之而来的是更加复杂的控制方式以及更加快速的动态特性。针对于大规模多尺度的电力系统，为评估过电压、过电流对电力系统稳定性造成的影响，维持电网的安全平稳运行，电磁暂态过程的高效仿真显得极其重要[1]。

并行计算是电磁暂态高效快速仿真的有效手段之一。图形处理器(GPU)具有多核心、高集成度的特点[2]，结合所选算法特征，GPU被应用于电磁暂态并行计算中[3，4]，提高计算速度。

另一方面，大步长仿真也是提高电磁暂态仿真速度的重要手段。动态相量法可以在保持精度的同时使用大步长仿真，提高仿真速度[5]。而传统的动态相量由于存在谐波截断误差[6]，无法准确描述含有多种高次谐波系统的动态行为。因此文献[7，8]采用多频段动态相量应用在电磁暂态仿真中。

算法的多样性也为大步长仿真提供了可能性。隐式梯形法作为一种经典的离散方法被广泛的应用于电磁暂态计算中，具有二阶计算精度。但其仿真步长小，仿真速度慢，近年来，更多多级隐式的方法凭借着大步长仿真的优势被应用在电力系统计算中。但是多级就意味着雅克比矩阵增维，从而导致计算量增加，使得采用大步长仿真失去意义，因此多级隐式法并不适合直接应用于电磁暂态计算中。文献[9]将多级的广义向后差分方法应用于电磁暂态稳定性计算中，通过对大矩阵进行分块处理，减少计算量，得到可观的加速比。文献[10]也将一种多级的方法应用于电磁暂态计算中，通过并行处理三对角块矩阵，从而提高了计算速度。

而在众多的多级隐式方法中，2级3阶Radau II A法具有3阶计算精度，具有A稳定性和L稳定性[11]，属于时域仿真，和动态相量法相比不存在谐波截断误差。但若直接将Radau II A法应用于电磁暂态计算中，由于引入内点，会造成计算量倍增的问题。因此，将从并行的途径获得加速比。

概括起来，所提算法的创新点在于，利用Sherman-Morrison[12，13]公式求解代数方程，相比文献[13]，其得到的高维雅克比矩阵的非对角块为一个高度稀疏的常系数矩阵，因此避免了牛顿迭代中因更新雅克比矩阵而需要重新对其分解的过程。并且在求逆之前，先对大矩阵进行分块处理，相比文献[12]，其非对角块矩阵元素减少，进一步降低串行计算量。

2 2级3阶Radau II A方法简介

电力系统电磁暂态过程通常可由一组微分方程来描述

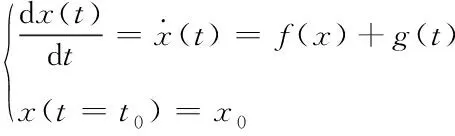
(1)

式中，x∈Rm×1，为电力系统状态变量的集合，g(t)仅与时间变量有关，t0为积分起始时刻，x0为起始时刻电力系统状态变量的初值。

2级3阶Radau II A法属于多级隐式Runge-Kunttu(RK)系列方法。其积分格式为

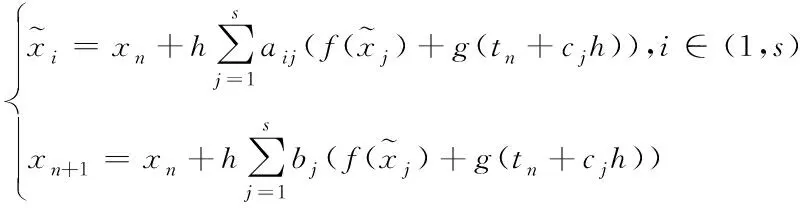
(2)

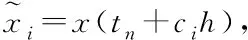
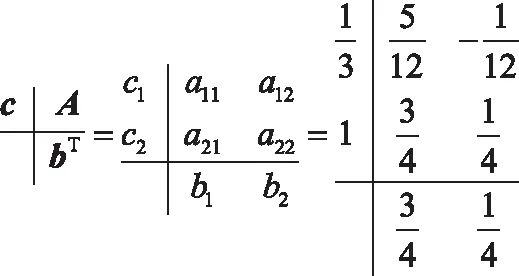
(3)

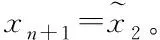
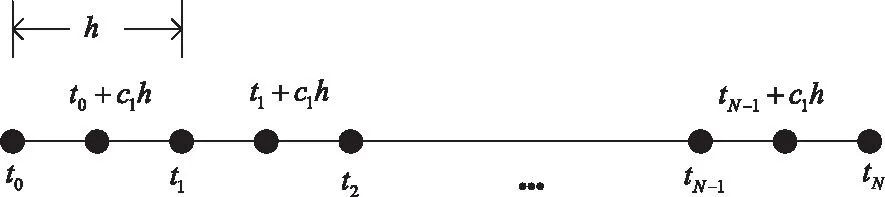
图1 时间网格点图

利用式(2)对式(1)在图1所示的N个网格点上进行连续离散，可得：

(H⊗Im)X=(B⊗Im)F(X)+(B⊗Im)G(t)+Const(t0)

(4)

式中

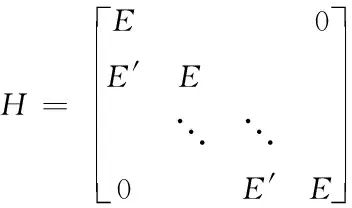
(5)

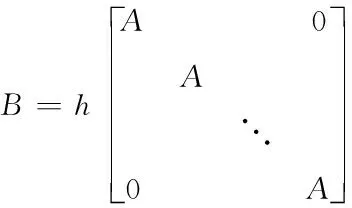
(6)

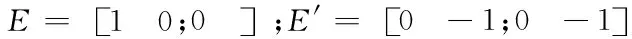
(7)

(8)

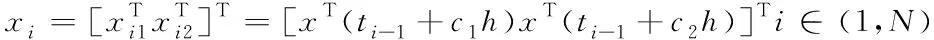
(9)

F(X)=[fT(x1)fT(x2)…fT(xN)]Ti∈(1，N)

(10)

G(t)=[gT(t1)gT(t2)…gT(tN)]Ti∈(1，N)

(11)

g(ti)=[gT(ti-1+c1h)gT(ti-1+c2h)]Ti∈(1，N)

(12)

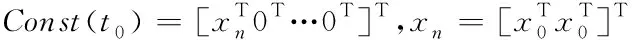
(13)

Im为m维单位矩阵。当式(1)描述为非线性初值问题时，利用严格的牛顿法对式(4)进行求解可得

-JΔX=ΔF

(14)

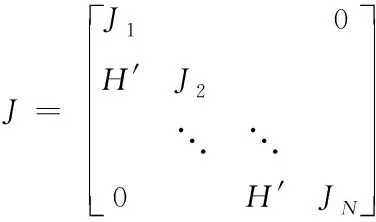
(15)

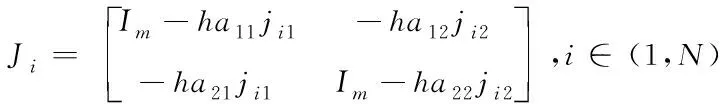
(16)

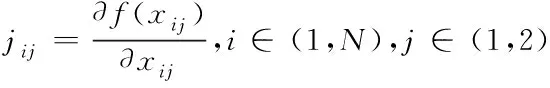
(17)

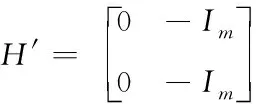
(18)

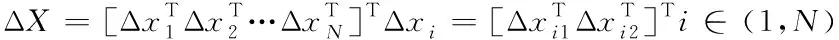
(19)

ΔF=(H⊗Im)X-(B⊗Im)F(X)-

(B⊗Im)G(t)-Const(t0)

(20)

令

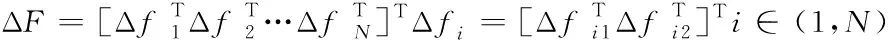
(21)

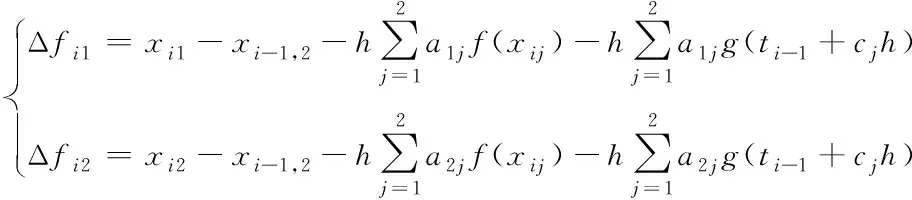
i∈(1，N)

(22)

其中：x0，2=x0

3 基于Sherman-Morrison公式的电磁暂态并行计算

经典的Sherman-Morrison公式可描述如下

(23)

式中：A0∈Rn×n；α，β∈Rn×1。对经典的Sherman-Morrison公式进行推广，表达式如下

(24)

式中：αk，βk∈Rn×1，k∈(1，n)，且

P=[pk]，pk∈Rn×1，k∈(1，n)

(25)

Q=[qk]，qk∈Rn×1，k∈(1，n)

(26)

R=diag(rk)，k∈(1，n)

(27)

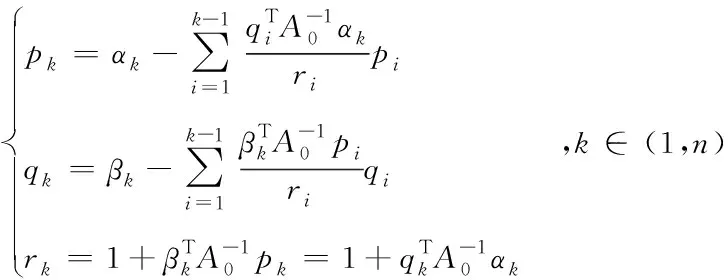
(28)

对于式(14)的求解，将从并行的途径获得加速比。由式(15)可见，J由对角矩阵和一个高度稀疏的常系数矩阵构成，因此可以巧妙地结合Sherman-Morrison公式求逆。

再观察式(28)，每一个pk，k∈(1，n)都由前k-1个pi，i∈(1，k-1)线性递推得到，当并行度越高，即n值越大，对式(28)的求解仍然具有一定的计算量，为了在保证并行度的同时，减少计算项，先对式(15)进行分块处理。

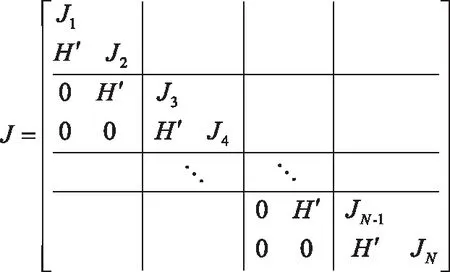
(29)

(30)

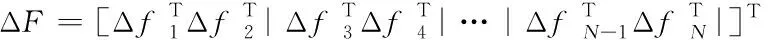
(31)

令

将式(14)变换得

-(Jd+ΔJ)ΔX=ΔF

(32)

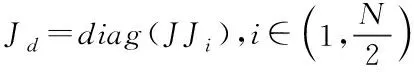
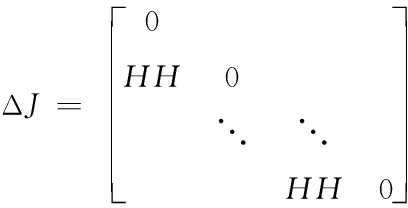
(33)

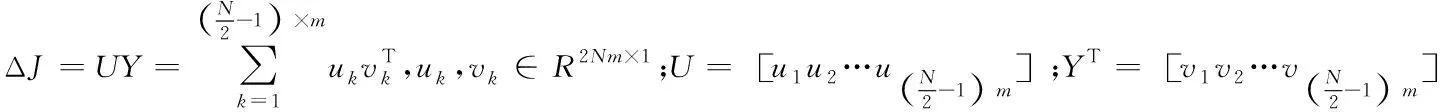
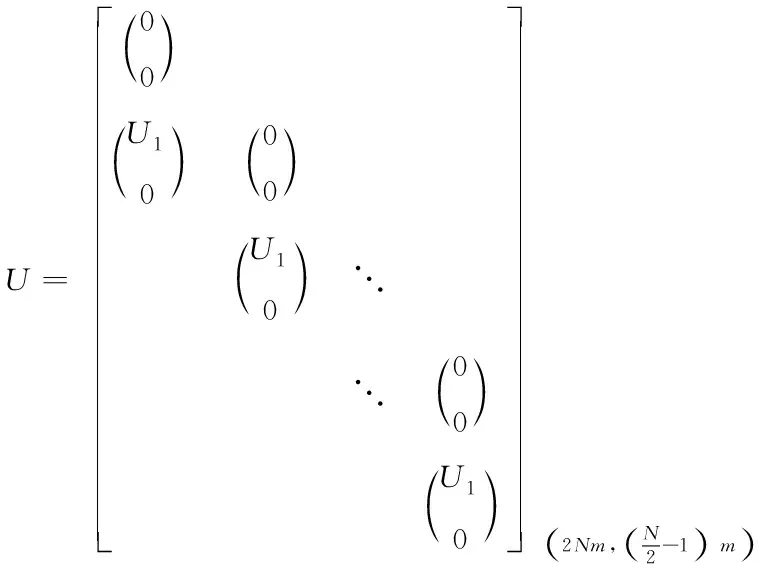
(34)

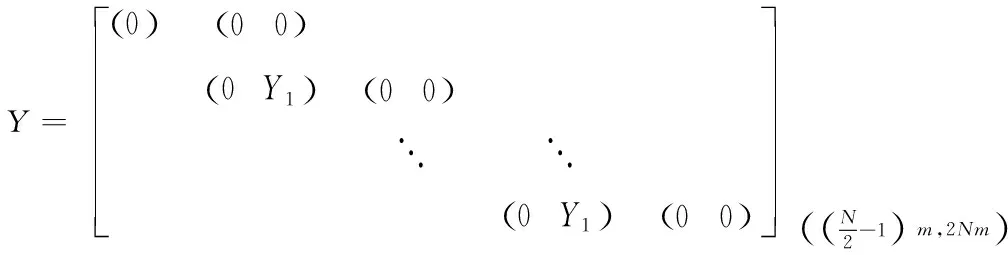
(35)

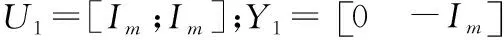
利用扩展的Sherman-Morrison公式求解式(32)，可得

(36)

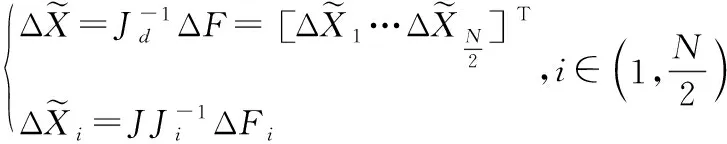
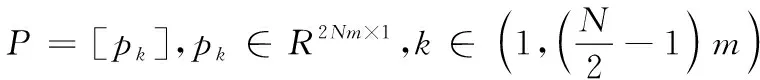
(37)

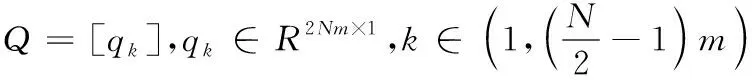
(38)

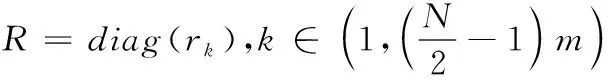
(39)

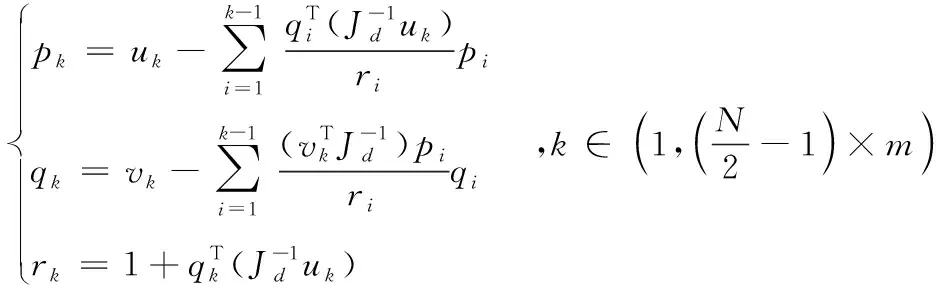
(40)

对式(36)的求解，可以得到以下结论：

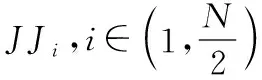
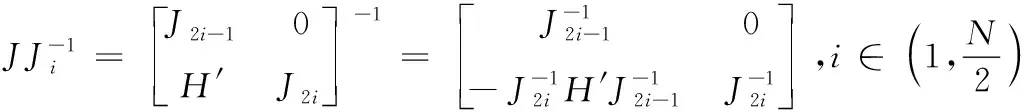
(41)

由式(41)可知，对于JJi的求逆计算转换为了对Ji，i∈(1，N)的求逆计算，并且彼此解耦，没有增加矩阵求逆的计算量。

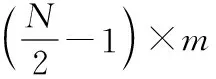
所提算法的计算步骤大致可以概括如下：

1)利用Radau II A法在N个时间点上连续离散，设置收敛精度为ε，并带入初值，严格牛顿法求解非线性方程组，得到式(14)；

2)对式(14)中形成的大雅可比矩阵进行分块处理，得到式(29)，式(30)以及式(31)；

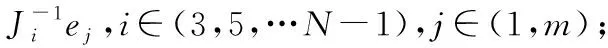
6)利用式(36)求解出ΔX，判断收敛性，若收敛则进行下一个时间网格点的计算，若不收敛；利用ΔX对X进行更新，转至步骤(3)进行迭代计算；

若式(1)描述为线性时变微分方程时，即

f(x)=Utx

(42)

式中，Ut为时变矩阵。

将式(42)带入式(4)，并整理合并得：

JX=C

(43)

式中：

(44)

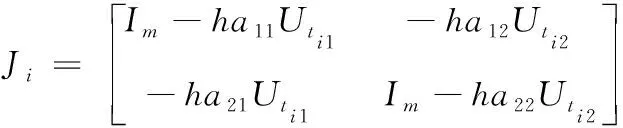
(45)

其中：Utij=U(ti-1+cjh)，i∈(1，N)，j∈(1，2)

C=(B⊗Im)G(t)+Const(t0)

(46)

按照非线性部分算法，将J分块后分解为Jd+ΔJ，利用Sherman-Morrison公式求解，后文不再赘述。

4 算例仿真

由于本部分两个算例均无法求出解析解，因此其仿真结果将会和小步长隐式梯形法仿真结果做对比。并且定义小步长隐式梯形法与本文算法的仿真时间之比为加速比k1，串行的大步长Rudau II A法与本文算法的仿真时间之比为k2，小步长和大步长在具体算例里都给出了定义。由于本文算法和串行Radau II A采用的步长和离散方法均是一致的，其仿真结果精度一致，因此只给出本文算法仿真结果图。两个算例的仿真均有16个计算单元参与并行计算。

4.1 输电线路连接非线性负载系统仿真

图2为输电线路连接非线性负载系统图。

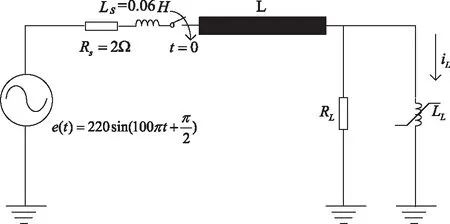
图2 输电线路连接非线性负载系统图

该系统的基本参数已在图2中标出。其中，输电线路L长为100km，其单位长度电阻，电感，对地电容为

R0=0.07Ω/km

L0=2.08×10-3H/km

C0=12×10-9F/km

(47)

和输电线路相连的负载由定电阻RL和非线性电感LL组合表示。LL中的非线性关系表示为：φ=atanhbiL。a=8.40×102V·s，b=5.95×10-3A-1。

输电线路由π型等值电路建模。将输电线路L分成M段，每段由图3所示线路表示。

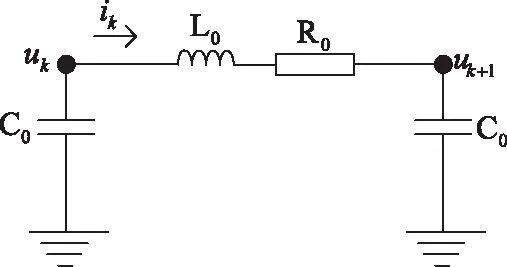
图3 π型等值电路图

其数学模型表示如下

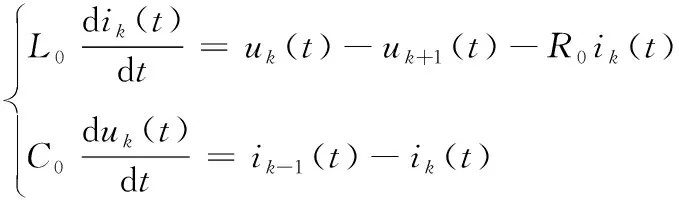
(48)

补充输电线路L的首端尾端约束方程如下

(49)

联立式(48)和式(49)，总的仿真时长为0.004秒。将输电线路分为30段，收敛精度设置为10-4。整理可得式(1)表达式。其中x∈R63×1。利用隐式梯形法对本算例进行离散仿真，其仿真步长为10-6秒，后文称为小步长；利用Radau II A法串行仿真；利用本文算法进行仿真，由于Radau II A法为多级方法，因此可以取大步长，将大步长取为隐式梯形法小步长的2s倍，因此本文将步长取为4×10-6秒，后文称为大步长。

图4给出了输电线路首端末端电压曲线，图五给出了与隐式梯形算法的误差图。由图5可见，即使采用了大步长仿真，其仿真结果依然保持了一定的精度。

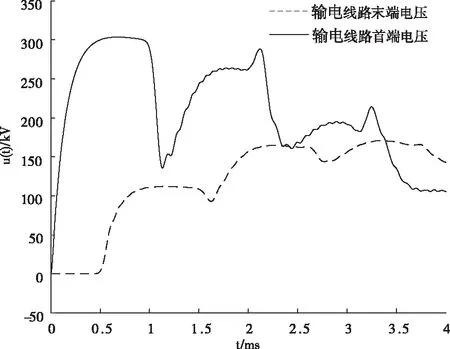
图4 输电线路电压曲线图

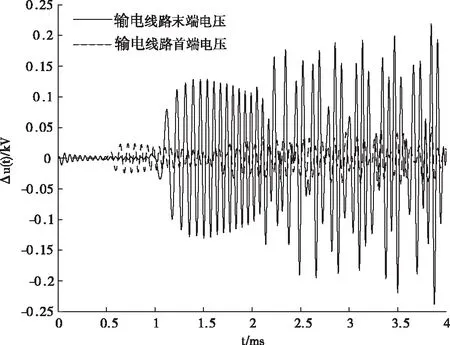
图5 仿真结果误差图

利用隐式梯形法小步长仿真，其仿真时间为7.23秒，利用Radau II A法大步长串行仿真，其仿真时间为7.56秒。每个时间步长内两次迭代即完成收敛。

加速比由表1给出。

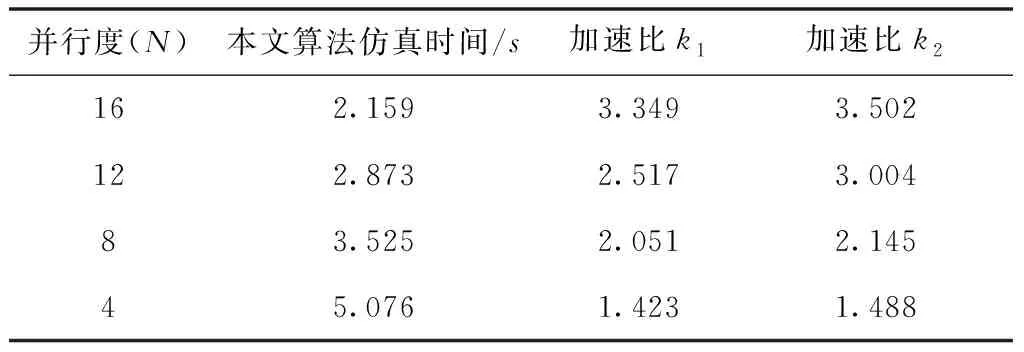
表1 加速比

由表1可以看出，采用RadauIIA法大步长仿真的时间和隐式梯形法小步长仿真的时间大致相等，这是由于引入内点增加计算量的原因。因此若直接将RadauIIA法运用到电磁暂态计算中，将不会产生明显的加速效果。所提算法在N个时间点上实现了并行求逆，并且基于非对角块矩阵高度稀疏和常系数的特点，使得串行过程只涉及简单的向量计算，并且分块处理后相比于分块前减少一半计算量，进一步地加快了所提算法的计算速度。且当并行度越高所获得的加速比也越高。

4.2 VFTO算例仿真

隔离开关投切空载短母线时会产生特快速暂态过电压(VFTO)，会对与其相连的电气设备造成损坏，因此对VFTO的快速仿真也显得尤其重要。图6为产生VFTO的系统图。

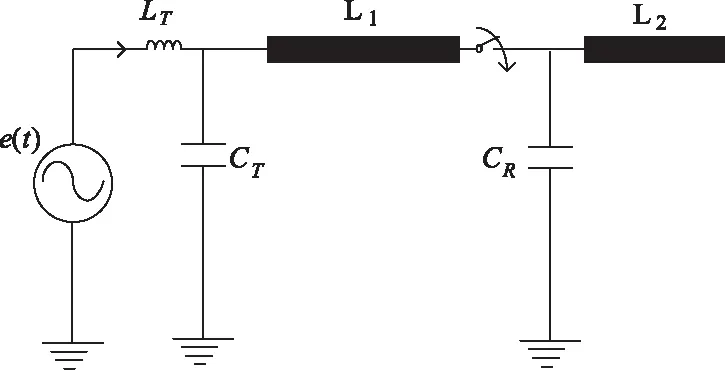
图6 VFTO系统图

L1和L2为短母线，L1长10米，L2长3.5米，由隔离开关连接，隔离开关对地电容由CR表示，CR=240pF。而变压器则由LT和CT组合表示，LT=20mH，CT=3000pF。考虑最严重的VFTO，即短母线上的残余电压与电源电压差高达两倍.p.u(即电源侧取1.0倍.p.u，短母线上取-1.0倍.p.u)。当开关合闸时，其变换过程由时变电阻Rt来表示，其数学表达式为

Rt=R1e-t/τ1+R2e-t/τ2

(50)

式中：R1=1012Ω，R2=0.5Ω，τ1=1ns，τ2=1μs。本算例里将短母线L1分为20段，将短母线L2分为7段，单位长度电感L0=2.5×10-7H/m，单位长度电容C0=4.45×10-11F/m。采用算例1用的π型等值电路建模的方法对输电线路L1，L2建模。得到其数学模型为

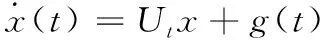
(51)

式中：Ut∈R57×57，为时变矩阵。仿真总时长为1.2微秒，利用隐式梯形法对式(51)进行离散仿真，步长取为0.1ns(小步长)；RadauIIA法串行仿真，和算例一同样的原理，将步长取为2s倍隐式梯形法仿真步长，即0.4ns(大步长)；本文算法进行大步长仿真。图7给出了输电线路L2末端电压波形以及与隐式梯形法仿真结果的误差曲线图，由图可见，RadauIIA法具有大步长高精度仿真的优势。

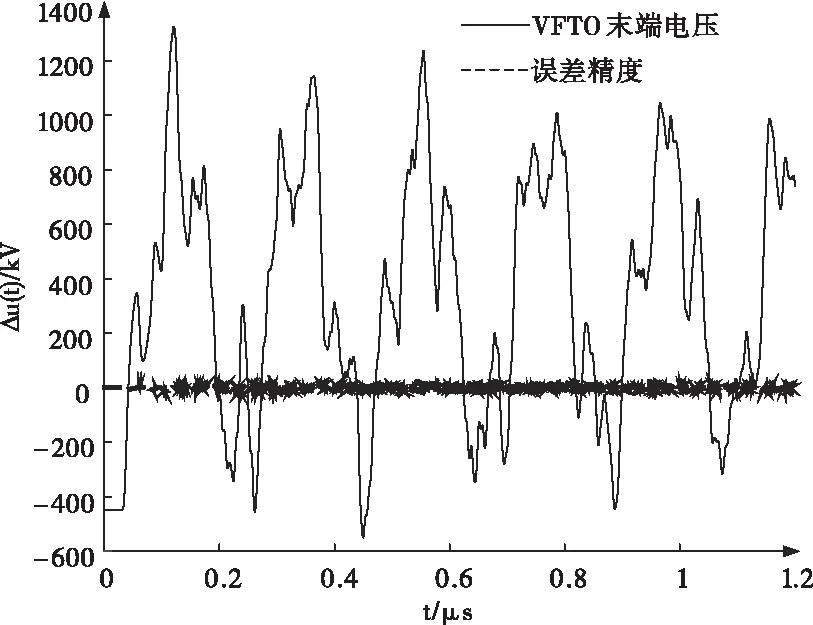
图7 VFTO仿真结果和误差图

加速比如下表可见，k1，k2定义和算例1一致。隐式梯形法小步长仿真时间为5.871秒，RadauIIA法大步长串行仿真时间为6.023秒。

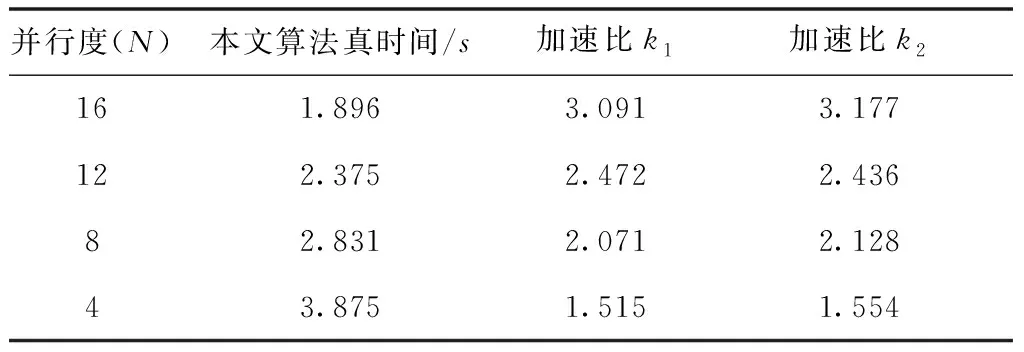
表2 加速比

和算例1同样的分析方法，所提算法利用Sherman-Morrison公式并行求解对角块矩阵，分块处理减少了非对角块元素，进一步降低计算量，并获得了可观加速比。

5 总结

所提算法将RadauIIA法和Sherman-Morrison公式结合起来，提出了一类基于RadauIIA法的电磁暂态并行计算方法。并通过两个经典算例在精度和加速比两个方面的对比分析中得出了以下结论：

1)所提算法均是在严格牛顿迭代法上形成的，因此具有严格牛顿法的收敛性。

2)RadauIIA法因引入内点，具有高阶计算精度，因此可采用较隐式梯形法更大步长仿真。

3)通过对高维雅克比矩阵进行分块处理，利用Sherman-Morrison公式并行求逆，获得了较好的加速比，且并行度越高，加速比越大。

因此，本文算法可以提高基于2级3阶RadauIIA法的电磁暂态计算速度。