基于能源多类型网络构建低碳能源社区

孟 良，周 文，李 扬，张照彦

(1. 国网河北省电力有限公司电力科学研究院，河北 石家庄 050021；2. 国网雄安思极数字科技有限公司，河北 雄安 071700；3. 河北大学电子信息工程学院，河北 保定 071000)

1 引言

城市地区由于其日益增长和不断变化的能源需求，能源网络和环境影响越来越大。据国际能源机构称，在全球范围内，城市地区占一次能源使用的70%以上，占温室气体排放的60%以上，并随着城市化率的提高而增加[1-2]。与此同时，在全球范围内许多国家和组织也观察到在评估碳排放方面的总体进展，这将转化为鼓励使用可再生能源和惩罚化石燃料能源的政策[3]。低碳区和可持续发展的概念引起了许多学者的广泛兴趣，学者们探讨相关技术和提出相关政策。

文献[4]对可用于模拟区域一次能源系统之间复杂的相互作用和能源需求的建模方法进行了全面研究，从不同的角度和规模来解决设计问题。文献[5]从经济、能源、环境和社会的角度，提出了七个指标来评价低碳区的性能。文献[6]从政策方面以上海为例，研究城市低碳转型和政策演变的机理，其研究促进了中央和地方政府之间的合作，提出了将自上而下的设计与自下而上的创新相结合的混合方法。

微电网也常常被视为解决城市化挑战和促进实现低碳区的有效办法，其是由分布式电源(包括传统和可再生能源)、负荷和储能系统组成的小规模能源网络[7-9]。文献[10]利用微电网固有的可控和灵活的性质，对微电网优化控制，以最大限度地实现当地可再生发电的自我消费，减少客户的能源费用；在电网故障情况下，以孤岛模式运作，提高供电服务的可靠性。

多联产即同时产生多个能量，是以最有效的方式满足一个地区在电力、供暖和供冷等能源需求[11-12]。研究表明从环境的角度分析，多联产系统是有很意义的，其减少了等效CO2的排放，以及确保了更高的功能服务可靠性，同时减少了能源成本。多联产系统如热电联产和三联产系统，有助于减少最终用户和地区的一次能源消耗。由于多类能源系统之间相互耦合以及满足用户的需求，导致多联产系统的设计和管理复杂。目前可以利用数值建模、仿真技术和优化理论，设计和管理多联产系统。文献[13]通过求解混合整数线性规划(MILP)问题以解决城市地区的最优调度问题，其目的是在网络连接和孤岛模式下使成本最小化。文献[14]提出了一种多目标方法来优化多能源网络，其中电气、加热和热水需求相对于总成本和一次能源输入得到最优满足。文献[15]考虑不确定的规划阶段在一个电采暖多联产装置，通过在最坏情况下模拟装置总成本来考虑不确定性。

本文以最佳规划和设计一个区域能源社区，通过建模的方式建立一个能源枢纽集群，包括多类能源，以最佳方式满足能源需求(电力、供暖和制冷电力需求)。该模型的目标是对局部区域采用整体设计方法，将其配置为当地能源社区，确定能源系统(分布式发电、可再生能源、热能和电能储存)和能源网络基础设施(电力、地区供热和供冷网络)的最佳组合，以满足最终用户的需求。本文提出的模型能够对不同能源网络之间的相互作用和协同作用进行建模。将该区域的碳排放引入到约束条件中，通过epsilon约束方法将一次能源消耗限制在预定水平内。这种方法被用来强调在基于纯经济优化的最优解和考虑碳排放的替代方案之间进行某种设计权衡的必要性。基于某区域的五个住宅小区的真实数据，验证所提模型和方法的有效性。

2 社区能源模型

将社区建模为一组空间错位的住宅站点，分别代表不同的最终用户，每个站点有本身的能源需求(电力，冷热负荷)。根据能源枢纽建模策略，每个站点遵循相同的参考布局和能源部署。社区能源模型有以下特征：

1)不同地点可以同时安装电能储能装置和储热装置；

2) 光伏发电装置不仅可以集中布置，而且还可以分布在每个站点；

3) 能源网路中的不同节点除可以交换热能和冷能外，还可以交换电能，多余的电能除了回馈电网外，还可以在区域用户之间共享剩余的电能；

4) 每个节点本身就是一个多能网络：目前有电力、热能和冷能网络。

图1为低碳社区群能源结构框图，每个社区即为一个站点，有自身的电力、热能和冷能需求，由天然气发电机(CHP)供电的热电联产系统、燃气锅炉(BO)、电制冷机组(EC)和吸热式制冷机组(AC)、以及电池储能(EES)和冷热储存装置(ETS)构成社区能源模型。社区能源模型将不同站点连接起来，以便通过物理能源网络交换能量，如图2所示，各个站点之间可以交换冷热电能量。

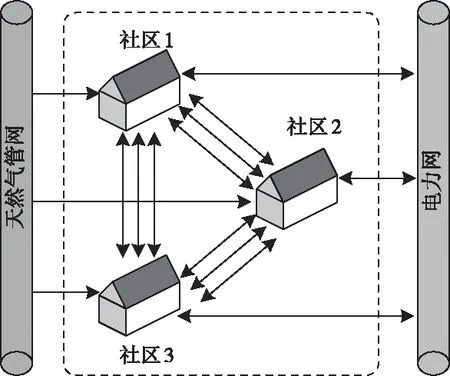
图2 社区群内部能量流示意图

区域优化规划选择在每个站点配置最佳能源系统组合，最优先满足区域内用户的能源需求。通过选择每个站点要安装的能源类型及其相应的容量，会有不同的设计方案。例如：一个能源社区可能完全依赖电网来维持其能源需求；而另一个能源社区可能需要安装一些分布式发电系统，将所有能源生产集中在少数站点，从而需要一个地区供冷、供热网络。最优设计是根据经济和环境目标确定，以及考虑到新能源系统投资和在运行期间内维持系统运行的相关成本。

3 混合整数线性规划模型

混合整数线性规划(MILP)建模是通过确定一组二进制变量来选择安装和运行不同能源类型的建模方法。仿真时间步长间隔为1小时，并且在方程式中由自变量h进行索引，该自变量h包含在仿真总时间段的集合T中。

各个站点内的不同装置由二进制变量Ycomp(szcomp，u)表示即称为存在变量，其中szcomp表示装置的容量，u是装置安装位置的索引。站点索引u或v包含在表示所有物理站点的集合U中。

为了对每个装置的运行状态建模，对该装置设置约束条件，判断装置在时间h内是否运行。由二进制变量Xcomp(szcomp，u，h)表示，该变量必须等于或小于存在变量Ycomp，因为如果存在变量Ycomp=0，将无法操作。提出每个装置在时间跨度h的约束条件

Xcomp(szcomp，u，h)≤Ycomp(szcomp，u)

∀h∈T，∀u∈U

(1)

只有当一个装置存在时，Ycomp变量设置为1，同样可以通过操作将Xcomp变量为设置为1。本文考虑以下装置：往复式燃气发动机(CHP)、天然气锅炉、吸热式制冷机组、电力制冷机组、(冷)热能储存、电力储存和光伏装置。

同样使用相同的二进制变量约束条件，给出两个不同站点之间物理连接存在的约束条件

Qconn(u，v，h)≤Capconn×Xconn(u，v，h)

∀h∈T，∀u，v∈U

(2)

Xconn(u，v，h)≤Yconn(u，v)

∀h∈T，∀u，v∈U

(3)

式中二进制变量Yconn(u，v，h)表示站点u和v之间存在连接；Xconn(u，v，h)表示时间跨度h内的运行状态；Qconn(u，v，h)是u和v在时间跨度h内交换的能量；Capconn是通过物理连接在时间跨度h内可以交换或传输的最大容量。

模型在AIMMS优化建模环境中构建，以CPLEX为求解器；优化问题计算不设置时间限制，只使用MIP最优容差，最优容差被设置为5%。

3.1 分布式能源系统和多联产模型

能源装置(CHP、BO、AC、EC、PV)通过设置生产效率(年平均效率)的恒定值和输出功率的上限和下限建模。

燃气轮发电机基本公式如下：

∀h∈T，∀u∈U

(4)

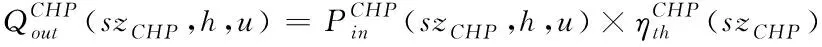
∀h∈T，∀u∈U

(5)

∀h∈T，∀u∈U

(6)

∀h∈T，∀u∈U

(7)

XCHP(szCHP，h，u) ≤YCHP(szCHP，u)

∀h∈T，∀u∈U

(8)

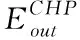
锅炉遵循类似的建模策略，其公式为

∀h∈T，∀u∈U

(9)

∀h∈T，∀u∈U

(10)

∀h∈T，∀u∈U

(11)

XBO(szBO，h，u)≤YBO(szBO，u)

∀h∈T，∀u∈U

(12)

对于吸热式制冷机组，其公式为：

∀h∈T，∀u∈U

(13)

∀h∈T，∀u∈U

(14)

∀h∈T，∀u∈U

(15)

XAC(szAC，h，u)≤YAC(szAC，u)

∀h∈T，∀u∈U

(16)

对于电动制冷机组，其公式为

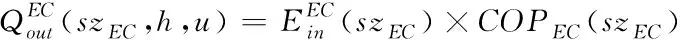
∀h∈T，∀u∈U

(17)

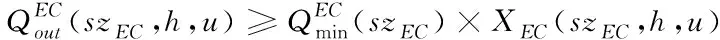
∀h∈T，∀u∈U

(18)

∀h∈T，∀u∈U

(19)

XEC(szEC，h，u)≤YEC(szEC，u) ∀h∈T，∀u∈U

(20)

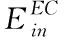
对于光伏系统，产生的电功率是电池板占据的总面积(SPV)和辐射值(IRR)的函数，辐射值(IRR)被定义为每小时辐射值，电功率公式如下

∀h∈T，∀u∈U

(21)

式中ηPV光伏电站的年平均效率。

3.2 储热和储电模型

热电储能按照以下标准建模：

1)储能模型必须验证在每个时间跨度内请求存储的能量不超过当前存储容量；

2)模型必须检测当前存储容量不超过存储的标称最大容量。

对于储热模型，按照标准化建模，可用以下方程表述：

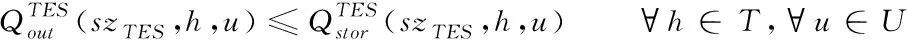
(22)

(23)

式(24)表示储热的能量平衡，当前时间跨度h的储热取决于前面时间跨度的输入和输出热量，如下所示

∀h∈T，∀u∈U

(24)

无论是充能/放能，充放效率被认为是恒定的。储热模型还包括一个约束条件，以避免储能在相同的时间内同时充能和放能，如下所示

X1TES(szTES，h，u)+X2TES(szTES，h，u)≤YTES(szTES，u)

∀h∈T，∀u∈U

(25)

式中X1TES和X2TES表示存储操作状态的二进制变量，X1是充能模式，X2是放能模式。

同样的建模方法也应用于电能存储，公式如下

∀h∈T，∀u∈U

(26)

∀h∈T，∀u∈U

(27)

∀h∈T，∀u∈U

(28)

X1EES(szEES，h，u)+X2EES(szEES，h，u)≤YEES(szEES，u)

∀h∈T，∀u∈U

(29)

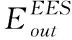
3.3 分布式能源网络模型

区域网络内不同站点之间的能量传输可以通过之间的基础设施网络实现，如地区供暖/供冷网以及电网。

对区域供冷网进行建模，式(30)表示利用热管在各站点之间交换的最大热功率：

(30)

式中ρ和cp是管道中工质的密度和比热，v是管道内工质流动的速度，Dpipes是管道的直径，ΔTpipes是管道两端的温差，n是连接站点的管道数。区域供热或供冷网的热损耗是通过站点之间的距离(即模型的输入)乘以热管(W/m)的线性热损耗计算得出。

关于各站点之间的电网，因为各场址之间的距离太短，因此可以忽略损失。

3.4 目标函数

模型中实现的目标函数是系统寿命期间的最小总成本。总成本包括投资成本、运营成本以及维护成本。

Ctot=Cinv+Cop+Cmain

(31)

投资成本Cinv考虑了购买装置和物理网络在站点之间交换能量的成本。投资成本按下列方程计算

Cinv=∑u∑comp∑szCcomp(szcomp)×Ycomp(szcomp，u)

×fcomp+∑conn∑u，v u≠vcconn×Dconn(u，v)

×Yconn(u，v)×fconn

(32)

式中Ccomp表示购买sz容量装置的成本，Ycomp表示存在；物理网络连接的成本是通过将以每米成本cconn表示的物理连接的特定成本乘以两个变量来估算的，两个变量分别为连接Yconn(u，v)的存在和两个站点u和v之间的距离(Dconn)。所有购买成本系数f即fcomp和fconn的计算要考虑利率因素和装置的预期寿命。

(33)

式中i为利率；n为装置预期寿命，单位为年。

运营成本Cop包括三部分：前两部分与锅炉和热电联产单位燃料消耗成本有关；最后一个要考虑购买的电能(Epur)和出售(Esold)的电能。经营成本的公式如下

(34)

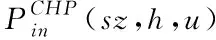
维护费用Cmain表示如下：

Cmain=∑u∑comp∑szcmcomp(szcomp)×Ycomp(szcomp，u)

+∑conn∑u，v u≠vcmconn×Dconn(u，v)×Yconn(u，v)

(35)

式中cmcomp(szcomp)每个装置的固定年度维护成本，以￥为单位；cmconn是物理连接的固定年度维护成本，以￥/m为单位。

3.5 能源消耗约束条件

低碳目标是通过遵循epsilon约束方法来实现的。为了减少与社区传统消费模式相比的一次能源消费总量，引入一项限制措施以作为比较基准。该约束条件考虑了满足电力、供暖和供冷需求所花费的一次能源，并引入一个减少因素即总体一次能源减少目标。约束条件如下为：

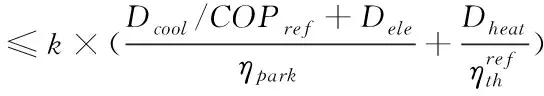
(36)

值得注意的是，根据约束条件，一次能源消耗可以通过引入多联产系统，如热电联产单元和可再生能源系统来实现，这些系统有助于增加微电网的发电量，从而减少从电网购买的电量，或在自产超过地区消费时增加向电网出售的电量。

4 测试案例分析

该模型用于研究位于广东某区域的能源社区，对5座住宅区进行了调查，并利用其冷量需求的实际数据对最终客户的需求进行建模。研究的测试案例只考虑电量和冷量需求。

4.1 客户需求

分析考虑了5座住宅区的实际情况，其代表五个空间错位的站点，每个站点目前都安装电制冷机组的冷却系统提供供冷服务。这五个站点都连接于公共电网，在目前的研究中电网作为主要网络。各站点2019年7月份供冷用电需求见图3。

图3 社区电量月负荷和冷量月负荷

冷负荷数据由安装在每个制冷站的实时能量监测系统收集。图4是社区1站点的冷量日负荷和电量日负荷，图5是社区1站点的冷量周负荷和电量周负荷。同时在优化时考虑了连接站点的物理设施的距离，如表1所示。

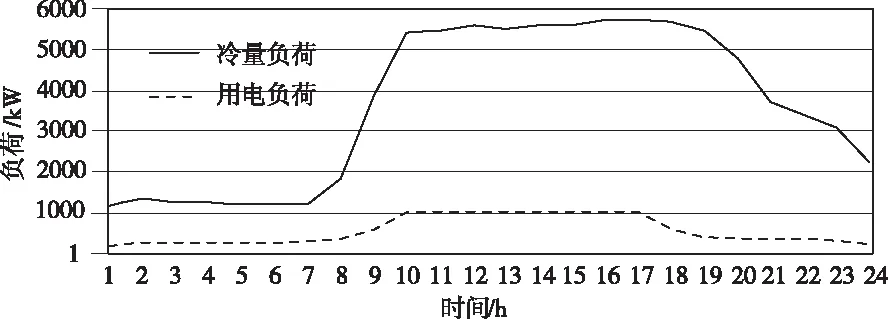
图4 社区1冷量和用电日负荷曲线

图5 社区1冷量和用电周负荷曲线

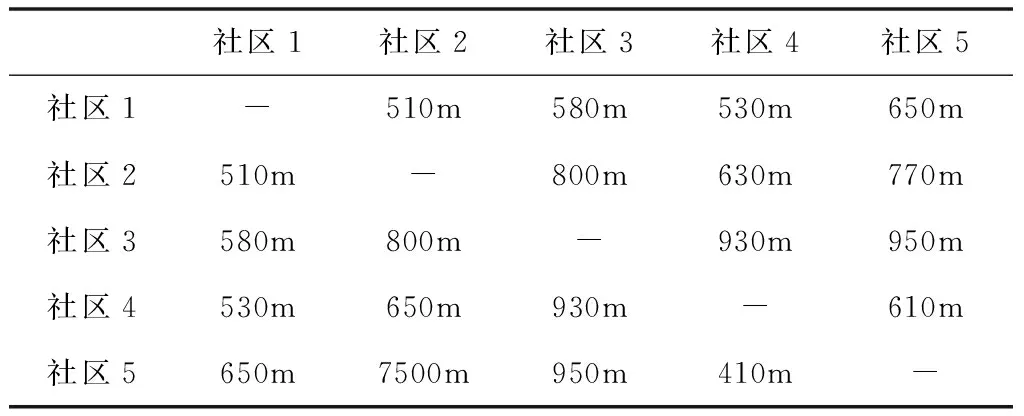
表1 五个社区的相对距离

4.2 方案

本文两种不同的方案：

1) 第一种方案仅从经济角度确定最佳解决方案，对电网运行或总体排放没有特别的限制；

2) 第二种是使用所述的额外限制条件以限制第一种方案的一次能源消费总量。

第一种方案是对该区域进行纯粹的技术经济优化，而第二种方案是在社区一次能源消费减少目标的约束下提供最优的技术经济解决方案。一次能源使用量减少是能源规划者优先考虑的目标之一，在本文中第二种方案减少一次能源消费的10%为目标。两种方案都考虑从电网购买和出售的电量，购买和出售电量的价格不同，前者高于后者。

4.3 案例分析

4.3.1 方案1分析

方案1以纯经济驱动优化为目标，而方案2以减少一次能源消费的10%为目标。方案1的最优解需要将五个站点中的四个与区域内供冷网络连接，并根据当前的配置，重新设置电制冷机组的大小。区域供冷网络解决方案的优点主要与电制冷机组的投资成本低有关，可以部分抵消区域供冷网络的成本。事实上，在五个分离站点的配置中，电制冷机组的规模分别满足每个站点的最高冷负荷需求；而在区域供冷网络中五个站点的冷负荷需求可以看作是一个独特的聚集需求，装机容量的裕量不用太大，满足聚集需求即可。图6是实际5个社区站点的用冷负荷，图7是采用方案1优化之后的5个社区站点的冷负荷曲线。

图6 社区的实际用冷周负荷曲线

图7 方案1中社区用冷周负荷曲线

目前5个社区地点都有供冷能力，从图6可以看出，为满足冷负荷的峰值需求，总共需要25.5MW的供冷量。

通过方案1的优化算法计算之后，从图7中可以得出在满足5个社区站点相同冷负荷需求的情况下，需要总的供冷能力为17.1MW的电制冷机组来维持即可，这意味着电制冷机组的配置容量减少了33%，而减少的33%供冷量是通过利用区域供冷网络和储冷系统来实现，表2为通过方案1优化计算后得出的能源装置配置表。

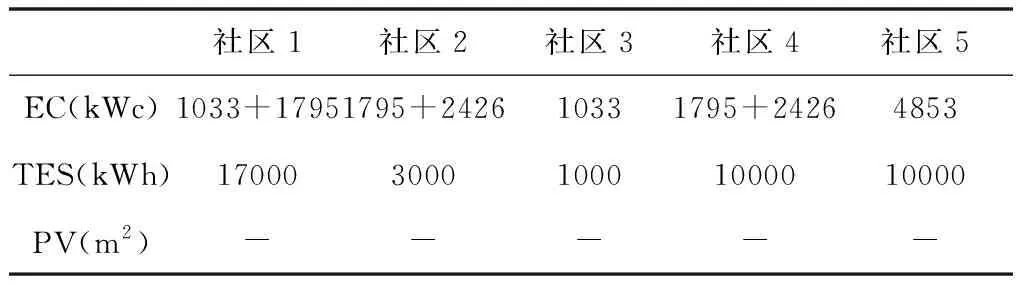
表2 方案1优化计算后的能源装置配置表

需要说明的是：最优解决方案1是对站点2产生的冷功率进行调峰，而需求峰值由站点5的产生的冷功率来满足，并由区域冷却网络提供。相对于实际配置(图6)，在最优解中由于存在供冷网络，安装在站点5的供冷系统周末也运行，以补偿其公站点，主要是站点2和站点4的冷功率峰值。图7表明在最优解中，站点4生成的冷功率也在峰值时被消去，站点5中产生了附加的峰值功率。这一解决方案增加了该区域供冷负荷系统的可靠性，因为在一些电制冷机组发生故障或处于维修状态时，每个社区站点所需的冷功率都可以依靠其公站点供应。

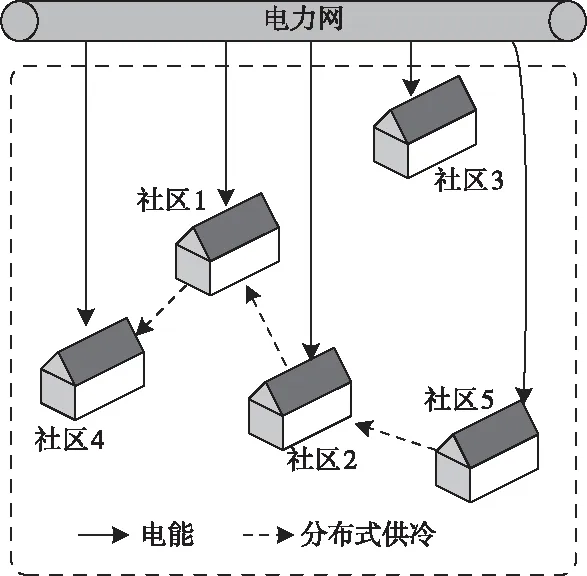
图8 方案1的区域供冷网络最优拓扑结构

为了更好地理解优化算法得到的区域冷却网络的最优拓扑结构，图8进一步表明了该算法在各个站点之间建立的物理连接。图8中的连接线表示区域供冷网络中两个站点之间的物理连接，而箭头的方向表示冷量流动的方向。冷量需求较低的站点5通过站点2将产生的所有剩余冷量输送到区域供冷网络中：即站点5产生的冷量通过供冷网络首先输送到站点2中，但是不一定被消耗在站点2，而是可以发送到站点1或站点4。

4.3.2 方案2分析

方案2的目的是促进该地区的低碳排放，即减少总的一次能源消耗，如上文所述，方案2中将一次能源消耗减低10%为目标。根据式(36)给出的约束条件，将参数k设置为0.9，即方案2的最优设计与基准线相比，一次能源消耗减少10%。

基于方案1中的最优解配置中包括分布式冷能存储和区域供冷网络，其连接布局如图9所示。

相对于方案1，在方案2中的每个社区站点都安装了一个光伏电站。根据最优解的完整配置，即所安装的装置及其相应的容量，如表3所示。

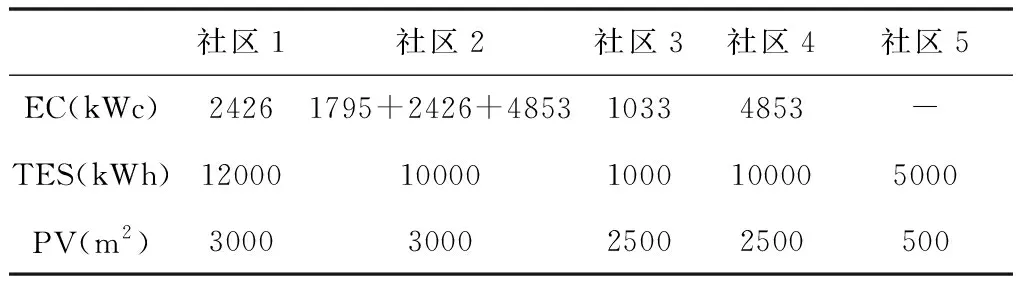
表3 方案2优化计算后的能源装置配置表

主要的制冷能力集中在站点1、站点2和站点4，而站点5除了5000kWh的冷储能外，没有安装电制冷机组，其所需的冷负荷由区域供冷网络和储冷装置提供。

图10和图11分别按小时列出了站点2的冷负荷和用电功率平衡曲线。从图10中可以看到，站点2生产的冷量大部分时间超过了自身的冷量需求，多余的冷量通过区域供冷网络发送到站点4，或储存到站点2中储冷装置中。从图11中可以看出光伏电站的发电量不足以满足站点2的电量需求，因此电量大部分都是从售电公司购买。

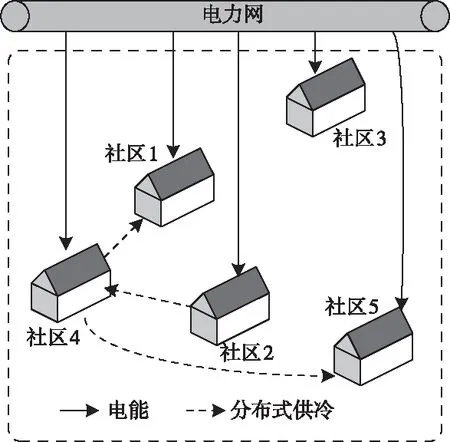
图9 方案2分布式网路连接配置

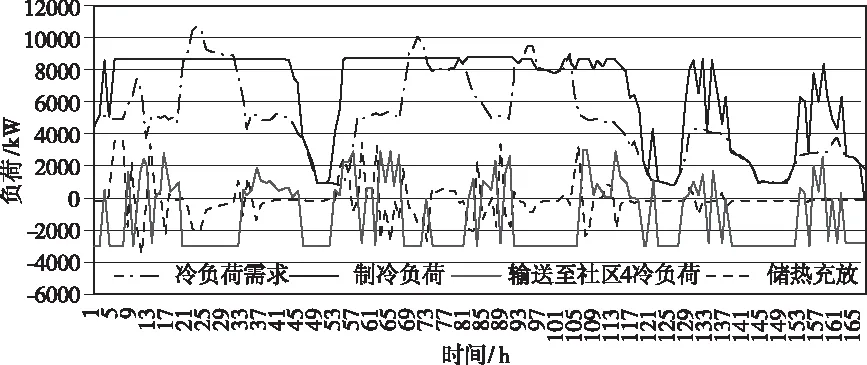
图10 方案2中社区站点2冷负荷平衡曲线

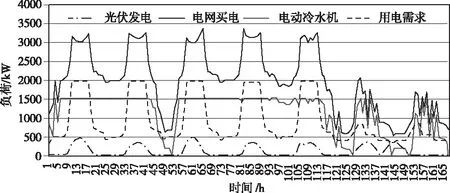
图11 方案2中社区站点2用电负荷平衡曲线

综上两种方案在优化计算后装置配置中都有共同之处，即安装区域供冷网络和储冷装置。所以在系统运行期间内，由于安装的总制冷容量较低，所以在投资和维护成本方面实现的成本节省可以补偿这两项资产的初始投资。

“低碳”能源社区旨在减少一次能源的总体消耗，其能源消耗的减少可以通过增加可再生能源来实现。表4显示当地能源社区依赖于电网的小时百分比，再除以五个站点，可以得出一次能源削减目标越大，其在当地能源社区内的分布式发电系统的份额就越大。此外分布式能源系统、能源储存和能源网络的整合也提高了该区域的能源供应抗扰动能力，即如果一些制冷机组发生故障或维修，本站点都可以依赖其他站点的能源系统。在成本费用方面，方案 1和方案2的成本仅相差1%，这意味着光伏电站、冷量储存的“低碳解决方案”(方案2)非常接近“纯经济”解决方案(方案1)。

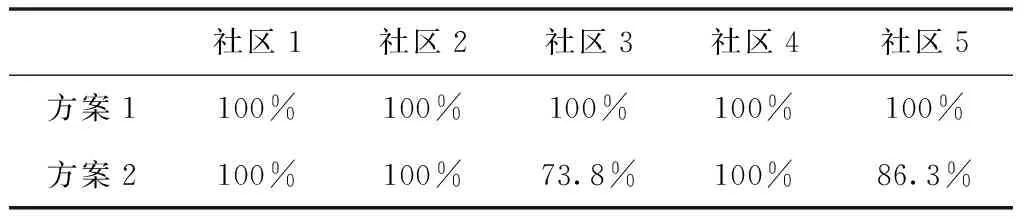
表4 两种方案能源网络使用对比

5 结论

本文提出了一种新的能源系统和网络优化规划模型，旨在降低能源社区的碳排放。将能源社区建模为一个能源枢纽网络，由空间错位的站点或社区组成的集群，每个站点都有维持自身需求的电力、热能和冷能，其可以由一个或多个能源转换和储能系统提供。本优化算法在原能源供应的基础上，实行低碳限制，以强制减少能源社区的总体一次能源消耗。该方法用于研究某区域内五个空间错位站点的能源最佳规划问题，每个站点都由一个配备电制冷机组提供冷量服务，利用真实数据对站点的电量和冷能需求进行建模，并提出了两种方案。第一个方案“纯经济”优化，而第二个方案则增加了将一次能源消费总量减少10%低碳限制。方案1通过安装分布式冷能储存和重新配置电制冷机组的容量并通过供冷网络连接各个站点，可将峰值冷功率容量降低33%。从经济层面可以得出，方案2与方案1的成本仅相差1%，两者基本是等价的，所以在满足经济性的前提下又实现了一次能源消费总量减少10%的目的。最终结果表明，通过广泛使用可再生能源、能源储存，通过利用不同能源网络之间的协同作用，可以实现“低碳能源社区”。