新能源、化石能源和高科技公司股价动态相依结构研究
杜子平, 孙瑞泽
(1.天津科技大学 经济与管理学院,天津 300222; 2.南方科技大学 商学院,广东 深圳 518055)
0 引言
我国经济的高速增长离不开化石能源消耗量的急剧增加。由于资源禀赋特点,化石能源在未来相当长的一段时间内仍将是我国的基础能源[1]。然而,对化石能源的依赖存在很多弊端。人类活动造成的温室气体排放主要源自化石能源的消费,进而引发的全球气温升高对人类的生存和发展提出了一系列严峻挑战;而作为人口稠密的发展中国家,中国更是首当其冲——无论在控温的经济代价还是气温升高带来的危害方面,中国均高于全球平均水平[2]。为对内兼顾经济发展与生态环境保护、对外树立负责任的大国形象,发展新能源是必由之路。在用新能源置换传统能源的过程中,科技水平起着关键作用。国务院印发的《能源发展战略行动计划2014~2020年》指出,推进能源科技创新是建设能源强国五大主要任务之一;国家能源局在“十四五”规划编制工作中强调,要打造以技术进步为核心、具有自主知识产权的新能源产业体系。
以科技为核心的新能源发展战略的合理性可以从资产收益率相依结构研究的视角窥见一斑。自Henriques和Sadorsky[3]开创性的工作以来,高科技和新能源公司股价联动性受到越来越多的关注。Henriques和Sadorsky[3]采用VAR模型和格兰杰因果检验研究了新能源公司股价、高科技公司股价、油价和利率间的关系,研究表明高科技公司股价对新能源公司股价的影响比油价更显著。他们指出,在高科技产业之外,新能源产业是重要的科技创新输出者,因此投资者将两个产业视为同质的整体。Sadorsky[4]通过多元GRACH模型考察了新能源公司股价、高科技公司股价和油价三者之间的条件相依和波动溢出效应,发现新能源和高科技公司股价间相依关系的强度高于新能源公司股价和油价间相依关系的强度,进而指出新能源与高科技公司的商业模式具有很高的相似性。Managi和Okimoto[5]利用马尔可夫状态转换VAR模型的研究发现,在2007年的一个状态改变后新能源公司股价和高科技公司股价联动更加密切,他们认为这是由于两行业面临相似的补贴政策。在常用的VAR模型和GARCH模型之外,Bondia et al.[6]采用门限协整模型、Inchauspe et al.[7]采用时变多因子资产定价模型、Zhang和Du[8]采用TVP-SV-VAR模型的研究均支持了Henriques和Sadorsky[3]的结论。在另一方面,当前对中国新能源和高科技公司股价相依关系的研究较少,且尚未达成共识。秦天程[9]指出,国内新能源公司股价对高科技公司股价变动不敏感,他认为这是由于国内新能源公司科技含量不足,投资者更加关注的是新能源这一概念而非其背后的技术优势;相反的是,Zhang和Du[8]的研究发现中国的新能源和高科技公司股价是密切相关的。为对新能源行业与高科技行业之间相依关系的密切程度得出结论,需要选择合理的基准进行比较。早期研究多采用化石能源价格和新能源公司股价之间的相依关系作为基准,而Zhang和Du[8]首先将新能源、化石能源和高科技公司股价纳入同一分析框架,他们指出:新能源和高科技公司所需求的资源有诸多共同点,因此新能源和高科技产业的同质性要大于新能源和化石能源即能源产业内部的同质性。
从文献回顾可以看出,高科技和新能源公司股价相依性的强度间接反映投资者是否将新能源产业视为重要的科技创新提供者,而深入分析三产业相依关系能为我国是否已形成以技术进步为核心的新能源产业提供经验证据。此外,作为一个政府大力扶持的朝阳产业,新能源公司股票引起了投资者的极大兴趣;但是,新能源产业的补贴政策等“好消息”却往往引发化石能源投资者的担忧[10],而把握三产业间股价相依结构是进行投资组合优化和风险管理的前提。
在这一背景下,本文通过因果关系检验、copula建模等方法,力求对国内新能源、化石能源和高科技公司股价动态相依结构进行深入分析。与传统的描述线性关系的手段相比,copula模型能够灵活地刻画非线性的、动态的、多维的、尾部的相依关系,在能源经济学中有着良好应用[11]。与现有文献相比,本文有如下特色:第一,现有文献多局限在对线性相依关系的描述,而本文着重考察了三产业间的非线性相依关系;第二,本文不仅考察了三产业间的无条件相依关系,而且考察了控制市场收益影响后三者的条件相依关系,从一个新视角补充了Henriques和Sadorsky[3]的结论;第三,本文考察了剔除市场收益影响后新能源与高科技产业间的因果关系,对“新能源产业的兴衰很大程度依赖于特定科技的发展”这一传统观点提出了质疑。
1 数据和模型
1.1 数据
本文选取国证新能源指数(CNEI)、Wind石油天然气与供消费用燃料指数(OGCF)、Wind科技龙头指数(TL)日收盘价分别代表新能源、化石能源和高科技公司股价。出于数据可得性等考虑样本覆盖的时间范围为2010年8月31日到2020年8月31日,剔除非交易日等缺失数据后共得到2431组数据,取对数并差分后得到2430组收益率数据。数据均来源于Wind数据库。
1.2 模型
1.2.1 因果关系检验
首先考虑应用最广泛的格兰杰因果检验,这种检验适用于平稳序列或存在协整关系的单位根过程,如式(1)所示:
(1)
其原假设为H0:β1=…=βp=0,即x不是y的格兰杰原因。该检验揭示非线性关系的能力较弱,而Hiemstra和Jones[12]提出的HJ检验可以弥补这一不足。
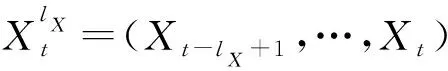
(2)
Diks和Panchenko[13]认为,HJ检验存在当原假设为真的时候过度拒绝原假设的缺点,因此他们提出了一种改良的检验,下文称为DP检验,相应原假设表示为:
(3)
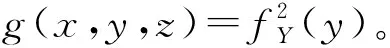
1.2.2 时变copula
本文主要利用由Patton[14]提出的时变SJC copula来捕捉CNEI、OGCF和TL两两之间的动态相依关系。SJC copula是通过改进BB7copula得来的,其主要优势为对上下尾都敏感而且既能刻画对称的尾部关系也能刻画不对称的尾部关系,其函数表达式如下:
CSJC(u,v|τU,τL)=0.5·(CBB7(u,v|τU,τL)+
CBB7(1-u,1-v|τU,τL)+u+v-1)
(4)
CBB7(u,v|τU,τL)=1-(1-{[(1-u)k]-γ+
[1-(1-v)k]-γ-1}-1/γ)1/k
(5)
式(5)中k和γ为CBB7的参数,k=1/log2(2-τU) ,γ=-1/log2(τL) ;τU、τL分别表示上尾相关性和下尾相关性,τU∈(0,1),τL∈(0,1)。为使τU和τL随时间变化,有如下演化方程:
(6)
(7)
其中logistic变换Λ≡(1+e-x)-1使得τU和τL在上文规定的范围内取值。
作为尾部相依性的补充,利用时变Claytoncopula导出两指数间相关性测度Kendall相关系数τ,这种copula的参数与τ具有一一对应关系,τ的演化方程与式(6)、(7)类似。
1.2.3 滚动窗口R藤copula
尽管时变copula能够对相关性测度随时间变化的情况进行参数化的表达,但其参数估计并不总是显著的,且函数形式即copula类型的选择余地较小。作为一种备择的解决方案,本文采用滚动窗口R藤copula来刻画OGCF、CNEI和TL的关系。同时,从图1可以看出,CNEI、OGCF和TL与用沪深300指数(CSI300)表示的市场股价走势的关联程度都很高,由于市场收益的主导作用OGCF、CNEI和TL两两之间有较强的正相依关系也不足为怪;结合前文所述,一个令人感兴趣的问题是当去除市场收益的主导作用后CNEI、OGCF和TL两两之间的相依性如何。本文通过指定R藤copula的结构将市场收益率作为条件,从而得到在排除市场收益的影响后三指数两两之间的相依性测度,并采用滚动窗口法捕捉相依性的动态特征。
R藤copula模型[15]的基本目的是用仅用成双copula(pair copula)为元素构建多个变量的联合分布函数。为给出R藤定义,首先引入树的概念:图T=(N,E)为一棵树,如果对顶点集N={v0,v1,…,vk}中任意两个顶点都有一条唯一的边相连。由(d-1)棵树构成的集合V={T1,…,Td-1}为一个d维R藤,如果对任意一棵树Tj=(Nj,Ej)的任意两个顶点a,b∈Tj,j=1,…,d-1,都存在一条路(path)n1,…,nk⊂Nj,使得a=n1,b=nk;第一棵树T1有顶点集N1={1,…,d}及边集E1;对j≥2,树Tj有顶点集Nj=Ej-1及边集Ej;对j=2,…,d-1及{a,b}∈Ej,|a∩b|=1。记R藤中一边为e=(Ce,a,Ce,b|De),其中Ce,a和Ce,b为该边两端的条件顶点,De为条件集,与e对应的copula密度函数为cCe,a,Ce,b|De。设随机向量X=(X1,…,Xd),其中分量Xk的边际密度为fk,R藤分布被定义为能够分解为式(8)的随机向量X的联合概率密度函数。
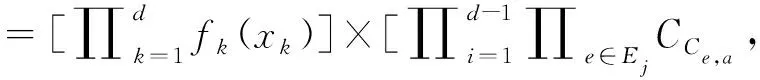
Ce,b|De(F(xce,a),F(xce,a) |xDe))]
(8)
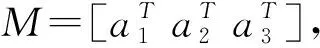
根据滚动窗口的窗宽和步长(设窗宽为250个交易日,步长为1个交易日),拟合[(样本长度-窗宽)/步长+1]个R藤copula模型,这种做法可一定程度克服时变copula的局限性。
2 实证研究
2.1 描述统计
根据表1,OGCF的标准差即波动性最小,这与Zhang和Du[8]的发现一致,他们认为这跟中国政府旨在稳定化石能源价格的调控政策有关。三序列偏度均小于0,说明负收益率出现频率更高;其中OGCF尖峰的特征最明显;ADF和PP检验表明三序列是平稳的;SW正态性检验说明三序列均非正态分布;Ljung-Box检验表明OGCF和TL存在线性序列相关,而三序列均有波动聚集现象。从图1可以看出,各序列之间存在明显的同涨同跌的现象,但是在大涨大跌的情况下涨跌的幅度却差异较大,这暗示了大于0的相依性测度和不对称的尾部相依结构。

表1 收益率序列描述统计

图1 OGCF、CNEI、TL和CSI300日收盘价
2.2 因果关系检验
首先分别对OGCF、CNEI和TL进行线性格兰杰检验,结果见表2;然后根据AIC信息准则拟合三个最优滞后阶数的二元VAR模型(OGCF与CNEI、OGCF与TL、CNEI与TL),对其过滤出的残差序列进行非线性格兰杰检验,结果见表3。如表所示,在线性层面,TL是CNEI的格兰杰原因、OGCF和TL中至少有一个是CNEI的格兰杰原因,这说明高科技公司股价对预测新能源公司未来股价有较为显著的作用;CNEI只有在滞后一阶时是TL的格兰杰原因,其“预测能力”的时效要短得多;除此之外,没有任何变量之间存在格兰杰因果关系。这说明在三指数中CNEI和TL之间有着相对密切的关系;同时,在CNEI和TL可能存在的正向相依关系中,TL将占据相对主导地位——这与Sadorsky[4]的发现一致。在非线性层面,三指数间的关系较为复杂,任意一对都互为格兰杰原因,一定程度说明使用非线性计量模型分析三者相依结构的必要性。

表2 线性格兰杰因果关系检验

表3 非线性格兰杰因果关系检验
2.3 时变copula建模
在copula建模之前,需对各序列边缘分布进行拟合使其经过概率积分变换后服从标准均匀分布,得到“伪copula数据(pseudo-copuladata)”。对金融时间序列通常拟合GARCH(1,1)模型,根据数据特征也可拟合不同类型的GARCH模型进行比较后择优使用。在另一方面,Kim et al.[16]研究表明,copula的拟合结果对边缘分布的设定并不十分敏感,除非边缘分布被严重误设;Czado[17]补充到,鉴于尖峰厚尾等普遍特征,在金融时间序列的copula建模中t-GARCH(1,1)模型可作为一种拟合边缘分布的通用方法。本文沿用这一方法,用t-GARCH(1,1)对CNEI、OGCF和TL的收益率序列进行拟合,结果见表4。从Ljung-Box检验结果可以看出,滤出的残差序列均不存在线性序列相关和波动聚集现象;KS检验结果说明对残差的t分布假定是适当的。综合来看,t-GARCH(1,1)模型较好拟合了三序列的边缘分布,因此通过对残差进行基于t分布的概率积分变换得到服从标准均匀分布的“伪copula数据”,如图2所示。相比对原始数据绘制散点图,图2可以更加直观地比较尾部相依关系。从图中可以看出三对关系都存在(0,0)附近数据点比(1,1)附近数据点更密集的情况,据此可以粗略判断它们之间的下尾相关性均大于上尾相关性,而本文所选的SJC copula可以较好地描述这种不对称的尾部关系。

表4 t-GARCH(1,1)模型拟合结果
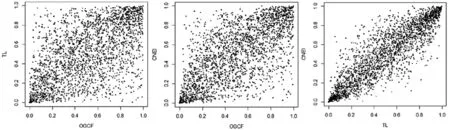
图2 标准均匀分布散点图
接下来对三序列两两之间分别拟合时变SJC copula和时变Clayton copula,结果如表5所示。可以看出,对于OGCF-CNEI和OGCF-TL两对关系,给定5%的显著性水平,时变SJC copula演化方程中的参数全部显著,说明其较好地捕捉了这两对关系中τU和τL的时变特征;但是在CNEI-TL中,τU的演化方程和τL的演化方程中均有不显著的参数,因此其导出的尾部相关性测度是不可靠的。为解决这一问题拟合滚动窗口SJC copula以描述CNEI-TL尾部相依性的时变特征,令窗宽为250个交易日,步长为1个交易日,共得到2181个静态SJC copula模型,其尾部相关性测度均在5%水平上显著。此外,对于OGCF-CNEI、OGCF-TL和CNEI-TL三对关系,给定1%的显著性水平,时变Claytoncopula演化方程中的参数全部显著,说明其较好的捕捉了三对关系中τ的时变特征;从Beta值来看,与OGCF-CNEI和OGCF-TL不同的是,t期CNEI-TL的τ受到t-1期τ显著的正向影响,说明其相关性具有一定的持续性;例如,如果在t期CNEI-TL为高度正相关,投资者在一定程度上可以期望在t+1期他们仍为高度正相关。将表中参数估计值代入演化方程中,即可得到时变相关性测度,见图3。可以看出,CNEI-TL三种相关性测度的均值均为最高,但CNEI-TL与OGCF-CNEI、OGCF-TL的相关性测度差距不大且均为正值,这可能是由于三指数均来自沪深两市,同受市场收益主导作用的影响。
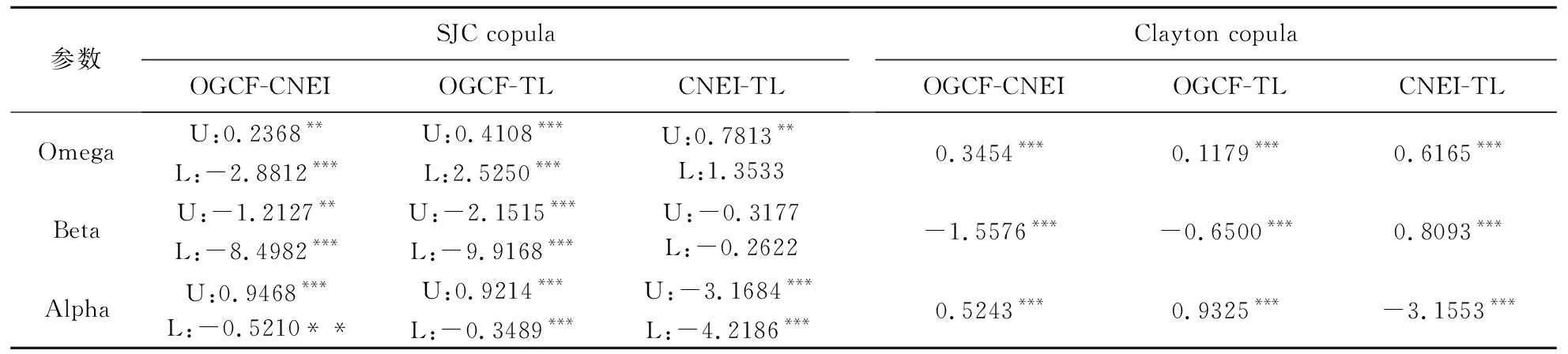
表5 时变copula演化方程拟合结果
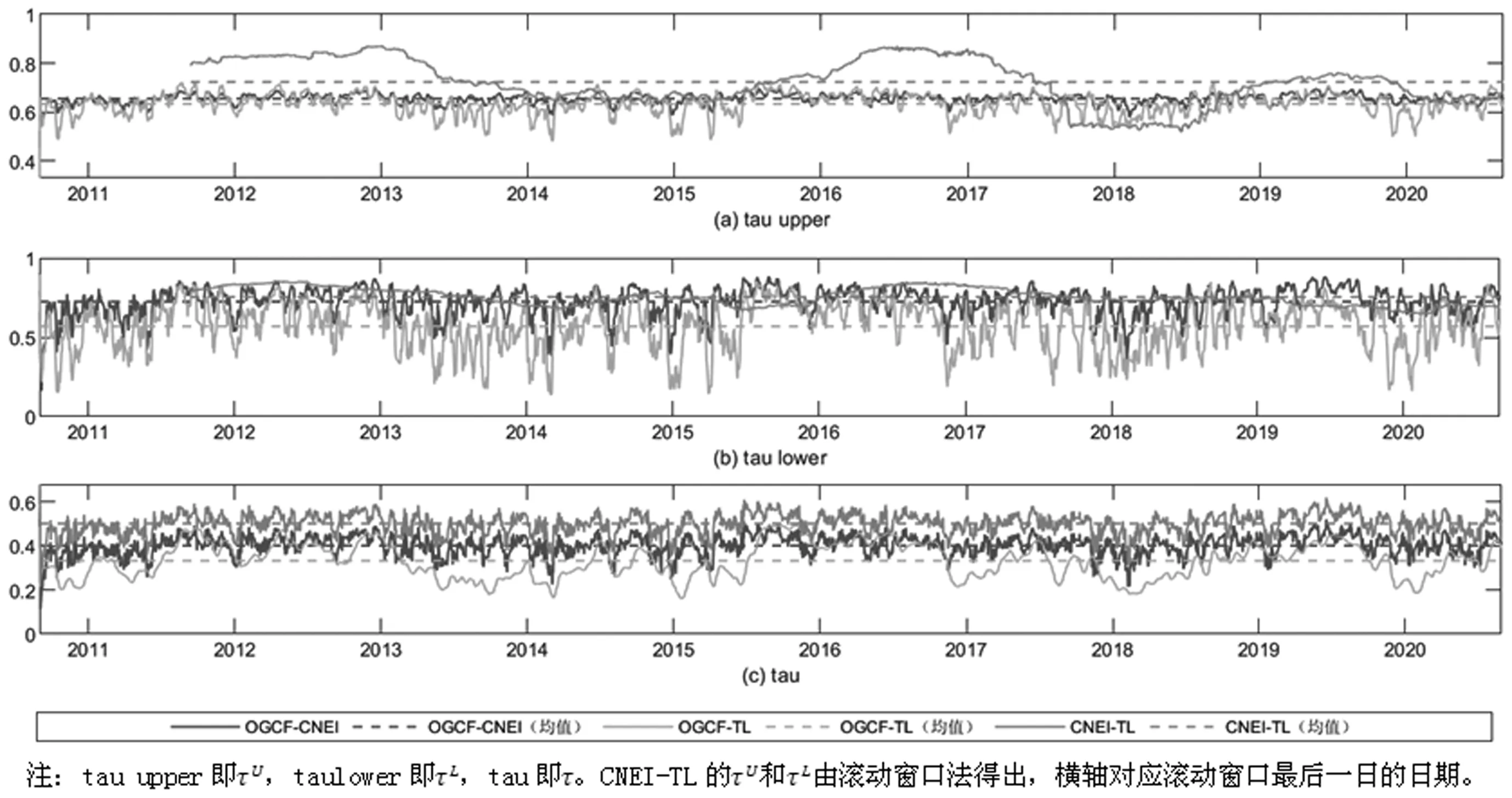
图3 时变copula导出的相关性测度
2.4 滚动窗口R藤copula建模
由前文分析可知,我们期望在通过R藤copula模型去除市场收益的作用后各相关性测度的值会有明显降低,同时相关性测度间的差异会更明显。对于R藤第一棵树对应的成双copula类型,本文不做具体规定,而是按AIC信息准则从常用的十余种(以及它们的旋转)copula中择优选取,如此可以最大化第一棵树的拟合优度;国内采用滚动窗口R藤copula的文献多规定全部成双copula类型,相比之下本文的设定更灵活。对于第二棵树的成双copula,本文规定其为t-copula,因为这种copula可同时适应正负相关性测度以及尖峰厚尾特征。通过滚动窗口技术,对于OGCF-CNEI、OGCF-TL和CNEI-TL中的任意一个,都拟合2181个三维R藤模型;R藤第二棵树对应的成双copula分别为COGCF, CNEI; CSI300、COGCF,TL; CSI300和CCNEI,TL; CSI300,对应的相关性测度τ见图4(a)、τU和τL见图4(b);作为参照,图中同时给出了无条件的t-copulaCOGCF, CNEI、COGCF, TL和CCNEI,TL导出的相关性测度。
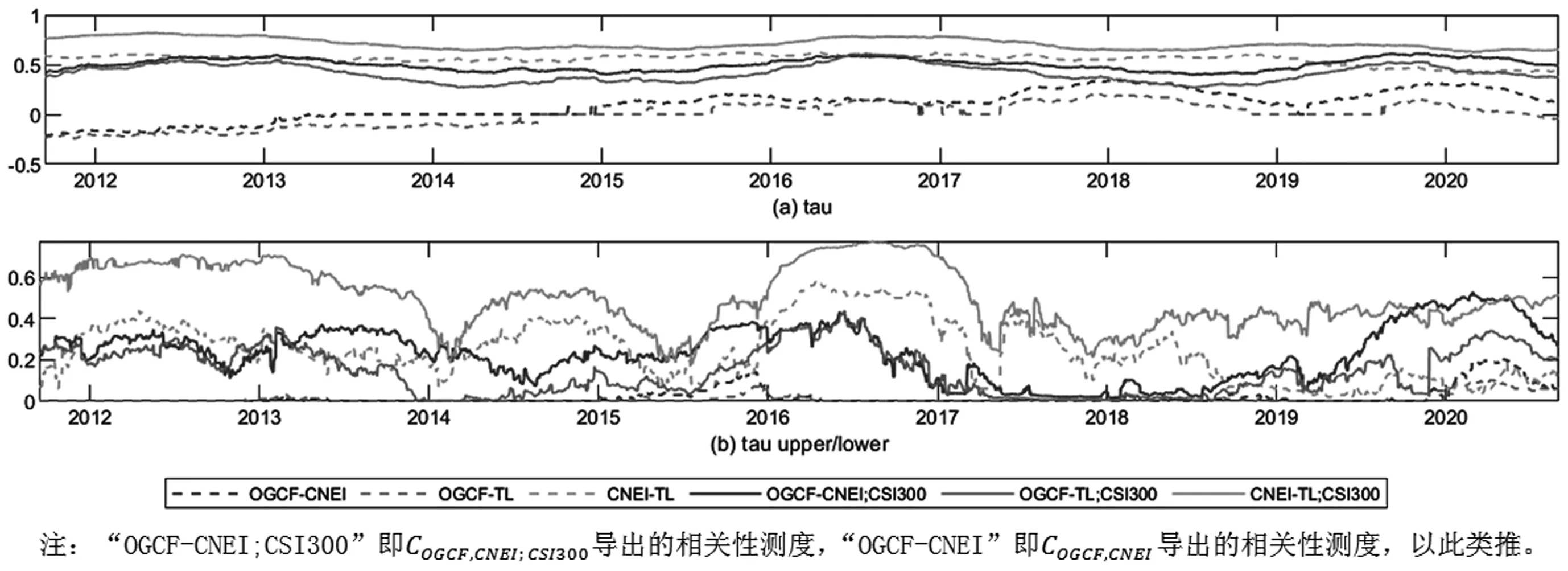
图4 滚动窗口R藤copula导出的相关性测度
如图所示,在将市场收益作为条件后OGCF-CNEI、OGCF-TL和CNEI-TL相关性测度的值都明显降低,相互之间的差异更加鲜明。OGCF-CNEI、OGCF-TL出现了负相关的情况,且在多个时期不存在相依关系;相对而言,CNEI-TL的τ较为稳定并一直处于高位,这与通过时变copula得出的结论一致,即新能源和高科技产业具有更多的相似之处。从绝对值来看,在控制市场收益的影响后CNEI-TL的τ均值在0.5以上。综上,可以发现在投资者视角中我国的新能源产业和高科技产业已具有较高的同质性,而且这种同质性已经超过了新能源与化石能源即能源产业这一整体的同质性,这间接肯定了我国以技术进步为核心的新能源发展战略的有效性。
在另一方面,从2018年末至今,CNEI-TL的τ呈现下行趋势并伴随着OGCF-CNEI的τ的上升,这可能是新能源产业日渐发展成熟的结果:随着创新和技术迭代的速度越来越慢、技术瓶颈越来越难突破,新能源产业的股票表现开始变得更接近化石能源产业而逐渐远离高科技产业。从整个样本时期来看,尽管CNEI-TL始终在高位,但其与OGCF-CNEI的τ差距逐渐缩小。同时,图4(b)表明CNEI-TL的尾部相关系数波动剧烈,这可能与新能源产业的政策依赖性有关:在财政补贴等扶持政策红利期,新能源公司股价往往迎来大涨,其估值和联动性向高科技公司看齐;在政策真空期、补贴退坡等政策落地后,新能源公司股价往往迎来大跌,其估值和联动性向化石能源公司看齐。这一定程度说明,投资者之所以将新能源和高科技产业视为一个整体,是因为扶持政策的存在,而在政策退坡后,新能源产业能否继续保持其高科技属性还未可知。
2.5 因果关系的进一步检验
鉴于文章不仅描述三产业间的无条件相依关系,而且考察剔除市场收益影响后的条件相依关系,因此需进一步确定剔除市场收益影响后的因果关系。Baykut和Kula[18]给出了一种剔除市场收益影响的方法:考虑回归方程OGCFt-CSI300t=α+εt,t=1,…,2430,拟合得到的残差序列ε1,…,ε2430反映了OGCF剔除市场收益影响后的“净”信息。令窗宽仍为250个交易日,步长为50个交易日,对剔除市场收益影响后的残差序列进行滚动窗口格兰杰因果检验;限于篇幅,仅给出关系相对密切的CNEI和TL的检验结果,如图5所示。综合线性和非线性层面来看,TL对CNEI的引领作用并不稳定,仅在特定时期出现,这对“新能源产业的兴衰很大程度依赖于特定科技的发展”这一被广泛引用的观点[4]提出了质疑——尽管TL对CNEI的引领作用并非偶然现象,但这种因果关系并非长期的、稳定的;相比之下,CNEI对TL的引领作用是非常稳定的——这种对比指出了一种更加可能的情况,即与其说“新能源产业的兴衰很大程度依赖于特定科技的发展”不如说“特定科技的发展很大程度依赖于新能源产业的兴衰”。
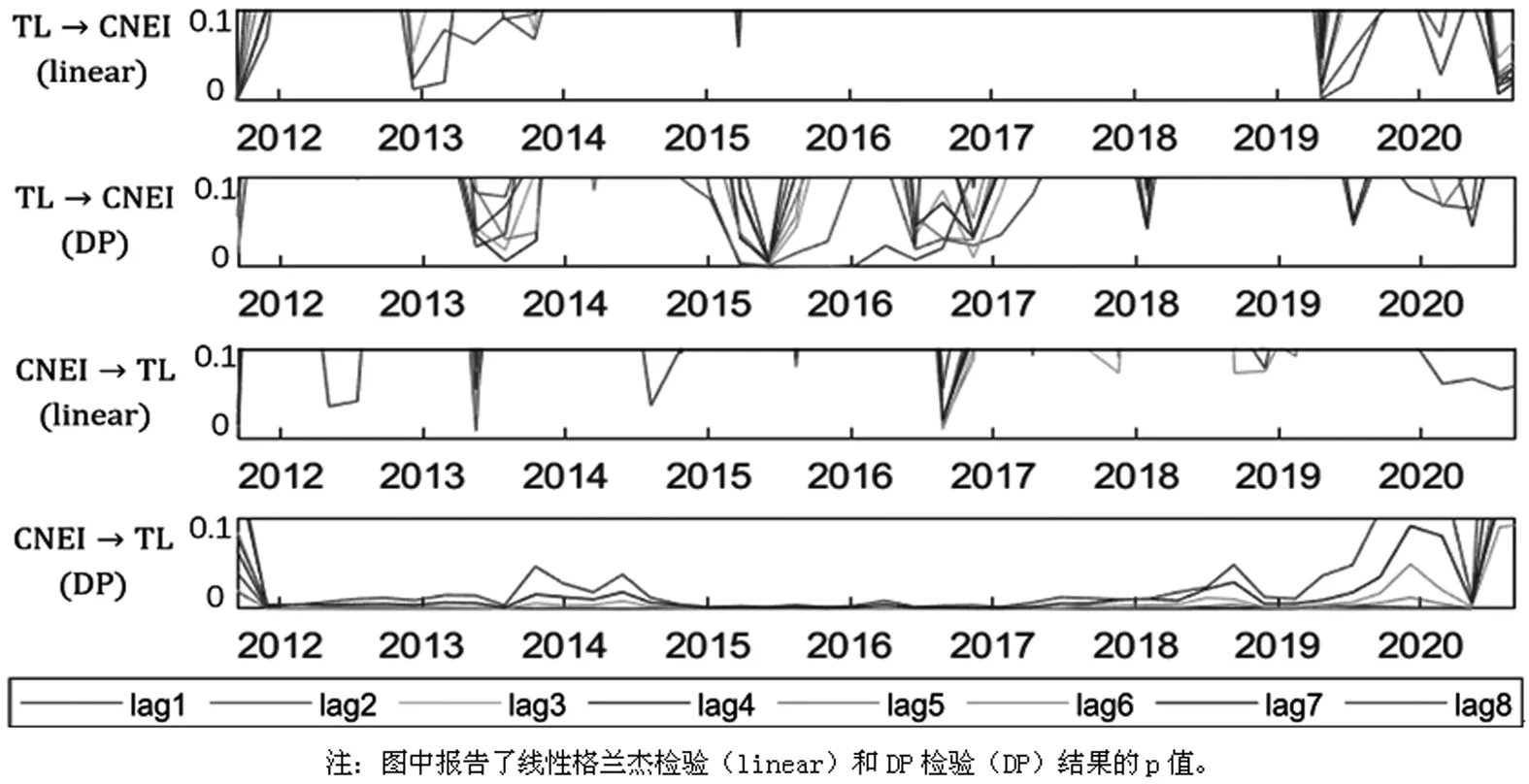
图5 剔除市场收益影响后的滚动窗口格兰杰因果关系检验
3 结论与建议
本文将新能源、化石能源和高科技公司纳入同一分析框架,采用因果关系检验确定了三种资产间的先导关系,利用时变copula、滚动窗口R藤copula模型描述了三种资产的相依结构,并分析了新能源和高科技公司间剔除市场收益影响后的动态因果关系,主要结论如下:新能源与高科技产业具有密切的联动关系,新能源与高科技产业展现出比能源产业内部更高的同质性;在样本时期内新能源-高科技相依性减弱、新能源-化石能源相依性增强;新能源-高科技尾部相依性波动剧烈,新能源产业的高科技属性或依赖于扶持政策;对“新能源产业的兴衰很大程度依赖于特定科技的发展”这一传统观点提出了质疑,给出了一种与实证结果一致的备择观点。
基于以上结论,本文提出如下建议:对政策制定者而言,应当加强扶持政策的针对性,避免扶持“新能源”这一先进概念中的落后产能;同时,应当着眼于培育我国新能源产业可持续的创新能力,而不是在扶持政策退坡后很快丧失其高科技属性。对投资者而言,由于三种资产具有较强的正向相依关系,不适合用来构建投资组合;设市场收益为条件后三种资产的相依性大幅降低,出于分散风险考虑跨市场资产配置或优于同一市场中的跨行业资产配置;持有新能源公司股票的投资者有必要对其收益率和其与其他资产的相依性进行政策变动的敏感性测试。

