基于需求不确定的集装箱港口集疏运鲁棒优化
——以大连港和营口港集装箱集疏运网络为例
吴泽昕,王鸿鹏
(集美大学航海学院,福建 厦门 361021)
0 引言
随着全球集装箱运输量的不断攀升,对港口集疏运网络运作能力提出了更高的要求。近年来,不少专家学者致力于港口集疏运网络优化研究。魏海蕊等[1]、庄佩君等[2]以无水港建立为基础,研究集装箱港口集疏运货流分配的规划模型;范厚明等[3]通过设定需求情景表达不确定需求来研究内陆港的选址问题;Carlos 等[4]考虑需求和运输成本双重不确定性对中转站选址的影响;Yin 等[5]研究了考虑碳排放的港口腹地间多式联运货运组织;张旭等[6]研究了基于分段累进碳税的需求不确定情况下多式联运路径选择问题;Zha等[7]重点介绍了网络流量对多模式运输网络的影响,提出了港口集疏运网络的流量模型;文献[8-10]建立了广义最小运输成本的集疏运网络配流模型,研究了不同海港或地区港口集疏运网络。
有效利用现有集装箱港口集疏运网络资源,合理分配集装箱货运量,对港口集疏运网络实现高效运作、降低运输成本、减少环境污染物排放具有重要作用。现有文献多数在选址问题、路径选择问题中研究运输需求的不确定性,对货流分配中的运输需求不确定性问题少有研究。文献[11-16]运用随机规划、区间规划、情景鲁棒等方式处理运输需求不确定性,并以某些地区港口集疏运网络为例得出港口集疏运网络配流的最佳方案。其中,随机规划需事先明确不确定需求的分布概率,但通常难以估计;区间规划和情景鲁棒对于运输需求复杂的现实情况的描述十分有限,且未考虑不同决策者对不确定性因素的风险偏好。此外,多数研究仅对集装箱集运或疏运进行分析,而集运和疏运是相互关联的,为了避免集运和疏运分开设计所产生的次优性,需对集疏运网络双向货流分配进行研究。
针对港口集疏运配流研究的不足,采用盒式不确定集合对不确定需求进行描述,建立港口集疏运网络运输最小二氧化碳排放量、最小二氧化硫排放量、最短总运输时间以及最小总运输成本的多目标双向集疏运网络配流鲁棒优化模型,从而规避由于不确定运输需求量描述的局限以及集疏运网络设计不完善导致的最优集疏运网络货流分配方案的偏差。通过对大连港和营口港集装箱集疏运网络进行实例分析,验证所建模型的有效性,以期为不确定运输需求下集装箱港口集疏运网络货流分配优化提供新的解决思路以及更全面的解决方案。
1 问题描述与模型建立
1.1 问题描述
为提升港口集疏运网络运输能力,需对港口集疏运网络货流量进行合理分配。现实情况中,港口集疏运网络运输需求受到多种不确定性因素的影响,在不同时期呈现出一定的波动性,在模型建立过程中对不确定运输需求进行处理,进而考虑运输过程中产生的环境污染物排放量,运输时间、运输成本、运输能力等限制,通过建立多目标港口集疏运配流鲁棒优化模型,得到港口集疏运网络最低运输成本、最短运输时间、最少环境污染物排放量的货流分配方案,并实例验证。
将集装箱港口集疏运网络描述为由腹地城市节点、集装箱中转站节点、沿海集装箱港口节点以及相邻节点间运输线路构成的简单网络。集装箱货物由腹地城市运向港口为集运,反之为疏运。集装箱货物在腹地城市与港口之间可以通过公路和铁路两种方式进行直达或者中转运输。为将复杂的港口集疏运网络货流分配问题抽象成数学模型,作出以下假设:集装箱均使用标准箱(twenty feet equivalent units,TEU),不考虑同城节点集装箱短途运输成本与碳排放成本,各种运输方式状态良好,各种运输方式之间的转换只能在节点处发生。
1.2 符号定义
a:腹地城市的个数;
b:集装箱中转站的个数;
c:港口的个数;
W:模型可行解的目标函数值;
M:运输方式集合,m为运输方式编号,m∈M,1 为公路运输,2 为铁路运输;
Cijm:腹地i到港口j以m方式运输的单位集装箱运输成本,元·TEU-1;
bk:集装箱中转站k的单位集装箱中转费用,元·TEU-1;
Tk:集装箱中转站k的单位集装箱中转换装所需平均时间,h·TEU-1;
COijm:腹地i到港口j以m方式运输的单位集装箱二氧化碳排放量,kg·TEU-1;
SOijm:腹地i到港口j以m方式运输的单位集装箱二氧化硫排放量,kg·TEU-1;
Tijm:腹地i到港口j以m方式运输的单位集装箱所需时间,h·TEU-1;
Xijm:腹地i到港口j以m方式运输的集装箱量,TEU;
:腹地i的集装箱供给量,TEU;
:腹地i的集装箱需求量,TEU;
Rj:港口j的集装箱吞吐能力,TEU;
Ok:集装箱中转站k的转运作业能力,TEU;
Lijm:腹地i到港口j以m方式运输的道路可用容量,TEU。
1.3 模型建立
1.3.1 不确定性优化模型
通过考虑集疏运网络中转站、港口的作业能力以及各运输方式运输能力的约束,并以集疏运网络最少二氧化碳排放量、最少二氧化硫排放量、最短运输时间以及最小运输成本建立多目标集疏运网络货流分配模型,如下所示:
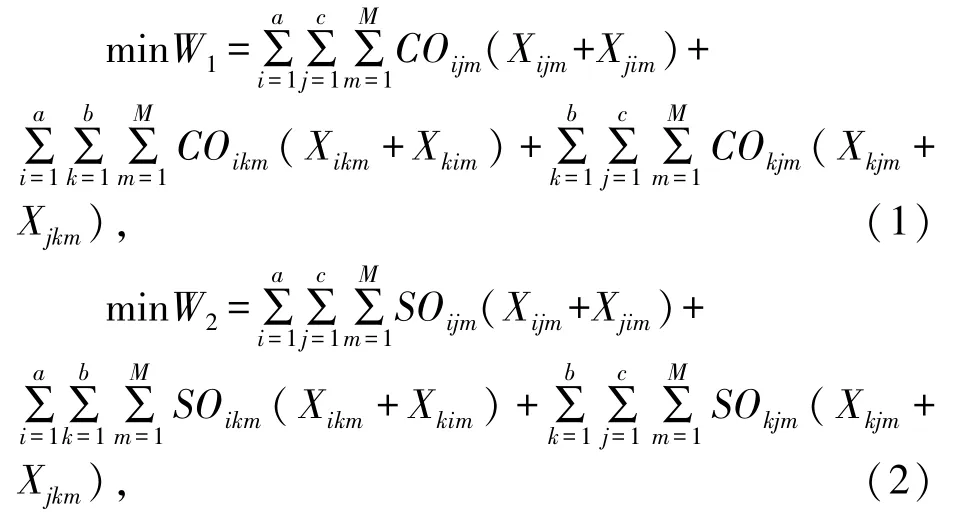
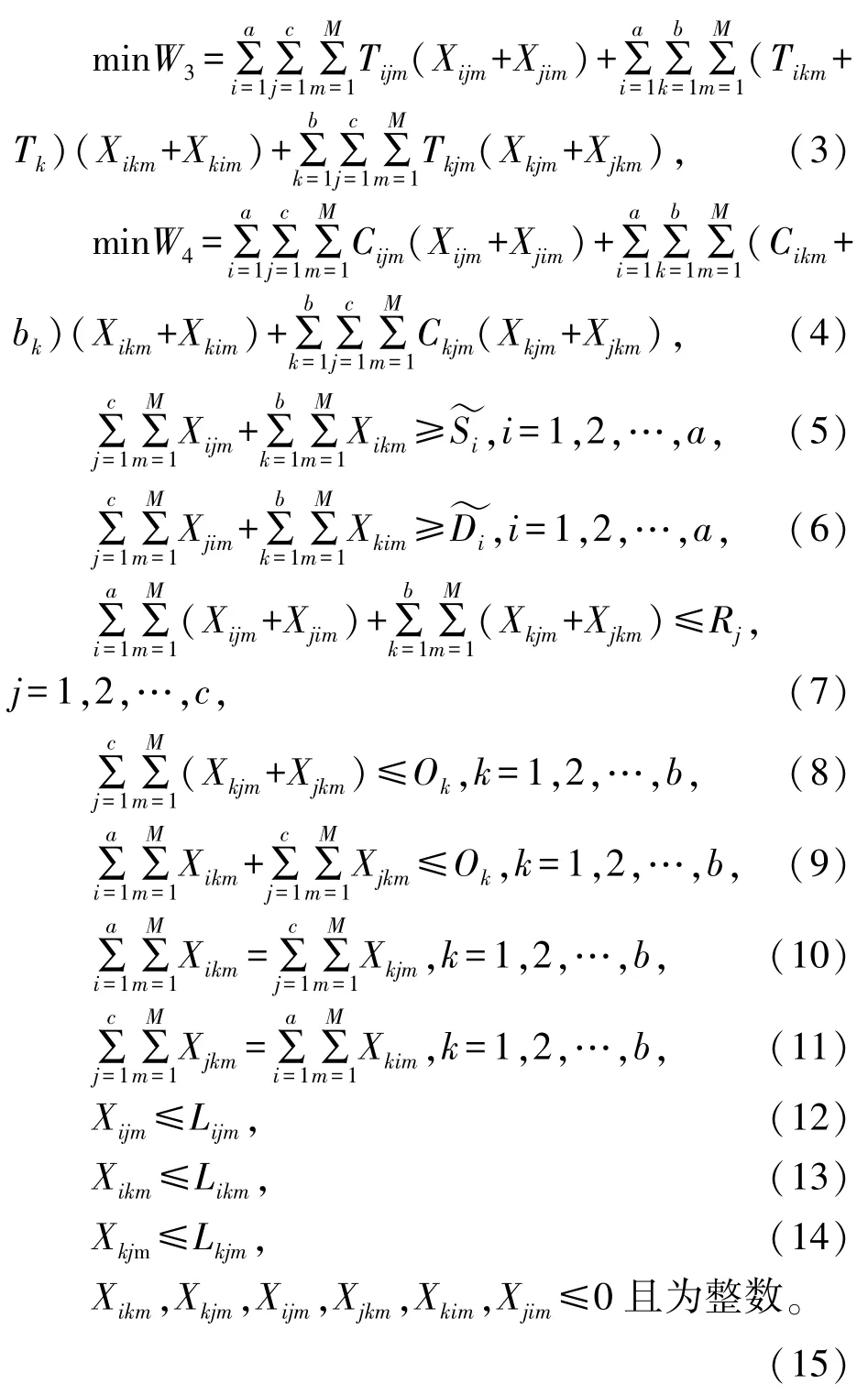
式(1)~式(4)表示模型的目标函数值,即集疏运网络二氧化碳排放量最小、二氧化硫排放量最小、集装箱总运输时间最短以及集装箱中转存储费用与运输费用之和最小;式(5)表示集运集装箱量等于腹地集装箱供给量;式(6)表示疏运集装箱量等于腹地集装箱需求量;式(7)表示集装箱港口服务能力受其吞吐能力约束;式(8)、式(9)表示集装箱中转站服务能力受其转运能力约束;式(10)、式(11)表示中转流量平衡约束,即集装箱中转站进货量等于出货量;式(12)~式(14)表示各运输方式运输能力约束;式(15)表示决策变量非负整数约束。
1.3.2 鲁棒对等问题优化模型
集疏运网络集装箱运输需求由于受到多种不确定性因素的影响,在不同时期呈现出一定的波动性,但其波动情况并不服从某一具体概率分布,相应的模糊隶属函数也无法确定,而鲁棒优化可以规避上述问题,所以采用鲁棒优化方法对运输需求不确定性进行处理。
在式(5)、式(6)中有不确定性运输需求量和,将其所在约束条件进行鲁棒等价模型转化。对于运输需求的不确定性构建不确定集合对其进行描述,使用盒式不确定集合描述运输需求量不确定水平,假设腹地城市i的集装箱运输需求量为为名义需求量;为相对于名义需求量的最大偏差,其中εi为扰动比例;由于不确定性运输需求量和为所在约束条件的右手边项,根据Hatefi 和Jolai[17]提出的关于约束条件右手边不确定项鲁棒对等转换方法,对式(5)和式(6)进行转换,得到如下约束条件:
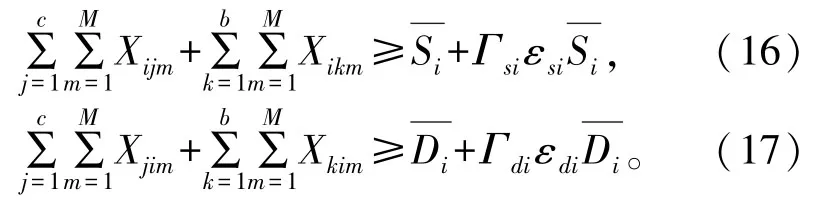
式中,Γi为不确定性预算,表示需求不确定性的水平,反映了决策者对于运输需求不确定的风险偏好程度,Γi∈ [0,1]。Γi越小,表明决策者风险偏好程度越高;Γi=0 时,模型等价于确定性模型;Γi=1时,不确定运输需求均可以取到最大偏差。
2 算例分析
2.1 参数取值
以大连港和营口港集装箱集疏运网络为例进行模型分析,其中东北三省及内蒙古自治区东部地区的36 个城市(其中包括集装箱中转站所在城市)作为港口腹地城市节点,沈阳、长春、哈尔滨既是腹地城市节点又是中转站节点。参考文献[13][18]得到各腹地城市集装箱供需量平均值,将其作为集装箱集疏运网络运输名义供需量,如表1所示。3 个集装箱中转站相关参数如表2所示。营口港和大连港的集装箱吞吐能力分别为200 000 TEU、350 000 TEU。各运输方式的运输能力由各城市可用的集装箱运输车数量以及每周节点城市间运行的集装箱班列确定。参考文献[15]计算得到公路和铁路每千米标准箱的二氧化碳、二氧化硫排放量,如表3所示。参考文献[19]各运输方式运输成本由运输过程中产生的费用以及装卸费用组成,具体费用取值如表4所示。鲁棒优化模型中不确定运输需求量取决于Γi和εi的取值,不确定性预算Γi∈ [0,1],取扰动比例εi分别为10%、30%、50%进行分析。
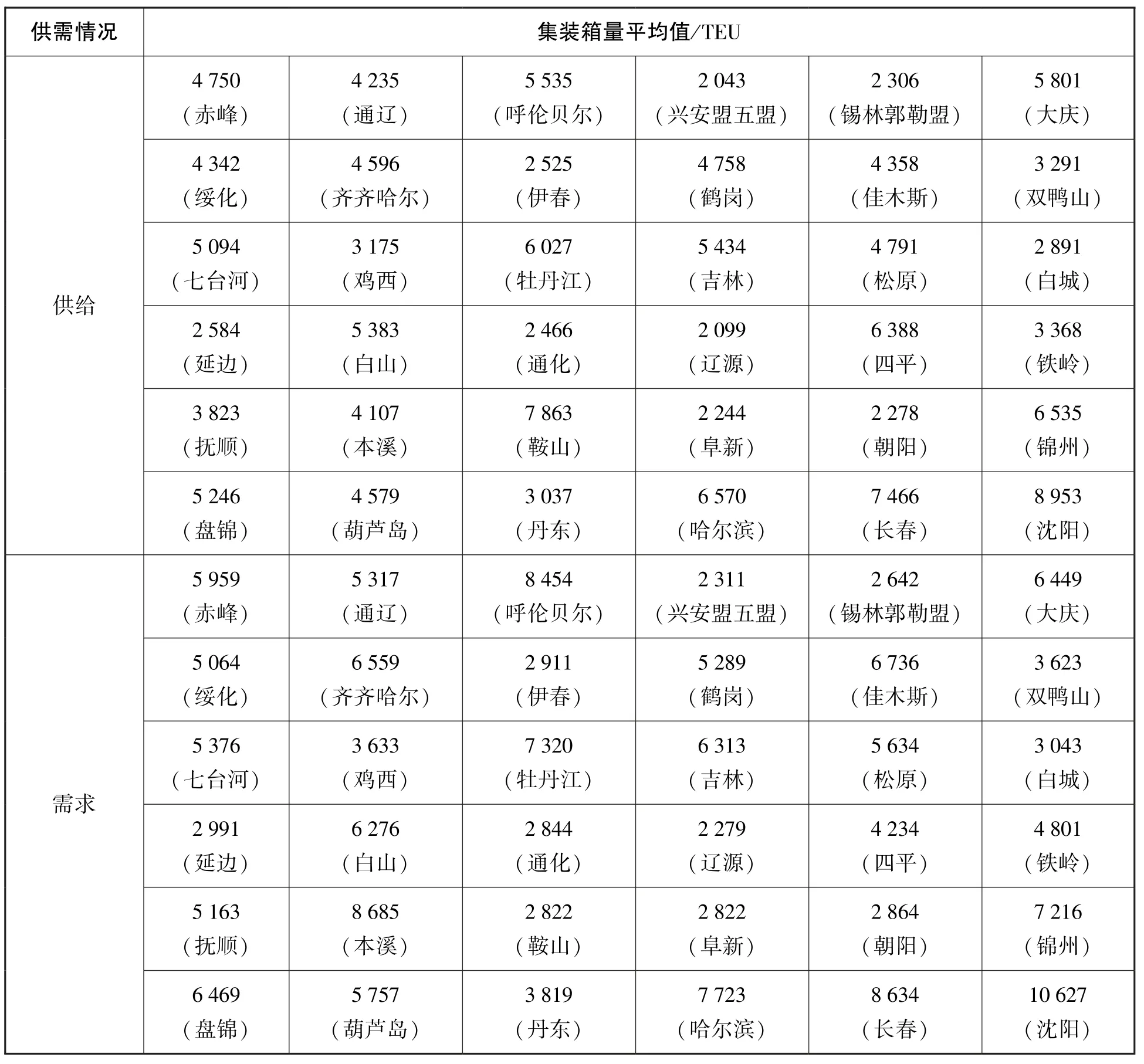
表1 各腹地城市集装箱名义供需量统计

表2 集装箱中转站平均中转时间及中转费用

表3 各运输方式单位CO2、SO2 排放量
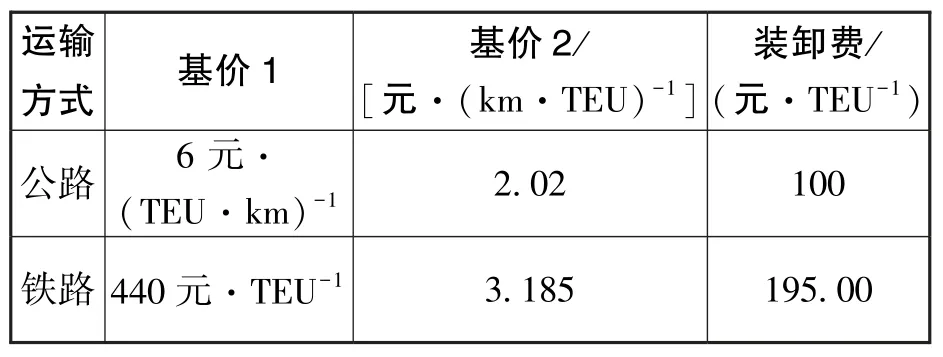
表4 各运输方式单位运输费用
2.2 结果分析
根据上述大连港和营口港集装箱集疏运网络具体数据,使用Gurobi 求解软件编程求取结果,得到不同不确定水平和不同扰动比例下集疏运网络货流分配方案。为方便对比分析决策方案效果,对Γi以0.1 为间隔进行取值。
2.2.1 确定性优化模型决策结果分析
当Γi为0 时,无论扰动比例εi取10%、30%或50%,求得的货流分配方案是相同的。确定性优化模型下,货物集疏运过程中二氧化碳的排放量为 182 926 303 kg,二氧化硫的排放量为63 896 820.42 kg,运输总时间为3 330 813.60 h,运输成本为1 626 501 595.5 元。具体集疏运货流分配方案如表5所示,表中的“/”左右分别为公路运输和铁路运输的集装箱量。在整个集装箱港口集疏运过程中,公路运输承担的货运比例为72.97%,铁路运输承担的货运比例为27.03%,主要原因是受东北三省铁路运输能力的限制,大多数集装箱货物只能选择运输成本更高的公路运输。大连港和营口港所收发的集装箱量占比分别为42.8%和57.2%,其中,营口港收发集装箱中的89.24%由公路运输承担,仅有10.76%的集装箱由铁路运输承担;相较于营口港,大连港铁路运输发展更完善,集装箱运输方式相对平衡,公路和铁路的集装箱运量占比分别为59.9%和40.10%。此外,集疏运网络以直达运输为主,比例高达94.78%,这是因为相较于中转运输,直达运输更具成本优势。
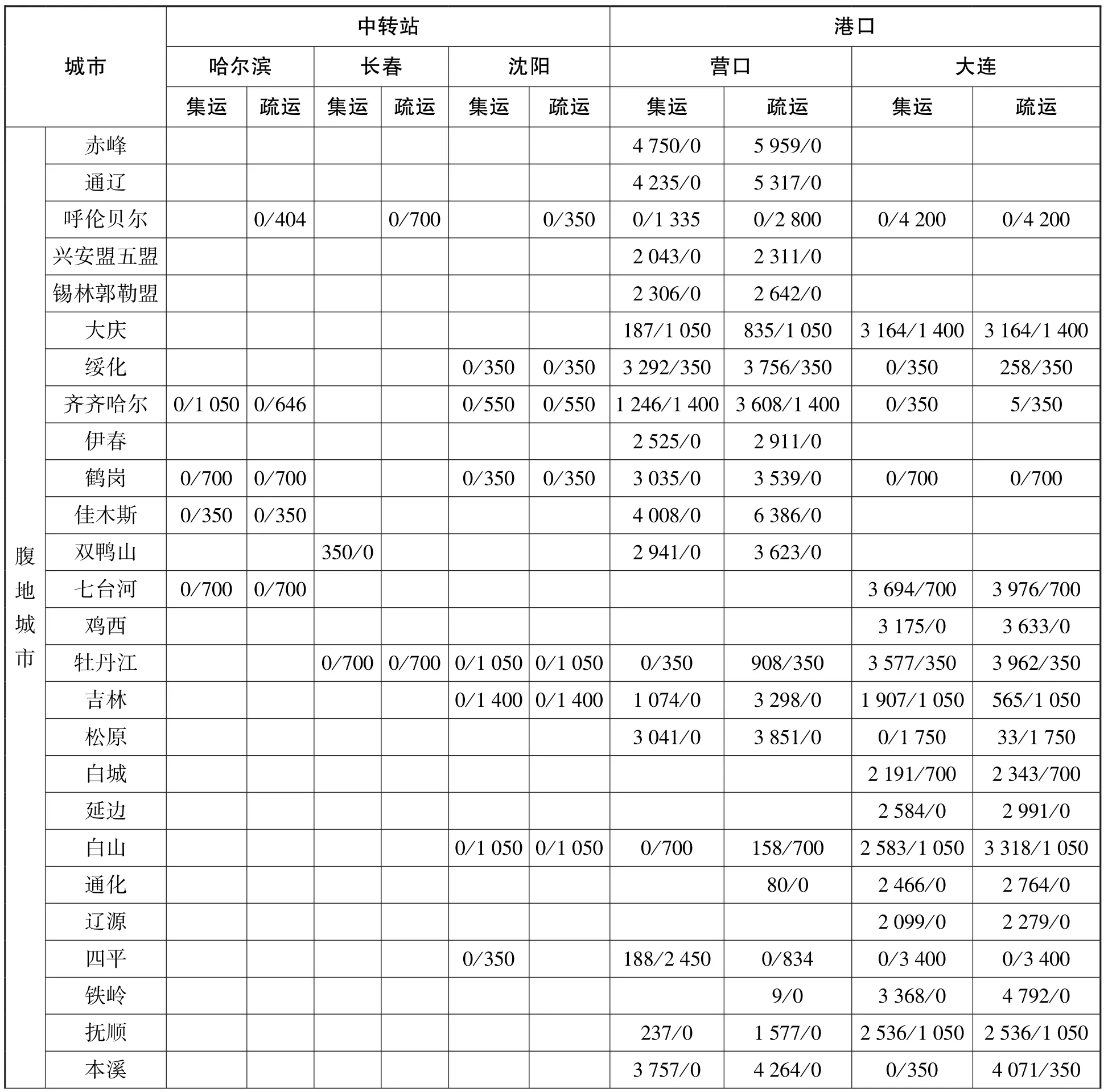
表5 确定性优化模型货流分配方案 单位:TEU
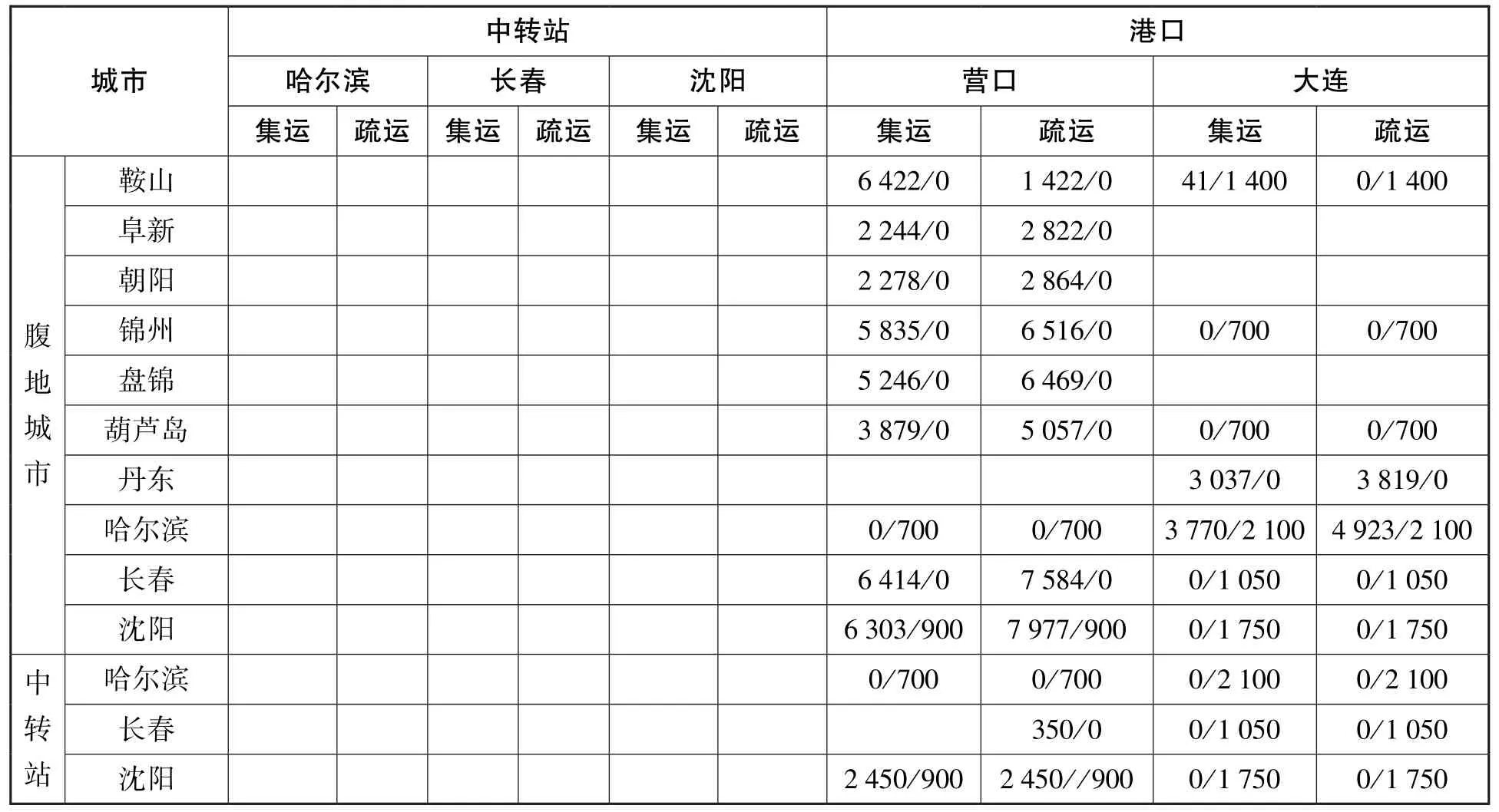
续表
2.2.2 不同的不确定性预算决策结果分析
图1为当εi=50%时,不同的不确定性预算下鲁棒货流分配方案各目标函数值相对于确定性模型各目标函数值的增加率。由图1可以看出,随着不确定性预算的增加,鲁棒优化模型下各目标函数值随之增加。但是,各目标函数值变化率有所差异,二氧化碳排放量和二氧化硫排放量增加率更高,其次为运输成本和运输时间,这说明二氧化碳排放量和二氧化硫排放量对运输需求不确定性水平更为敏感。
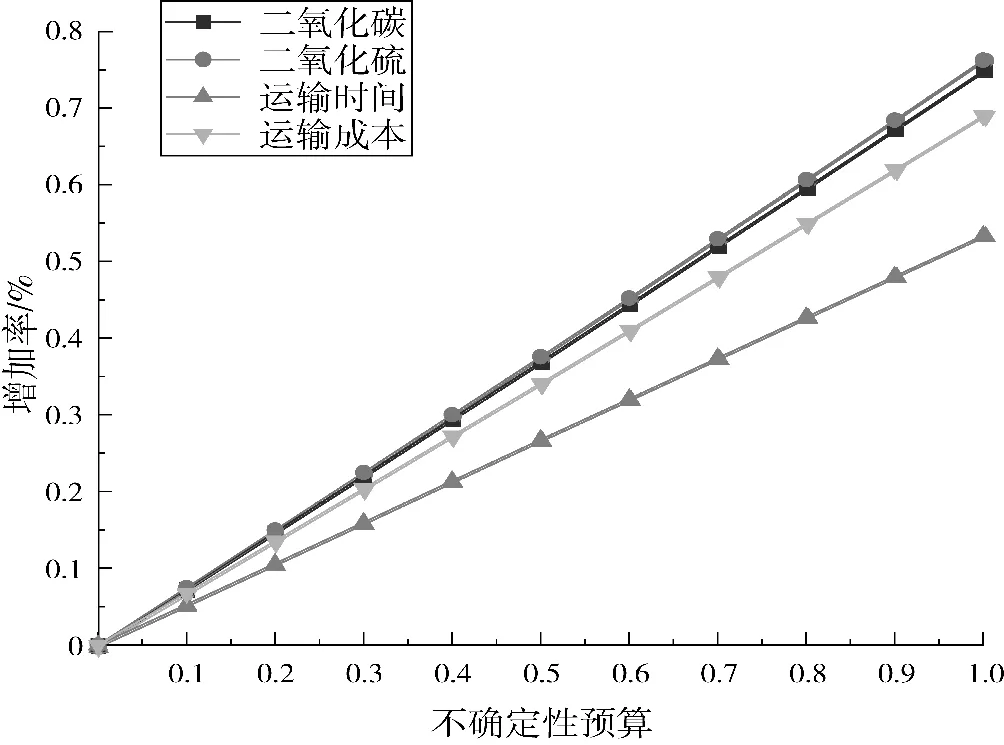
图1 不同的不确定性预算下各目标函数值的增加率
图2为不同扰动系数下二氧化碳排放量随不确定性预算增加的变动情况。可以看出随着不确定性预算的增加,二氧化碳排放量直线上升,且扰动系数越大,目标函数值增加越多。表6为Γi=1时,扰动比例为30%和50%时各目标函数值较扰动比例为10%时目标函数值的增加率。其中运输时间的增加率最低,这说明运输时间对运输需求量变化的敏感程度相较于其他3 个目标函数更低。
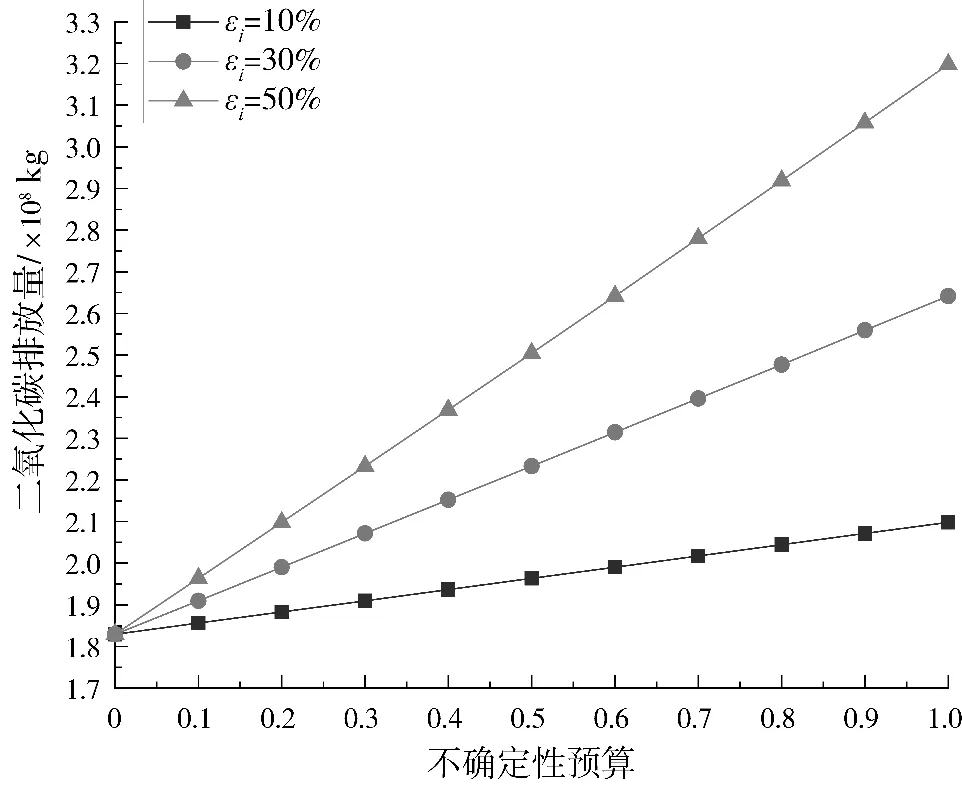
图2 不同的不确定性预算下二氧化碳的排放量
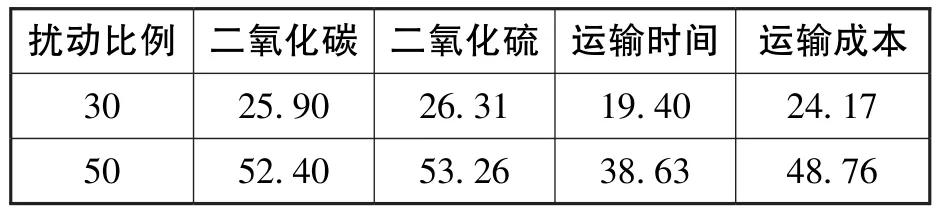
表6 Γi=1 时各目标函数值的增加率 单位:%
由图1、图2可知,不确定性预算Γi与不同目标函数值呈线性变化,这是因为不确定性预算Γi直接影响集装箱运输需求量的大小,各目标函数值与集装箱运量为线性关系,随着运输需求量的增加,各目标函数值随之增加。根据前文对确定性优化模型决策结果的分析发现,东北地区铁路运输占比较低,从而限制了集疏运网络货流分配整体优化效率,随着运输需求量的增加,有着较高运输优势的铁路运输方式较难进行组织优化,故而集装箱货物只能选择公路方式进行运输,从而使得各目标函数值直线上升。
根据本文建立的模型,不同风险偏好的决策者可以通过调节不确定性预算Γi和扰动比例εi得到相应的不确定运输需求下集装箱集疏运网络货流分配方案。追求风险的决策者可以选择不确定性预算Γi和扰动比例εi较小的分配方案,其方案在集疏运运输过程中所产生的二氧化碳、二氧化硫排放量会更少,所花费的运输时间更短,所投入的运输成本更小;规避风险的决策者可以选择较大的不确定性预算Γi和扰动比例εi,但需要付出较大的时间代价和成本代价,并且会排放更多的环境污染物。
3 结论
本文对运输需求不确定情况下的集装箱港口集疏运网络货流分配优化问题进行了研究,采用盒式不确定集合描述不确定运输需求,并对约束条件右手边不确定运输需求项进行鲁棒对等转换,通过对大连港和营口港集装箱集疏运网络配流进行实例分析,求得最小二氧化碳、二氧化硫排放量、最短总运输时间、最小总运输成本的鲁棒货流分配方案,为运输需求不确定的货流分配优化问题提供了新思路。不同风险偏好决策者可根据自身喜好调节不确定性预算和扰动比例选择不同的集装箱港口集疏运货流分配方案。追求风险者可选择参数较小的决策方案,得到最接近确定性优化的决策;反之,保守决策者可选择参数更大的决策方案,但需付出一定的代价,多种决策方案为决策者提供了更多的选择,有效地降低了决策难度。考虑到集装箱港口集疏运网络货流分配是一个系统网络优化问题,仅针对既定集疏运网络进行研究是不充分的,在后续的工作中应结合集装箱中转站选址加强集疏运网络货流分配方面的研究。

