用启发式算法设计分布式计算架构提升网络安全的可行性研究

聂祯，詹天成，徐乐，袁翔，高明

（江苏艾盾网络科技有限公司，江苏南京，210000）

0 引言

分布式技术是指用普通计算机搭建出分布式的系统架构，依靠该系统架构进行扩容，实现多数据处理。在分布式计算结构中，系统的处理任务会被不断分解，原来是依靠系统的中央处理器处理的任务，在分布式计算结构中被分解给了互联网络的各处理器，不同处理器共享系统的外设与软件，完成对任务的处理，这种处理模式可以减少中央处理器的内存负荷，让系统的逻辑结构精简化，响应速度、处理速度得到提升。但同时，处理器的增多让进程也开始增多，分布式计算结构中的主机与主机是依靠网络进行连接，因此如何维护网络安全成为确保分布式计算架构合理运行的要点。

1 分布式计算架构的组成

分布式计算系统的架构由客户服务器和分布式处理服务器共同组成，两者在计算系统中分担不同的任务，前者负责相关任务信息的发送和呈递，后者负责处理前者下发的分解任务，在完成任务分解后将最终的结果送回到前者，客户服务器节点在接收到分布式处理服务器节点后将结果信息进行融合处理，服务器节点间可以直接进行通信，比较常见的分布式计算架构设计如图1所示。

图1 分布式计算架构示意图

从图1所示，分布式计算系统对任务的处理过程涉及多主机上的多个进程，不同的服务器节点能够直接通信，如客户服务器节点是任务信息的发放点，下发的任务信息会被派送到分布式处理服务器节点，因此客户服务器节点和分布式处理服务器节点需要始终保持通信通畅，这提高了分布式系统的安全监管成本。如果安全防护措施不当，势必会引起网络安全事故，给分布式计算环境造成巨大问题[1]。故基于安全性设计的考量，分布式系统的架构组成需要进行优化处理，其蓝本如图2所示。

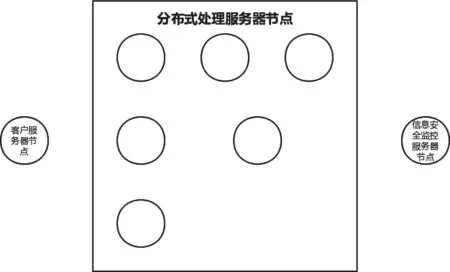
图2 以安全性为目标的分布式系统架构优化设计思路

2 分布式计算架构的安全设计思路

在信号传输时，传输的过程会形成对通信资源的占用，通信带宽对通信资源的占用主要涉及占用率以及占用的时长，两者都可以用两节点的传输距离进行等效表示。结合这一特点，在设计分布式系统的安全结构时，要注意客户服务器节点和处理服务器节点信息到达信息安全监控服务器的期望时间，所以在设计其安全结构时，任务的分解和计算过程都不是设计师的考虑重点[2]。服务器的状态，对任务情况的接受和输出结果才是设计要点。设计者要根据使用者的实际需求，对分布式任务处理器的任务接收和输出结果进行定制.提高信息传输的实时性，控制信息传输时对网络资源的占用.确保信息抵达安全监控服务器的时间在期望时间以内。

在服务器的信息传输中，有一个起始点和终止点，起始点指的是客户服务器节点发出的关于自身的信息和任务信息，该信息会被分布式处理服务器节点接收并打包，并依次向下个服务器节点传递，在打包信息抵达信息安全监控服务器后停止，在这个过程中起始点不会出现变化，其服务器信息传输的起始点有且始终只有一个，为系统的客户服务器节点。如果分布式系统中所有服务器节点之间的通信传输能力都一致.那么不能把在同一位置，但信息请求的信息安全监控服务器时间不同，那么分布式处理服务器不能当作同一个，而是作为不同的分布式处理服务器对待[3]。在分布式系统中，服务器传输的通信量一定会低于物理链路所能承载的服务传输能力.且终止点始终为信息安全监控服务器节点，即终止点始终固定。

根据上述特征，将固定的起始点作为节点0，在分布式服务器运行中，节点0会在某个时段对n个服务器节点进行响应，服务器的点集表示为N=1，2，...，n，节点0向n个服务器节点发布任务，一直传输到安全监控服务器节点，即n+1，而所有分布式处理服务器节点的增加数量都用pi表示，i=1，2，...，n，且不容许拆分，当pi＞0，用bij来表示安全监控服务器节点和处理服务器节点群的相邻节点i和j。以不出现通道通信拥堵为大前提，则传输通道需要承载两大信息量，其一是客户服务器发送的信息外道通信，其二余下的信息量P（P≧pi），用V来表示所有由客户服务器节点发送的任务，V即为客户服务器节点的任务集合，下标则用k来表示。在这种安全设计架构中，信息安全监控服务器节点只依照客户服务器节点给出的任务进行监控。信息抵达监控服务器的时间用i表示，Min(i)表示信息到达安全监控服务器的最早时间窗，Max(i)表示信息到达安全监控服务器的最迟时间窗。

则其模型如下所示：

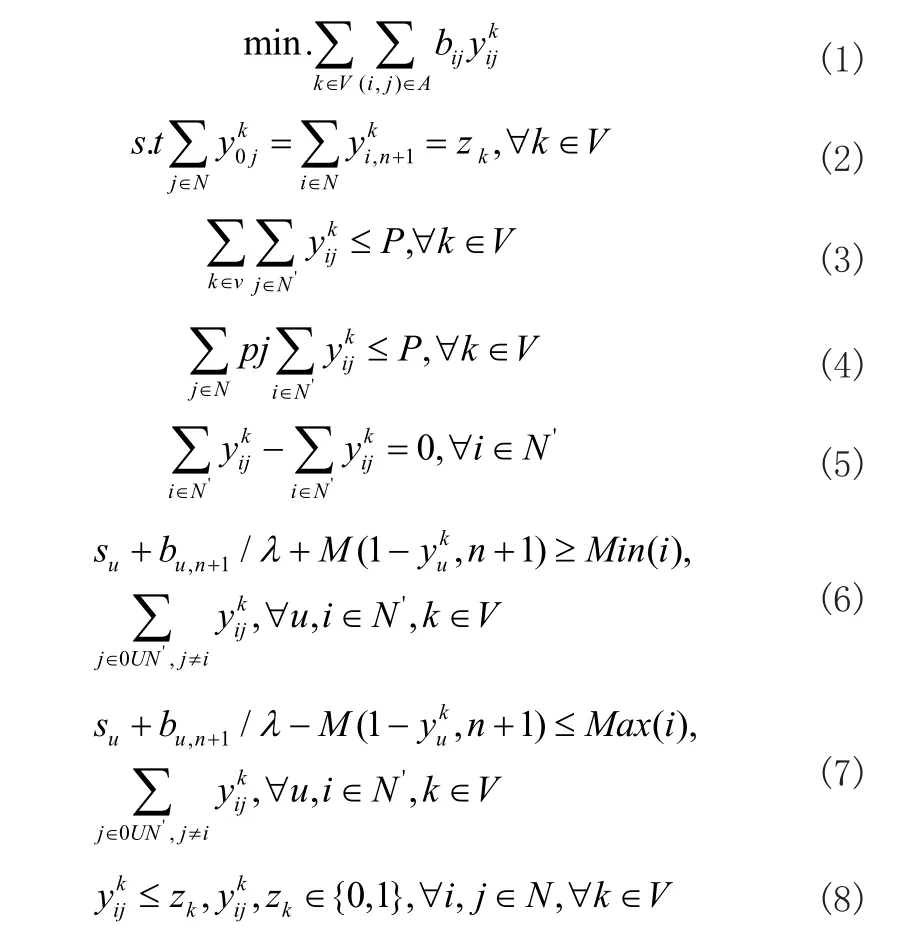
公式（1）到公式（8）是分布式系统结构的数据模型，公式（1）表示分布式系统在运行中需要达到的目标函数，公式（2）表示最小的通信路径，是确保客户服务器节点发出的信息能顺利到达信息安全监控服务器的关键，公式（3）是保证所有分布式处理服务器节点在进行信息传输时，信息的传输有且仅有一次，公式（4）是对传输通道除去客户服务器发送的信息外通信通道额外还能承载的信息量限制；公式（5）是对所有节点出入度平衡的保证，公式（6）和公式（7）是达到信息安全监控服务器的最早期望时间和最迟期望时间，公式（8）是0～1的变量逻辑关系。

3 启发式算法的设计

3.1 多节点增删线性规划处理

通信网络结构中都含有一个节点集V，而在这个节点集中又分别包括一个供应点集（VA）和需求点集（VB），其关系可表示为V={VA,VB}。由于通信网络中各个节点之间的逻辑关联相对固定，更改其传输通道后难以重建且造价非常高，因此一般情况下不可随意更改[4]。多节点连接控制一般使用线材或无线电磁波频率，为合理规划布置通信网络中的多个节点，应明确如式（1）所示的规划约束条件：

在以上约束式中，各参数意义如下：

C——线性规划求解结果

J——节点数

N——供应节点数

cj——j行的节点线性规划数量结果

利用式（1）的约束条件，可以分四步计算并确定节点增删位置和数量，相关步骤如下：

第一步：建矩阵，即建立权重和拓扑结构矩阵。我们用字母K代指约束关系中的常量。

第二步：确认节点数，初始化设置状态矢量，然后根据矢量判明整个通信网络节点集中存在的节点数量。

第三步：求解节点集，再引入Dijkstra（迪杰斯特拉）算法，对集合全部需求节点的最优路径进行计算，同时根据计算结果来建立需求节点的最优路径矩阵，算式如下：

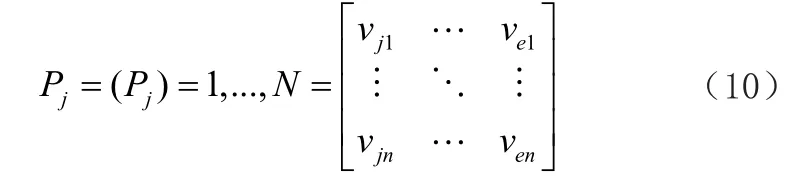
上式中各参数意义为：

Pj——多节点增删线性规划最优矩阵

vjn——起点最优路径长度

ven——终点的最优路径长度

利用建立的最优路径矩阵，在通信网络中任选一处节点并以其为中心点，结合得到的最优路径长度来找到符合条件的可达性需求点，并将这些点去除；其他的需求节点都归入到剩余集合中；将当前的供应节点作为起点，并对其可达性予以判定；按需增减或删除相关节点，由此实现对线性规划的增删处理[5]。

3.2 均衡分配多节点对应资源需求量

经过对多节点增删线性规划处理后，通信网络的全局节点布设也已初步完成，下一步工作的重心就是均衡配置，为实现更为理想的配置效率，必须首先保证多节点的对应资源需求量分配均衡，同时需要明确各节点传输距离间的最少耗时，以及相对应节点之间的路径耗时[6]。通信网络中可以借助网络传输路径来实现对多个节点的串联，然后可以使用商业数学软件MATLAB来增删优化整个通信网络结构中的节点。就近分配是通信网络中供应节点到需求节点的基本运行原则，整个通信网络相当于一个由众多子网络构成的分布式拓扑结构，各个子网络解耦中都配有一个基站，负责信号资源的收发处理。

3.3 多节点布局优化重配置

在不改变供应节点的前提下，根据需求节点对资源的实际需求量重新分配和连接优化，提高其布局合理性，进而实现对整个通信网络结构的优化处理。实际操作时，应充分结合通信网络的传输特性来重新考虑配置划分问题，首先，针对网络资源有限的情况，在不改变资源总量的情况下以优先满足需求节点的服务要求为根本目标，在最大成本限度内尽量保证单次资源配置的质量。按照这一配置方案可以尽可能地确保每个供应节点和需求节点的一一对应，从而改变供需节点配置不合理的现象。其次，需要在充分配置资源的基础上兼顾考虑资源的合理消耗问题。解决这类问题的关键在于对节点能力的把握，以现有的供应节点为条件，以降低配置成本为目标，按照每个供应节点的配置能力来合理配对需求节点，配置能力较强的供应节点可对应多个需求节点，由此保证服务质量和效率，实现对多节点的优化重配置。

4 结语

为了提高分布式环境下的信息量传输实时性和安全性，对具有实时性安全监控要求的分布式计算架构资源优化问题进行建模，然后通过启发式算法获得最优资源优化结果。该算法能在有效地保证系统实时性和安全性的基础上，将资源利用达到最优化，因此该设计思路在容量限制的通信环境下能对资源起到良好的优化效果，是提升分布式系统架构的最佳选择，适合在分布式环境中推广和应用。