基于新型核与灰度序列的时滞GM(1,N)模型及其应用
熊萍萍, 石 佳, 姚天祥, 闫书丽
(1.南京信息工程大学 管理工程学院,江苏 南京 210044; 2.南京信息工程大学 风险治理与应急管理研究院,江苏 南京 210044; 3.南京信息工程大学 数学与统计学院,江苏 南京 210044)
0 引言
些年来,雾霾作为我国较严重的一种空气污染问题,不仅对我国的自然环境造成了不良影响[1],而且对人类的身体健康也带来极大的负面作用[2]。因此,对雾霾进行准确的预测,对社会和人类而言意义重大。
国内外的众多研究人员为了更好地解决雾霾问题并进行有效防控和治理,建立了回归模型[3]、时间序列模型[4]、神经网络模型[5]等并对雾霾展开了预测分析。因为在雾霾期间的雾霾衡量指标以及因素变量数据都是以小数据特点展现出来,所以研究人员便通过灰色系统理论来探讨雾霾,得到预测精度较高的结果。Wu等[6]为了预测京津冀地区的空气质量数据,采用累加生成的阶数为分数的形式,构建预测模型;为了较准确地预测淮安市和南京市的空气质量,王志祥[7]和熊萍萍[8]等则采用GM(1,1)和MGM(1,m,N)模型。
灰色系统理论是一门新兴的学科,主要解决不确定性问题,它以贫信息、少数据建模为特点,对已有信息进行深入挖掘,进而探究不确定系统中的运行规律[9]。GM(1,1)模型是常见的一种预测模型,许多研究人员从多种视角对该模型进行改进[10~12],并在经、管、农、林、理、工、医等众多领域都有着广泛的应用。在GM(1,1)模型的基础上拓展可得到GM(1,N)模型,目前,对GM(1,N)模型的改进主要集中于背景值改进[13,14]、驱动项优化[15,16]、模型离散化[17,18]等方面。还有一些学者根据系统中存在的滞后性效应,对GM(1,N)模型[19,20]进行改进。
在对实验数据分析的过程中,往往不能用精确的数值来表达已存在的变动参数,这是因为外界原因会对数据的测量产生影响。所以这一区别于一般预测模型的灰色预测模型——在非精确数值区间建立模型被人们重视起来。曾波[21]和党耀国等[22]分别通过核和灰度序列、残差思想,针对区间灰数构建了GM(1,1)模型,石佳等[23]在核和灰度序列的基础上,引入线性时变参数,建立了GM(1,N)模型,上述优化模型是将实验数据中的实数范畴扩大到区间灰数范畴,以便于灰色模型在不同条件下的合理应用,使得灰色系统理论更加的完整且丰富。
在目前的实际应用过程中,原始GM(1,N)模型[24]只能适用于在同一时间下的变量,在建模的过程中没有过多地考虑时间滞后变化关系,因此常常在预测过程中产生或多或少的模拟预测偏差。本文将分析当期系统特征数据在往期相关因素作用下的滞后效应,在可能度函数为已知条件下,构建时滞GM(1,N)模型,并求解滞后参数。本文将会研究在大气污染物的影响下,雾霾可能受到的滞后影响,并将新构建的模型应用到南京市雾霾的模拟预测中。
1 基于新型核与灰度序列的时滞GM(1,N)模型的构建
1.1 建模机理
定义1设行为特征序列为:
与之对应的影响因素序列如下:
影响因素的第τi期时滞序列记为:

(1)
同理,基于新灰度序列建立的时滞GM(1,N)模型为:
(2)
特别地,当τi=0时,意味着行为特征序列与影响因素序列都处在同一时期,此时新型核与灰度的时滞GM(1,N)模型,退化为新型核与灰度的GM(1,N)模型。
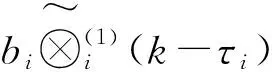

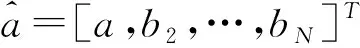
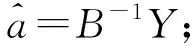
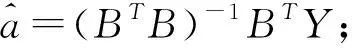
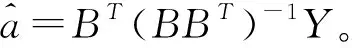
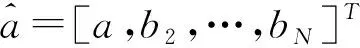
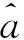
(1)白化方程
的解为:

(3)
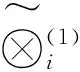
的近似时间响应式为:
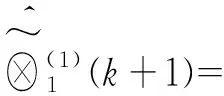
(4)

(3)累减还原式为:
(5)


(6)
其累减还原式为:
(7)
证明同定理2。
1.2 滞后参数τi的确定方法
为了提高模型预测精度,以新型核序列为例,给出新型核的时滞GM(1,N)模型关于滞后参数的目标函数:
(8)
同样地,可给出新型灰度序列的时滞GM(1,N)模型关于滞后参数的目标函数。利用MATLAB求解滞后参数,求出滞后参数τi的最优解之后,对模型中的结构参数进行辨识,最后,根据时间响应函数确定模拟值和预测值。
1.3 区间灰数上、下界的求解
根据下列方程组,求得每个区间灰数的上界及下界的模拟值和预测值[24]:
(9)
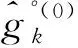
预测模型的好坏,其中一个重要的评价标准,就是模型的预测精度和预测效果。预测精度越高,则认为预测效果越好。在本文中规定,当平均相对误差控制在10%之内时,认为预测模型具有较好的预测效果,预测精度较高[25]。
2 实例分析
2.1 数据的选取与处理
PM10是一种粒径非常小的颗粒物,其粒径小于10微米,PM10浓度与NO2浓度密切相关[26],因此可以将NO2浓度选作PM10浓度的影响因素。本节将选择南京市2019年11月6日至11月21日的PM10浓度和NO2浓度展开探究剖析。
2.2 模型的建立与对比
11月6日~11月21日区间灰数的上下界确定规则如下:将11月4日至11月6日实际值的最高值和最低值作为11月6日对应区间灰数的上界和下界,根据对比,可以获得7日至21日相对应区间灰数的上下界。记PM10浓度的灰数序列为X1(⊗),NO2浓度的灰数序列为X2(⊗),取6~10日的数据为前期数据,11~17日为当期数据。各区间灰数的可能度函数由专家打分法求得,初始数据如表1所示。结合南京市近两年NO2浓度和PM10浓度的统计观测值,确定它们的论域为Ω1=Ω2∈[0,500]。
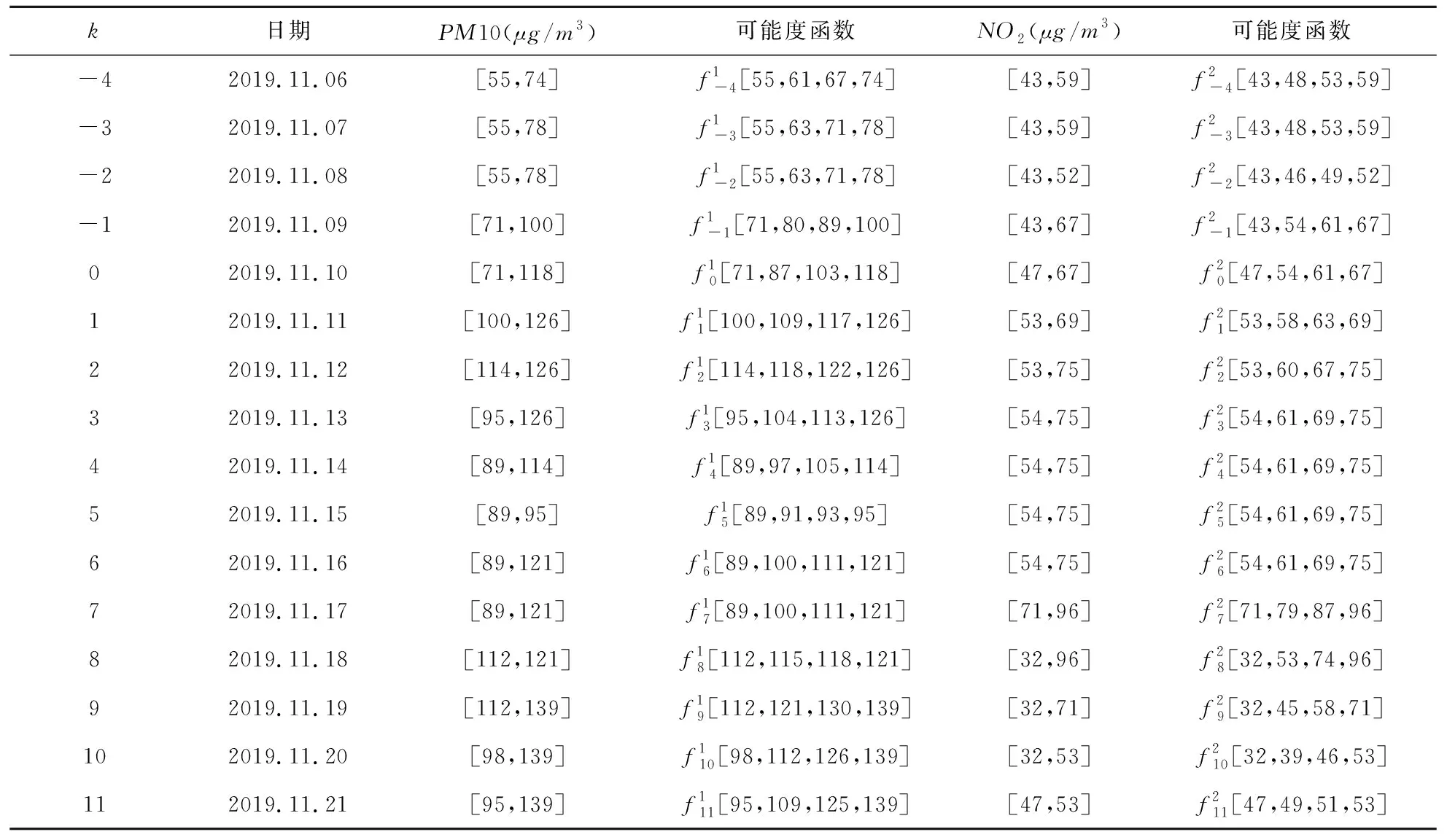
表1 PM10浓度、NO2浓度区间灰数及可能度函数
步骤1结合表1的数据,训练集选取2019年11月11日到17日的相关观测数据,测试集选取18日到21日的相关统计数据,根据新型核和灰度的计算公式,分别得到NO2和PM10浓度的核与灰度序列。
步骤2先后建立基于新型核和灰度序列的时滞GM(1,2)模型,利用滞后参数的求解方法,确定出两个模型中的滞后参数均为1。
步骤3构建PM10浓度关于新型核以及灰度序列的时滞GM(1,2)模型,可得到:
依据所得到的模型,计算出PM10浓度新型核以及灰度序列的模拟、预测值。
步骤4计算区间灰数的上、下界的模拟值和预测值,可直接由步骤3得到的PM10浓度新型核与灰度序列的模拟、预测值还原计算得出,具体结果详见表2和表3。
步骤5在步骤4的基础上,进一步计算对应的相对误差及平均相对误差,结果如表2和表3所示。本文通过比较一元回归模型和新构建的时滞GM(1,2)模型,以此验证本文所提出模型的有效性和适用性,两个模型的相关结果详见表2、表3所示。
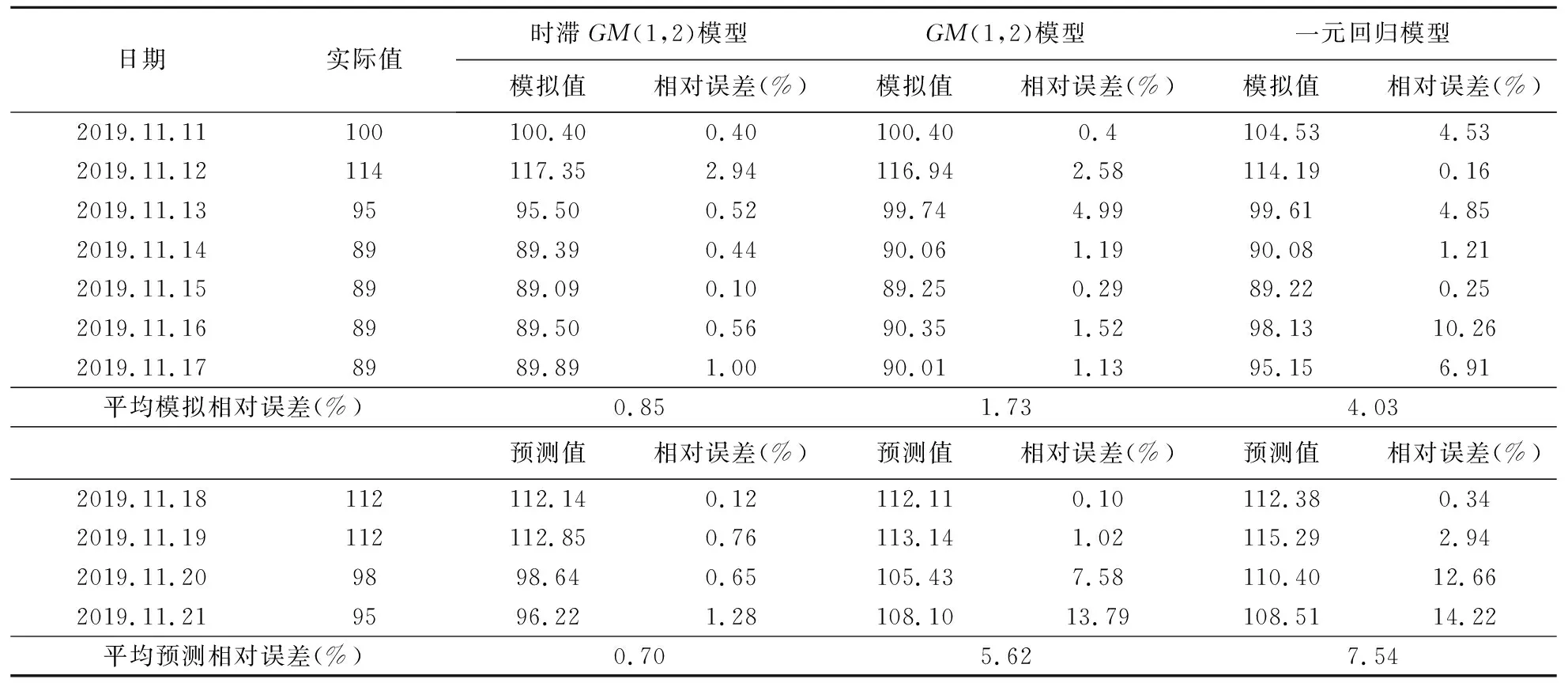
表2 PM10浓度区间灰数的下界模拟预测值及相对误差

表3 PM10浓度区间灰数的上界模拟预测值及平均相对误差
为了更清晰地对比基于新型核与灰度序列的时滞GM(1,2)模型和GM(1,2)模型、一元回归模型的结果,结合表2、和表3的数据,可以画出PM10浓度上下界相对误差对比图,如图1、图2所示。

图1 PM10浓度下界相对误差

图2 PM10浓度上界相对误差
从表2与表3的数据中可以发现,文中提出的优化时滞预测模型适用于处理具有时滞特征的小数据、贫信息的不确定系统问题。从模拟值来看,对比一元回归模型5%左右的上、下界平均相对误差,本文所提出的时滞GM(1,2)模型和传统的GM(1,2)模型的平均相对误差更低,均处于2%以下。从预测值来看,本文提出的时滞模型GM(1,2)相较于传统GM(1,2)模型和一元回归模型,上、下界的平均相对误差前者明显均低于后两个模型,为3.46%。这主要是由于后两个模型未将NO2浓度与PM10浓度之间的时滞效应考虑在内而导致相对误差偏大。基于以上分析,本文提出的在新型核与灰度基础上建立的时滞GM(1,2)模型,由于将大气污染物浓度之间存在的滞后关系考虑进来,所以能够降低传统GM(1,2)模型的平均相对误差,提升预测效果。
3 结论
本文在对滞后参数的识别和对模型机理的探索过程中,将影响因素的滞后特征考虑在内,建立了基于新型核与灰度的时滞GM(1,2)模型。在已给出可能度函数的情形下,将滞后参数引入到传统GM(1,N)模型的驱动项中,得到本文所提出的优化模型。该模型在计算、应用过程以及计算机操作中都具有较强优势,不仅可以对小数据样本进行处理,还能解决因素变量的滞后效应带来的相关问题。通过案例实证,结果显示:在考虑南京市PM10浓度与NO2浓度的滞后关系后,模型对污染物浓度的预测精度更高,高达96%以上。由此可见,本文提出的考虑了相关因素滞后影响的新模型进一步完善了灰色预测模型,并拓展了其应用范围。

