GA-ACO算法优化BP神经网络的重型车排放预测

闻增佳,谭建伟，王怀宇，余 浩，常 虹，孙文强

(1.北京理工大学 机械与车辆学院， 北京 100081； 2.中国汽车工程研究院股份有限公司， 重庆 401122；3.潍柴动力股份有限公司OBD标定室， 山东 潍坊 261001)

0 引言

2020年，全国机动车保有量达到3.72亿辆，全国机动车四项污染物(CO、HC、NOx、PM)排放总量已达到1 593.0 t，机动车污染物的排放成为环境大气污染的重要源头[1]。为了更有效地减轻重型车污染物排放造成的危害，全球各国已经付出了长达数十年的努力，目前建立了以欧盟、美国和日本为代表的3种重要排放标准体系[2]。标准体系对于重型车排放物的检测大多依靠实验室的特定测试循环，而部分研究也表明受实际道路状况影响，对重型车的实验室测试循环并没有真实反映实际道路的污染情况，实际道路的重型车排放污染物被明显忽视[3]。将便携式排放测试系统(PEMS)运用于机动车的尾气排放检测的技术得到了迅速发展，能真实反映实际道路的排放量[4]。因此建立一种用于重型车污染物的排放预测模型，不仅能有效减少试验耗时，还能降低多次重复RDE试验带来的经济支出。

国内外学者针对机动车污染物的排放预测进行了系列研究，提出了多种排放预测的方法与改进措施。周斌等[5]尝试抛开传统数学模型，把神经网络技术引入对内燃机的排放特性预测，结果表明，神经网络的预测精度并不依赖于实际情况的数学模型，证明了该方式的可行性；Yap等[6]建立了常见的前馈神经网络发动机排放预测模型，通过调整输入条件与隐含层节点数确定多层前馈神经网络的预测误差最低，应用价值最高；文华等[7]开发了一种针对柴油机NOx瞬态排放预测研究的方法，采用遗传算法优化网络权值的BP神经网络，结果表明神经网络泛化能力较好，精度较高；王志红等[8]构建了一种针对重型车道路污染特征的预测模型，通过使用Levenberg-Marquardt算法优化了双隐含层BP神经网络，用遗传算法调整网络的权值与阈值，该模型对车辆的瞬时排放和整体排放特征有较好预测。

神经网络模型具有技术发展成熟、开发耗时短、开发成本低廉和预测精度较高等优点。基于此，本文在遗传算法优化BP神经网络权值和阈值的基础上，通过蚁群算法进一步提高神经网络寻找最优解的精度，利用PEMS设备测得的符合国Ⅵ标准的RDE试验测试数据，建立用于重型车的排放预测模型。

1 RDE试验方案

1.1 试验车辆

试验车辆为某辆符合国Ⅵ标准的重型车，RDE试验准备前将车辆装至满载状态，试验车辆信息如表1所示。

表1 试验车辆信息

1.2 试验设备

PEMS系统主要使用日本HORIBA公司开发的OBS-ONE车载尾气分析系统，系统主要由气态污染物检测模块、颗粒物检测模块、排气流量计、数据通讯系统、全球定位系统(GPS)、气象站构成，能够即时测量车辆尾气中一氧化碳(CO)、二氧化碳(CO2) 、氮氧化物(NOx)、颗粒物数量(PN)的含量，同时可以测量车辆的排气流量，掌握车辆行驶状态、车辆位置信息以及车辆所处的外界环境参数。PEMS系统使用外置电源，排气量计与排气管连接后固定安装在车辆尾气出口，GPS和气象站安装在车头，气态污染物检测模块和颗粒物检测模块固定在车头内部，具体安装布置情况如图1所示[3]。

①OBD通讯连接；②温、湿度传感器；③GPS排气流量计；④急停按钮；⑤控制电脑；⑥排气流量计；⑦颗粒物检测模块；⑧气态物检测模块；⑨外接电池；⑩负载

1.3 试验要求

参照重型车国六排放标准的测试规程[9]，RDE试验按照市区、市郊和高速工况依次完成，其中市郊工况允许短时出现市区工况，而高速工况则允许短时出现市区和市郊工况。根据车型3种工况构成要求不同，由实际行驶时间确定工况占比，具体参数见表2。RDE试验除在行驶工况分配占比和行驶车速大小要求外，须符合2～38 ℃的环境温度要求，同时须符合海拔高度条件，试验时海拔不超过1 000 m(相当于大气压90 kPa)。试验起始点和结束点的海拔高度差应小于100 m，试验车辆累计正海拔高度差增加量应小于1 200 m/100 km。

表2 PEMS试验工况参数

2 排放预测模型的建立

2.1 试验数据前处理

对试验流程中记录的污染物浓度、车辆运行数据、车辆环境参数及其他瞬态信息进行时序校正，时序校正后需要剔除数据中的无效数据，其中包括PEMS设备检查和零点漂移核查过程的数据；发动机冷启动即发动机点火后冷却液温度超过70 ℃期间或冷却液温度5 min内改变小于2 ℃期间的数据等[9]。

在筛选所有无效数据后，选取了6 000组有效样本数据。为避免模型出现过拟合问题，提高建立模型的泛化水平[10]，保证样本训练集占绝大部分，将所有样本数据随机划分为3部分：训练集80%、测试集15%、验证集5%。

2.2 输入参数提取

输入参数的选择对于预测模型的性能有着很大的影响，样本中输入参数过多或数据量级差别过大会导致模型预测时间过长且精度降低，因此选择的输入参数应与所预测输出值相关性较高，选取对结果影响较为明显的输入参数可以明显提高神经网络模型对结果预测的精度与准度[11]。输入参数的选择还应考虑参数实际试验获取数据的可行性，实际测试过程中受多种条件制约，可测量的参数可能较为有限。

考虑到影响排放结果的因素较多，采用灰色度关联算法模型进行参数提取，降低样本维度。灰色关联度算法分析通过反映两序列间发展过程的相近性或发展趋势的相似性来构造关联度[12]。相对于只考虑相似性的绝对关联度和只考虑相近性的邓氏关联度，同时兼顾相近性与相似性的B型关联度算法更加科学、合理[13]。样本数据的随机分组也可弥补B型关联度算法不具备保序性的缺点。

设参考序列为:X0={x0(k),k=1,2,…,n},设Xi={xi(k),k=1,2,…,n}(i=1,2,…,m)为被比较序列(因素序列)。

同时令：

(1)

(2)

(3)

(4)

本文主要研究的是重型车的排放预测结果，所以选择的输入参数必须是与输出值NOx特性密切相关的参数。初步选定输入参数的范围后，使用B型关联度来评估输入参数与输出值的关联度，各输入参数与输出值的B型关联度值如图2所示，评估结果的数值越大，表明输入参数对输出值的影响越显著。

图2 不同参数的B型关联度曲线

使用影响较为显著的发动机转速、车速、车辆加速度、比功率、燃油消耗值、排气流量、排气温度作为神经网络模型的输入参数。发动机转速变化会使车辆速度、加速度变化，而车速、加速度和比功率对排放有显著的影响，排气温度、排气流量能反应燃烧情况，燃油消耗值能计算燃烧产物，均可反映排放情况。

车辆的比功率(vehicle specific power,VSP)代表机动车发动机每移动1 t质量(包含自重)所输出的功率[14]，其计算式如下：

VSP=v[1.1a+9.81arctan(sing)+0.132]+

0.000 302v3

(5)

其中：v为速度；a为加速度；g为道路坡度，无量纲。

因为实际道路测试过程中的测试道路坡度变化并不明显，故不考虑道路坡度对VSP的计算影响，g取值为0，因此，表达式可以简化为：

VSP=v[1.1a+0.132]+0.000 302v3

(6)

2.3 神经网络架构

BP神经网络是一个多层前馈的神经网络，作为目前使用最为普遍的神经网络预测模型之一，拥有强大的非线性映射能力和高度柔性的网络结构[15]。其结构如图3所示。

图3中，X=(x1,x2,…,xn)T为输入层；Y=(y1,y2,…,yn)T为隐含层，隐含层的数目可根据研究问题进行相应调整；Z=(z1,z2,…,zn)T为输出层；V、W分别为各层间的权值。

尽管BP神经网络的理论和性能方面都已较为完善，但它仍然具有不少缺陷：学习速度慢、迭代耗时过长、易陷入局部最小值等，上述缺点都影响着BP神经网络预测结果的准确性。

图3 三层BP神经网络结构示意图

2.3.1遗传优化算法

遗传算法用来优化BP神经网络的初始权值和阈值，将经过优化的权值和阈值代入BP神经网络可以得到更好的预测结果。具体步骤如下[16]：

1) 编码。即将需要优化问题的解转换为遗传算法可以解决的空间搜索的转换方法。

2) 初始化种群。

3) 适应度函数。适应度函数设为输出预测值与输出期望值之间的误差绝对值，计算式为：

(7)

其中：F为适应度值；h为量纲为一系数；n为节点数；yi和oi分别为第i个节点的输出期望值和输出预测值。

4) 选择操作。选择操作模拟在遗传进化过程中生物种群个体完成自然淘汰的过程，本文使用轮盘赌法作为选择算子，其概率计算式为：

(8)

其中：pi为个体的适应度值；u为量纲为一系数；Q为种群的个体总数。

5) 交叉操作。指模拟生物群体在进化过程中，通过交配重组部分基因而形成新生个体的过程，本文采用两点交叉作为交叉算子。

6) 变异操作。指模拟生物群体内在的遗传发展过程中，由于产生基因突变而形成新生个体的过程。本文采用高斯变异作为变异算子。因为高斯分布的特性使算法在可以解除局部约束的同时，又具备了局部搜索功能。

通过遗传算法完成上述步骤后得到了优化后的权值和阈值并代入BP神经网络，开始进行预测。

2.3.2蚁群算法

蚁群算法是一种用来寻优路径的概率性算法[17]， 原理的灵感来源于蚂蚁在寻找食物过程中选择路径的行为，即蚂蚁先在搜寻食物的路线上释放信息素，再从最初遇到的分叉路口随机地选定前进方向，同时释放与路径长度相关的信息素，信息素含量与路径长短成反比，当重复遇到相同路口选择信息素含量更高的路线，在正反馈的机制作用下最终获得信息素含量最高的最优寻食路线。算法实现的具体步骤如下[18]：

1) 初始化蚁群参数。

2) 蚁群移动规则确定。蚂蚁移动规则选用随机比例原则，假设城市节点数为m，人工蚁群蚂蚁数目为n，dij=(1,2,…,m)表示从城市节点i到城市节点j之间的路程，计算公式为[19]：

(9)

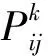
3) 信息素更新。对信息素浓度进行更新处理，其计算式为：

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(10)

其中：ρ为信息素挥发因子，ρ∈(0,1)；Δτij(t)表示蚂蚁k在当次循环下留在城市节点i与城市节点j连接路径上的信息素增量[21]，表达式为：

(11)

2.3.3蚁群遗传混合算法

遗传算法可以在大范围内快速进行搜索，但对于反馈信息的利用较弱，所以求解运算一定时间后会出现大量重复迭代，使得算法优化效率降低；而蚁群算法由于蚂蚁个体的独立性，采用分布式并行计算，同时信息素的使用具有正反馈的特点，能够有效利用系统反馈信息，但求解前期由于缺乏信息素，导致求解缓慢。将遗传算法与蚁群算法优势互补，混合后可以提高单一算法的优化效率。前期使用遗传算法确定的最佳信息素，利用最佳信息素更新蚁群算法确定初始信息素，最终得到GA-ACO混合算法优化的BP神经网络流程如图4所示。

图4 GA-ACO混合算法优化的BP神经网络的流程框图

3 预测结果分析

使用建立完成的基于GA-ACO混合算法优化BP神经网络的排放预测模型，对选取的重型车NOx排放进行训练与预测。

使用的训练集的NOx排放因子分布情况如图5所示，其中NOx集中分布在0～0.04 g/s，占比约89.5%，排放因子大于0.06 g/s的样本约占总数据样本的3.7%。

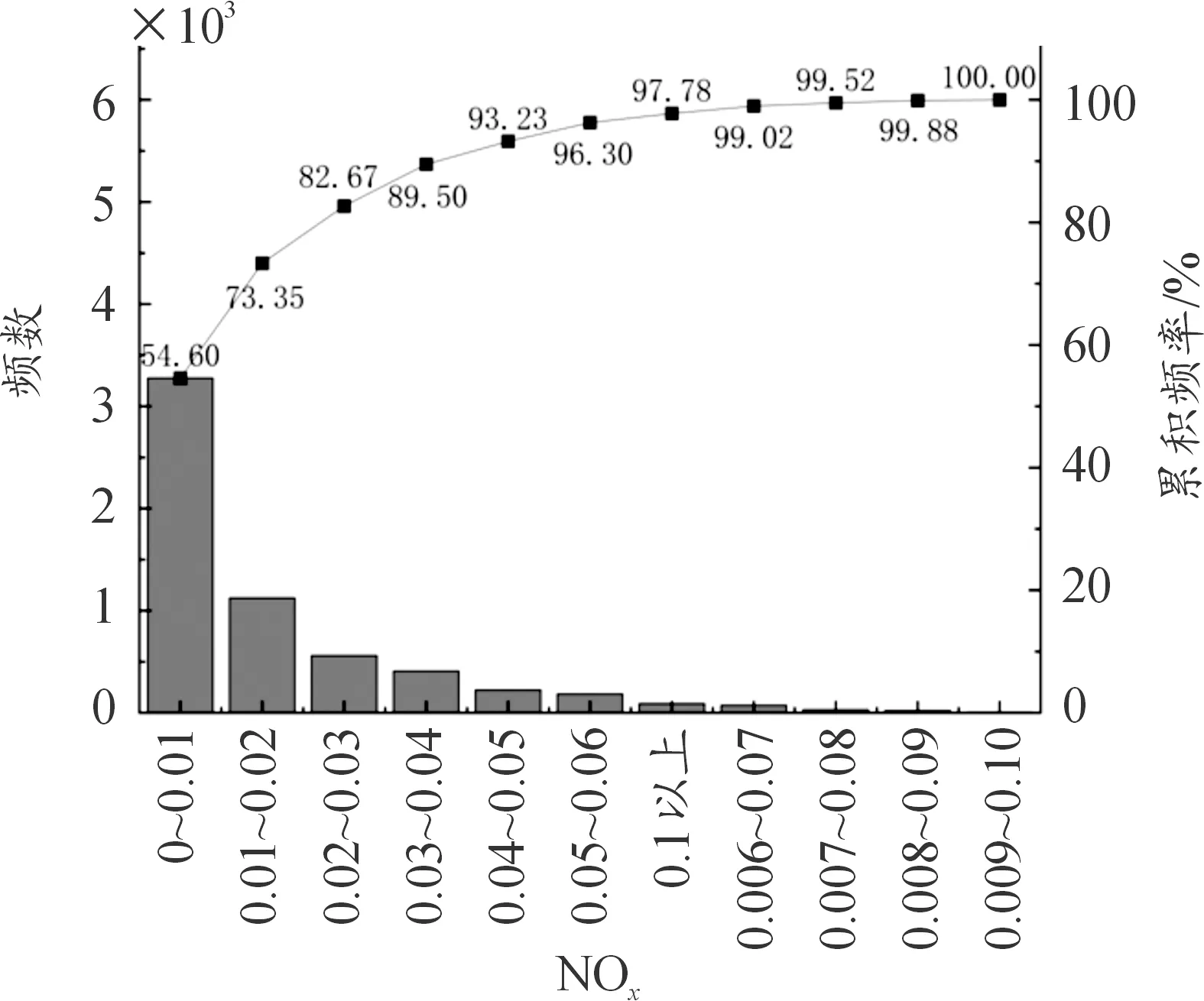
图5 NOx排放因子分布图

如图6，可以看到在23、79、158、187、228等点位附近有明显的误差出现，BP神经网络模型在较大峰值处未能很好响应，预测值普遍小于实测值。

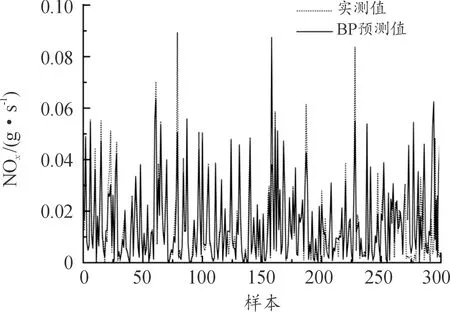
图6 BP预测NOx值和实测值曲线

对比图6和图7可以发现，经过GA-ACO优化的BP神经网络对NOx的预测在有明显误差的点位都能显著优化，在预测结果与实际样本的波峰、波谷附近，尤其是NOx实测值较大的预测点位附近，出现了较明显的偏差。误差产生的原因一方面是由于运行工况的剧烈变化，模型的响应情况较差：由于神经网络训练过程中，对于权值与阈值的优化主要用以衡量整体误差大小。而由图5可知，NOx排放因子的分布主要集中于0～0.04 g/s，大量的小值和少量的高峰值使得峰值部分的预测结果普遍小于实测值。另一方面原因是模型未将后处理系统纳入考量之中：在发动机充分暖机完成前，后处理装置温度不够，无法有效对尾气中的NOx进行还原；车辆在行驶过程中频繁起停，排气温度较低且波动明显，使得后处理无法维持良好反应条件；同时车辆在行驶过程中，较为频繁的加减速，尤其是在急加速时，排气流量和排气流速迅速增大，后处理装置因为流速增大导致反应时间较短，大量未被还原的NOx随尾气排出等。

图7 GA-ACO-BP预测NOx值和实测值曲线

综上，模型由于工况的激烈变动以及未考虑后处理装置产生较大误差。预测时产生的误差与神经网络模型忽略试验风速、海拔高度、场地温湿度等因素是否有关仍有待后续研究证实。但由于根据B型关联度选择了对NOx排放因子影响显著的排气流量、燃油消耗值等，模型预测结果的整体趋势与实际排放的整体趋势相近，可以认为模型的预测值与样本值能较好吻合。

为了进一步评估模型瞬时预测的准确性，选择使用能够表达2种数据变量的直接相关程度的皮尔逊相关系数进行分析，皮尔逊相关系数r的计算公式如下：

(12)

其中：Xi为实际排放值；Yi为预测排放值。

通常情况下，皮尔逊相关系数划分为：0.7≤|r|<1表示线性高度相关；0.4≤|r|<0.7表示显著性相关；|r|<0.4表示相关性较弱；r=1表示完全正相关，r=0表示无关，r=-1表示完全负相关。

BP模型对NOx预测的皮尔逊相关系数为0.932 7，GA-ACO-BP模型对NOx预测的皮尔逊相关系数为0.9686，因此可以认为引入GA-ACO算法对排放模型的瞬时预测有明显优化，同时可以认为所建立的GA-ACO-BP排放预测模型对重型车瞬时排放有较高精度的预测。

将整个实际运行工况按照市区、市郊和高速3种工况划分，分别对3种工况的NOx的排放情况进行训练与预测，计算3个工况的NOx排放因子，用以评估预测模型的总体排放误差情况，其结果如表3所示。可以看到，GA-ACO-BP模型所得NOx排放因子的最大相对误差为2.36%，小于BP模型最小相对误差的3.46%，可以认为GA-ACO算法对排放模型的总体预测有明显优化。同时由于运行工况的剧烈变化，权值与阈值优化优先满足整体误差，波峰处预测值普遍小于实测值，使得3个工况和全程均是预测值小于实测值。观察计算结果，可以发现误差大小都在可接受范围内，可以认为所建立的GA-ACO优化BP神经网络的排放预测模型能够对重型车整体排放有较好预测性。

表3 NOx排放因子预测误差

4 结论

1) GA-ACO-BP模型使用B型关联度选择RDE试验数据中的主要成分作为模型输入，其中排气流量、燃油消耗值等对排放因子预测影响较为明显。

2) GA-ACO-BP模型对NOx的预测结果与样本数据的皮尔逊相关系数由BP模型的0.932 7提高到0.968 6，线性高度相关。说明GA-ACO-BP模型对重型车瞬时排放预测准确性较高。

3)GA-ACO-BP模型对市区、市郊、高速3种工况进行预测，预测结果由BP模型的最小相对误差3.46%提高到最大相对误差不超过2.36%。说明GA-ACO-BP模型对重型车的整体排放有较好预测性。