基于自适应遗传算法的随机森林模型参数优化方法

蔡 明，孙 杰，杨维发，鲍 清，李培德

（1 湖北省气象信息与技术保障中心，武汉 430074；2 中国气象局武汉暴雨研究所暴雨监测预警湖北重点实验室，武汉 430074）

0 引言

随机森林回归（Random Forest Regression）算法作为一种灵活且易于使用的机器学习算法［1-2］，其理论和方法已被作为一种替代一般线性模型（线性回归、方差分析等）和广义线性模型（逻辑斯蒂回归、泊松回归等）的方法，广泛应用于工程应用和科学领域中复杂问题的解决上。国内外学者对随机森林在回归和分类问题中的应用进行了全面研究。在国外，Kulkarni 等人［3-4］为了提高分类正确率，将决策树维度分为2 部分。Oshiro 等人［5］证明了在随机森林性能达到最优时决策树数目存在临界值。Bernard 等人［6］研究了随机森林强度与相关性的关系。在国内，袁远等人［7］利用随机森林算法对非线性数据特征的学习能力，优化ARIMA 模型预测残差，最终达到提高回归预测精度的目的。马景义等人［8］综合了Adaboost 算法和随机森林算法的优势，提出了拟自适应分类随机森林算法。冯开平等人［9］将加权K 最近邻法（KNN）与随机森林算法结合应用于表情识别，简化了计算复杂度的同时取得了不错的识别率。

自适应遗传算法是将生物进化论的自然选择和遗传机理应用于粒子滤波算法以克服其粒子多样性退化不足的一种随机化搜索方法［10-11］。其主要特点是按照优势种群遗传的原则将粒子适应度变化情况作为遗传操作中交叉和变异概率变化的依据，通过对粒子的选择、交叉和变异操作模拟生物界优胜劣汰、适者生存的过程，由于其直接对结构化的对象进行操作，故具有很好的全局寻优能力。但是由于遗传操作中的交叉和变异概率是预先设定的，参数选取不当容易使算法陷入局部最优［12-15］。

基于以上研究论述，本文提出一种基于自适应遗传算法的随机森林回归模型参数优化方法，使用Boston house price 数据集对经过该方法优化后随机森林模型的回归预测效果进行验证。

1 相关算法介绍

1.1 随机森林回归算法

随机森林回归（Random Forest Regression，RFR）算法是一种基于决策树（Decision Tree）的引入随机特征选择的Bagging 类集成算法，目前被广泛应用于各类回归问题。本文使用Boston house price 数据集对随机森林回归模型进行训练和预测。随机森林回归模型的建立过程如下：

（1）从原始训练集中使用bootstrap 方法随机有放回采样取出m个样本，共进行n_tree次采样。生成n_tree个训练集。

（2）对n_tree个训练集，分别独立训练n_tree个决策树模型。

（3）对于单个决策树模型，假设训练样本特征个数为n，选择最好的特征进行切分。

（4）每棵树都按照步骤（3）来切分下去，直到该节点的所有训练样例都属于同一类。在决策树的切分过程中不需要剪枝。

（5）将生成的多棵决策树组成随机森林，模型最终预测结果为随机森林中多棵决策树预测结果的均值。

决策树的生长过程就是使用满足划分准则的特征不断将数据集划分为纯度更高、不确定性更小的子集的过程。

在步骤（3）中，当训练决策树模型时需要考虑怎样选择切分特征、切分点以及怎样衡量切分特征、切分点的好坏。针对切分特征和切分点的选择，本文采用穷举法，即遍历每个特征和每个特征的所有取值，再从中找出最好的切分变量和切分点；针对于切分特征和切分点的好坏，一般以切分后节点的不纯度来衡量，即各个子节点不纯度的加权和G（xi，vij），其计算公式如下：

其中，xi为节点的某一个切分特征；vij为切分特征的一个切分值；nleft、nright、Ns分别为切分后左子节点训练样本个数、右子节点训练样本个数以及当前节点所有训练样本个数；Xleft、Xright分为左、右子节点的训练样本集合；H（X）为节点的不纯度函数（impurity function），回归模型一般采用均方误差（Mean Square Error，MSE）或平均绝对误差（Mean Absolute Error，MAE）作为不纯度函数，本文则选用了MSE作为模型的不纯度函数，其数学定义公式见式（2）：

其中，Xs为当前节点训练样本集合；ns为当前节点训练样本数目；为当前节点样本目标特征的均值。

将式（2）带入式（1）后，对于任意切分点可以得到：

1.2 自适应遗传算法

以往的遗传算法常使用恒定不变的概率对粒子进行交叉和变异等遗传操作，这样会导致粒子群中适应度较大的优势粒子容易被丢弃掉，同时新的优势粒子也不容易产生，致使算法一旦陷入局部最优，就很难跳出。

针对这一问题，提出一种基于生物遗传进化思想的自适应遗传算法（AGA）。算法中，高适应度的优势个体以较高概率进行交叉操作，这样可以增大优势基因遗传到子代的可能性，更符合遗传进化规律；低适应度的个体以较高的概率进行变异操作，这样就更容易通过变异操作产生新的优势个体，避免算法陷入局部最优。通过自适应地调节遗传操作中的交叉、变异概率，从而避免遗传算法中早熟现象的出现。其中，遗传操作的交叉概率Pc和变异概率Pm可以分别表示为：

1.3 基于自适应遗传算法的随机森林回归参数优化

以往的随机森林回归算法的参数优化多通过绘制学习曲线或网格搜索交叉验证的方法实现，实施过程中恒定不变的搜索步长使得最优参数的获取很难在速度和效果上同时达到最优。基于此，提出自适应遗传算法辅助下的随机森林回归模型参数优化方法，利用遗传算法优异的全局寻优能力，结合自适应方法动态调整的遗传操作概率，达到快速取得全局最优解的目的。

随机森林回归是基于bagging 框架的决策树模型，因此随机森林回归模型的参数调整包括2 部分：随机森林框架的参数调优和决策树的参数调优。使用自适应遗传算法进行随机森林回归模型参数优化的流程如图1 所示。

图1 基于自适应遗传算法的随机森林回归模型流程图Fig. 1 Flow chart of Random Forest regression model based on adaptive genetic algorithm

2 实验准备

2.1 数据集准备

为了验证经自适应遗传算法优化后的随机森林回归模型的有效性，使用Kaggle Boston house price数据集进行仿真验证。数据集中的每一行数据都是对波士顿周边或城镇房价的情况描述，数据集共有14 个特征，分别为：城镇人均犯罪率（CRIM）、住宅用地所占比例（ZN）、城镇中非住宅用地所占比例（INDUS）、虚拟变量（CHAS），用于回归分析；环保指数（NOX）、每栋住宅的房间数（RM）、1940 年以前建成的自住单位的比例（AGE）、距离5 个波士顿就业中心的加权距离（DIS）、距离高速公路的便利指数（RAD）、每一万美元的不动产税率（TAX）、城镇中的教师／学生比例（PTRATIO）、城镇中的黑人比例（B）、地区中有多少房东属于低收入人群（LSTAT）、自住房屋房价（PRICE）。其中，PRICE为目标变量，其他13 个特征为模型的输入自变量特征。各自变量特征的重要性见表1。由表1 可以发现，不论是RFR 模型、还是自适应遗传算法优化后的AGA -RFR 算法模型，各自变量的重要性程度都是相近的，且RM和LASTAT都是对模型最重要的变量。

表1 模型特征变量重要性Tab.1 Importance of model characteristic variables

模型初始特征集中各项特征之间的相关性热力图如图2 所示。图2 中，部分特征间呈现负相关性，部分呈现正相关性。将Kaggle Boston house price 数据集按照7 ∶3 的比列划分为训练集和测试集。

图2 模型特征相关性热力图Fig. 2 Model characteristic correlation thermodynamic diagram

2.2 评价指标

为了对比自适应遗传算法参数优化方法的应用对随机森林回归模型预测精度的影响，需要对随机森林回归模型的预测精度进行评价。本文使用均方根误差、决定系数和平均绝对误差这3 个指标对模型的预测精度进行评价。对此拟给出研究分述如下。

（1）均方根误差（Root Mean Squared Error，RMSE），也叫回归系统的拟合标准差。由于均方根误差对一组测量值中的特大或特小误差反映非常敏感，所以，均方根误差能够很好地反映出测量的精密度。具体数学公式可写为：

（2）决定系数（Coefficient of Determination，R2）。表示对模型进行线性回归后，评价回归模型系数的拟合优度。R2反映了模型因变量的全部变异能通过回归模型被自变量解释的比例。R2越大，线性回归模型解释的变异越大。具体数学公式可写为：

R2为1 时，表明模型预测值和真实值观测值没有任何误差，表示回归分析中自变量对因变量的解释越好；R2为0 时，模型中样本的每项预测值都等于均值；R2接近于0 时，表明模型预测能力差，预测效果接近于“使用观测值的平均值作为模型预测值”。这就表示可能用了错误模型，或者模型假设不合理。

（3）平均绝对误差（Mean Absolute Error，MAE）计算公式如下：

其中，MAE的取值范围为 [0，＋∞），当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

3 结果与分析

研究使用Kaggle Boston house price 训练数据集对经过自适应遗传算法优化得到的随机森林回归模型进行训练，训练后的模型对测试集进行预测。对比未经过参数优化的RFR 模型与经过参数优化的AGA-RFR模型的预测结果，预测效果对比见表2。

表2 模型预测精度对比Tab.2 Comparison of prediction accuracy of models

观察表2 可以发现，经过自适应遗传算法优化参数后的AGA-RFR 模型的回归预测结果中，RMSE为4.111，优于RFR 的4.174；AGA-RFR 的R2为0.868，同样优于RFR 的0.833；对比2 种模型的MAE也是同样的情况。综上可知，经过参数优化后的AGA-RFR 模型的MAE要优于RFR 模型。这就说明通过使用自适应遗传算法对随机森林回归模型的参数进行优化，使得随机森林回归模型的预测效果得到了提高。

以Prices为横坐标，Predicted prices为纵坐标，绘制出的模型预测价格与实际价格的对比结果图如图3 所示。

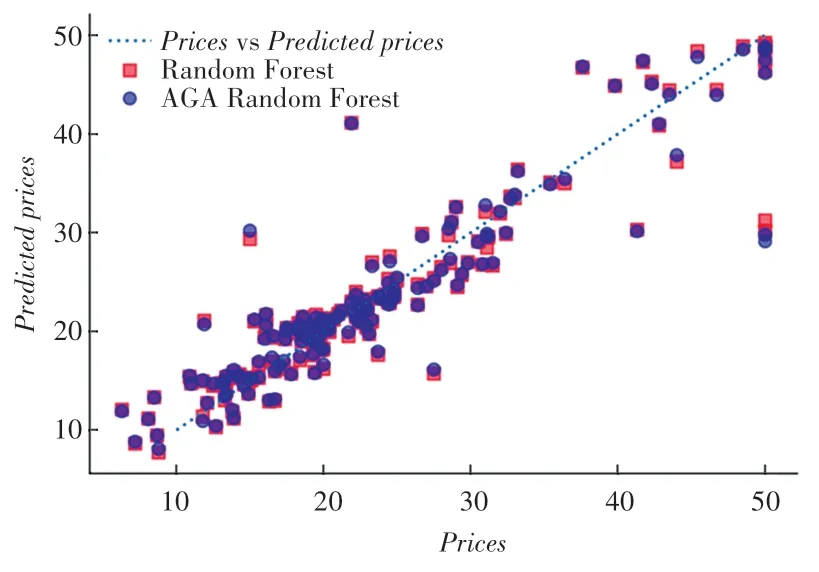
图3 模型预测价格与实际价格对比图Fig. 3 Comparison between model predicted prices and actual prices

由图3 可知，相比于方形所代表的RFR 模型预测结果，圆形所代表的AGA-RFR 模型的预测结果总体上更接近于代表模型预测价格与实际价格相等的虚直线。由此说明，AGA-RFR 模型的预测结果比RFR 模型的预测结果更接近于真实价格。

模型预测值残差与实际价格对比如图4 所示。图4 中，相比于方形所代表的RFR 模型预测结果，圆形所代表的AGA-RFR 模型的预测结果总体上更接近于代表预测残差为0 的虚直线。这也说明，AGA-RFR 模型的预测结果比RFR 模型的预测结果具有更小的预测残差。

图4 模型预测值残差与实际价格对比图Fig. 4 Comparison between residual error of model predicted value and actual prices

4 结束语

本文提出一种用于随机森林回归模型参数优化的方法，利用自适应遗传算法在求解全局最优解的研究时不易陷入局部最优的优势，通过对粒子的选择、交叉和变异操作模拟生物界优胜劣汰、适者生存的过程。通过使用Boston house price 数据集对经过该方法优化后随机森林模型的回归预测效果进行验证，试验结果表明，经过该方法参数优化后的AGARFR 模型的回归预测效果要优于未经过参数优化的RFR 模型的预测效果。

本文提出的基于自适应遗传算法的随机森林模型参数优化方法可以作为随机森林回归模型参数优化的一种有效手段。