基于偏振降噪的分布式光纤振动定位算法研究
高擎昊,苏幸晨,张成龙,吕立冬
(安徽工业大学电气与信息工程学院,安徽马鞍山 243032)
0 引言
由于管道运输运量大、安全性好、连续性强、经济性高,需要持续供应的资源大多通过管道运输。针对管道破坏事件,分布式光纤振动传感技术凭借其优势可以满足对周界安防长距离、高空间分辨率的监测需求[1]。
与常规传感方案相比,分布式光纤振动传感系统使用光纤作为传感媒介,代替点式电子式传感器和相关导线,可用于建筑内部裂缝检测、管道安防监测。Y. L. Lu等[2]基于相敏光时域反射技术,采用相干探测方式,结合移动平均、移动差分信号处理算法,设计了分布式振动传感器,并通过铅笔断裂模拟裂缝声实验,获得系统的空间分辨率达到5 m,最高频率响应为1 kHz;Z. G.Qin等[3]在相敏光时域反射系统中结合小波变换方法降低系统噪声,将系统的最高探测频率提升到8 kHz;文仲寺等[4]将低通滤波和小波降噪技术结合,提出一种协同滤波降噪方法,将信号的信噪比提升了5.1 dB。
分布式光纤振动传感器作为周界安防、结构健康监测的理想工具,国内外研究的主要方向是突破其性能限制,提升监测事件识别能力[5-6]。由于大多数的外力破坏行为持续时间较短,事件定位与识别对于分布式光纤振动传感系统的实时性有较高的要求,而优化系统数据处理算法是提高系统监测效率的主要途径。这一方面需要优化信号的特征提取和分析算法,提升系统在实际环境中对入侵事件的识别能力[7];另一方面需要提升数据传输及处理速度。黄新锐等[8]提出用于分布式光纤振动传感系统的大数据流压缩传送方法,通过特征提取算法,将数据压缩至原本的0.96‰,提高了系统响应速度。一般使用逐差法对振动事件定位,该算法需要将每次采集的曲线进行作差处理再根据多条差值曲线定位振动事件,但是该方法无法同时获得较好的定位精度和响应时间。本文针对上述问题提出一种基于偏振降噪的比值定位算法,以提高监测系统的实时性、准确性,并且提出一种时域叠加方法强化信号的振动特征,为准确得到振动信号频谱提供保障。
1 POTDR系统原理
POTDR技术是在光时域反射(optical time domain reflectometery,OTDR)技术的基础上改进而来的[9-10],其最早由A.J.Rogers提出并用于测量磁场、电场等物理场的空间分布情况[11]。瑞利散射属于弹性散射[12],当光纤受到应力、振动等外部扰动影响时,双折射效应使得合成的背向瑞利散射光偏振态改变。光纤双折射效应是光纤对2个相互垂直偏振方向上的光具有不同的折射率,当光通过光纤时,使得这2个方向上的光波的传播速度不同,经过一段光纤的传输后,两者的相位差发生改变,进而使得合成光的偏振态发生变化。于是,通过光电探测器检测背向瑞利散射光功率的变化,即可得到传感光纤中各位置点散射光的偏振态信息[13-14],从而分析光纤沿线的振动事件。
然而,通过一条光时域反射曲线只能得到某次测量的各位置点散射光功率信息,无法解调出有效的振动频谱。故需要连续采集多个测量周期的曲线,得到每个位置点对应的时域数据,再对其进行快速傅里叶变换(fast Fourier transform,FFT),从而提取各位置点的振动谱并识别事件。在实际处理中,一方面直接采集到的光时域反射曲线往往信噪比较差,导致事件定位困难;另一方面对所有位置点数据进行FFT,运算量大,降低系统实时性。因此,本文采用先降噪、定位,再进行频谱提取的思路,提高系统的运行速度。
2 信号处理
2.1 信号处理流程
分布式光纤振动传感系统的信号处理流程主要为信号降噪、振动定位、频域变换、特征提取与识别。系统采集的信号含有噪声,噪声主要来源于光电二极管,围绕某固定的电压值波动。降噪的方法有累加平均、低通滤波、小波降噪等。
当前针对振动事件定位的方法有直接频谱法和时域逐差法。直接频谱法对同一位置点在不同时刻的信号进行FFT,若该位置受到振动事件影响,则频谱中将包含该信号特征频率。逐差定位法将相邻周期采集的曲线做差,在振动位置前,偏振态几乎不受影响,差值曲线波动小,而振动位置及其后的位置差值曲线波动剧烈。虽然直接频谱法定位准确,但需要对光纤每个位置的数据进行处理,而振动事件可能仅仅在某个或某几个位置点,增加了系统运算负担。而逐差定位法仅通过差值曲线判断振动位置,由于信号随机波动等原因,使得在不同阈值设定情况下其定位精度不稳定。
此外,由于POTDR系统光时域反射曲线从振动点开始直至光纤尾端都会受到偏振态改变的影响,本系统在定位振动事件后,为提高振动信号振动谱提取能力,提出一种数据时域叠加法,将振动点开始的多个连续位置点对应数据叠加,以强化信号中的振动特征,进而通过FFT得出更准确的振动频谱。
2.2 逐差定位法
逐差定位法是常用的定位方法,将相邻两次测量的光时域反射曲线作差。在受到振动事件影响的位置点之前,曲线差值较小;受到振动事件影响的光纤位置及其后所有位置,差值曲线波动剧烈,然后根据多条差值曲线的波动情况,判断振动事件位置。
在实际应用中,定位前需要先判断振动事件是否存在。假设共有M条背向散射曲线,依次将相邻的2条曲线作差,通过设定阈值的方法判断差值曲线是否存在曲线突增的情况,若存在,则认为存在振动事件并进行定位。对逐差得到的M-1条差值曲线的所有位置点对应数据取绝对值,然后将同一位置点数据相加得到一条叠加平均的曲线。由于原本的每一条差值曲线在受到振动事件影响后,曲线波动由平缓变得剧烈,通过叠加差值的方法强化了振动前后位置点数据的对比,最后通过设定阈值确定振动位置。
传统的逐差定位法在定位振动事件时,需要先对相邻周期曲线作差,若仅使用2条曲线作差,系统灵敏度虽然较高,但是定位误差较大;若多次差值获取多条逐差曲线再判断,需要处理的数据量则会增大,尤其在长距离线路监测中,系统实时性明显变差。
2.3 比值定位法
本文提出了一种新的振动事件定位算法:基于偏振降噪的比值定位法。该算法从步骤上分为振动判断和振动定位,其处理流程如图1所示。

图1 比值定位流程图
采集卡接收的初始数据为一维数据,首先需要根据采集卡的采集长度对一维数据进行整合得到M×N的二维矩阵,表示连续M个脉冲周期采集到的M条光时域反射曲线,每条曲线有N个数据点。然后将M条光时域反射曲线累加平均得到偏振降噪曲线,图2中分别为受振动事件影响前后的偏振降噪曲线,因传感光纤的偏振态的改变会从振动位置处持续到光纤末端,故受振动影响的光纤位置及其后位置的曲线波动平缓。

图2 有无振动时偏振降噪曲线对比
本算法采用去除菲涅尔反射峰后的数据点进行振动事件判断。原则上取的点数越多,判断越准确,但在实际中,振动部分可能靠近光纤尾端,使得受振动影响的光纤长度较短,进而可能影响事件定位及后续振动谱的提取。结合曲线波动规律和实际情况取10个位置点对应数据进行振动判断,求取该10个数据的均值,若其中存在超出范围A的值,则认为曲线波动较大,即无振动事件发生,A的范围设定为均值的0.995倍至1.005倍。通过图3曲线末端对比可以明显看出,受到振动事件影响的曲线末端相较于无振动时更加平缓。

图3 偏振降噪曲线末端对比
在判断存在振动事件后,从既定的末端位置点开始,将前一个位置点的数据与后一个位置的数据相比,得到比值B,若B值在阈值C范围内,则代表曲线波动平缓,继续向前端寻点以此循环得到新的比值B,直至该值超出阈值C的范围,停止循环寻点,将此值对应的2个位置中后一位置定义为振动位置。通过实验对比非振动与振动部分相邻点的比值曲线,如图4所示,发现受到振动事件影响的相邻点比值明显小于无振动部分。对多组实验数据分析表明,将阈值C的范围设定在0.97~1.03较为可靠。

图4 比值曲线
从2种算法的处理流程上看,逐差定位算法首先需要将光时域反射曲线作差,再对差值曲线分别取绝对值后叠加,最后通过设定阈值判断振动位置点。相比之下,比值定位法将所有光时域反射曲线叠加得到一条偏振降噪曲线,再判断是否存在振动事件,最后通过逐点比值判断振动位置点,需要处理的数据量大幅减少,进而优化系统的响应时间。
3 实验及结果分析
3.1 实验搭建
本文设计的分布式光纤振动传感系统的结构如图5所示[15]。脉冲激光器发出光脉冲通过偏振控制器实现起偏,经光纤环形器1端口注入长度约10 km的多模光纤,光脉冲在传播过程中产生的背向散射光经由光纤环形器2端口后,从3端口输出,进入偏振控制器2实现检偏,再由光电探测器将光信号转换成电压信号,最终由数据采集卡采集该电压信号并传入计算机,由计算机进行数据处理分析。本系统中由计算机控制数据采集卡发出触发脉冲同步控制激光器脉冲发射和数据采集。

图5 POTDR系统结构
实验参数设置上,脉冲频率为5 kHz、脉冲宽度为10 ns,脉冲激光器中心波长为1 550 nm,数据采集卡采样率为100 MSPS。实验中需要考虑能否完整采集一个周期的振动信号,故采集时间和累加平均次数需要根据施加的信号特点而定。假设累加平均次数为100次,则FFT后可以探测到的振动事件的最大频率为25 Hz。若加载的振动事件频率为25 Hz,为保证能完整采集一个周期的振动信号,则采集时间至少为4 s,即需要采集200条累加平均100次后的光时域反射曲线。
3.2 实验结果及分析
3.2.1 振动判断测试
实验中,将光纤振动事件加载到光纤末端,由人为拍打光纤模拟振动事件。为了保证采集到包含多个连续周期的振动信号以便于后续通过FFT提取振动谱,实验中采集128条经100次累加平均处理的光时域反射曲线,总的采集时间为2.56 s。使用MATLAB进行数据处理,数据截取不包含菲涅尔反射峰的部分,再将128条光时域反射曲线叠加后求平均,得到偏振降噪曲线。图6(a)、图6(b)分别是施加振动事件前后的偏振降噪曲线,再由本文提出的比值定位算法判断振动事件是否存在,并定位出具体振动位置。图6(a)为无振动事件加载时的曲线,算法准确判断出其无振动事件加载。图6(b)存在振动事件加载,算法定位出振动位置在光纤10 098 m处。

(a)未施加振动

(b)在光纤尾部施加振动图6 振动前后偏振降噪曲线对比
为测试算法的精确度,通过观察全部光时域反射曲线的波动情况得到理论定位点。如图7所示,理论振动定位点位于10 099 m处,与图6(b)中使用比值法得到的10 098 m定位点偏差1 m。
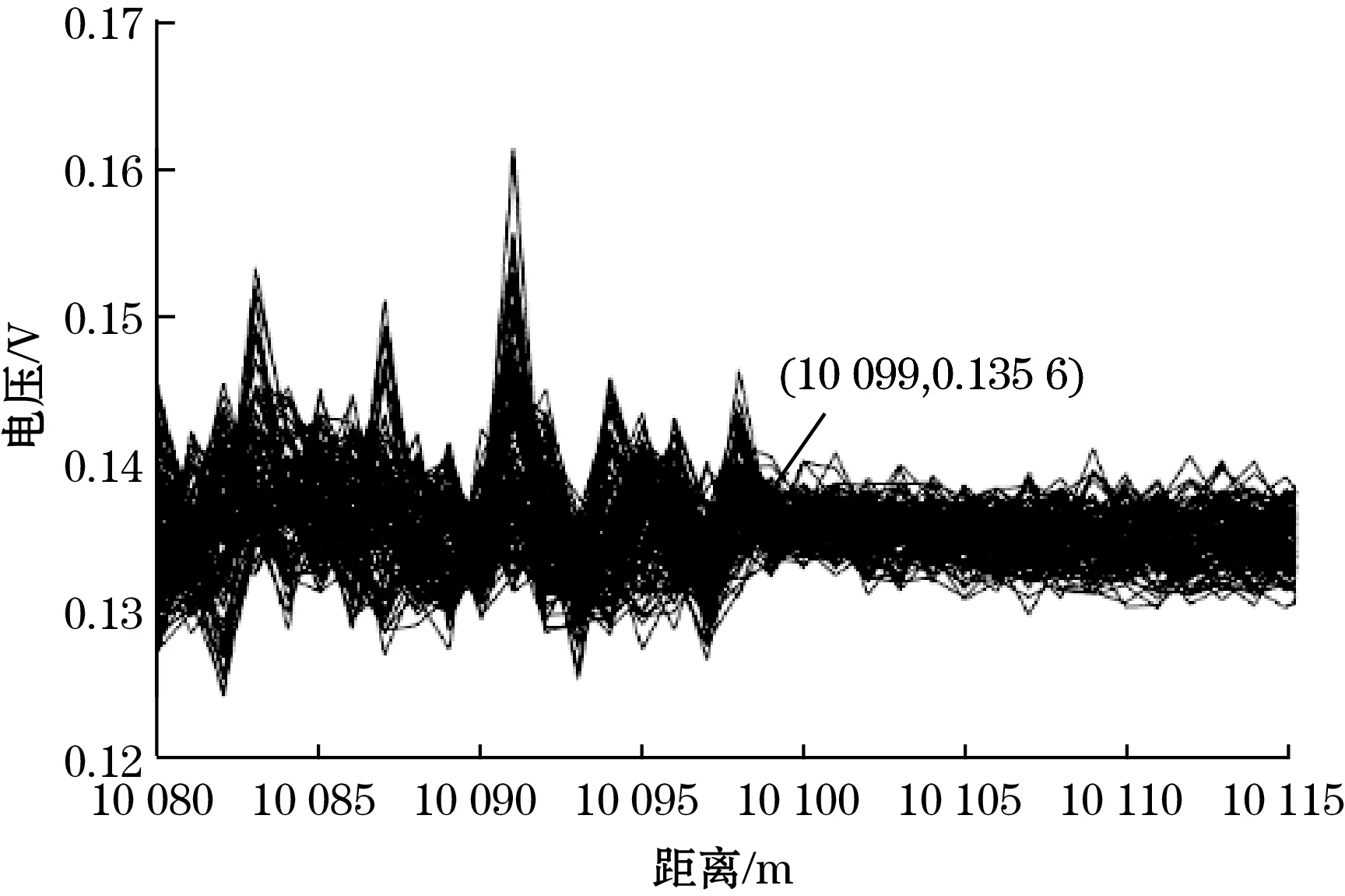
图7 理论振动定位点
3.2.2 算法对比分析
在传感光纤约5 km处加载人为振动事件。采集到128条光时域反射曲线,每条曲线累加平均100次。将128条曲线叠加输出,如图8(a)所示,从图中可以看出本次振动的理论定位点在光纤5 114 m处。

(a)理论定位点

(b)逐差定位法效果
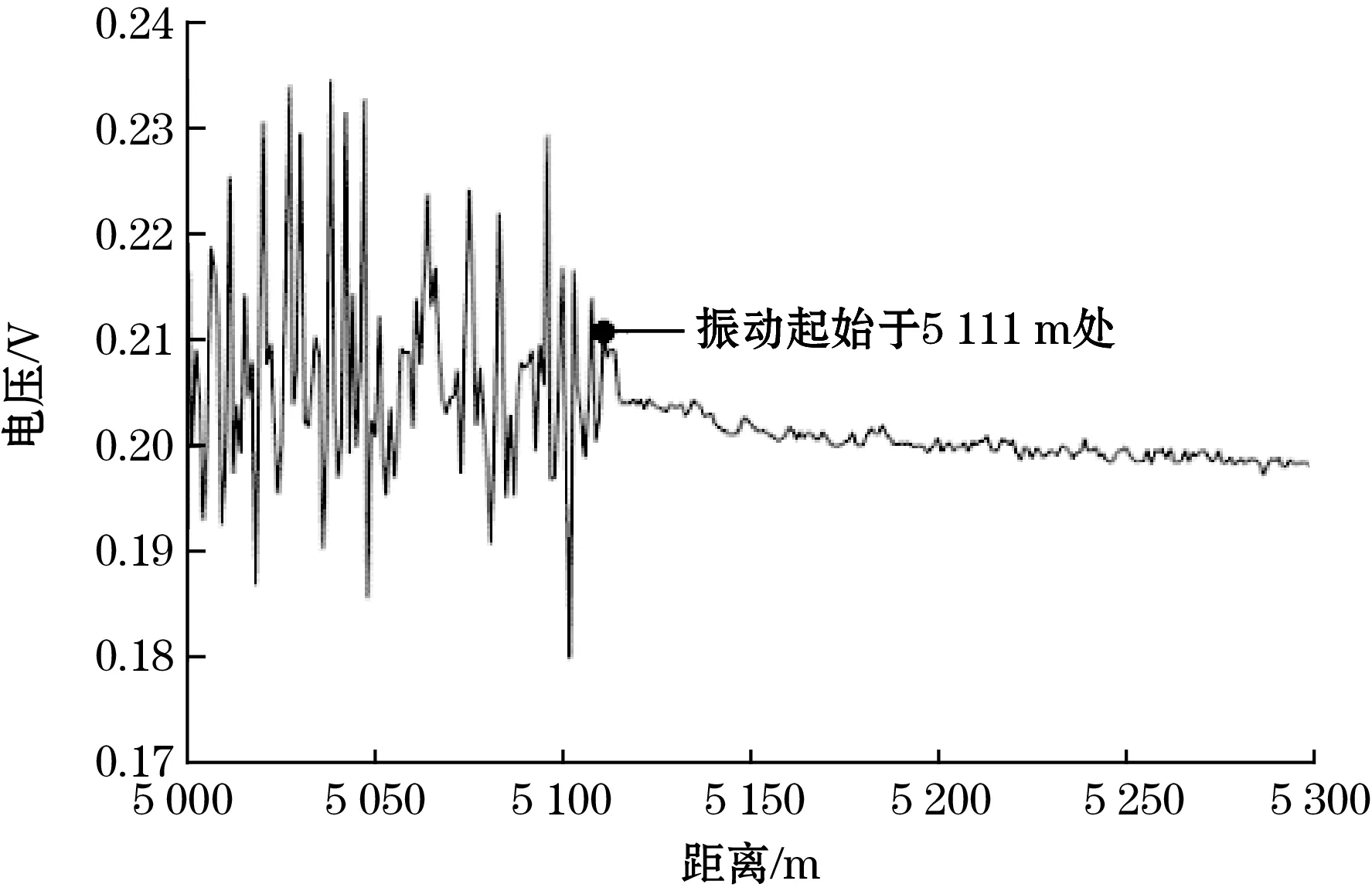
(c)比值定位法效果图8 振动事件定位效果对比
对以上数据分别使用逐差定位法和比值定位法,得到的逐差曲线和偏振降噪曲线分别如图8(b)和8(c)所示,图中已标出各算法处理出的定位点位置。可以看出逐差定位法得到的定位点在光纤5 109 m处,比值定位法得到的定位点在5 111 m处,与直接观察得出的理论定位点5 114 m分别偏差5 m和3 m,显然基于偏振降噪的比值定位算法精度高于传统的逐差定位法。通过对MATLAB运算时间计时,逐差定位法使用了0.37 s完成定位,而比值定位法花费时间0.26 s,运行速度相比逐差定位法提高了30%,可以有效减少POTDR系统数据处理时间,提高系统的实时性。
确定振动位置后,将图8(a)中的每条光时域反射曲线从振动位置点开始的50个连续位置点对应的数据叠加,取均值后得到一个长度为128的数组,再通过FFT得到振动频谱,如图9所示。实验检测到的振动事件频率为6.64 Hz,与实验中对测试光纤施加的振动信号频率一致。

图9 提取到的振动事件频谱
实验表明本文提出的基于偏振降噪的比值定位算法具有较好的可行性及可靠性。本算法可以有效判断光纤沿线是否存在振动事件,若存在振动事件,则系统可以精准定位并得到振动事件频谱。而传统的逐差法由于背向瑞利散射光灵敏性高,相对的误报率较高,若为提高其定位精度而多次逐差,再定位振动位置点,则又增加了数据处理量,降低了对动态事件的监测效率。
4 结论
本文提出了一种适用于POTDR分布式光纤振动传感系统的振动定位算法,该算法通过偏振降噪使振动位置前后的光时域反射曲线出现明显差异,再通过比值定位算法定位出振动事件。该算法利用POTDR系统从振动点开始至传感光纤末端偏振态都会被改变的特性,从曲线的尾端向前端进行寻点,通过相邻位置点数据之间的比值大小来评估光时域反射曲线的突变位置从而实现定位。实验表明比值定位法定位精度高于传统的逐差定位法,最大定位误差为3 m,该算法在MATLAB中的运行处理时间比逐差定位法缩短了约30%。此外,本文提出的信号时域叠加法可强化信号中的振动特征,能有效提取出振动事件频谱。本文设计的分布式光纤振动传感系统及相应振动事件定位与提取算法可应用于管道及其内部设施防外力破坏监测预警。

