基于线结构光的滚动接触表面粗糙度在线测量方法
秦志鹏,吕 庆,闫乐天,杨长辉
(重庆理工大学机械工程学院,重庆 400054)
0 引言
滚动接触疲劳试验是一种模拟轴承、齿轮、轧辊、轮箍等滚动接触零件工况的失效验证试验,是获得机械零部件的设计基础数据的重要手段[1-2]。目前基于二维机器视觉的滚动接触疲劳检测方法[3-4],通过量化试件表面损伤面积评估金属表面宏观疲劳磨损状态,但不能获得试件表面三维微观形貌变化。粗糙度作为表面微观形貌的主要表示形式[5],对机械零件的耐磨性、配合性质稳定性、疲劳强度、抗腐蚀性、密封性和表面光学性能等有着重要的影响[6]。因此,在二维检测基础上,进一步研究滚动接触疲劳试验试件表面三维微观形貌测量方法,在线获取滚动接触疲劳试验过程中的表面粗糙度,对金属材料表面疲劳演变过程研究和疲劳失效预测具有重要的理论意义和实用价值。
根据被测表面是否与测量传感器接触,表面微观形貌测量方法分为接触测量法和非接触测量法[7]。接触测量法中,触针式轮廓仪应用较为成熟,通过探针直接接触被测表面,划过表面的同时记录表面形貌信息,其优点是测量范围较大,精度高[8],缺点是易划伤接触面,测量效率低,只能用于静态表面的离线测量。随着对金属材料的研究不断深入,在线测量需求逐渐增加,基于非接触测量方法是当前研究方向和发展趋势,非接触法的特点是能对被测表面进行无损检测,避免损伤待测表面引起测量误差,同时也能满足在线测量的需要,大幅度提高测量效率,常见的非接触测量法有光切法[9]、干涉法[10]、散斑法[11]、线结构光法等[12]。滚动接触疲劳试验中,被测试件处于转动状态,在表面数据采集过程中需要减小机械振动和轴向跳动的影响,表面粗糙度随着试验进行而不断变化,因此测量方法既要满足测量速度和精度要求,也要具备一定的抗干扰能力。在上述测量方法中,基于线结构光的测量法具有采集数据速度快,测量精度高的特点,也能有效避免轴向跳动对表面轮廓采集影响,满足滚动接触疲劳试验过程中试件表面的粗糙度测量条件。
目前,对线结构光的微观形貌测量研究取得了较大进展,王乐等[13]将线结构光钢轨轮廓测量系统分解为图像采集模块、系统标定模块和轮廓测量模块,在Zemax非序列模式下依次对3个模块进行建模,得到钢轨轮廓测量系统仿真模型,实现对钢轨轮廓测量过程的准确模拟。Z. Shang等[14]提出了一种利用非相干线结构光进行高精度轮廓测量的方法,并研制了相应的测量系统,测得渐开线主齿的齿形误差为±2.2 μm。刘洁等[15]提出一种基于线结构激光传感器的土壤表面粗糙度测量方法,利用半导体红光激光器、CCD 工业相机、计算机及支架等构建测量系统,采集土壤样本的表面图像数据,实现了对土壤颗粒粗糙度的检测。
以上研究验证了线结构光法在表面微观形貌测量的可行性,但针对滚动接触疲劳试验应用较少。基于上述分析,本文提出一种基于线结构光的表面粗糙度测量方法,在滚动接触疲劳试验中采集试件表面形貌信息,在线分析试验中试件表面粗糙度变化,提升滚动接触疲劳试验机微观形貌量化和分析的能力。
1 滚动接触疲劳试验表面粗糙度测量系统
1.1 系统总体设计
系统采用线结构光传感器获取被测表面形貌数据,其原理如图1所示,激光源Op发射一条线激光垂直投射到待测表面形成一条激光亮线AB,AB经过漫反射被受光透镜L接收,并在CMOS上成像。设O点对应成像为Oq,经过坐标转换计算出轮廓AB上P点对应的像点P′坐标,同理可获得轮廓AB上各采集点坐标数据。当被测表面沿X轴向移动时,系统连续记录每次线激光反射回来的形貌信息,若干轮廓线构成试件表面三维点云。

图1 线结构光测量原理
基于上述原理,构建了如图2所示的滚动接触疲劳试验表面粗糙度测量系统。硬件系统中,疲劳试验系统由伺服电机、运动控制卡、试件等组成,试件分为主试件和陪试件,主试件作为被测对象,陪试件在试验过程中与主试件滚动接触,并通过加载系统向主试件施加接触应力;数据采集系统由线结构光轮廓传感器部件组成,试验中系统周期性采集滚子主试件表面点云,并通过软件系统对采集到的点云数据进行在线处理,获得不同循环次数下试件表面粗糙度。

图2 滚动接触疲劳试验表面粗糙度测量系统
1.2 试验平台搭建与点云预处理
由于在滚动接触疲劳试验中,被测试件处于滚动状态,线结构光传感器要有较高的采集速率与精度,本文中选用线结构光传感器型号为基恩士LJ-X8060,在课题组自主研制的滚动接触疲劳试验机CQHH-RCF-A进行试验。根据YB/T 5345—2014《金属材料滚动接触疲劳试验方法》[16],主试件的接触面的加工宽度设定为5 mm。如图3所示,搭建滚动接触疲劳实验表面粗糙度测量实验平台。

(a)滚动接触疲劳试验台

(b)试验样件图3 试件及实验平台
主试件表面点云如图4所示,由x、y、z三坐标离散点构成,其中x轴为轮廓取样方向,轮廓点固定间隔为5 μm;z轴是轮廓高度方向,代表轮廓在传感器视场内的高度值;y轴为线速度方向,间隔Δy计算方法如式(1):

图4 试件表面点云
(1)
式中:fs为传感器采样频率;vy为试件线速度。
试验过程中传感器采集轮廓数据时,由于环境带来的平台振动、光路遮挡和其他外界因素影响,获取的试件表面点云包含一部分噪点,这些噪点的特点是明显偏离原始点云较大距离,称为离群点,会影响后续的粗糙度评定,因此首先要对原始点云中的离群点进行剔除。
本文基于统计滤波方法,统计轮廓点云上每个点与邻域内点的平均距离,根据分布特点来剔除离群点。试件表面点云分布近似服从高斯分布,高斯分布由均值和标准差确定,概率密度函数为
(2)
式中:di为每个点与其邻域内点平均距离;μ为平均距离均值;σ为标准差。
设定每个邻域内点的数量k,利用kd-tree最近邻搜索算法历遍表面点云中的所有轮廓点,其中每个点Pi(i=1,2,…,n)都对应邻域Qi(i=1,2,…,n),计算所有Pi与对应Qi之间的距离di,统计得到均值μ与标准差σ,定义离群点的判定阈值D为
D=μ+∂σ
(3)
式中∂为比例系数。
离群点剔除阈值与选择近邻点的个数k和比例系数∂相关,经验证,当k=30,∂=1.5时,离群点的剔除效果最佳,结果如图5所示。
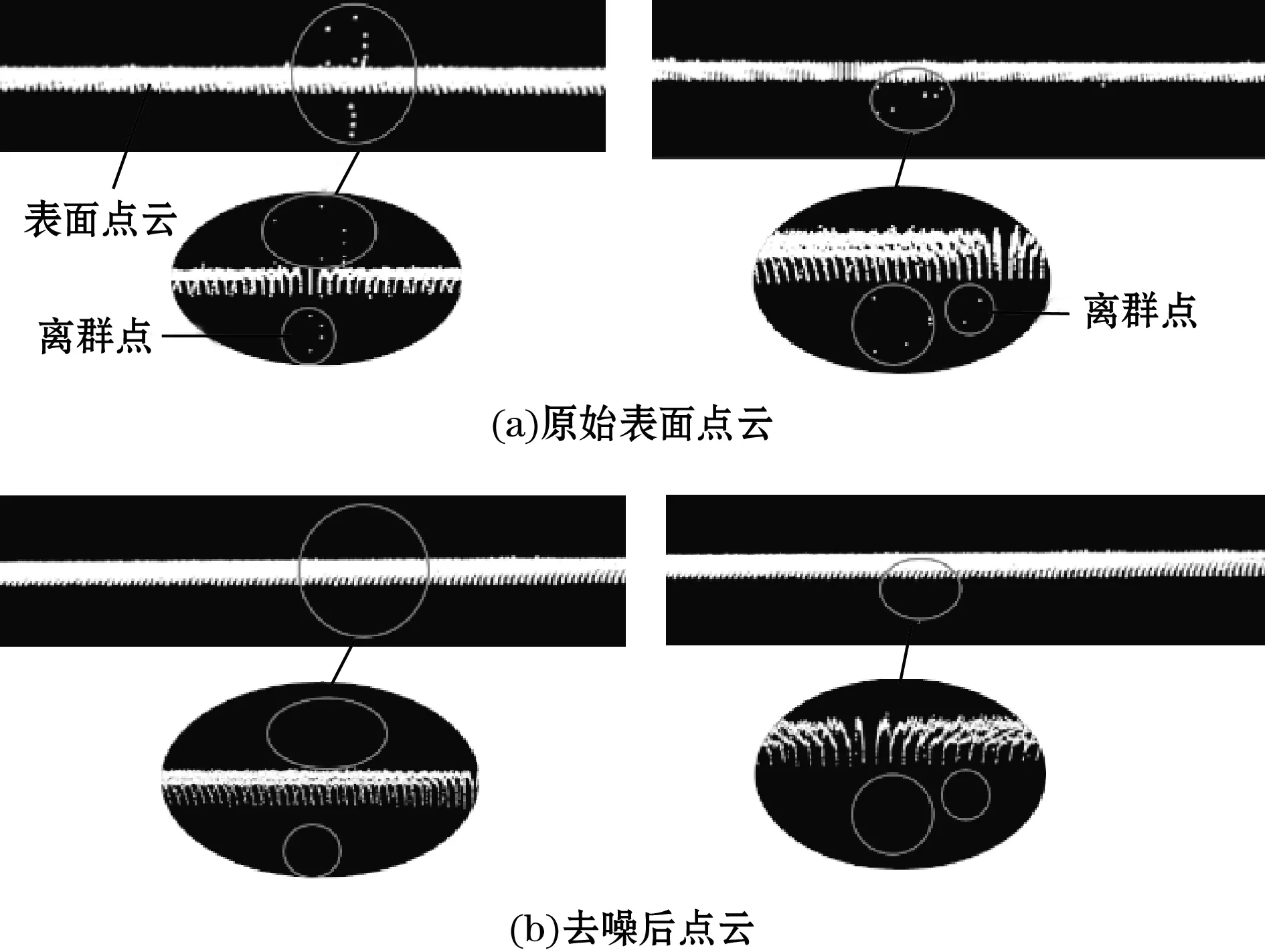
图5 表面点云离群点剔除
2 表面粗糙度计算方法
2.1 表面粗糙度评定标准
根据GB/T 3505—2009《产品几何技术规范(GPS)表面结构 轮廓法术语、定义及表面结构参数》[17]规定,采用轮廓法确定表面结构的术语、定义和参数,关于表面粗糙度的内容主要分为:轮廓构成、取样规则和评定方法。在实际工业场景中,金属零部件材料的表面结构是不规则的,如图6所示,表面轮廓由粗糙度轮廓、波纹度轮廓、形状误差复合而成,三者波距不同。从轮廓波形信号分析,粗糙度轮廓属于高频信号,波纹度轮廓和形状误差属于低频信号,因此可根据频率特征分离出目标轮廓成分。

图6 金属材料表面轮廓构成
用来表述表面粗糙度的数值的符号有Ra(轮廓算术平均偏差)、Ry(轮廓最大高度)和Rz(微观不平度)3种,其中Ra应用最为广泛,本文采用Ra作为评定表面粗糙度的符号。
轮廓的取样方向通常垂直于材料加工方向,选择一定长度的轮廓作为评定表面粗糙度的原始轮廓。为了规范不同表面轮廓特征参数,在GB/T 10610—2009 《产品几何技术规范(GPS) 表面结构 轮廓法 评定表面结构的规则和方法》[18]中规定了轮廓的取样长度和评定长度,在测量表面粗糙度时,取样长度lr的作用是限制轮廓波纹度对粗糙度评定的影响,为保证粗糙度评定结果的可靠性,通常取连续5段取样长度作为粗糙度评定长度ln,计算每个取样长度内粗糙度Rai的平均值作为最终结果,Ra计算公式为
(4)
被测表面粗糙度范围不同,对应的取样长度lr也有所不同,标准中推荐的取样长度和评定长度如表1所示。

表1 Ra取值范围和对应取样长度 mm
2.2 粗糙度轮廓获取方法
由于原始轮廓是由不同成分轮廓复合而成,要提取粗糙度轮廓,首先需要获取具有几何轮廓形状并划分轮廓的基准,即原始轮廓低频成分对应的轮廓中线。通常采用滤波法获取轮廓中线,本文参照GB/T 18777—2009《产品几何技术规范(GPS)表面结构 轮廓法 相位修正滤波器的计量特性》[19],通过高斯滤波器在原始轮廓上加权平均计算,抑制轮廓中的高频成分,获取低频轮廓基准,即高斯滤波中线。高斯滤波器的加权函数定义为
(5)
式中:λ为轮廓波长,mm;λc为高斯滤波器截止波长,mm;a为常数。
傅里叶变换公式为
(6)
高斯滤波器在截止波长处的通过率为50%,即λ=λc,H(λ)=0.5带入式(6)得a=0.467 9。试件表面采集的原始轮廓数据z(x),z(x)由高频粗糙度r(x)和低频波纹度、形状误差w(x)组成。原始轮廓z(x)与高斯滤波器权函数h(λ)一次卷积,得出原始轮廓高斯滤波中线w(x),计算过程为

(7)
将原始轮廓z(x)与高斯滤波中线w(x)作差,进一步得出表面粗糙度轮廓r(x):
r(x)=z(x)-w(x)
(8)
Ra值由粗糙度轮廓r(x)计算获得,定义为在评定长度内,粗糙度轮廓r(x)上每个点纵坐标yi绝对值的平均值:
(9)
2.3 端部效应及修正方法
由于被测表面原始轮廓z(x)取样长度是有限的,而高斯滤波法给定权函数的定义区间[-l1,l2]往往小于原始轮廓的评定长度ln,被测表面轮廓测量长度区间内基于卷积算法的高斯滤波中线w(x)计算如下:

(10)
式中:w(x)为高斯滤波中线;z(x)为待测表面原始轮廓;ln为评定长度。
由式(10)可知,计算的高斯滤波中线w(x)的定义区间为[l2,ln-l1],因此高斯权函数在对原始轮廓加权平均时候仅对轮廓中间部分有效,部分权函数处在轮廓之外,导致高斯函数总权重减少,加权计算后会出现轮廓边界失真的情况,称为端部效应。标准高斯滤波器权函数中l2=l1=λc/2,因此在轮廓左右两端半个截止波长范围内,获取的高斯滤波中线会失真,使得提取的粗糙度轮廓误差较大。因此,需要将高斯滤波中线两端的部分数据舍弃再进行粗糙度计算,而在实际应用中,采集的轮廓数据长度有限,如果直接舍去,得到滤波中线的有效长度太小,评定长度减小会直接影响粗糙度计算值的可靠性。
为了修正端部效应,采用轮廓外延的方法增加原始轮廓左右端长度,使得权函数能够应用到完整轮廓的加权计算。常见外延方法分为3种:补零法、对称延展法和线性外插法。补零法是在原始轮廓两端外λc/2区域填充零,外延区域轮廓高度为0;对称延展法是将轮廓两端λc/2长度区域分别基于点或者直线对称延展,将镜像轮廓作为外延区域;线性外插法是分别将轮廓两端λc/2长度区域线性拟合,根据拟合结果再拓展轮廓。由于加工精度或材料本身的原因,采集到的试件原始轮廓整体是倾斜的,补零法和对称延展法拓展的区间均不符合原始轮廓的倾斜趋势,因此本文采用线性外插法,对轮廓两边端部效应区域进行修正,获取完整的轮廓滤波中线,实现方法如下:

(11)
然后根据拟合结果在原始轮廓上进行线性拓展:
(12)
如图7所示,线性外插法有效修正了传统高斯滤波器端部效应,此方法实现简单,且适用于处理倾斜轮廓的端部效应。

(a)传统高斯滤波器
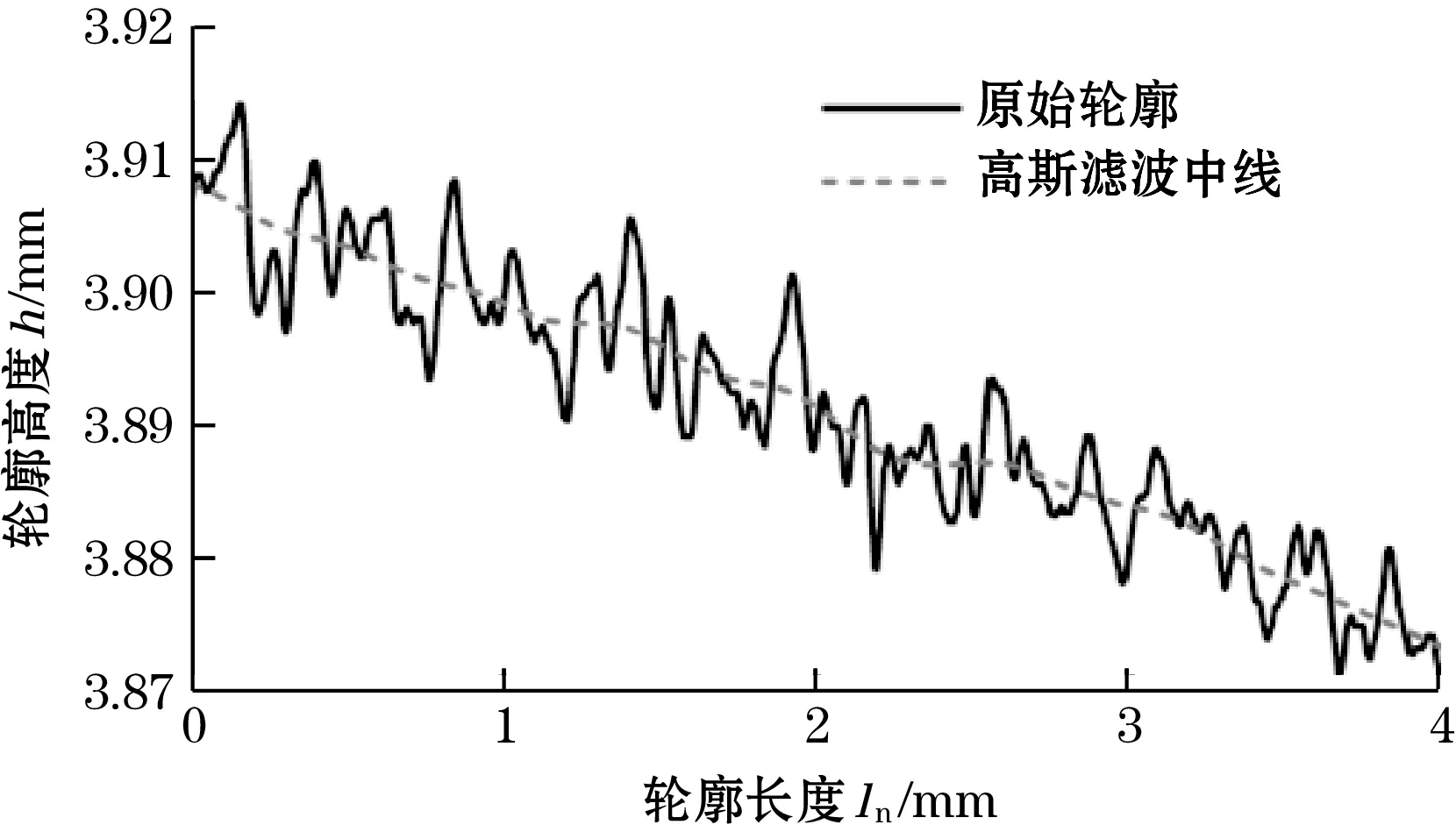
(b)修正后的高斯滤波器图7 高斯滤波中线获取
3 实验结果与分析
试验方案设立2组滚子试件,一组为标准试件,接触面粗糙度Ra分别按照0.8、1.2、1.6 μm加工,测量其表面粗糙度与高精度探针式轮廓仪测量结果对比,验证测量精度。另外一组试件接触面不做处理,在滚动接触疲劳试验中实时记录其表面粗糙度变化并分析。
首先对标准件进行测量,以加工Ra值为0.8 μm的滚子试件为例,测量前先通过探针式轮廓仪测量粗糙度值,经过多次测量得出Ra平均值为0.82 μm。然后通过本文方法采集标准件完整表面点云,进行预处理,点云中包含的若干条轮廓均按以下流程处理:
步骤1:在电机转速10 r/min,传感器采集频率500 Hz时,采集标准件完整表面点云,包含3 000条轮廓。
步骤2:剔除离群点,获取评定表面粗糙度Ra的原始轮廓。
步骤3:采用线性外插法获取修正的高斯滤波中线,结果如图8所示。

图8 高斯滤波中线提取
步骤4:将原始轮廓与高斯滤波中线高度值相减即得出粗糙度轮廓,如图9所示。
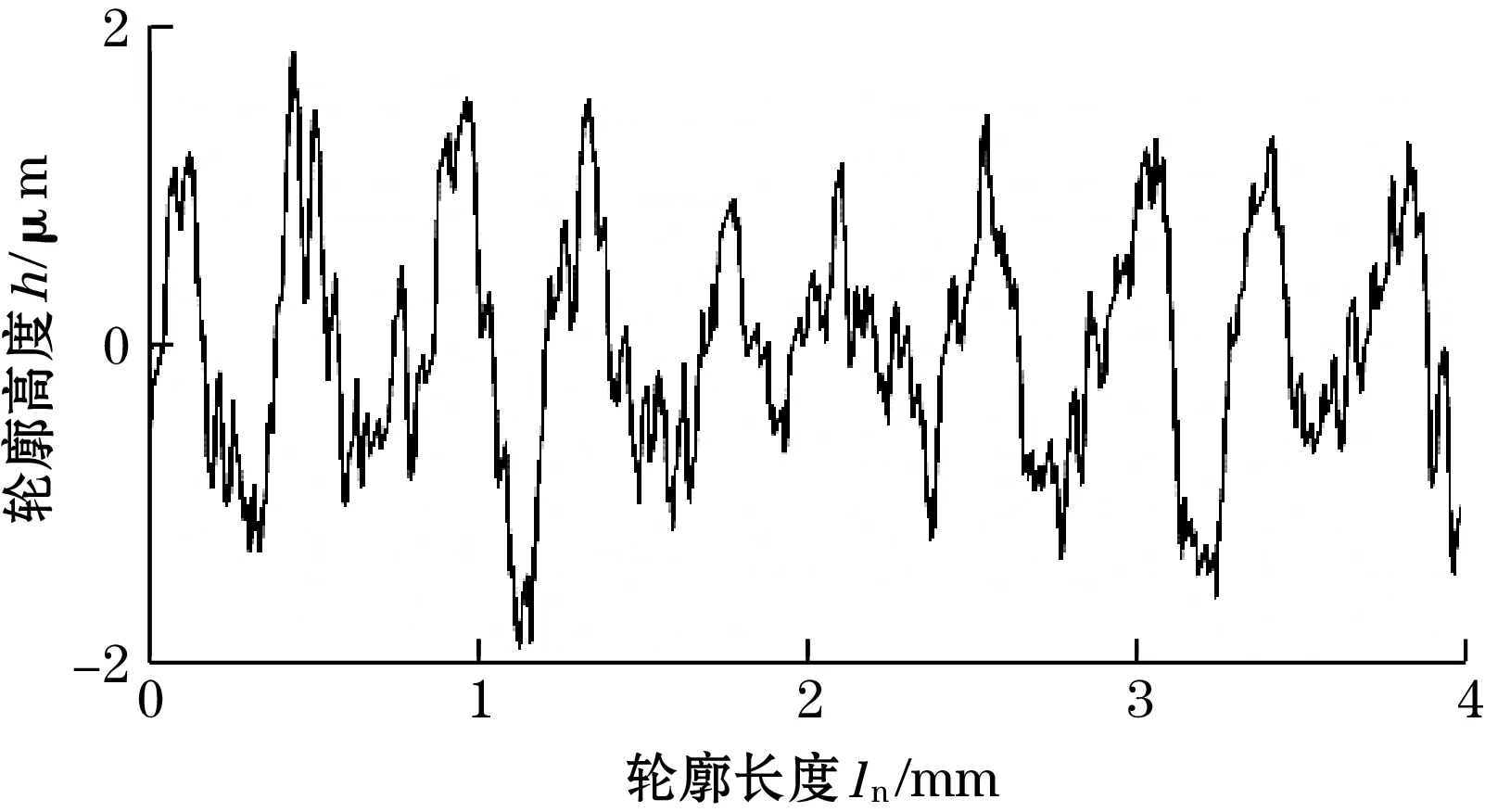
图9 表面粗糙度轮廓
步骤5:根据式(9)求出该标准件的平均Ra值为0.72 μm,采集标准滚子试件表面一周3 000条轮廓,求出Ra平均值为0.78。将其余标准件滚子按照以上流程处理,结果如表2所示。
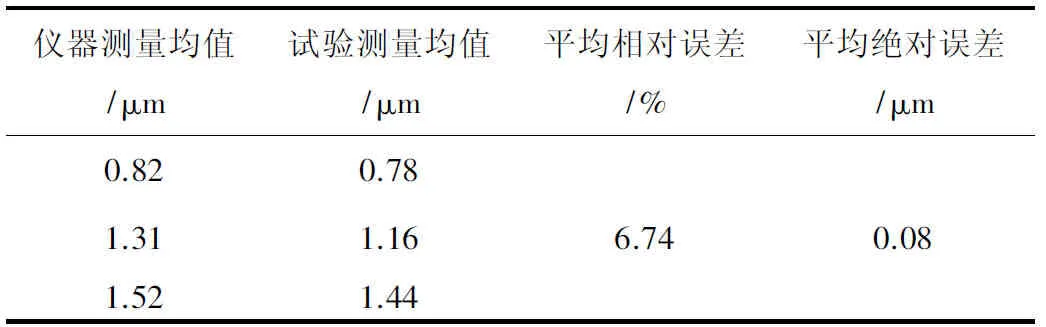
表2 标准件滚子表面粗糙度测量结果对照
通过标准件滚子验证测量精度后,将试验样件安装在滚动接触疲劳试验机上进行滚动接触疲劳试验,按照标准滚动接触疲劳试验工况配置实验环境。
本次试验试件材料主试件、陪试件材料为40Cr,试验载荷2 000 N,主试电机转速500 r/min,主试电机与陪试电机滑差率为10%,每2 000 r采集一次主试件表面点云数据,计算当前表面粗糙度Ra,并绘制粗糙度变化图,结果如图10所示,试验过程中主试件表面点云高度图如图11所示。
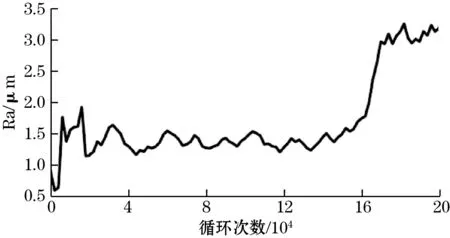
图10 主试件粗糙度变化

(a)主试件初始表面点云

(b)16 000次循环表面点云

(c)40 000次循环表面点云

(d)100 000次循环表面点云

(e)180 000次循环表面点云

(f)200 000次循环表面点云图11 试验过程中试件三维形貌高度图
在滚动接触疲劳试验中,主试件与陪试件两接触面滚动和滑动同时发生,磨损方式为表面疲劳磨损,根据试验结果可以将滚子表面疲劳演变分为3个状态:
(1)跑合阶段:循环次数20 000 r以内,初始摩擦副两接触表面具有较大的形状误差,接触位置峰点压力较大,使得接触力度大,因此在该阶段的磨损程度较深,速度较快,产生较大磨屑,Ra快速增大。摩擦副在磨合过程中接触表面形态逐渐改善,随着接触面积逐渐增加,磨损程度降低,Ra减小,磨损程度相应减小。
(2)稳定磨损阶段:循环次数在20 000~160 000 r内,Ra在1.3 μm左右波动,通过跑合阶段磨损,试件表面加工硬化,凸起变少,粗糙度降低,两试件接触面积增加,试件表面形貌在此期间变化较小,但有一定的塑性形变,磨屑大小均匀呈微粒状。进入稳定磨损阶段。该阶段持续时间越长,材料的稳定性越好。
(3)剧烈磨损阶段:循环次数160 000 r以后,Ra急剧上升,试件表面观察到点蚀剥落现象,出现片状磨屑,从图11(e)可知,在长期循环应力作用下,试件表面塑性形变,进入剧烈磨损阶段。试件已经处于疲劳寿命极限,最终完全疲劳失效,同时表面疲劳演变表现形式由微观粗糙度变化转变为宏观表面剥落面积的改变。
4 结论
本文提出基于线结构光的滚动接触表面粗糙度测量方法能够在线测量金属表面粗糙度信息,弥补了滚动接触疲劳试验的不足。实验结果表明:标准件表面粗糙度测量结果与高精度探针式轮廓仪测量值相对误差小于7%,绝对误差小于0.1 μm,满足滚动接触疲劳试验表面粗糙度测量要求。通过在线记录试件表面粗糙度变化过程,对研究金属摩擦疲劳表面演变过程和失效预测提供了新的试验参考和数据支撑。

