“双循环”下科技金融对企业全要素生产率的影响——基于国家科技金融试点政策的准自然实验

（1.上海对外经贸大学 国际经贸学院，上海 201620；2.厦门大学 经济与管理学院，福建 厦门 361000）

一、引言

2016年7月，国务院将“科技金融”列入《“十三五”国家科技创新规划》，到2017年初，为贯彻实施“双循环”新发展格局，各省份相继出台以科技金融扶持高技术产业的若干政策措施①信息来源于《深圳市龙岗区经济与科技发展专项资金支持金融业发展实施细则》（深龙经促〔2017〕8号）。。科技金融在形成“双循环”新发展格局中能够促进科技与金融结合，缓解企业融资约束，激励企业研发创新，从而提高企业全要素生产率水平。因此，自2010年科技部等五部门发布《促进科技和金融结合试点实施方案》之后，各省份均开始进行一系列实践。截至2010年年底，国家开发银行科技贷款已达到2003亿元；2015—2020年，科技金融进入快速发展阶段。

当前我国处于构建“双循环”新发展格局的关键时期，我国经济发展正逐渐从高速度增长转向高质量发展，提升企业全要素生产率是实现我国经济高质量发展的重要推动力。企业作为微观经济活动的主体，如何通过科技金融的发展提升其全要素生产率，进而促进我国经济高质量发展，亦成为当前学术界研究的重点。有学者采用省级层面数据进行实证研究，发现科技金融发展能够通过优化生产效率显著促进企业全要素生产率的提高（张腾和刘阳，2019）[1]。除此之外，还有学者利用地区相关数据研究发现金融发展可以提高城市全要素生产率，但不同区域的作用效果有所差异（李健和辛冲冲，2020）[2]。但是，金融发展不仅表现为金融规模扩张，还表现为金融结构调整，而金融结构调整能显著促进企业的全要素生产率的提高，因此应同时注重金融规模扩张与结构调整的协调发展（徐清，2016）[3]。还有学者以2008—2016年96家城商行为样本，运用多种估计方法发现地区科技金融发展能显著促进当地企业全要素生产率的提高（董倩，2018）[4]。

在现有文献的基础上，本文的创新点如下。第一，以往的文献主要集中于科技金融发展对各省份的影响，本文则从微观层面探讨科技金融政策对企业全要素生产率水平的影响。第二，由于科技金融政策主要作用对象为科技型企业，因此本文采用2001—2020年高技术行业上市公司数据，确保了样本的精度与广度。第三，本文尝试从融资约束与企业创新能力两个渠道解释科技金融政策对企业全要素生产率的影响机制。第四，本文还探究了科技金融发展对处于不同生命周期、不同产权结构的企业的异质性影响。基于此，本文后续安排如下：第二部分为机制分析与假说提出；第三部分为数据来源与指标测算；第四部分为计量模型设计与实证分析；第五部分为进一步讨论；第六部分为研究结论与政策建议。

二、机制分析与假说提出

本文在相关文献的基础上，构建科技金融与企业全要素生产率的理论模型（Melitz和Ottaviano，2008；李宏亮和谢建国，2018）[5-6]。

在需求层面，沿用M-O的消费者拟线性效用函数形式，考虑采用一个封闭市场模型，消费者在该模型中作为产品的使用者以及生产要素的提供者，企业生产同质或者异质产品。消费者的效用函数为：

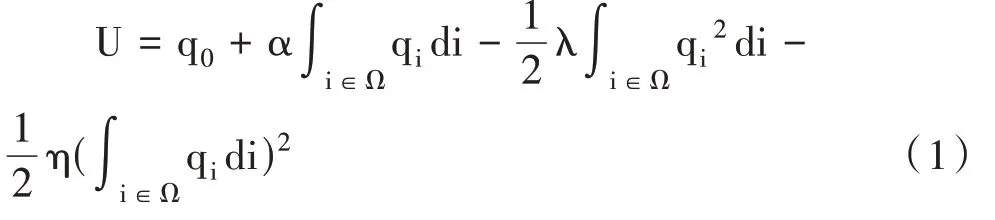
其中，q0和qi分别表示同质产品和差异化产品i的数量，参数α、λ、η均大于0，λ为任意两种差异化产品之间的替代弹性，而α和η则表示同质产品与差异化产品的替代弹性。

消费者在预算约束下可得到产品i的需求函数：

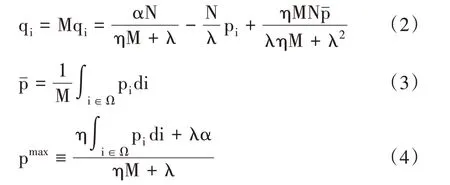
其中，M为差异化产品的种类数；N为消费者数量，代表市场规模；为产品价格指数；pmax是消费量为0时的价格。

在供给层面，根据M-O模型，企业只使用劳动生产要素，即以边际劳动产出来描述企业全要素生产率，当劳动力成本单位化为1时，企业全要素生产率即为边际生产成本的倒数，c(φi)=1/φi，且∂ci/∂φi＜0。当企业处于临界全要素生产率时，利润为0，此时可以得出企业临界边际成本c*=1/φ*。

企业成本函数为：C(qi)=ciqi。由于企业成本ci＜c=pmax，则根据利润最大化条件，可得：

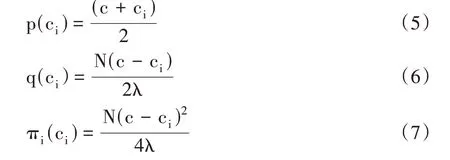
假定企业进入市场后初始全要素生产率水平为1。企业为获取更多的市场份额和垄断利润会根据其初始全要素生产率水平决定其研发创新程度以及所需的外部融资水平。

如果当地的科技金融发展水平为μ，并且企业获得政府与金融市场资金的概率ρi和企业所受融资约束程度ωi，可以推出∂ρi/∂μ＞0，∂ωi/∂μ＜0。企业融资成本是当地科技金融发展水平的函数，当地科技金融水平越高，则该地区的企业就更容易获得外部融资，其所面临的融资约束就越低。假定外部市场单位融资成本为ωi(μ)，并且企业决定投入研发成本γ(Δc)2。企业一般会投入一定比例的内部资金进行研发创新，其比例为κi∈(0，1)，剩余的研发资金1-κi则来自外部市场融资。则企业进行研发创新活动所需成本为：

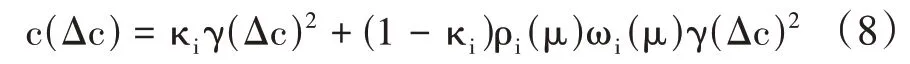
企业为实现利润最大化进行生产，则有：

则企业的全要素生产率可表达为：

令企业全要素生产率对科技金融发展水平求偏导可得出：

式（12）中的一阶偏导大于0表明，科技金融的发展可以促进企业的研发投入并且缓解其融资约束，而企业研发投入的增加以及融资约束的缓解最终会表现为对企业全要素生产率的促进作用，因此，提出待检验的假说1。

借鉴M-O模型，假设企业边际成本服从帕累托分布，即G(c)=(ci/c)k，其中k≥1，0≤ci≤c，由于在位企业边际成本不应大于临界边际成本，因此有c=c*=1/φ*，由于企业全要素生产率越高、边际成本会越低，可以得出企业边际标准差为：

可以看出，科技金融发展会促进企业全要素生产率的提高，降低企业生产的边际成本，只有当企业生产产品的边际成本低于临界边际成本时，企业才会选择生产。因此当临界生产成本越低，该市场下企业的临界生产效率则会越高，企业就会越集中于核心竞争力产品，其全要素生产率离散程度就会越低，集中度会越高。因此提出假说2。

在式（12）的基础上对企业融资约束程度ωi(μ)求偏导，可得：

从式（14）可以看出，随着科技金融发展水平的提高，企业面临的融资约束水平会下降（∂ωi/∂μ减少），当融资约束水平下降时，企业更容易获得金融资金，从而将更多资金用于自身产出的提高，进而提高企业全要素生产率，因此提出假说3。

由于企业研发投入为c(Δc)=κiγ(Δc)2+(1-κi)ρi(μ)ωi(μ)γ(Δc)2，则可得：

令企业研发创新投入对科技金融发展水平求导，可得：

创新是企业提升竞争力的重要渠道，从式（16）可以看出，当地区科技金融发展水平更高时，会吸引更多企业进入，企业为了提升竞争能力，会进行研发创新，而研发创新的成果最终将会用于企业自身全要素生产率水平的提升。这也符合Aiello和Cardamone（2020）[7]的研究结论，即对任何类型企业，进行研发创新投入均能提升企业全要素生产率。基于以上分析，提出假说4。

综上，本文提出如下四个假说。

假说1：科技金融政策能够促进企业全要素生产率的提高。

假说2：科技金融政策促进企业全要素生产率提高，促进其临界边际成本下降，进一步促进企业全要素生产率分布离散程度下降。

假说3：科技金融政策可以通过缓解企业融资约束来提升企业全要素生产率以及企业生产集中度。

假说4：科技金融政策可以通过提升企业创新能力来提升企业全要素生产率和生产集中度。

三、数据来源与指标测算

（一）样本与数据来源

本文数据来自国泰安数据库。样本为2001—2020年全部A股高技术行业上市公司数据，涵盖沪、深两市主板、中小企业板、创业板与科创板，并进行一系列的处理①根据《上市公司行业分类指引》，筛选出化学原料与化学品制造业，化学纤维制造业，医药制造业，通用设备制造业，专用设备制造业，铁路、船舶、航空航天及其他运输材料制造业，电器机械及器材制造业，计算机、通信和其他电子设备制造业，仪器仪表制造业，其他制造业十大制造业，以及互联网及相关服务业，软件和信息技术服务业，研究和试验发展，专业技术服务业四大与高技术制造业配套的服务业；剔除了ST和*ST公司样本；剔除相关财务和公司治理观测数据缺失的样本；剔除2020年新上市的样本；对在1%和99%显著性水平上的主要连续变量逐年进行处理以缓解离群值对结果的潜在影响。根据以上处理方式最终得到14个行业1934家上市公司的11462个观测值，为本文研究的所有数据。。

（二）指标测算

1.全要素生产率

本文被解释变量是企业全要素生产率，本文使用参数法、半参数法和非参数法计算，分别以lntfp_lp、lntfp_op和lntfp_hr表示②OP全要素生产率估计方法的优点是能够同时解决TFP估计时常见的联立性和企业进出造成的样本选择问题，从而得到更有效的估计量。LP全要素生产率的优点是使用中间投入作为全要素生产率的代理变量，中间投入为0的观测值比投资为0的更少，从而能够得到更有效的估计。（Levinsohn和Petrin，2003；Olley和Pakes，1996；Head和Ries，2003）[8-10]。

2.全要素生产率离散程度

本文另一个被解释变量为企业全要素生产率离散程度，借鉴一些学者的研究[11]，采用标准差系数表示，即以标准差除以均值得出，分别以disperson_lp、disperson_op、disperson_hr表示。

3.企业融资约束

本文构建企业运营资本投资敏感性指数（WSK）作为融资约束的代理变量（张杰等，2016；Ding等，2013）[12-13]。

使用两步法估算WSK指数。

第一步，设计企业运营资本投资方程。

其中，WKit是企业运营资本，为流动资产和负债的差值；IWKit为企业运营资本投资，使用当期企业运营资本减去前一期企业运营资本所得；Kt为初始期的固定资产净值。企业层面的控制变量主要包括营业收入增长率、资产负债率、保抵押水平等。此外，还控制了行业固定效应和省份年份固定效应，εit为残差值。

第二步，将企业运营资本投资方程中估计所得的残差值用于第二阶段企业运营资本投资增长率对现金流敏感性指标的计算③这种做法的合理性在于:如果企业运营资本投资不受现金流的影响，那么高现金流的企业的残差均值与低现金流企业的残差均值不会有显著差异；相反，如果企业的运营资本投资与现金流相关，那么经过现金流加权后的随机扰动项均值与未加权的随机扰动项均值就会表现出显著差异。。则i企业在t期融资约束由下式所示：

其中，cashit为i企业t年的现金流，是当年净利润和折旧之和；T为i企业的观测时间长度。

4.企业创新能力

由于上市公司企业研发投入数据自2008年以后开始统计，造成样本部分缺失，因而本文企业创新能力采用企业总的专利数量来衡量，lnpatentit表示i企业在t年专利拥有量对数值。

5.科技金融发展水平

本文核心解释变量为科技金融发展水平，借鉴相关学者的研究，按照“科技资源—经费投入—产出效率”的思路进行设置，分别表示科技金融发展水平相关的资源指数、经费指数、融资指数和产出指数四个方面，采取以下指标综合度量科技金融发展水平（张芷若和谷国锋，2019）[14]。

由于原始数据量纲不同，本文借鉴相关学者的研究，首先对原始数据进行标准化处理，以标准化后的数据通过熵值赋权法得到各指标权重，采用线性加权求和得到科技金融各指标权重的平均值（具体见表1），从而计算得到我国31个省份（不含港、澳、台地区）科技金融发展水平指数（张卫民等，2003）[15]。

图1为2001—2020年我国31个省份的科技金融发展水平分布图。由图1可以看出，科技金融发展水平较高的地区主要分布在北京、上海、广州，其次为江苏、天津、浙江等，即位于京津冀、长三角、珠三角三大经济圈。其中，北京是我国的政治中心，科技金融发展迅速；上海作为国际金融中心，金融资源丰富，2015年金融业已跃居全国首位，成为上海的支柱产业；广东以深圳为代表，为中小科技型企业提供了重要的市场资金来源。此外，作为科技创新产出的载体，北京、上海、广东深圳的科技创新主体对科技金融发展贡献突出。

图2为2001—2020年我国整体科技金融发展水平与高技术企业全要素生产率水平的走势。从图2可以看出，我国科技金融发展水平逐年升高，并在2010年出现小幅度飞跃，自2011年之后呈现不断上升的趋势。此外，上市公司整体全要素生产率水平也呈现出上升趋势，并与科技金融发展水平走势基本趋于一致。图3为2001—2020年我国31个省份的科技金融发展水平与该省份对应的上市公司全要素生产率水平的走势。从图3可以看出，科技金融发展水平较高地区，上市公司全要素生产率水平也较高，并且大多位于北京、广东、上海和江苏等科技金融发展水平较高的省份。

6.主要变量描述性统计

表2列示了主要研究变量的描述性统计结果。

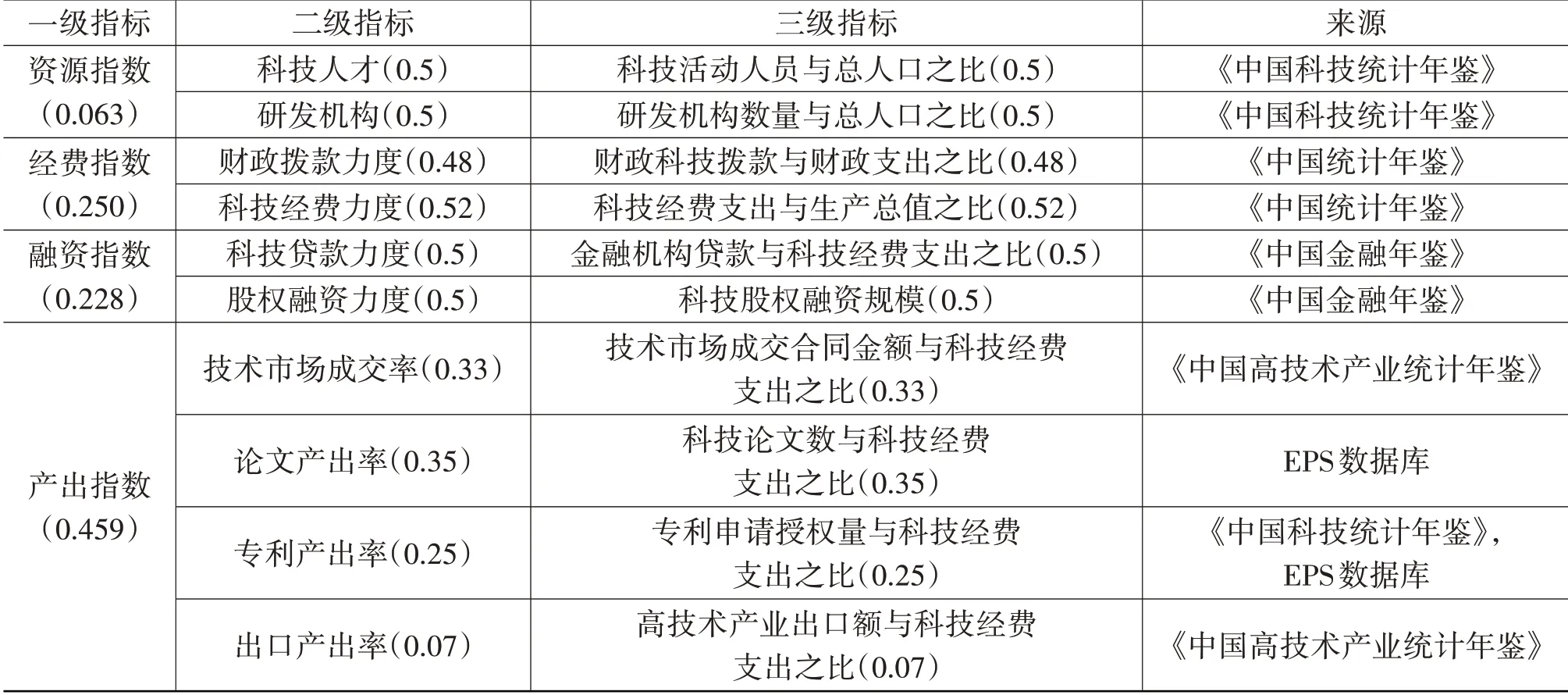
表1 科技金融综合评价体系指标及其权重

图1 2001—2020年我国31个省份科技金融发展水平分布

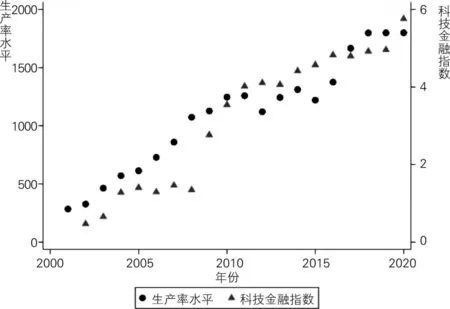
图2 2001—2020年我国整体科技金融发展水平和全要素生产率水平走势

图3 2001—2020年31个省份科技金融发展水平与全要素生产率水平走势

从全样本描述性统计来看，科技金融发展滞后一期指数的平均值分别为0.1702与0.3443，标准差分别为0.1493与0.2127，这表明各省份的科技金融发展指数存在较大差异，并且企业全要素生产率离散程度也较大，这也为本文研究提供了基础。此外还控制了一系列与企业全要素生产率相关的变量①控制变量包括外商直接投资流入程度，金融业生产总值占比，地区外贸依存度，地区产业结构，地区政府干预力度以及企业层面控制变量，如企业规模、企业年龄、企业员工数量、资产负债率、流动比率以及企业成长性。。控制变量的描述性统计因篇幅未具体给出。主要变量的描述性统计结果详见表2。

四、实证模型构建与检验②本文根据实证设计进行分析，结论供参考。

（一）计量模型设计

1.基准回归模型设计

从理论模型中可以看出，地区科技金融的发展将缓解企业融资约束，激励企业进行研发创新，从而促进企业全要素生产率的提高，并进一步降低企业全要素生产率分布的离散程度，提升企业生产集中度。更重要的是，如果该地区的科技金融发展水平较高，更多的企业将会“用脚投票”，将其业务转移到该地区，以便更好地吸收科技金融发展带来的红利。这就带来选择性偏差和互为因果关系等内生性问题。为缓解此内生性问题，本文使用PSM—DID方法来设立基准回归模型。

科技金融试点政策于2011年首次启动，随后于2016年启动第二批试点城市③2011年11月，中国人民银行和中华人民共和国科学技术部首次启动了北京、上海、天津等41个城市作为科技金融试点城市。到2016年，又增加了9个城市。。由于第二批试点涉及的地区较少，而本文研究的时间段为2001—2020年，为了确保结果为2011年的净影响，在接下来的研究中将去掉第二批9个试点城市的样本数据。此外，考虑到2008年金融危机的影响，本文进一步使用2008—2016年的数据进行检验，结果仍然支持这一结论。因此，根据假说1与假说2，DID模型设定如下：

表2 主要变量描述性统计

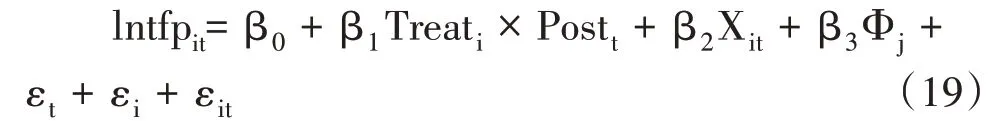
其中，Treati是政策虚拟变量。如果企业位于科技金融试点城市，则值为1；否则，该值为0。Postt是一个时间虚拟变量，2011年政策实施前值为0，2011年后值为1。Treati×Postt为科技金融试点政策的虚拟变量。Фj表示地区层面的控制变量，包括外资流入程度（FDI）以及金融业发展程度（fin_gdp）；Xi表示企业层面的控制变量，包括企业规模（lnsize）、企业年龄（lnage）、员工人数（lnstaff）、资产负债率（lev）、流动比率（debe_ratio）以及企业成长性（growth）；此外还加入固定效应，包括年份固定效应（εt）、个体固定效应（εi），εit为扰动项。最后，确定39个城市为处理组，其他城市为对照组。

由于试点城市的选择不是随机的，会受到区位、资源、发展等因素的影响，因此本文首先采用倾向得分法进行匹配，使用基准回归的控制变量作为匹配的基础，采用近似匹配1∶1的匹配方法，得到适当的样本作为处理组和对照组，并消除不匹配的样本。可以看出，PSM匹配前，对照组与处理组之间存在明显差异，但匹配后，两组之间的差异不明显①PSM的平衡性检验因篇幅原因未详细列出。，因而使用匹配后的样本用于后续的双重差分模型。

2.机制检验模型设计

企业的创新成果和融资能力会影响企业的全要素生产率（张晓莉，2021）[16]。基于假说3，为验证其传递渠道，本文使用中介效应检验方法，设计如下计量模型：

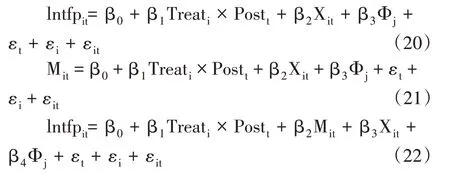
其中，Mit为中介变量，这里主要指融资约束指数WSKit和企业创新能力指标lnpatentit，其余指标同上。

（二）基准回归及平行趋势检验结果

表3显示了PSM匹配后的样本估计结果。交互项对全要素生产率的回归系数显著为正，对全要素生产率离散程度的回归系数显著为负，说明在控制其他因素后，科技金融政策显著促进了企业全要素生产率的提高，显著降低了企业全要素生产率分布的离散程度。表4为进一步的平行趋势检验。结果表明，在政策实施前，处理组与对照组之间差异不大。政策实施后，显著提升了处理组的全要素生产率和生产集中度水平。因此，符合DID的基本假说，再次验证了科技金融政策能够显著提升企业全要素生产率，降低企业全要素生产率分布的离散程度。

（三）稳健性检验

1.内生性检验

为了解决内生性问题，本文借鉴相关学者的研究，采用省级互联网普及率作为工具变量进行两阶段最小二乘估计（谢绚丽等，2018）[17]。使用省级互联网普及率作为工具变量的原因是其与科技金融高度相关，但是与企业全要素生产率弱相关。表5报告了该方法中的LM统计量均在1%的显著性水平上显著，表明该工具变量与科技金融显著相关，又不存在识别不足的问题。此外，由Wald F检验可知，工具变量不存在弱识别的问题。同时，上述检验证明了工具变量的有效性。同时，在加入互联网普及率作为工具变量之后，科技金融政策的交互项系数仍然与基准回归一致，进一步验证了科技金融的发展能显著提高企业全要素生产率水平提升、显著降低全要素生产率分布离散程度，提升生产集中度。

表3 PSM—DID回归结果

表4 平行趋势检验

2.安慰剂检验

对政策虚拟变量进行安慰剂检验，对Treati进行随机抽样，按照初始回归重复进行500次。图4为安慰剂检验的结果，可以看出估计系数分布在0附近，且服从正态分布，符合本文安慰剂检验的预期。

3.其余稳健性检验

（1）由于科技金融政策对企业全要素生产率的作用会受到地区科技金融发展的影响，为了更加稳健地验证本文基准回归得到的结论，在该部分加入前文所计算的地区科技金融指数与政策交互项的三重交互项，分析科技金融政策实施对于科技金融发展情况不同的地区的差异影响。实证结果如表6第（1）列—第（4）列所示，三重交互项的系数显著为正，表明科技金融政策对科技金融发展更好的地区的企业全要素生产率及生产集中度的提升作用更强。

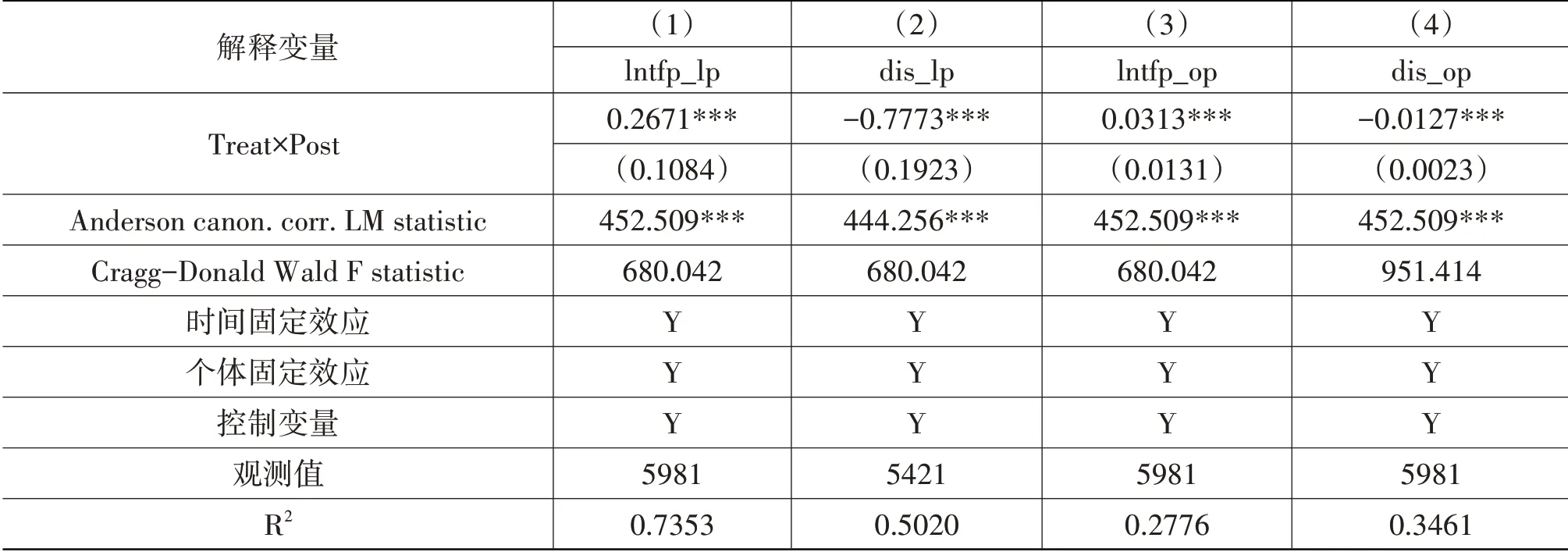
表5 工具变量2sls回归结果

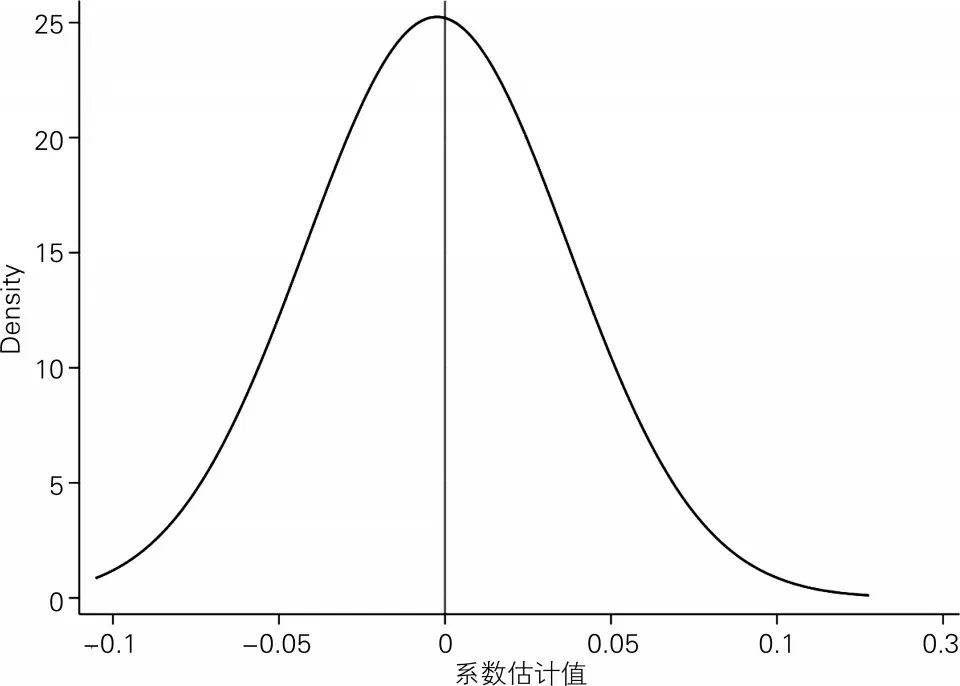
图4 安慰剂检验

（2）使用2008—2016年的样本进行回归分析。由于2008年金融危机之后，我国各省份的金融业或多或少遭受冲击。因此，为了控制2008年金融危机以及2016年第二批试点城市的影响，本文在该部分使用2008—2016年的子样本进行分析。结果如表6第（5）列—第（8）列所示，在使用子样本进行回归并排除了金融危机影响之后，科技金融政策作用效果仍然显著。

（3）加入第二批试点城市进行分析。为了保证样本的全面性，在该部分将第二批试点城市加入回归中。结果如表7第（1）列—第（4）列所示，仍支持本文主要结论。

（4）更换被解释变量。更换企业全要素生产率指标，使用近似全要素生产率的估计方法，方程设为lntfp=ln(y/l)-sln(k/l)。其中，y为企业营业收入；l为从业人员数；k为固定资产规模；s为生产函数中资本的贡献度，设定为1/3。全要素生产率记为lntfp_hr，其标准差系数记为disperson_hr。结果如表7第（5）列—第（6）列所示，科技金融对企业全要素生产率以及生产集中度均有显著的提升作用。

4.机制检验

表8为中介效应回归结果，从第（1）列—第（2）列可以看出，科技金融发展显著促进了企业全要素生产率的提高以及企业全要素生产率集中度的提升；第（3）列—第（4）列表明，科技金融发展显著缓解企业的融资约束以及促进其创新能力的提高；第（5）列—第（8）列在控制了中介变量的基础上，其结果仍然显著。因此可以看出科技金融发展水平的提高会通过提高企业创新能力和缓解融资约束进而提升企业全要素生产率以及其全要素生产率集中度，因而验证了假说3和假说4。

五、进一步讨论

（一）不同生命周期的影响

为了检验科技金融政策对企业全要素生产率及其集中度的提升作用对处于不同生命周期的企业是否存在差异，本文采用留存收益与股东权益的比值（留存收益股权比）作为企业生命周期划分标准。对比留存收益股权比在各取值区间的公司特征，本文将留存收益股权比小于0.1的公司定义为成长期样本，留存收益股权比位于0.1与0.5之间的上市公司定义为成熟期样本，剩余公司为衰退期样本。不同于分样本，本文分别将成长期（LC1）、成熟期（LC2）和衰退期（LC3）企业赋值为1进行交互项回归。回归结果见表9。回归结果显示，科技金融政策对处于成长期企业的全要素生产率和生产集中度产生了显著提升作用；对于成熟期企业来说，其全要素生产率提升作用并不显著；而对于衰退期企业来说，科技金融政策显著促进其全要素生产率的增长，但对生产集中度的提升作用并不显著。这表明科技金融对成长期企业全要素生产率及其生产集中度的提升作用更强，可能是由于成长期企业在其成长过程中由于信息不对称、缺乏成熟的管理、创新能力不足等原因，更容易面临资金短缺、投资不足等困难。因此，科技金融政策会通过缓解融资约束、激励企业研发创新，进而提升成长期企业的全要素生产率。

表6 稳健性检验：考虑地区科技金融发展、使用2008年金融危机后样本

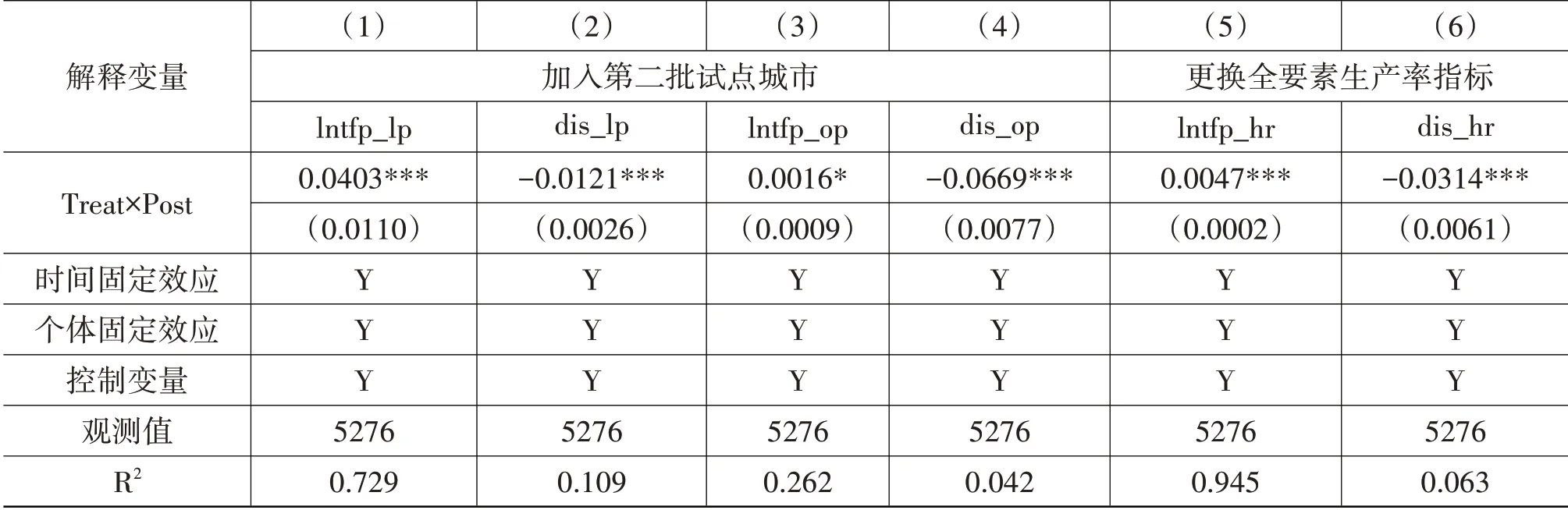
表7 稳健性检验：加入第二批试点城市、更换全要素生产率指标

（二）不同产权性质的影响

为了研究科技金融政策对企业全要素生产率的作用在不同产权性质企业之间的差异，本文按照产权属性将企业分为国有企业（SOE1）、民营企业（SOE2）以及外资企业（SOE3）进行分组回归，依然采用交互项方式。回归结果见表10。回归结果显示，科技金融政策对国有企业的促进作用相对比较明显，可能的原因是：一方面，民营企业相对来说接收和了解相关政策存在一定的时滞；另一方面，本文数据截至2020年，未捕捉到近期的政策效应和政策后期作用的影响。

表8 中介效应检验结果

六、本文结论与政策建议

（一）主要结论

在“双循环”新发展格局下，提高企业全要素生产率对促进国家经济发展具有一定的意义，而地区科技金融政策为企业提供了丰富的资本与技术资源，对企业全要素生产率的提升起着重要作用。本文采用2001—2020年A股高新技术产业上市公司数据，探究科技金融政策对不同类型的企业全要素生产率的影响。主要结论如下：（1）通过图像分析可以看出，近年来我国各省份科技金融发展虽整体呈现增长趋势，但表现出明显的不平衡性，科技金融发展水平较高的地区主要在京津冀、长三角、珠三角三大经济圈；（2）基准回归发现，科技金融政策能够显著促进企业全要素生产率及生产集中度的提升；（3）机制检验表明，科技金融政策主要通过缓解企业融资约束以及提高企业研发能力，促进企业全要素生产率及生产集中度的提升；（4）异质性检验表明，科技金融的发展对于不同生命周期、不同产权性质的企业会产生差异性影响，科技金融政策能显著促进成长期和国有企业全要素生产率和生产集中度的提升。

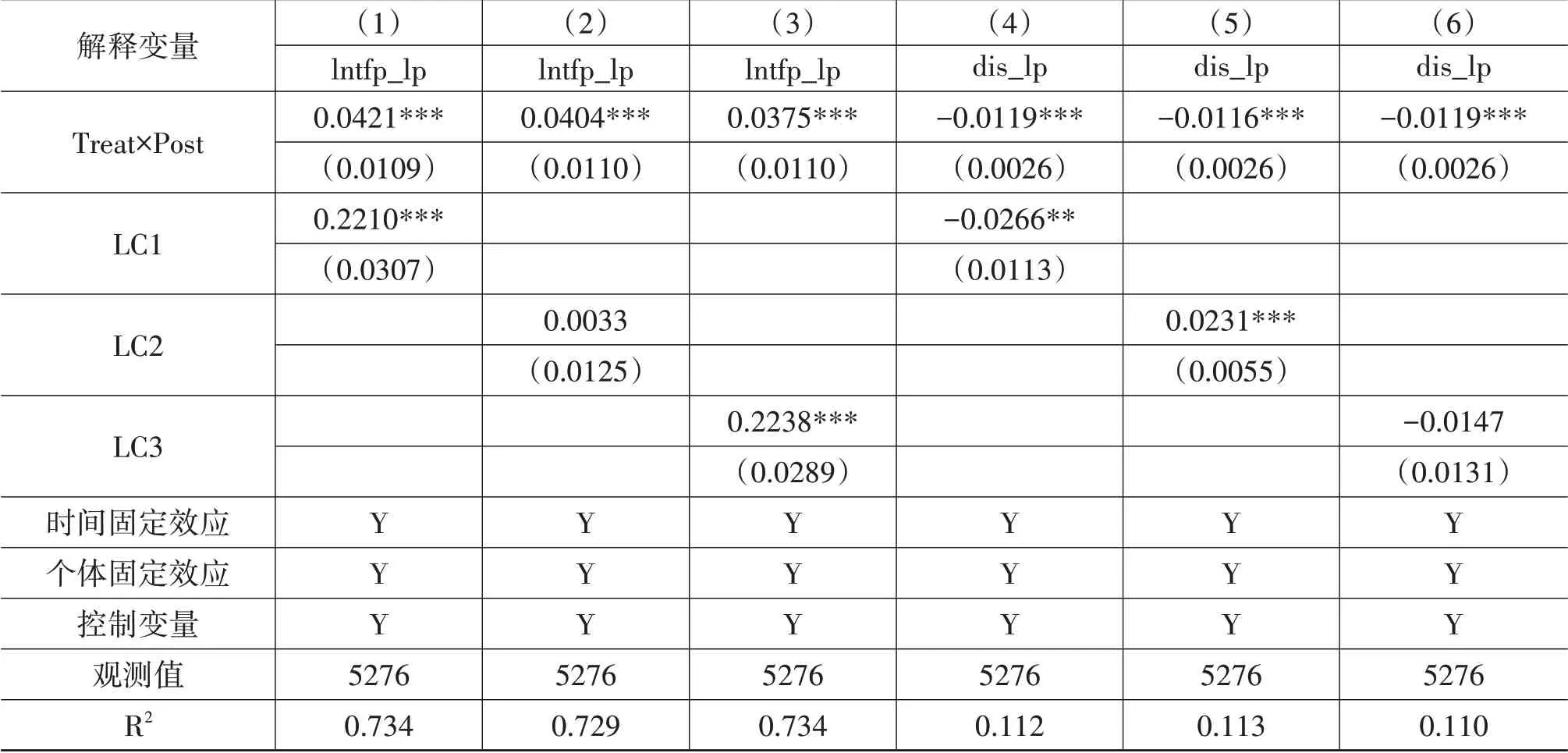
表9 基于不同生命周期企业的异质性检验结果

表10 基于不同产权性质企业的异质性检验结果

（二）政策建议

基于上述研究结论和当前科技金融发展的实际情况，本文提出如下建议。

第一，考虑地区科技金融发展不平衡性。在进一步完善科技金融政策之前，应充分考虑到各地区科技金融发展水平，准确评估科技财政预算、配套金融体系以及当地企业发展状况，根据实际情况制定合理政策。

第二，将缓解融资约束、降低融资成本作为发力点。加强对科技金融政策专项基金的管理并放大商业金融的杠杆效应，在管理专项资金时，既要提高资金的利用效率，又要注重资金施予的公平性。积极促进当前效益不佳的科技型中小企业的成果转化，为其发展提供机会和路径。

第三，深化科技金融改革，助力实体经济。持续引导科技金融政策的实施，并考虑将其作为提升中小企业和民营企业全要素生产率和生产集中度的重要手段之一。防止由于科技金融发展的不平衡性对地区经济和地区中小企业产生不利的影响。

第四，企业应强化自身创新能力和金融风险管理的能力，积极寻求政策支持。中小企业和私营企业应积极寻求发展策略，及时了解政策信息与动态，主动寻求科技金融政策支持。抓住科技金融发展的机遇，积极投入研发创新，实现自身的蓬勃发展。