基于GWO优化ICEEMDAN分解的混合储能系统功率分配策略*

刘 勇 刘大鹏 穆 勇 李振成 王 顺

(国网冀北电力有限公司唐山供电公司 唐山 063000)

1 引言

风电等可再生能源的发展可有效缓解全球能源短缺问题[1-3]，但由于风电出力的波动性和间歇性，风电直接并网会影响电力系统的安全稳定运行。配电网中配置混和储能系统可以改善风电出力，减小风电波动，但混合储能系统应用的关键在于良好的控制策略[4]。因此，用于风电平抑的混合储能系统功率分配策略仍是一个亟待解决的问题。

国内外对混合储能系统功率分配策略的研究已获得较多的研究成果。文献[5-7]采用小波包分解风电功率，利用频谱分析确定混合储能系统功率划分分界点，最后利用模糊控制器保证储能介质工作在健康状态。但采用小波包处理信号时，存在小波基和分解层数难以确定从而导致风电并网功率提取不全面的问题，文献[8]采用基于经验模态分解(Empirical mode decomposition，EMD)风电功率，根据储能系统荷电状态(State of charge，SOC)自适应调整蓄电池和超级电容器的功率，实现储能系统功率的分配。为解决 EMD分解本身存在边界效应和模态混叠问题，文献[9]采用集合经验模态分解(Ensemble empirical mode decomposition，EEMD)处理风电原始信号，并提出混合储能系统能量管理协调控制算法，实现储能系统内部能量流动。由于EEMD在处理信号时，引入的白噪声导致信号在重构分解产生误差，文献[10]提出一种指数滤波法提取风电并网功率后结合自适应噪声的完整集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)，分解混合储能系统功率，通过SOC调整储能功率分界点，实现储能内部协同工作。文献[11-13]提出一种利用自适应的VMD结合模糊控制实现储能功率分配的方法，该方法可以有效解决频谱混叠问题，但在采用VMD时，分解模态数和二次惩罚因子对信号重构具有较大影响，上述两个变量难以选择。文献[14]采用二阶低通滤波算法处理风电信号，以SOC作为检测指标，实现储能介质功率的分段优化调整。但二阶滤波算法的时延及时间常数选取困难等问题，均会导致混合储能系统配置不合理。ICEEMDAN在处理信号时不存在小波基选取问题，较 EMD、EEMD、CEEMDAN、VMD等信号处理方法，具有伪模态数少、不存在模态混叠现象等优点，因此本文选择采用ICEEMDAN处理风电信号，获得风电并网功率。

采用混合储能系统平抑风电波动的关键在于合理的储能系统控制策略，而储能系统控制策略的优劣与风电并网功率的获取和储能功率的分配方法密切相关。因此，本文将从风电并网功率的获取和储能功率的分配方法两方面入手。针对上述文献提取风电并网功率不全面的问题，本文采用ICEEMDAN处理风电信号，但存在参数信噪比μ难以正确选择的问题，因此采用 GWO寻优信噪比μ，同时确定高频、低频功率分量分界点k，实现风电并网功率的获取。针对目前文献多采用实际经验下超级电容的充放电响应时间作为混合储能功率划分标准，缺乏理论依据，难以合适地进行混合储能功率划分，本文以各相邻高频IMF分量信息熵作为指标，实现储能系统功率的一次分配。最后，考虑储能荷电状态约束，采用模糊控制优化修正储能介质的功率，保证储能介质正常工作，避免过充、过放行为的发生。

2 基于 GWO-ICEEMDAN风电功率分解

为更全面地获取风电并网功率，以减小风电对储能系统的容量配置需求，本文采用 GWOICEEMDAN分解风电功率，获取风电并网功率。首先，初始化信噪比μ参数，生成灰狼种群，对风电功率Pw进行ICEEMDAN分解。统计分解产生的各IMF分量个数l，以风电并网功率P0波动量ΔP为指标，循环迭代k值，当ΔP满足表1所示现行国家标准规定的ΔP的最大限值，令k=k-1，继续迭代，直至 ΔP不满足国家风电并网有功波动要求，停止迭代k值，计算此过程所有狼群适应度值。其次，更新灰狼算法参数a、A、C，继续上述步骤，直至达到灰狼算法最大迭代次数。最终，确定ICEEMDAN参数信噪比μ值，以及高频、低频功率分量分界点k，最终确定风电并网功率P0以及混合储能系统功率Pgp。GWO-ICEEMDAN分解风电功率控制策略流程如图1所示。

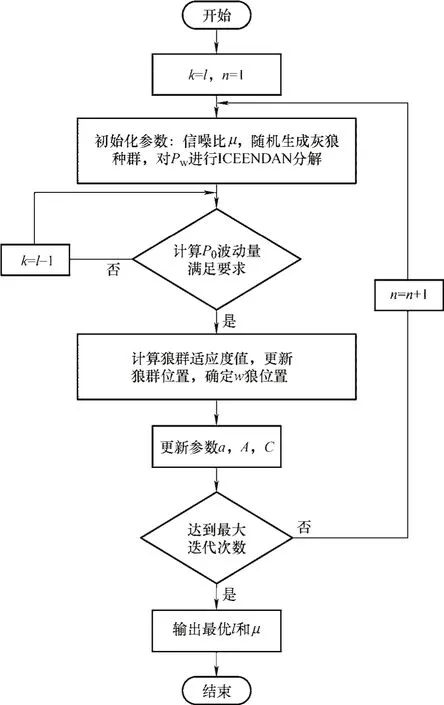
图1 GWO-ICEEMDAN分解风电功率控制策略流程图

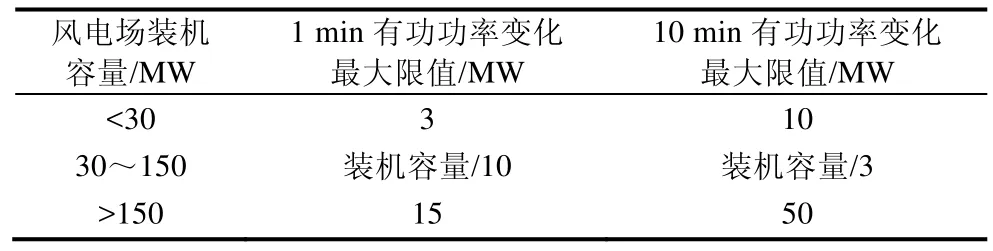
表1 风电场有功功率变化的最大限值

风电并网功率P0和混合储能系统功率Pgp计算如式(1)所示

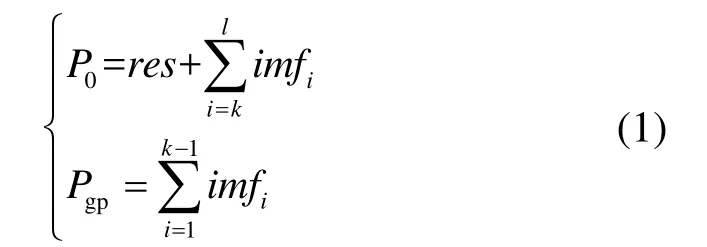
式中，i=1,2,3,…,l；l为 IMF分量个数；res为ICEEMDAN分解风电信号产生的残量信号。

P0波动量ΔP计算如式(2)所示

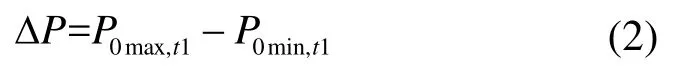
式中，P0max,t1和P0min,t1分别表示以10 min为时间尺度下低频功率分量的最大值和最小值；t1表示以10 min为时间尺度段数，t1=1, 2, …,T/600，T为采样总时长。

2.1 改进的自适应噪声的完备集成经验模态分解

CEEMDAN在处理风电信号时，产生的各IMF分量含有少量噪声，且产生伪模态分量，不利于风电并网功率的获取。ICEEMDAN在CEEMDAN算法的基础上进行优化改进，通过将模态估计转化为局部均值估计，真实IMF分量由残差与局部均值的平均值之差求得，改进的CEEMDAN可以更好地解决上述问题[15]。ICEEMDAN算法如下所示。

(1) 首先，对原始信号Pw进行加L次噪声处理，产生L个新信号PwL(t)，如式(3)所示

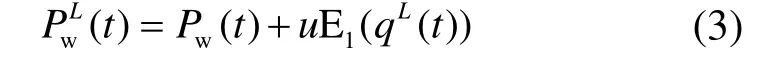
式中，E1表示进行一次 EMD分解；qL(t)表示第L次加入的白噪声。

(2) 对L个信号PwL(t)进行EMD处理，得到1阶残差res1和1阶模态函数imf1如式(4)所示

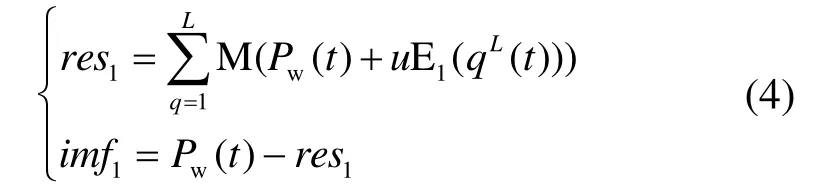
式中，M(·)表示求取平均值。

(3) 将每次产生的残差信号作为新信号重复步骤 1、2，计算第l阶残差resl和l阶模态函数imfl如式(5)所示

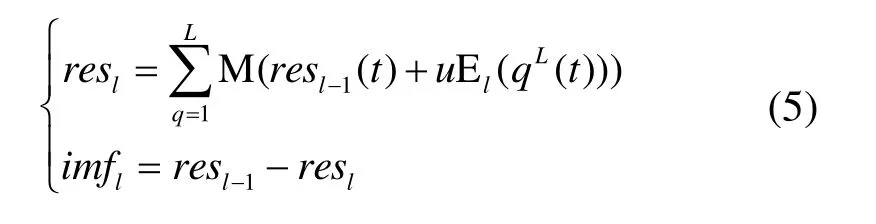
式中，resl-1表示第l-1阶残差。

(4) 重复上述步骤，直至残差无法被分解，此时原始信号Pw表示如式(6)所示。ICEEMDAN算法原理图如图2所示。

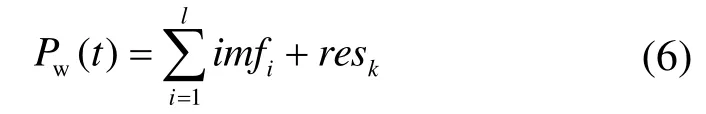
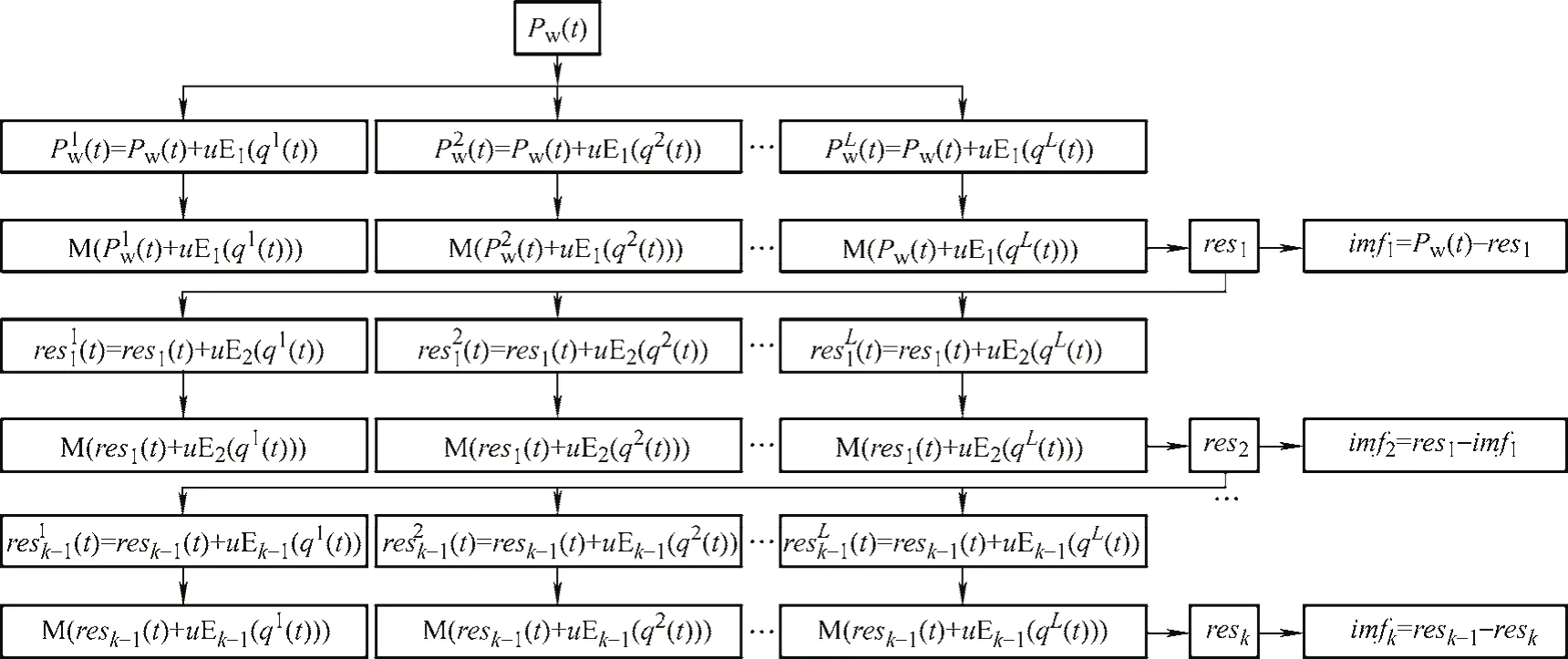
图2 ICEEMDAN算法原理图

2.2 灰狼优化算法

灰狼算法是模拟自然界狼群搜寻捕捉猎物而提出的一种元启发式算法。该算法编写简单，收敛速度快，不易陷入局部最优，且在函数优化问题中优于粒子群等其他智能优化算法[16]。GWO算法定义每次寻优结束后，适应度排名前三的灰狼为α、β、δ狼，其余狼定义为w狼，w狼服从α、β、δ狼。狼群追踪猎物的数学模型定义如式(7)、(8)所示。

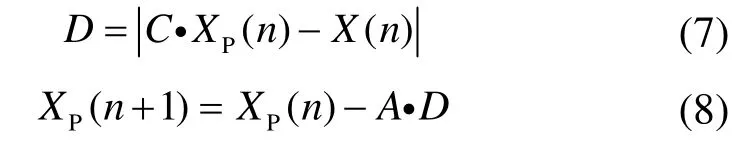
式中，D表示灰狼个体与猎物之间距离；A、C表示系数向量，计算方法如式(9)、(10)所示；n表示迭代次数；Xp、X分别表示猎物和狼位置。

式中，a表示收敛因子，由2线性减小到0；r1、r2为[0, 1]之间的随机数。

在追踪狩猎过程中，如图3所示狼群不断更新其位置，该模式的数学模型如式(11)～(13)所示[17]。

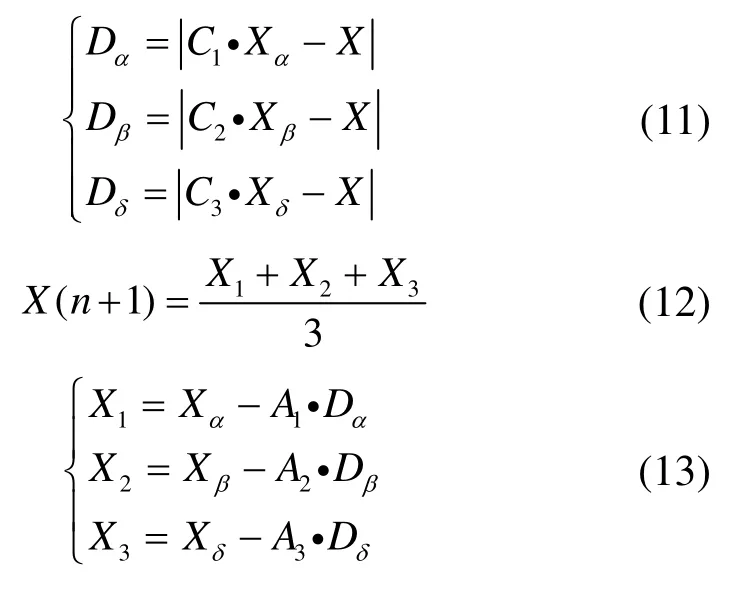
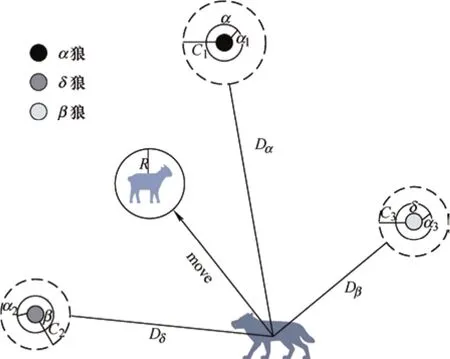
图3 GWO算法中灰狼位置更新示意图

GWO算法中适应度函数的构建对狼群进化狩猎等模式具有较大影响，结合ICEEMDAN算法，综合考虑P0与Pw的互相关系数、以及经ICEEMDAN分解获得的各 IMF样本熵，采用CRITIC权重法[17]，构建GWO的适应度函数f如式(14)所示。样本熵用于反映各IMF分量的频率特征是否明显，当熵值越大，则表示ICEEMDAN参数选取越不合理，模态混叠现象严重；P0与Pw的互相关系数反映了风电并网功率和原始风电信号的波形相似程度，互相关系数值越大，表明风电利用率越高，此时对储能的配置需求越小，更加经济。

式中，sampEn为样本熵函数；q表示维度；r表示相似容限；B表示在相似容限r下匹配q,q+1个实数的概率；a为风电并网功率；b为原始信号；ai、bi分别为信号a、b第i个数据点的值；分别为信号a、b的平均值；N为待测信号数据点总数。

3 基于信息熵-模糊控制的混合储能功率控制

统计计算各imfi之间的信息熵，找出特高频分量Ptg和次高频分量Pcg的分界点W，进而对第2节所获得的混合储能系统功率Pgp进行划分，将Ptg分配给超级电容器，将Pcg分配给蓄电池，实现储能介质功率的一次分配。上述储能功率一次分配过程未考虑储能SOC约束，超级电容器可能存在过充过放行为，减小储能系统的寿命，进而影响风电平抑效果。通过采用模糊控制，修正蓄电池、超级电容器的功率，实现储能介质功率的二次分配，最终通过如图4所示的风储系统实现风电平抑。

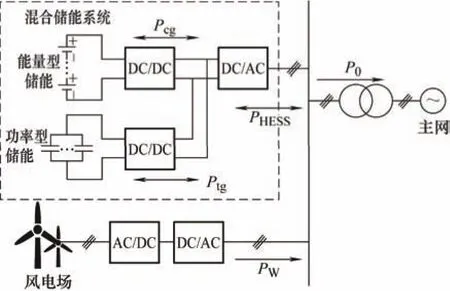
图4 风-储联合系统拓扑图

3.1 基于信息熵的混合储能功率一次分配

信息熵主要用于衡量变量之间的依存性，通过式(17)计算各imfi之间的信息熵R(imfi,imfi+1)，R(imfi,imfi+1)越大，表示两IMF信号彼此的依存性越大，所包含的信息越多[18]。

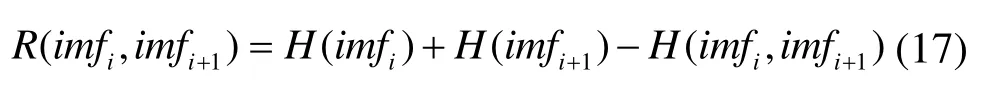
式中，H(·)对信号熵值计算。

由于经 ICEEMDAN分解的Pw，其产生的各IMF信号是由高频到低频排列的，结合信息论相关内容可知：当两个信号完全不相关，则信息熵为0[19]。可知在进行Pw分解重构各IMF信号时，R(imfi,imfi+1)必存在一个由小变大的过程，因此以第一个极小值点作为特高频分量Ptg和次高频分量Pcg的分界点W。根据分界点W重构出Ptg、Pcg功率如式(18)所示

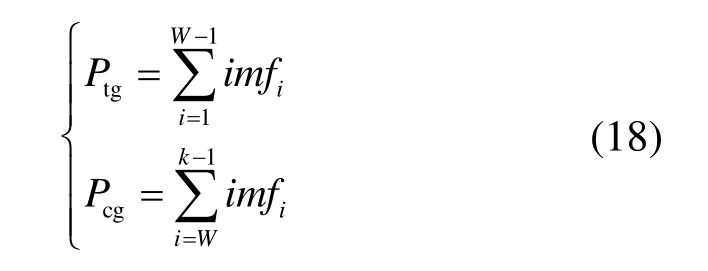
3.2 基于模糊控制的混合储能功率二次分配

第3.1节所述储能功率一次分配过程未考虑储能SOC约束，超级电容器可能存在过充过放行为，减小储能系统的寿命，难以保证储能系统工作于最佳状态，针对上述问题，采用模糊控制对功率型以及能量型储能功率进行修正。

当超级电容器 SOCtg在合适状态时，不需要对混合储能功率进行修正。当 SOCtg过大或过小，而此时储能下一状态处于充电或放电时，采用模糊理论对其SOCtg进行控制，以当前 SOCtg和下一时刻所需SOCtg的变化值ΔSOCtg作为模糊输入，ΔSOCtg计算如式(19)所示，模糊输出为Ptg的修正系数M。模糊输入SOCtg的论域为[0, 1]，模糊集为{VS，S，MS，M，B，VB}。模糊输入 ΔSOCtg的论域均为[-1,1]，模糊集为{NB，NM，NS，PS，PM，PB}。模糊控制器输出量M的论域为[0, 1]，模糊集合为{VS，S，MS，MB，B，VB}。SOCtg、ΔSOCtg、M隶属函数及模糊规则、模糊控制器输入输出关系[8]分别如图5、6和表2所示。

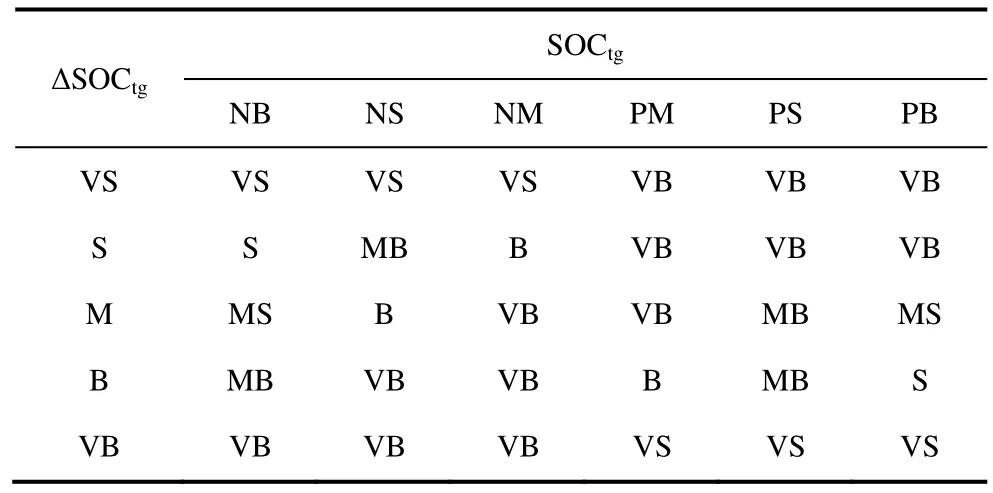
表2 模糊控制规则

图5中，VS、S、MS、M、MB、B、VB、NB、NM、NS、PS、PM、PB分别代表非常小、小、中小、中、中大、大、非常大、负大、负中、负小、正小、正中、正大。

图5 模糊控制输入、输出的隶属函数

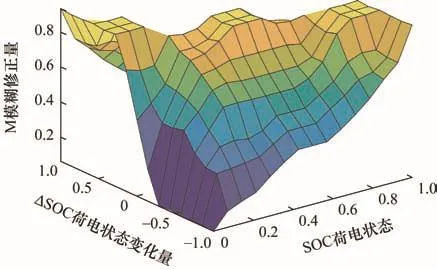
图6 模糊控制器输入输出关系

式中，tc1、tc2、td1、td2分别为储能充、放电起止时刻；ηcg、ηdg分别为超级电容充、放电效率；Etgr为超级电容的额定容量。蓄电池额定容量的计算过程与超级电容的计算过程相同。

储能的额定容量Etgr由储能的能量变化情况和SOC约束条件求得。

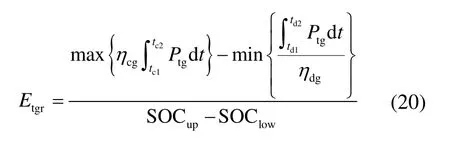
式中，SOCup、SOClow分别为超级电容的荷电状态上下限。

修正后功率型和能量型储能功率按式(21)计算。

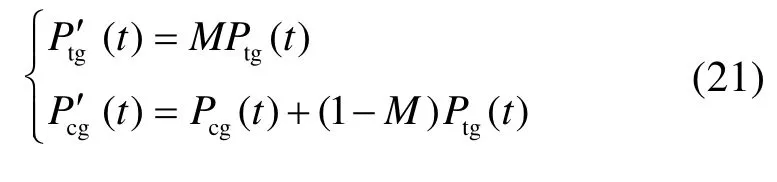
4 仿真分析

本文采用装机容量为60 MW的风电站某典型日实际输出功率数据，采样时间为5 min，灰狼种群规模为30只，最大迭代次数为20，利用Matlab对原始风电数据进行处理，表3储能系统相关参数取自文献[20]。

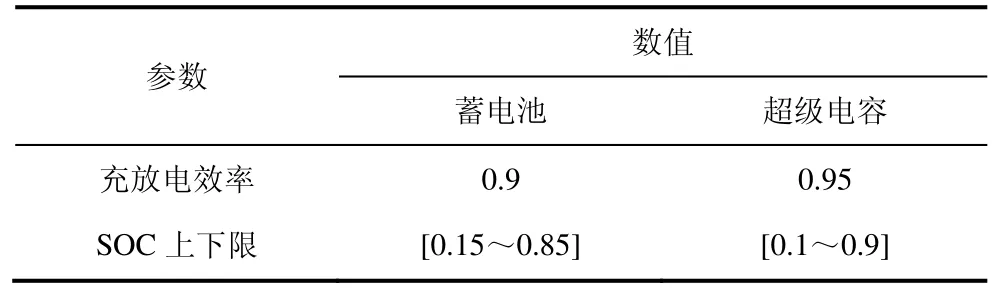
表3 储能系统参数

4.1 风电并网功率获取效果分析

为解决ICEEMDAN分解风电功率时，信噪比参数μ难以正确选择的问题，采用GWO进行参数寻优，结果如图7所示。

图7 GWO优化ICEEMDAN参数结果

根据图7所示GWO优化ICEEMDAN参数结果可知，GWO算法在第14次迭代时，找到最优μ和k分别为 0.3和 4。将信噪比参数 0.3代入ICEEMDAN算法中进行风电功率分解，以k=4作为高低频分量分界点，获取风电并网功率P0以及混合储能系统功率Pgp如图8所示。

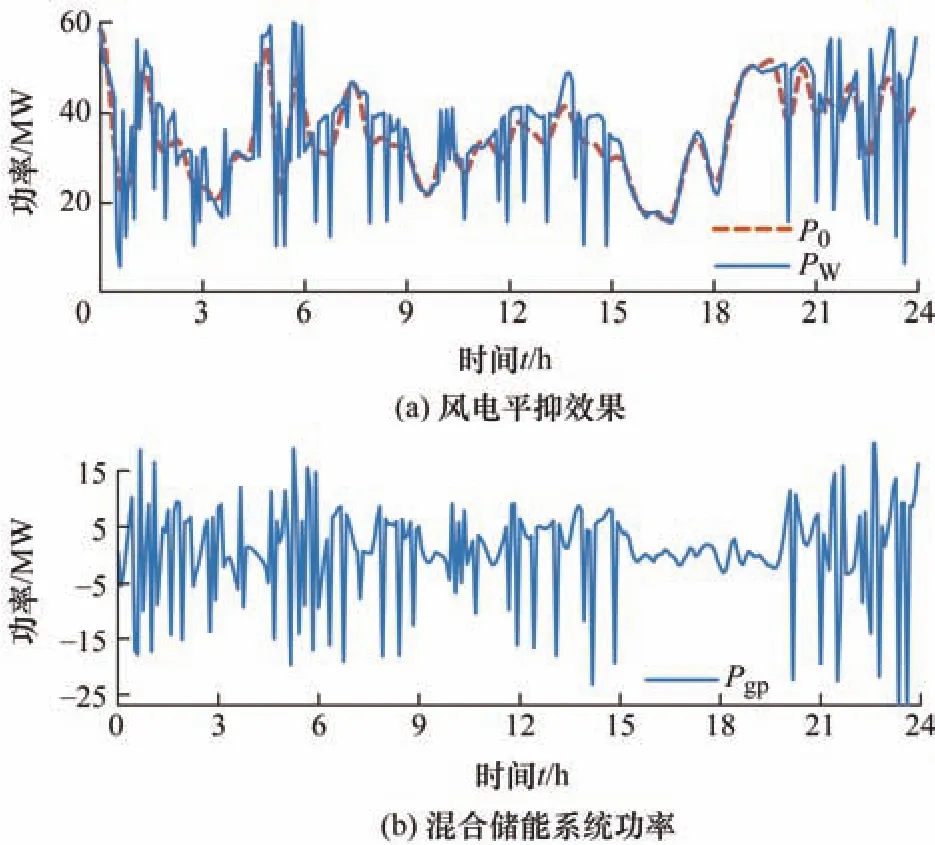
图8 风电并网功率以及混合储能系统功率

根据式(2)计算 ΔP，绘制如图9所示的风电并网功率波动率曲线，由图9可知，经过风电平抑后获得的功率，波动性大大减小，装机容量为60 MW的风电场最大有功波动为18 MW，满足表1所示的风电场有功功率变化的最大限值，验证了本文设计的采用GWO-ICEEMDAN获取风电并网功率的有效性。

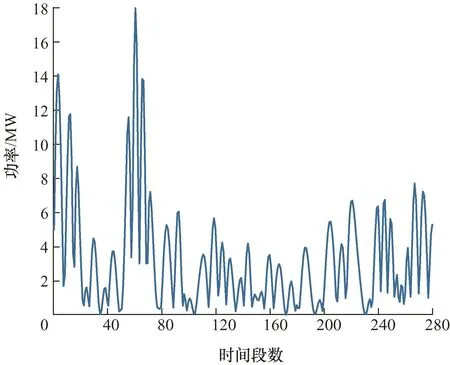
图9 风电并网功率波动ΔP

为证明GWO算法的优势，分别采用粒子群算法和GWO算法优化处理ICEEMDAN参数，其结果如图10所示。由图10可知GWO算法在第14次迭代时适应度最小为 0.66，而粒子群算法在第 17次迭代时适应度最小为0.674，仿真结果表明GWO算法计算速度以及计算精度均优于粒子群算法。

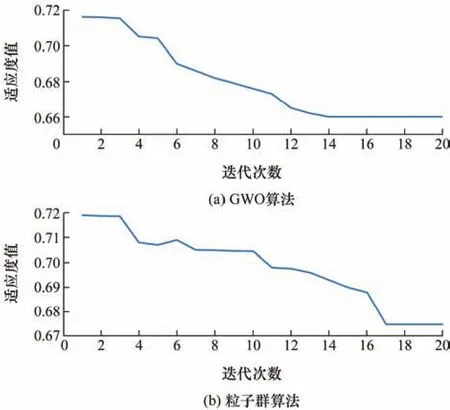
图10 GWO算法和粒子群算法的迭代计算结果

为证明ICEEMDAN在处理风电信号时的优越性，本文选取常见的4种提取风电并网功率的方法(表4)，与本文方法进行对比分析。

表4 用于对比分析的4种风电平抑方法

首先采用方法1、2、3、4将Pw分解，获得各IMF分量如图11所示。

根据图11中4种方法对Pw的分解结果可知，采用 GWO-ICEEMDAN的信号处理方法，较CEEMDAN分解方法，可以减少信号分解产生的伪模态数目，进而减少所需分析的信号数目，有利于缩短混合储能功率分配时间。目前在采用ICEEMDAN处理信号时参数信噪比μ的选取皆按人为经验选取，μ的经验选取标准如下：信噪比μ越大，对原始风功率信号的影响越小，最终分解的IMF经过重构后越接近原始信号；信噪比μ越小，将削弱噪声对原始信号高频部分产生的互补作用。综上考虑重构以及互补作用的影响，目前文献对信噪比μ多取值为 0.1。采用灰狼算法优化的ICEEMDAN和未加入采用灰狼算法优化μ取0.1时的ICEEMDAN风电分解效果对比结果分别如图11c和图11d所示。对比分析图11c和图11d可知，未引入GWO优化参数的ICEEMDAN分解难以正确选择信噪比μ，导致伪模态数增多，增加了信号处理数目，不利于快速进行混合系统功率分配。

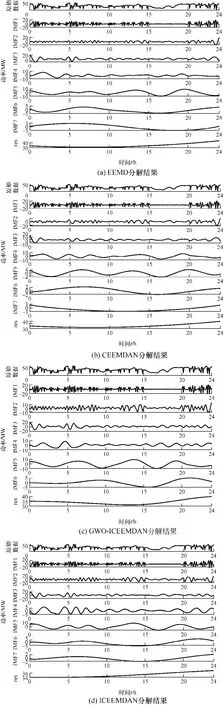
图11 4种方法对Pw的分解结果

从信号迭代处理次数比较GWO-ICEEMDAN和EEMD，利用两方法处理Pw，生成的各IMF分量所含噪声随信号叠加处理次数关系如图12所示，结果表明当采用 EEMD处理信号迭代次数过少时，在各IMF分量中存在大量白噪声，进而影响混合储能系统功率的获取。虽然增加信号处理次数达到600时，可以忽略白噪声的含量，但相应会增加信号处理时间。

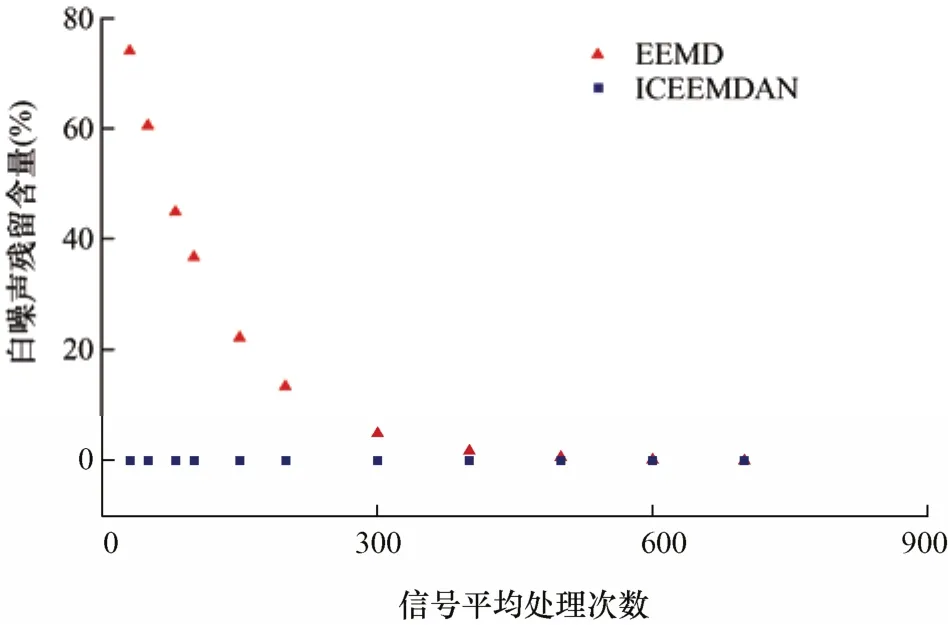
图12 各IMF包含噪声含量结果

本文采用的处理器型号为 Inter(R) Pentium(R)Gold G5400 CPU @3.70 GHz 3.70 GHz计算机，对上述三种方法进行仿真分析，各方法的风电平抑效果如图13所示，GWO-ICEEMDAN、EEMD、CEEMDAN分解获取风电并网功率耗时分别为6.81 s、8.42 s、7.34 s，证明了采用 GWO-ICEEMDAN方法可以快速实时获取风电并网功率且对计算机性能要求不高。

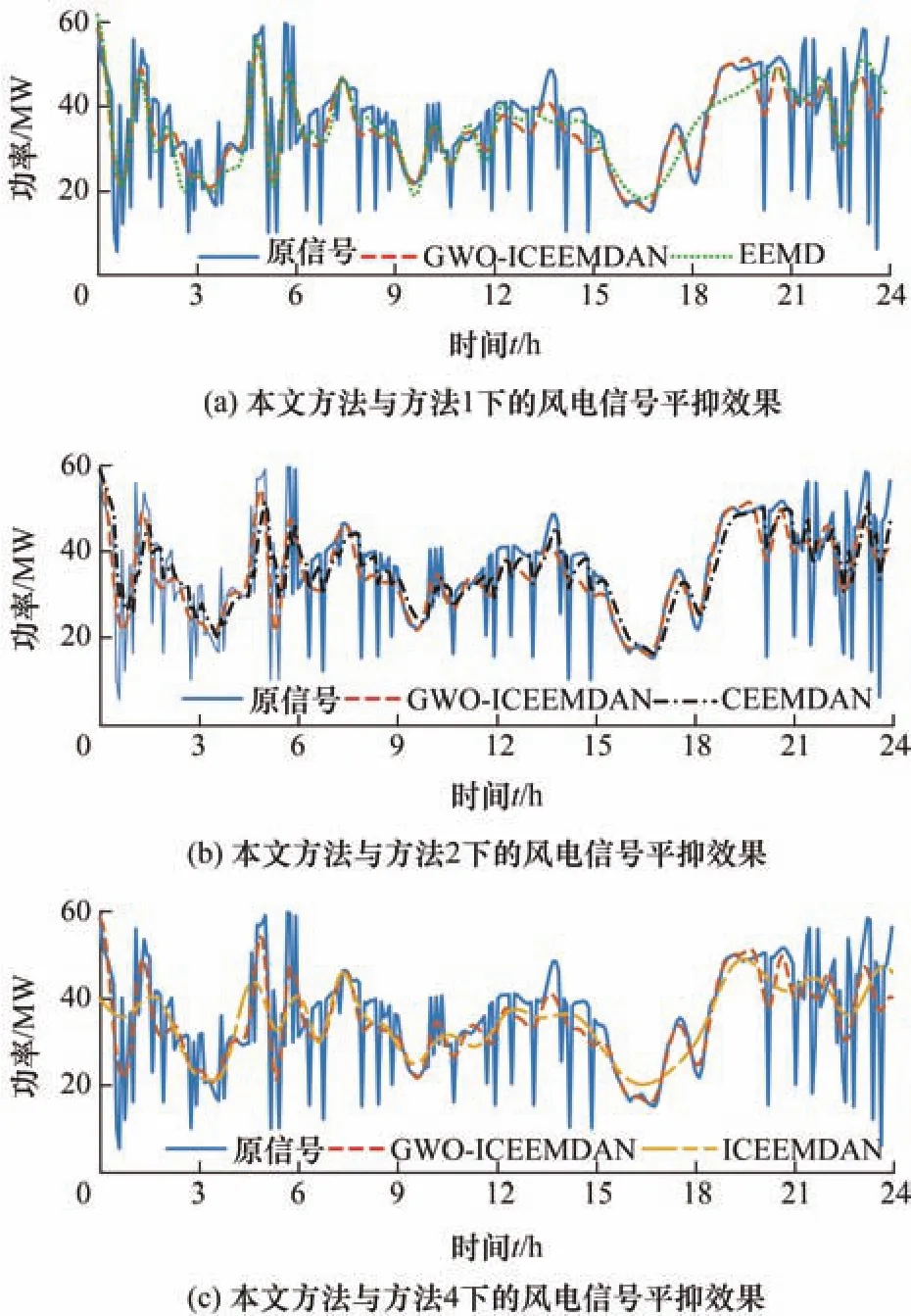
图13 三种方法下的风电信号平抑效果

如图13所示，从风电信号平抑效果角度对比分析上述4种方法，本文方法较方法2在风电信号处理时不存在延时，具有更好的实时性；较方法1在满足国标所示风电并网要求的前提下，可以更好地获取风电并网功率，提高风电利用率，减少对储能的需求。根据图13c可知，未引入 GWO的ICEEMDAN在进行风电平抑时，存在难以全面获取风电并网功率信号的问题，风电并网功率过于平滑，弃风率较大，因此验证了引入 GWO算法优化ICEEMDAN的必要性。

4.2 混合储能系统功率分配效果分析

通过计算imf1～imf3信号之间的信息熵如表5所示，可以看出M=2时为出现的第一个极小值点，因此聚类分解出蓄电池功率为imf2+imf3，超级电容器功率为imf1。

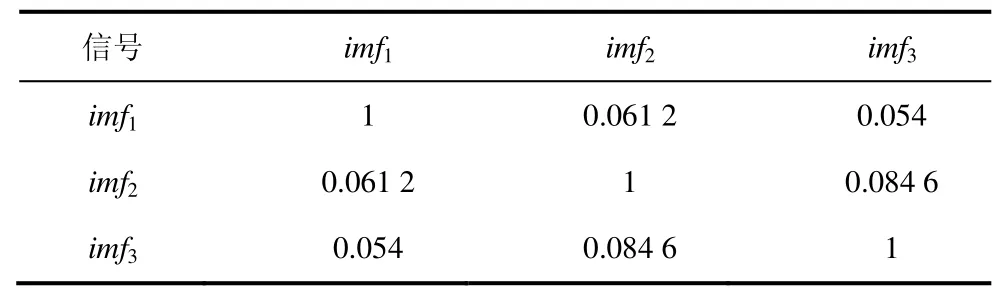
表5 各IMF分量的互信息

为避免储能SOC越限，采用模糊控制对采用信息熵确定的Ptg、Pcg进行修正，经过模糊控制优化的后储能功率和SOC状态如图14所示。

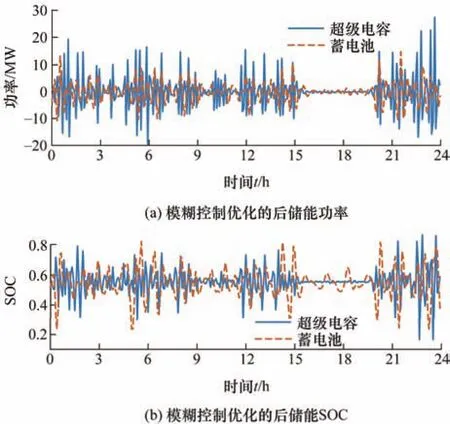
图14 模糊控制优化的后储能功率和SOC

通过图14可知，经过模糊优化控制的储能功率以及荷电状态均未出现越限现象，保证了储能介质处于正常的工作状态，极大提高了储能系统的使用寿命。

为了进一步验证 SOC模糊优化控制对储能SOC的调节能力，在极端情况将超级电容的初始荷电状态分别设置为30%和80%，对比分析有无模糊优化情况下超级电容的荷电状态如图15所示。

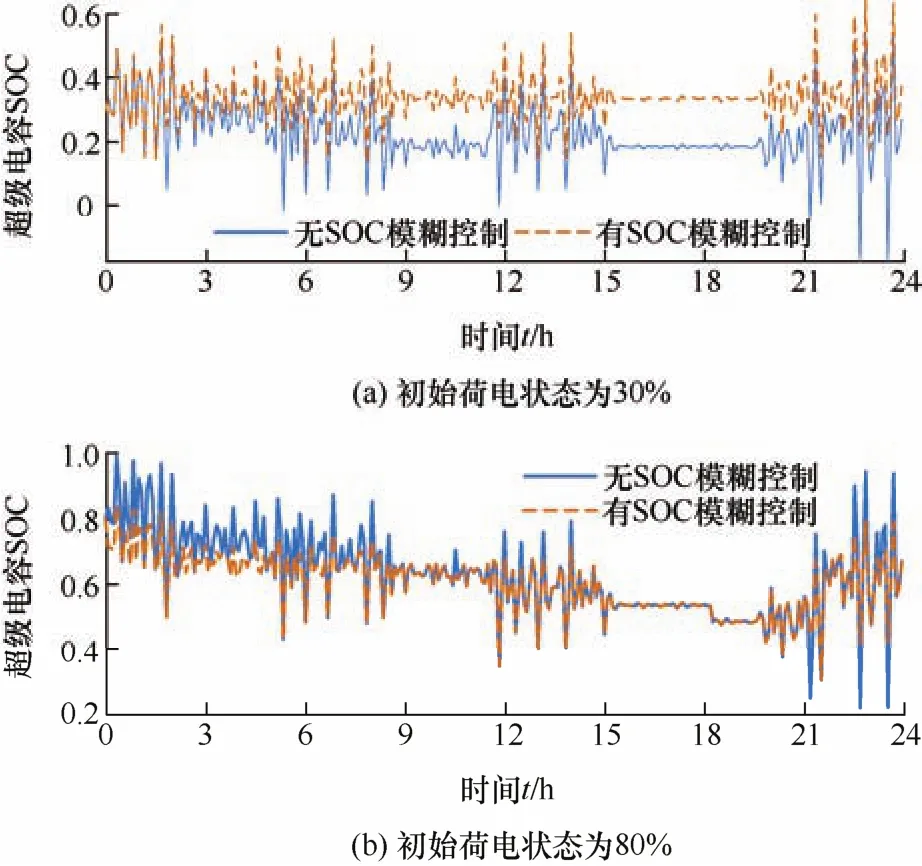
图15 有无模糊优化的超级电容SOC

由图15可知无模糊优化控制时，在极端情况下超级电容的SOC容易越限，而加入SOC模糊优化控制可以避免过充过放现象，证明了SOC模糊优化控制能够保证混合储能系统在极端情况下也能够满足风电平滑需求。

5 结论

为了满足风电并网要求，本文设计了一种采用灰狼算法优化改进的自适应噪声的完备集成经验模态分解的混合储能系统功率分配策略。为证明本文所述方法的有效性和优越性，从信号处理效果和SOC模糊控制效果进行对比分析，主要结论如下所述。

(1) 采用GWO-ICEEMDAN的信号处理方法，具有参数寻优速度快、不易陷入局部最优的优势，信号分解结果不易产生伪模态且噪声含量小，降低了风电并网功率获取难度。

(2) 通过信息熵结合模糊控制的混合储能系统功率分配方法，可以实现按照储能介质各自的性能特点分配功率，有效避免储能过充过放行为，提高混合储能系统的调节特性和运行经济性。

本文设计的控制策略是基于风电出力的历史数据，后续将进一步研究考虑风电的不确定性、储能布置方式等影响因素下的混合储能平抑风电波动控制策略。