LTD多间隙气体开关电场优化及自放率实验研究

降宏瑜，姜晓峰，王志国，孙凤举，魏 浩，楼 成，邱爱慈

(1. 强脉冲辐射环境模拟与效应国家重点实验室，西安 710024； 2. 西安交通大学 电力设备与电气绝缘国家重点实验室，西安 710049)

为满足Z箍缩惯性约束聚变点火及X射线强脉冲辐射环境模拟等研究的需要，迫切需建设电流数十兆安培、前沿百纳秒、功率数百太瓦的脉冲功率驱动源。快直线变压器驱动源(linear transformer driver, LTD)被公认为下一代大型脉冲功率源最有前景的新技术之一[1-9]，得到了世界上多个国家的广泛关注，研究人员开展了大量关键技术研究[1-10]。LTD可直接从直流充电电容器只经一级开关产生高功率快脉冲；采用模块化设计，结构紧凑，参数调整灵活；电容器充放电均为并联运行，电压叠加在次级实现，初级绝缘要求低，能提高脉冲驱动源的整体寿命与可靠性，具备重频运行潜力[2-4]。但大型LTD装置包含数万至十几万只气体开关，对气体开关提出了低自放电概率、低触发阈值、低抖动、低电感、高可靠及长寿命等要求[10]。其中，开关低自放电概率是装置稳定运行的前提，已成为 LTD 技术发展和工程应用的瓶颈。

近年来，国内外研究人员对于LTD气体开关技术开展了广泛研究，在气体开关工作机制、击穿特性、优化设计等方面形成了系列研究成果。关于气体开关自放电，研究了结构参数[11-13]、电极材料[14]、悬浮微粒[15-16]及表面形貌[17]等对开关自击穿特性的影响；通过开关间隙电场优化[18-19]、电极材料优选[20]及绝缘支撑优化设计[21]等提升开关特性；提出了一系列辅助措施降低气体开关自放率，如通过等离子体喷射触发实现开关低工作系数下触发导通[22]，采用电阻均压或电晕均压实现多间隙气体开关间隙电压均匀分配[23-25]等。

本文基于3维电磁仿真软件，采用有限元计算方法，仿真研究了环形电极倒角半径、截面参数和电极高度对气体开关间隙电场分布的影响，确定了优化的环形电极结构参数，并设计了4间隙串联气体开关。加工装配了3只样品气体开关，实验研究了单只气体开关击穿特性，并开展了万发次触发考核获得了开关自放率。批量试制了23只气体开关，分别测试了自击穿特性。将该批量开关应用于单级LTD模块，连续运行303发次，测试获得了模块自放率。

1 开关间隙电场优化

多间隙气体开关，是在正负极两端加电的高压电极之间，设置多个中间电极，将主间隙分隔为多个短间隙串联，电场分布比长单间隙电场分布更加均匀，可提升自击穿特性；单个间隙距离减小，且只有触发间隙工作在外触发状态，其他间隙在过电压下逐个击穿，可降低触发阈值[26]。此外，电极采用环形电极结构，利用触发间隙首先放电产生的紫外光，通过触发电极的中空通孔照射自击穿间隙产生初始电子，减小击穿抖动[27]。

本文在低电感3电极气体开关[28]基础上进行改进，采用4间隙串联结构，以降低开关自放率。开关间隙距离为6 mm，绝缘外壳外径为89 mm，内径为54 mm。环形电极外径为36 mm，其余结构参数，如内径、截面参数及电极高度等，根据电场仿真计算结果确定。

根据气体击穿理论，气体间隙中的电场分布是气体间隙击穿特性的主要影响因素。开关放电间隙的电场分布对开关的自击穿稳定性、触发闭合时延及抖动等性能都有决定性的影响[18]。在开关放电间隙结构设计中，一般将电场不均匀系数f作为主要参数，表示为[29]

(1)

其中：Emax为间隙最大电场强度；Eav为间隙平均电场强度，是间隙压降U与间隙距离d之比[13]。气体开关间隙一般采用稍不均匀的电场，如电场不均匀系数过大，击穿点过于集中，将会加剧电极局部区域的烧蚀程度，不利于延长开关的寿命，同时击穿电压偏低，需增加间隙距离来提高开关工作电压，使开关高度增加，电感增大；如电场不均匀系数过小，电场分布过于均匀，将降低间隙击穿电压稳定性[30]。因此电场不均匀系数f的选取，需在二者之间平衡，既能保证开关静态击穿电压的稳定性，又可延长开关的放电寿命。

1.1 环形电极倒角半径对间隙电场影响

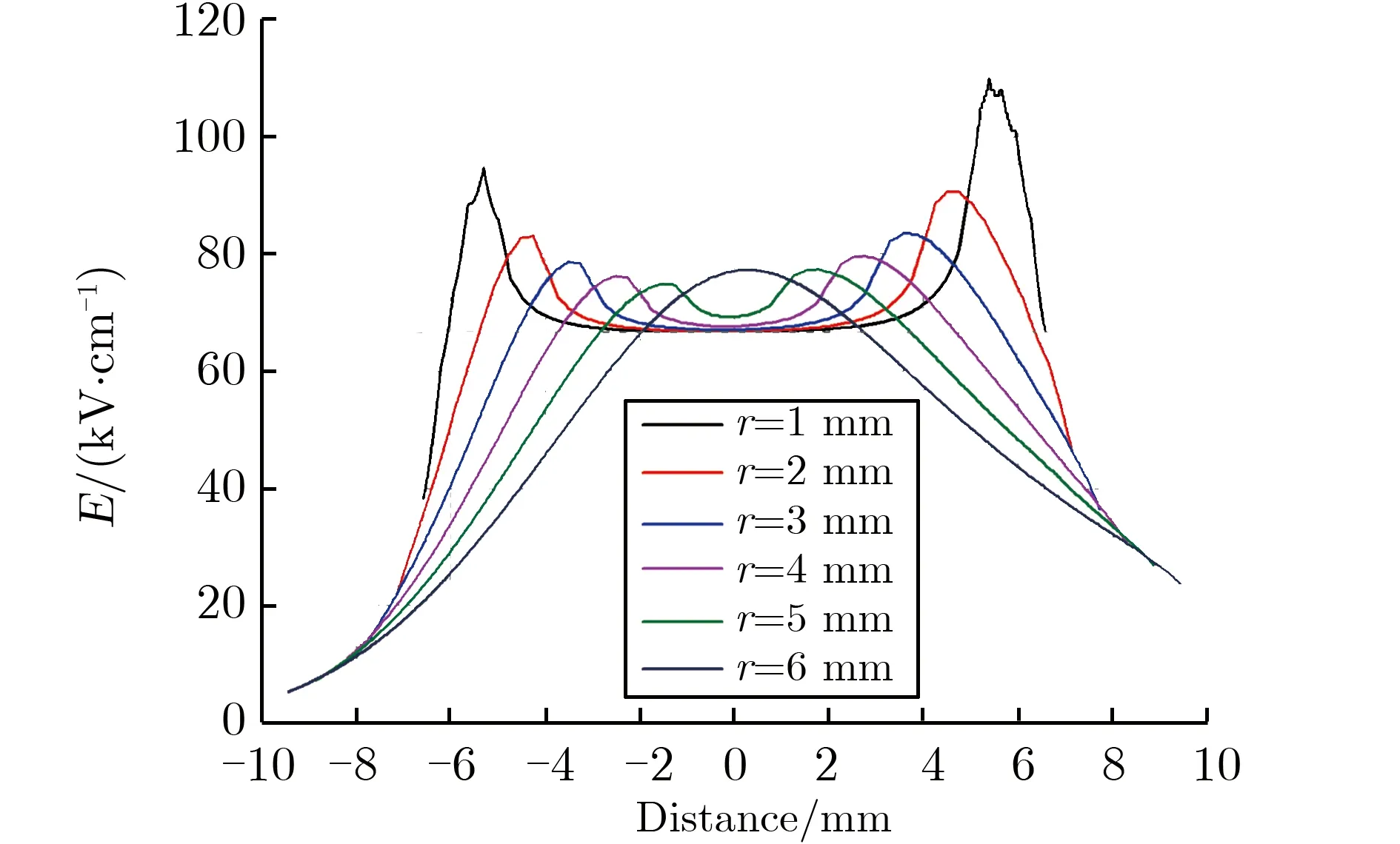
利用3维电磁仿真软件，建立环形电极计算模型。利用有限元计算方法，对不同倒角半径r的环形电极进行了静电场仿真分析，确定最佳倒角半径。设定环形电极内径为12 mm，倒角半径r分别为1,2,3,4,5,6 mm，其中，r=6 mm时，电极截面弧线部分为半圆形。上下两电极电位分别设置为40 kV和0。倒角半径不同时的环形电极间隙截面电场分布，如图1所示。

图1 倒角半径不同时的环形电极间隙截面电场分布Fig.1 Electric field distribution under different bend radius of ring electrode

其中，以下电极右半截面与间隙的分界线中点为0点，该分界线上与0点之间的长度为x，读取电极表面电场强度，分界线的终点为弧线部分做切线垂直于0点法向的点。

图2为倒角半径不同时间隙截面电场仿真计算结果。由图2(a)可见：受电极环形结构影响，0点左右两侧表面电场强度并不对称，电场强度最大处在0点右侧；随着倒角半径r的增大，电场强度最大处由倒角边缘逐渐向0点移动。

为定量描述电极表面电场集中的程度，定义电场集中系数c为

(2)

其中：lh为电极截面电场强度高于间隙平均电场强度的长度；lt为电极截面分界线两端终点之间的距离。c可一定程度上反映电极表面易放电的面积占比，作为选取间隙电场结构参数的参考。

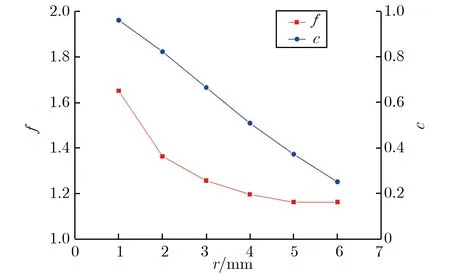
图2(b)为电场不均匀系数f和电场集中系数c随倒角半径r的变化关系。由图2(b)可见，f逐渐由1.62降低至1.16，c由0.9降低至0.25。r为5，6 mm时，f的值基本相等，但r为6 mm时，c值更小，有利于放电集中，降低放电分散性，故环形电极倒角半径r选为6 mm，即半圆截面。

(a) Electric field strength on surface

(b) f and c vs.r图2 倒角半径不同时间隙截面电场仿真计算结果Fig.2 Simulation results of gap electric field under the different bend radius

1.2 环形电极内径对间隙截面电场影响

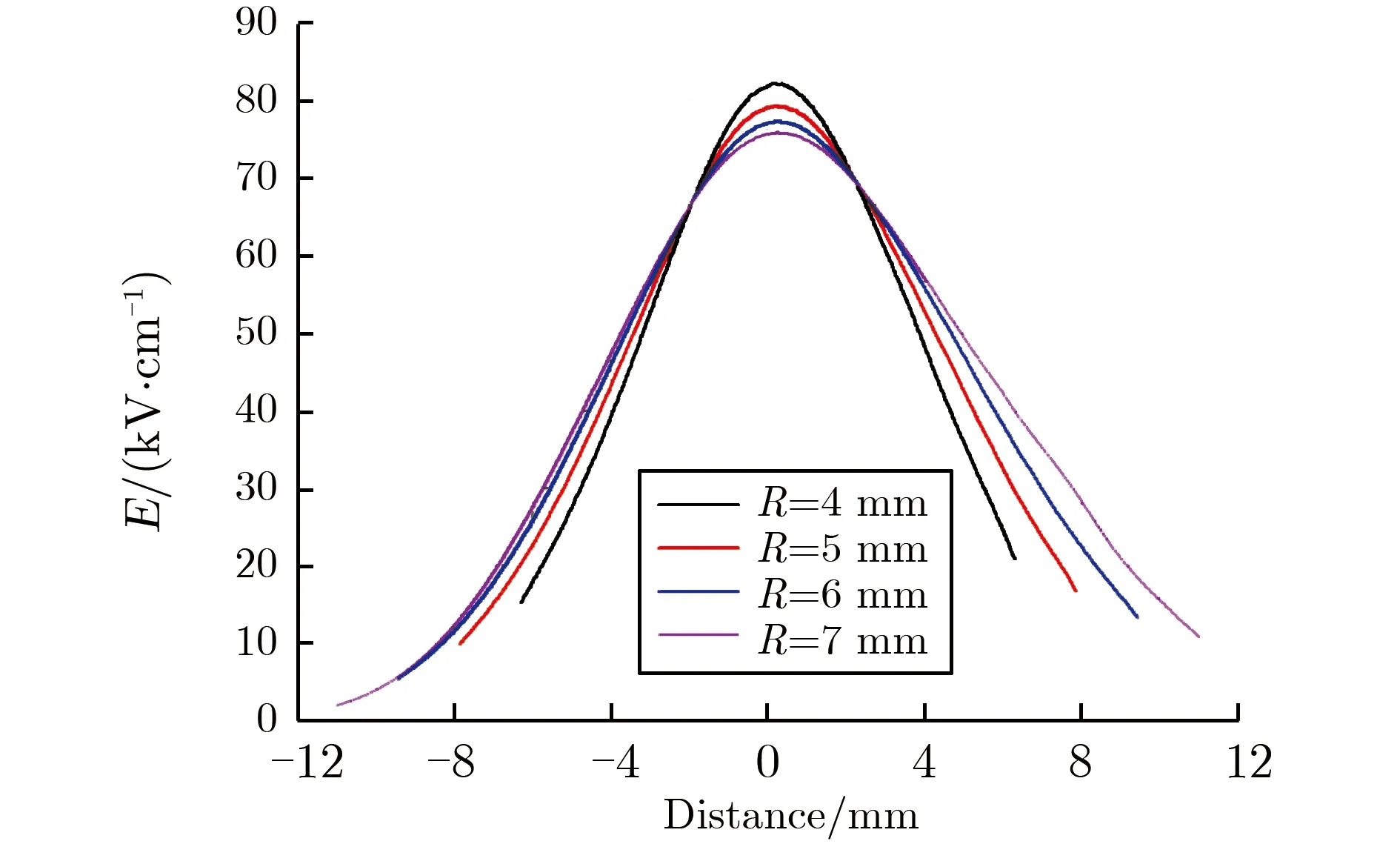
环形电极选用半圆截面，对不同内径下间隙截面电场强度进行了计算。半圆截面半径R分别取4，5，6，7 mm，此时环形电极内径依次为20，16，12，8 mm，不同半圆截面半径时的环形电极间隙截面电场强度分布，如图3所示。

图3 不同半圆截面半径时的环形电极间隙截面电场强度分布Fig.3 Electric field strength distribution under differenthalf-circle section radius of ring electrode

读取电极表面电场强度，计算了电场不均匀系数f和电场集中系数c。图4为不同半圆截面半径时的环形电极间隙截面电场仿真计算结果。由图4(a)可见，随着R的增大，f和c均减小，但R=7 mm时，环形电极中心通孔过小，不利于触发间隙产生的紫外光透射到自击穿间隙，故R值选定为6 mm，即环形电极内径为12 mm。

(a) Electric field strength on surface

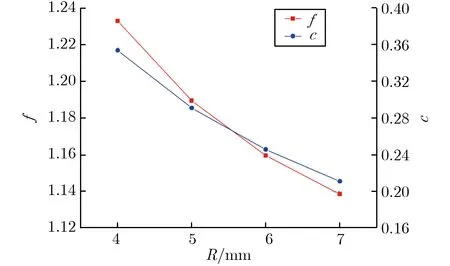
(b) f and c vs.R图4 环形电极不同半圆截面半径下间隙截面电场仿真计算结果Fig.4 Simulation results of gap electric field under the different half-circle section radius of ring electrode

1.3 环形电极截面参数对间隙截面电场影响

在确定环形电极内径的基础上，将半圆截面改为椭圆截面，进一步改善电场分布。椭圆截面长半径a为6 mm保持不变，短半径b为2～6 mm时，进行电场仿真，其中b为6 mm时为半圆截面。短半径不同时环形电极椭圆截面的间隙截面电场分布，如图5所示。短半径不同时环形电极椭圆截面的间隙电场仿真计算结果，如图6所示。计算f与c时，b的间隔取0.2 mm。由图6(a)可见，短半径b为2 mm时，电场强度最大处在截面边缘。由图6(b)可见，随着短半径b的增大，f由1.06逐渐增大至1.16，c由0.44逐渐降低至0.25。截面参数的选取，需平衡f与c的值，故选定短半径b为3.8 mm，此时f为1.11，c为0.34。

图5 短半径不同时环形电极椭圆截面的间隙截面电场分布Fig.5 Electric field distribution under different elliptic section short radius of ring electrode

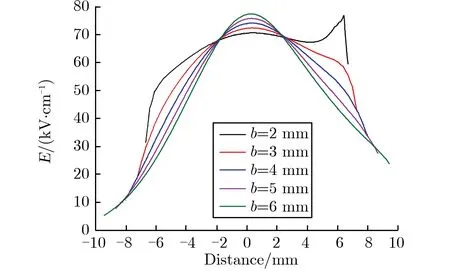
(a) Electric field strength on surface

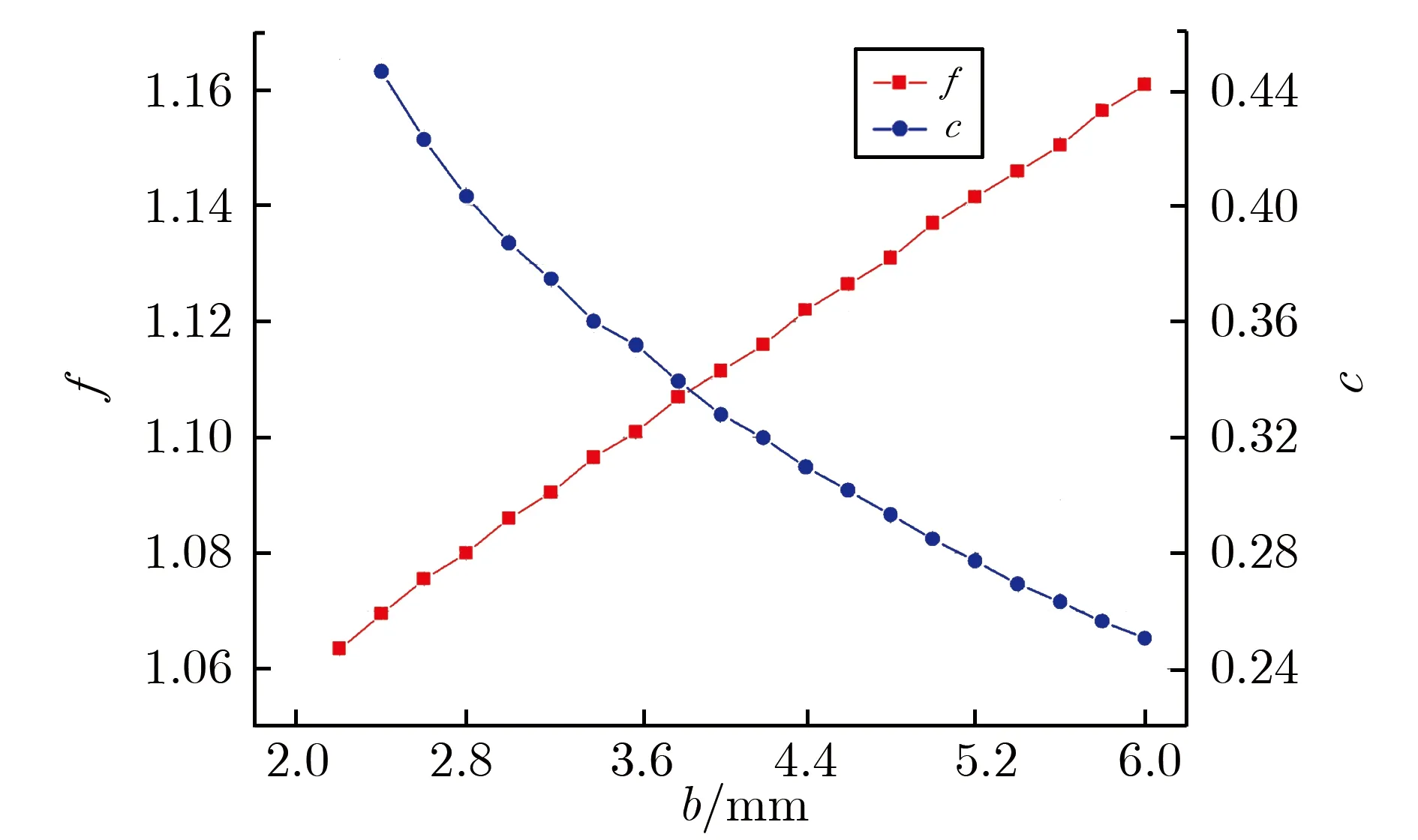
(b) f and c vs.b图6 短半径不同时环形电极椭圆截面的间隙电场仿真计算结果Fig.6 Simulation results of gap electric field under the different elliptic section short radius of ring electrode

1.4 环形电极高度对开关间隙截面电场分布影响

在开关整体高度不变，间隙距离确定的情况下，电极高度将影响开关各间隙的电压分配，因此，需根据开关整体结构的电场仿真结果选取。建立4间隙气体开关3维电磁模型，上下高压电极电位设定为±80 kV，触发电极设定为地电位，两个中间电极电位悬浮，电极高度h分别为21,23,25,27,29 mm，进行电场仿真。其中，h=23 mm时开关截面电场分布如图7所示。电极高度不同时，开关间隙截面电场强度如图8所示。

图7 h=23 mm时开关截面电场分布Fig.7 Electric field strength distribution of switch at h=23 mm

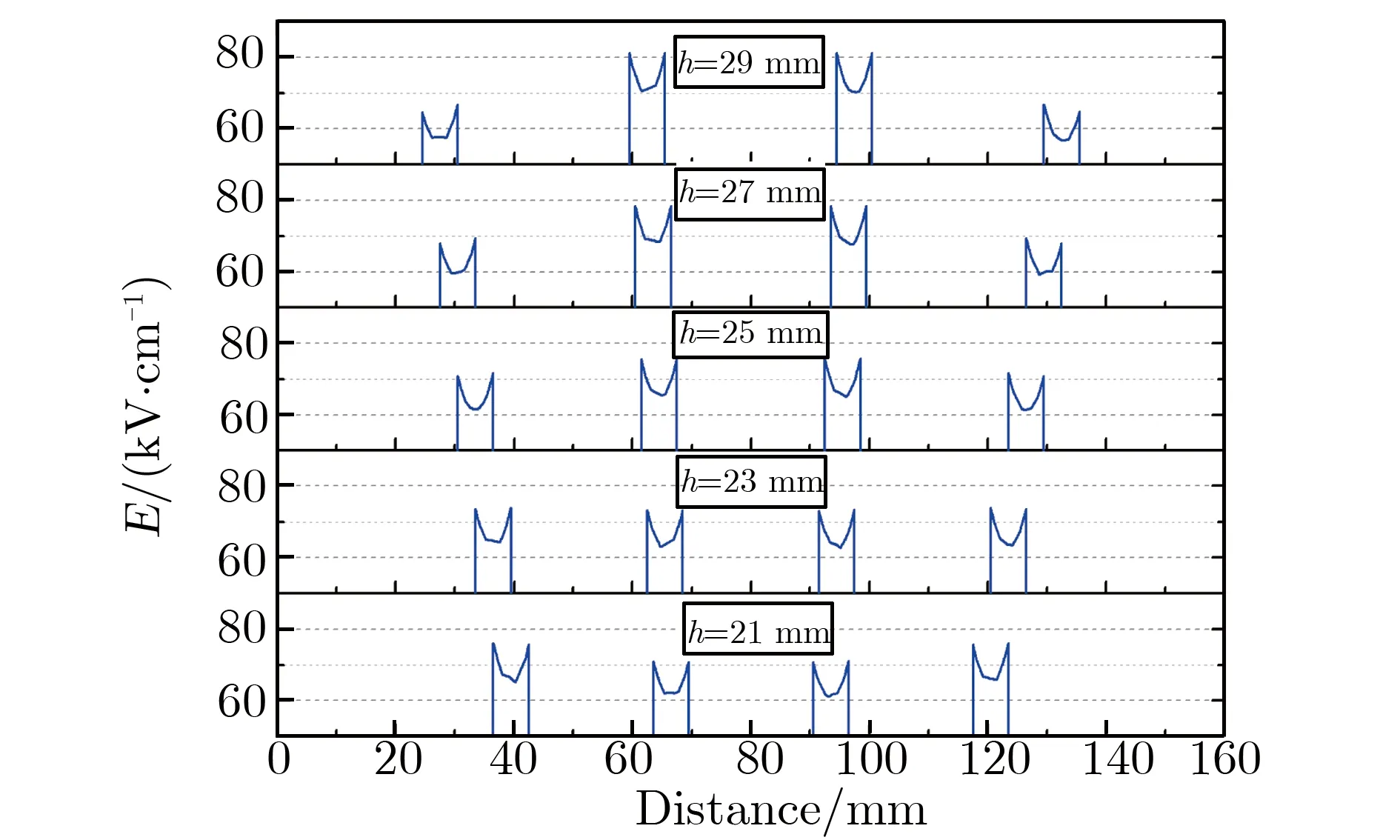
图8 电极高度不同时，开关间隙截面电场强度Fig.8 Electric field strength of switch gap under different h

为定量描述开关各间隙截面电场强度分布的差异，定义电场强度差异系数δ为

(3)

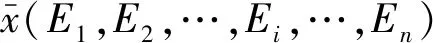
电极高度h分别为21，23，25，27，29 mm时，计算得到电场的差异系数δ分别为0.039，0.005，0.034，0.076，0.122。由此可见，电极高度h为23 mm时，间隙电压均匀分配，利于提升开关自击穿特性。

2 4间隙气体开关设计

依据电场仿真结果，确定环形电极的外径为36 mm，内径为12 mm，高度为23 mm，椭圆截面短半径为3.8 mm，设计了4间隙气体开关，图9为开关剖面图。开关整体为圆柱形，外径为89 mm，高度为152 mm。绝缘外壳为圆筒形，中平面开有1个触发连接孔和1个充放气孔。位于中平面的触发电极和2个中间电极通过3个绝缘柱，顶在外壳内壁的圆弧坑里。上下高压电极分别通过8个螺钉和2个卡环配合紧固在绝缘外筒两端，主电极与绝缘外壳之间装有密封圈。箍环将开关固定在放电支路电容器上。触发电极通过触发杆与触发电缆连接。电极采用不锈钢，箍环材料采用铝合金，绝缘外壳采用有机玻璃，其余绝缘件材料为尼龙。

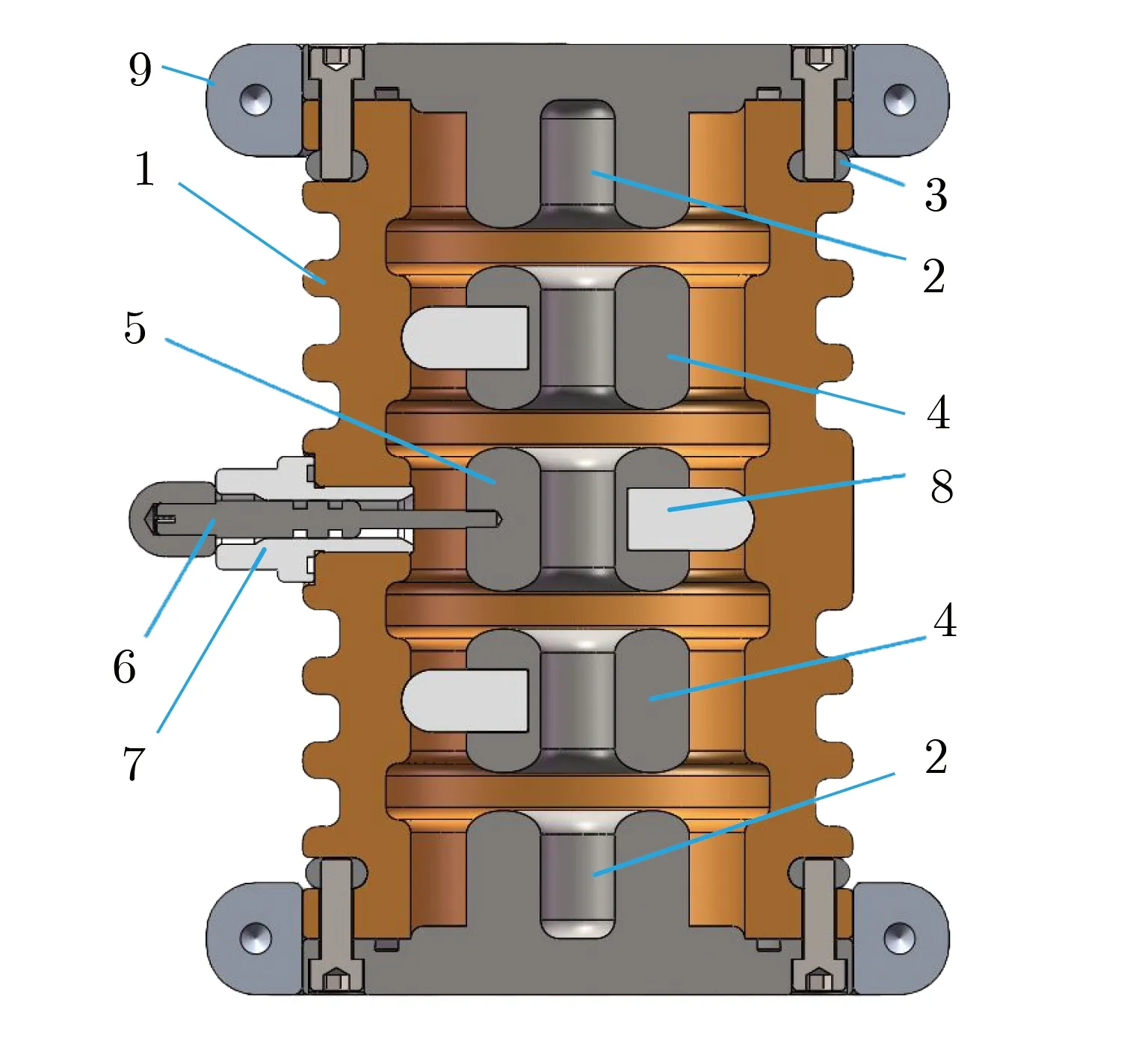
1- insulation shell；2-high-voltage electrodes；3-snap ring；4-intermediate electrode；5-trigger electrode；6-trigger rod；7-trigger connector；8-insulating post；9-hoop图9 4间隙气体开关剖面图Fig.9 Cutaway view of the four-gap gas switch

3 气体开关击穿特性实验

3.1 气体开关实验平台

单只开关的击穿特性实验在高功率气体开关特性实验平台[20,28]开展，采用功率为5.8 GW的放电支路，包含2只±100 kV/100 nF电容器和1个低电感水电阻负载，模拟气体开关在模块中的实际工况，气体采用0级空气。在充电电压为±80 kV时，开关触发电压和放电电流波形如图10所示。由图10可见，触发波形峰值为160 kV，前沿为15 ns，支路放电电流峰值为48 kA。延时tdelay定义为触发电压起始时刻与放电电流起始时刻之差，抖动tjitter定义为50发触发实验延时的标准偏差[20]。

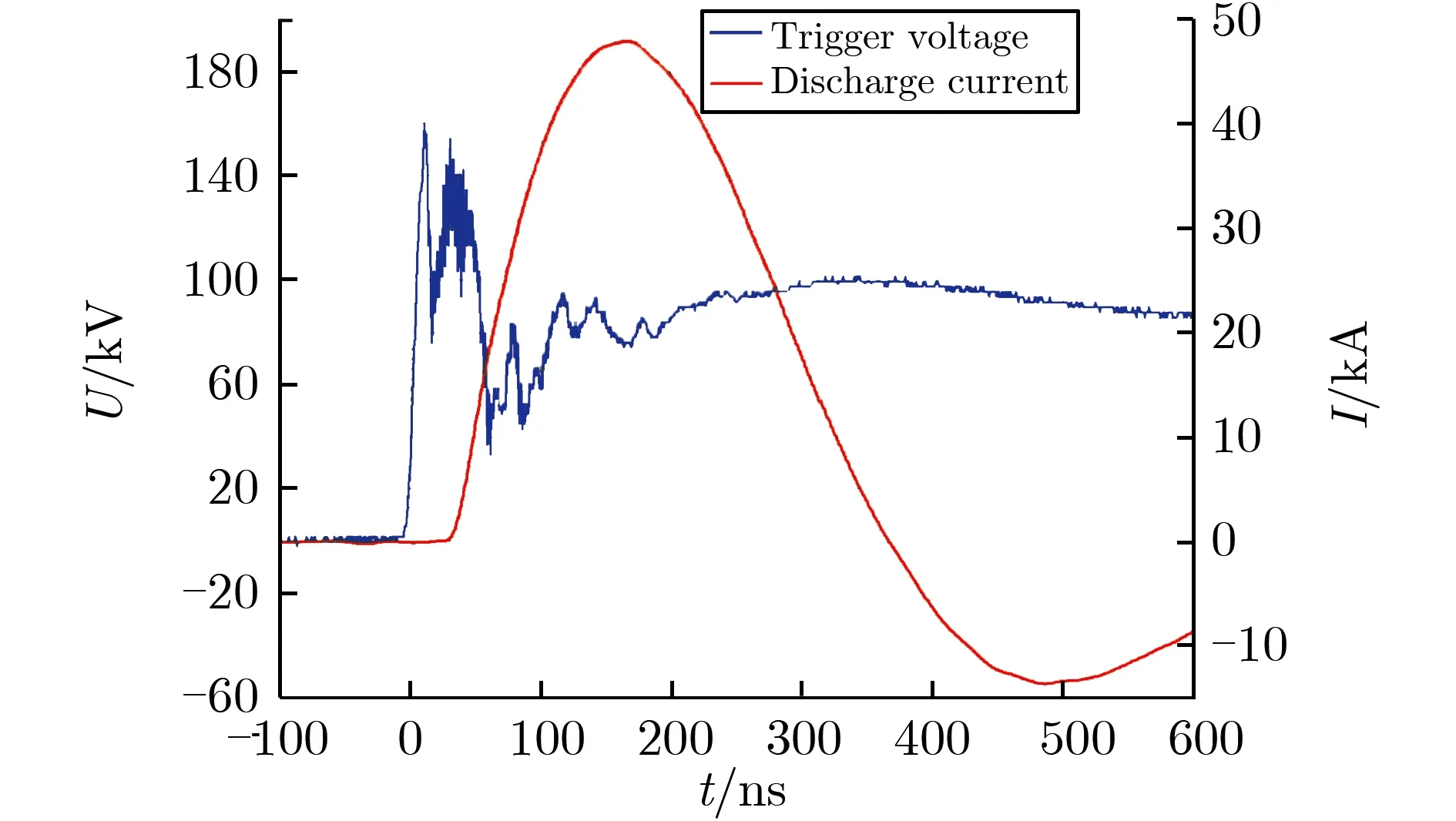
图10 当充电电压为±80 kV时开关典型触发电压与放电电流波形Fig.10 Typical waveforms of the discharge current and the trigger voltage when the charging voltage is ±80 kV

3.2 样品开关击穿特性

加工装配了3只样品开关，均在气压p为0.3 MPa下老练500发，该气压下开关自击穿电压Ub约为±90 kV。测试了开关在气压为0.17，0.21，0.26，0.29 MPa下的自击穿特性，如图11所示。其中自击穿电压Ub为50发的平均值。由图11可见，3只气体开关自击穿特性一致性较好，自击穿电压Ub随气压p的增加保持线性增加关系，由拟合曲线可得开关自击穿电压Ub与充气气压p的关系为

Ub=37.86+495.7p

(4)

式(4)中，当p为0.26，0.29 MPa时，3只开关自击穿电压Ub为170 ，180 kV，标准偏差均小于4 kV，分散性(标准偏差与自击穿电压之比)小于3%。

图11 不同气压下开关的自击穿特性Fig.11 Self-breakdown characteristics of switches under different air pressures

开关在工作电压为±80 kV时，进行了触发电压为160 kV，工作系数分别为0.65，0.70，0.75，0.80时的触发实验，开关工作系数定义为

(5)

其中，U为气体开关的工作电压。因此当开关工作系数确定时，对应的气压p可由式(4)与式(5)计算得到。图12为开关延时及抖动随工作系数的变化关系。由图12可见，开关的抖动小于3 ns。

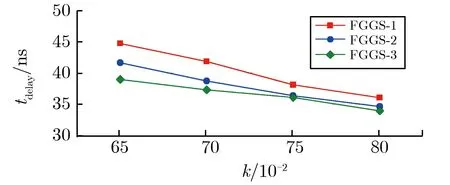
(a) tdelay vs. k

(b) tjittervs. k图12 开关延时及抖动随工作系数的变化关系Fig.12 Switching delay and jetter vs. working coefficient

开展气体开关10 000次触发考核测试其自放率。在工作系数为0.70时，触发10 321，9 906，10 027发，得到开关触发考核延时如图 13所示。由图13可见，3只开关的延时分别为42.6，37.1，37.5 ns，抖动分别为2.08，1.77，1.75 ns，发生自放的次数分别为0，2，3次，开关自放率小于0.03%。

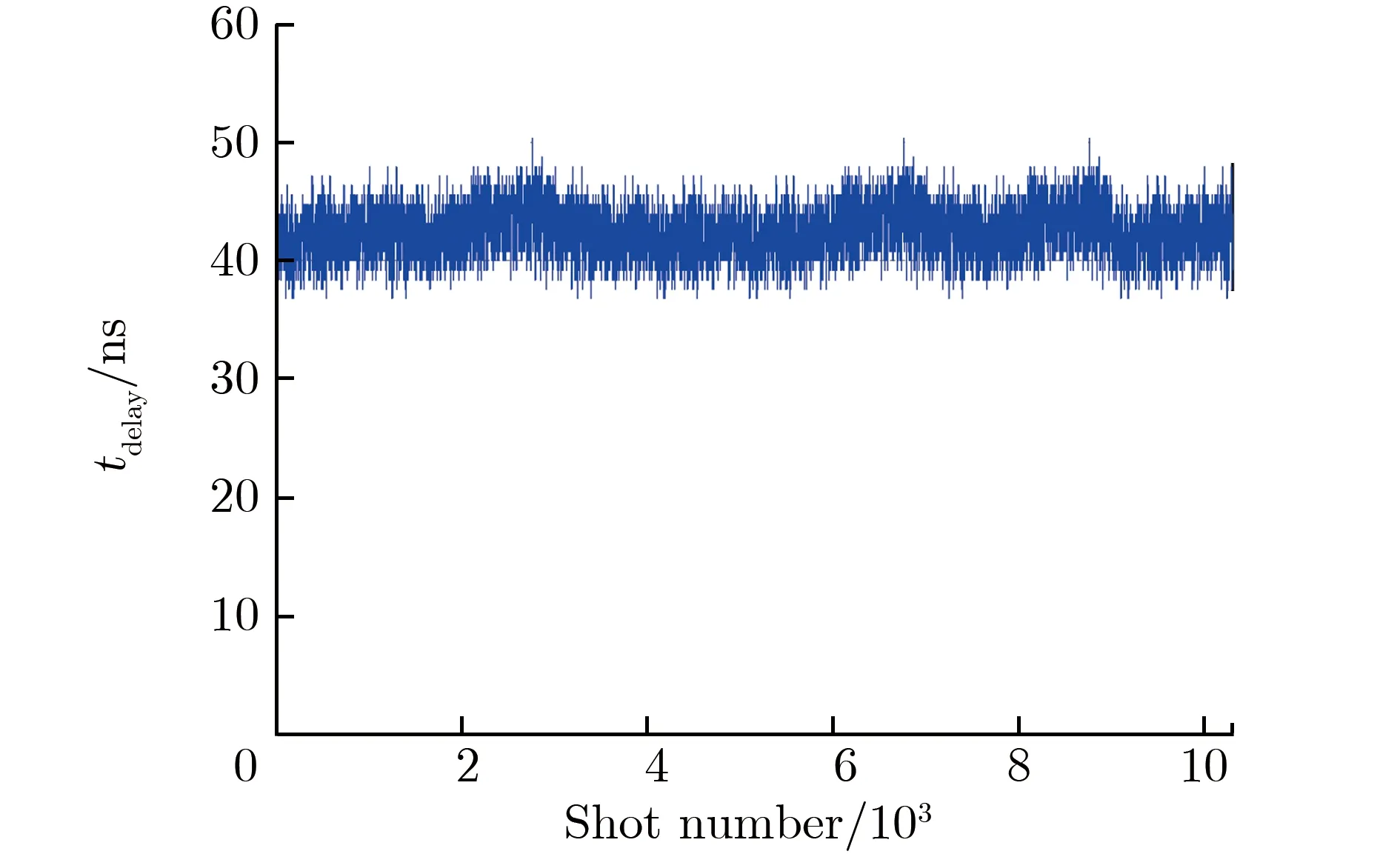
(a) FGGS-1

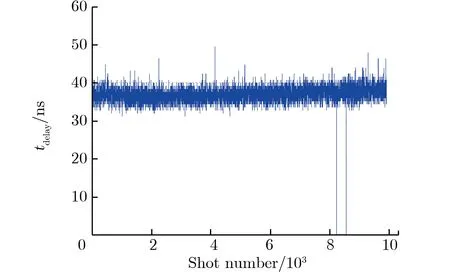
(b) FGGS-2

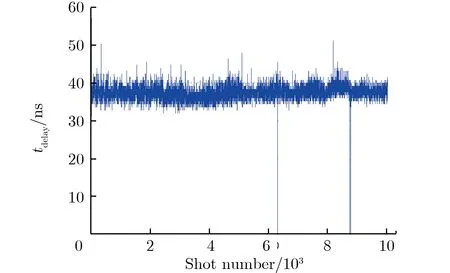
(c) FGGS-3图13 开关触发考核延时Fig.13 Delay time vs. shot number during triggering test

3.3 批量开关自击穿特性

批量试制了23只开关，与前述自击穿特性测试步骤相同，分别进行老练500发后，测试不同气压下的自击穿特性。批量开关在气压为0.26 MPa时自击穿电压及分散性，如图14所示。

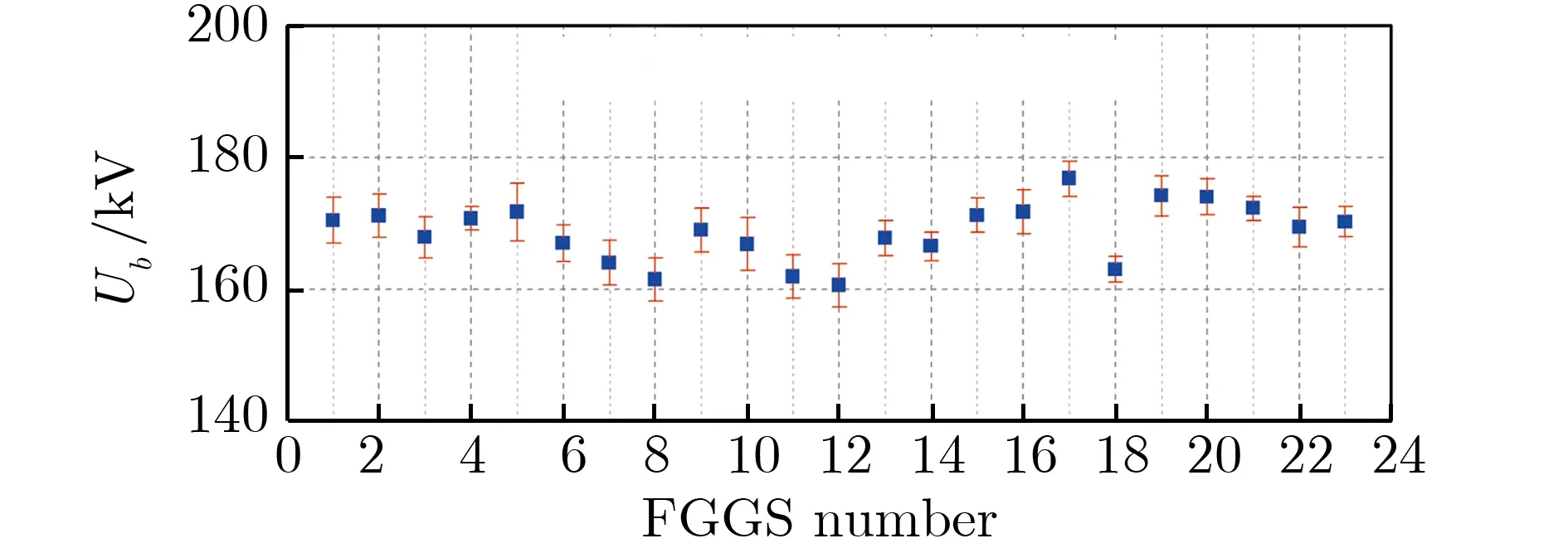
(a) Ub

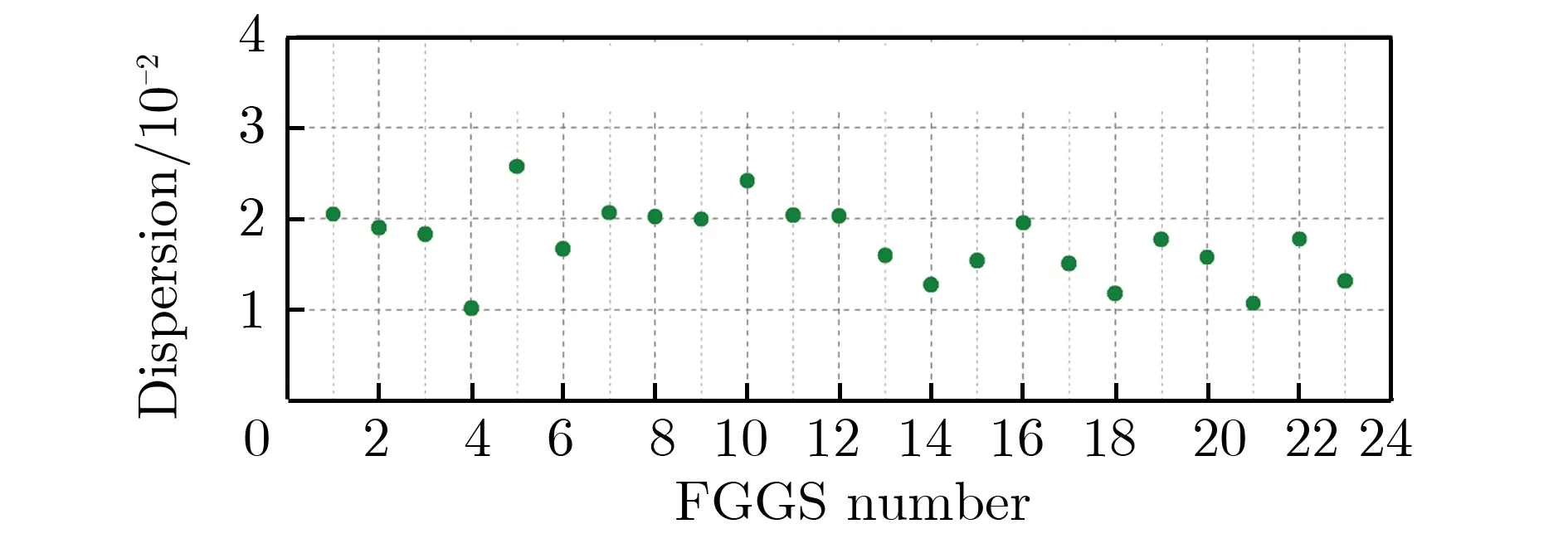
(b) Dispersion图14 批量开关在气压为0.26 MPa时自击穿电压及分散性Fig.14 Self-breakdown voltage and dispersion of batch switch at p=0.26 MPa

由图14可见，23只开关自击穿电压Ub并不完全一致，这由于批量加工装配具有固有偏差，Ub最大值为176.8 kV，最小值为160.6 kV，平均值为168.7 kV，标准偏差为4.3 kV。每只开关的自击穿电压分散性均小于3%。

4 单级模块实验

将经过老练和测试的23只开关安装于兆安量级气体绝缘单级LTD模块[8]，分别与2只100 nF塑壳电容器组成主放电支路。图15为兆安量级气体绝缘单级LTD模块示意图。模块直径d为2 290 mm，高度为346 mm，初级腔体采用SF6气体绝缘。24个放电支路沿圆周轮辐状布置，其中23个支路为主放电支路，1个支路为触发支路。图16为4间隙气体开关安装于LTD模块中的实物图。主放电支路开关从1#到23#编号。

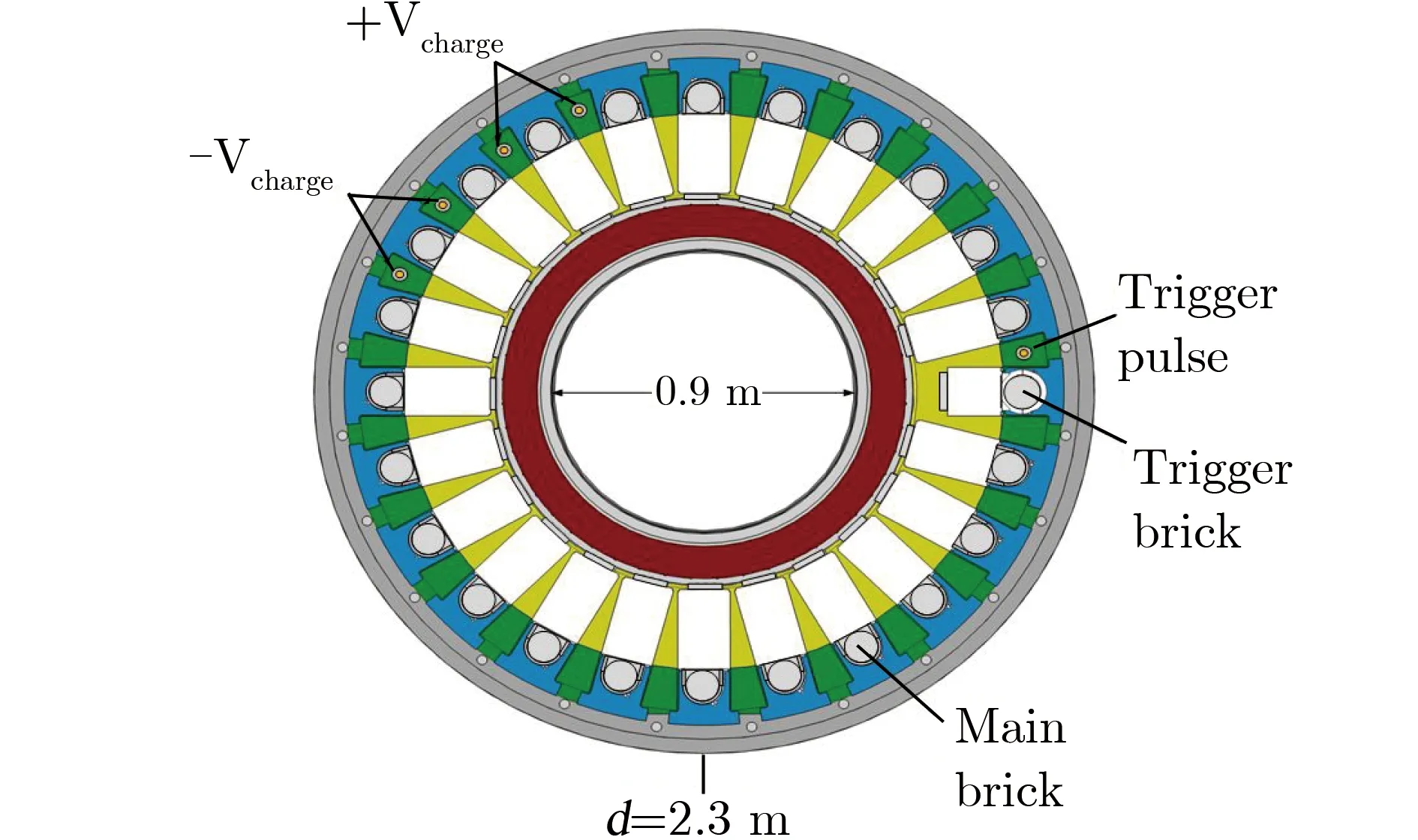
图15 兆安量级气体绝缘单级LTD模块示意图Fig.15 Gas-insulated mega-ampere-class LTD module

图16 4间隙气体开关安装于LTD模块实物图Fig.16 Four-gap gas switch installed in LTD module

模块充电电压为±80 kV，工作系数为0.65，充电完成耐压3 s后触发，每发更换气体，每3发去磁，连续运行303发，每发放电负载电流峰值如图17所示。

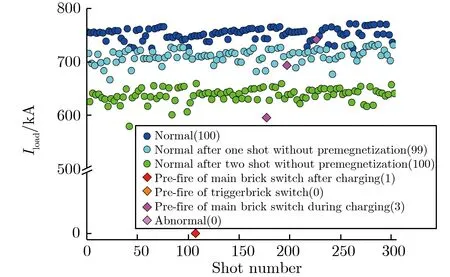
图17 模块连续运行303发负载电流峰值Fig.17 Peak load current during continuous operation of 303 shots

模块工作状态共7种，分别是：(1)去磁后正常触发100发；(2)去磁后第2发正常触发99发；(3)去磁后第3发正常触发100发；(4)主支路气体开关充电过程中自放1发；(5)触发支路气体开关自放0发；(6)主支路气体开关充电完成耐压过程中自放3发；(7)其他异常0发。其中，前3种状态是模块正常发次，共299发。模块第107发在升压过程中自放，自放开关为18#，第177，197，226发耐压1 s以上自放后正常触发，自放开关分别为12#，4#，23#，可见4次开关自放电是随机出现的，测试得到模块自放率为1.32%。

如模块中气体开关发生自放电是独立事件，则模块的自放电概率PLTD表示为

PLTD=1-(1-Pswitch)n

(6)

其中，Pswitch为开关自放电概率；n为模块中开关个数，对于本模块n=23。若Pswitch等于开关万发次考核的自放率0.03%，则计算得到模块在工作系数为0.7时，自放电概率PLTD=0.69%。工作系数为0.65时，自放电概率理论上应比0.69%更小，但实测为1.32%。模块自放率实测值比计算值偏大，一方面可能的原因是模块中开关自放电为非独立事件，存在相互耦合的因素，另一方面也可能由于开关在充电完成后的耐压时间较长，导致开关自放率升高。

5 结论

本文开展了气体开关间隙电场仿真研究，分析了环形电极倒角半径、电极内径、椭圆截面短半径及电极高度对间隙电场分布的影响，通过读取电极表面电场强度，计算出电场不均匀系数和电场集中系数，平衡二者的值。降低电场差异系数，确立了优化的环形电极结构参数。

研制了4间隙气体开关，工作电压为±80 kV，工作系数为0.70时，单只开关自放率小于0.03%；自击穿电压为±80 kV时，批量23只气体开关分散性均小于3%；充电电压为±80 kV，工作系数为0.65时，LTD模块连续运行303发次，模块自放率为1.32%。

下一步计划对LTD模块进行更多发次的测试考核，给出更多发次实验下的自放率，同时开展批量开关击穿特性一致性研究，用于制定气体开关筛选标准规范，为LTD大批量气体开关的应用奠定基础。