基于Jiles-Atherton模型的四级串联FLTD电路仿真

万臻博，丁卫东，何 旭

(西安交通大学 电力设备电气绝缘国家重点实验室，西安 710049)

快脉冲直线变压器驱动源(fast linear transformer driver ,FLTD)被国内外高功率脉冲领域视为Z箍缩驱动源最具有前景的技术路线，是未来数十兆安Z箍缩惯性约束核聚变研究的重要基础。目前，国内外对FLTD的单模块、多级串联装置及基于FLTD多路并联的大型Z箍缩驱动器的概念设计已展开了诸多研究[1-6]。与此同时，数值仿真方面也有了较多进展[7-13]。作为FLTD电压和功率叠加的重要器件，磁芯的有效建模对正确反映FLTD输出特性十分重要。目前，国内外的FLTD仿真中对磁芯模型的研究仍比较欠缺，大多数的仿真研究将磁芯等效为定值电感或固定磁导率的介质来处理，如，美国圣地亚国家实验室使用的LSP 3维粒子仿真[9]及西安交通大学使用Pspice电路模拟中[11-12]，关注了磁芯从完全去磁的反向饱和状态到正向饱和状态之间的非线性过程，即考虑了一部分磁化曲线，但不具备磁滞回线的特征。当前大部分数值仿真主要针对FLTD正常工况的输出特性，正常工况下各级模块的磁芯励磁方向一致，且不易饱和。与主电流相比，磁芯回路中的励磁电流，即，FLTD的漏电流非常小，因此，对整体输出电压和电流等参数的模拟基本无影响，仿真与实验结果符合较好。然而，在FLTD的开关自放电等异常工况下，由于各级磁芯励磁方向不统一，磁芯的励磁状态会对FLTD各个位置的输出电压和电流波形产生很大影响，因此，研究磁芯在FLTD中的工作模式，改进磁芯等效模型有助于更好地模拟和预测FLTD故障波形，对FLTD调试、实验和故障诊断具有重要意义。

本文主要将Jiles-Atherton(J-A)磁滞模型与四级串联FLTD的电路模型耦合，在FLTD电路模型中引入磁滞回线的作用，提高电路模型对FLTD的自放电等故障特征波形的模拟准确性，并结合已建成的四级FLTD平台的实验波形进行验证。

1 磁芯等效模型的建立

1.1 J-A磁滞模型

J-A模型从磁性材料磁化的物理角度，推导了材料磁化过程中磁化强度M与磁场强度H之间的关系，模型简单，物理意义明确，得到了广泛应用[14-16]。文献[15]给出了J-A模型的具体推导过程。J-A原模型可表示为

He=H+αM

(1)

(2)

(3)

模型包含Ms,a,α,c,k5个主要参数，其中：Ms为最大磁化强度，决定了材料的最大磁感应强度Bm；a和α分别为有效磁畴密度和磁化耦合系数，主要影响材料磁化退磁化的难易程度，在磁滞回线中决定了剩磁点的位置；c,k分别为可逆磁化系数和能损参数，主要决定了磁化过程中磁滞损耗的大小，在磁滞回线中对应了矫顽力的大小；δ为方向系数，当磁场强度的变化率大于0时，取+1，反之取-1；Man,Mirr分别为无磁滞的磁化强度和不可逆磁化强度；H为磁场强度；M为总磁化强度；He为有效磁场强度。通过在磁化方向改变时引入系数ξ将不可逆磁化分量Mirr置0来除去J-A原模型相对磁导率为负值的非物理解。最终采用的模型可表示为

(4)

(5)

1.2 磁滞回线测定与参数识别

尽管文献[16]给出了J-A模型参数的实验获取方法，但实际应用较为困难，目前，常用的参数识别方法是通过模拟退火算法、遗传算法及粒子群算法等自动寻优算法来拟合实验磁滞回线[17-19]。由于J-A模型表征的是磁性材料的静态磁滞特性，在测定磁滞回线时应采用静态或低频准静态激励，减少动态损耗对模型参数识别的影响。本文采用1 Hz低频正弦激励。待测的磁芯样品为2605SA1非晶磁芯，材料和制作工艺与FLTD所使用的磁芯完全一致，外径为300 mm，内径为100 mm，高为70 mm，有效截面积为46.95 cm2，平均磁路长度为62.52 cm，最大磁感应强度Bm大于1.45 T，剩磁Br大于1.35 T，最大伏秒数约为15 mV·s-1。由信号发生器产生1 Hz正弦波，经功率放大器放大后施加在磁芯上，逐渐增大放大倍率直至磁芯达到完全饱和，在原边线圈中串联采样电阻采集励磁电流波形，在副边使用电压探头直接测量线圈开路电压，为使磁芯饱和时励磁电流不至于过大且副边电压具有足够的信噪比，原、副边的线圈匝数分别为30和18，磁滞回线的测量回路如图 1所示。根据电磁感应定律，对副边电压积分即可得到磁通密度B，表示为

(6)

其中：n为副边线圈匝数；S为磁芯有效截面积；U2为副边感应电压；T为时间；B0为0时刻的磁通密度。

根据安培环路定理，由原边电流可得到磁场强度H，表示为

(7)

其中：N为原边线圈匝数；l为磁芯平均磁路长度；Im为原边励磁电流。

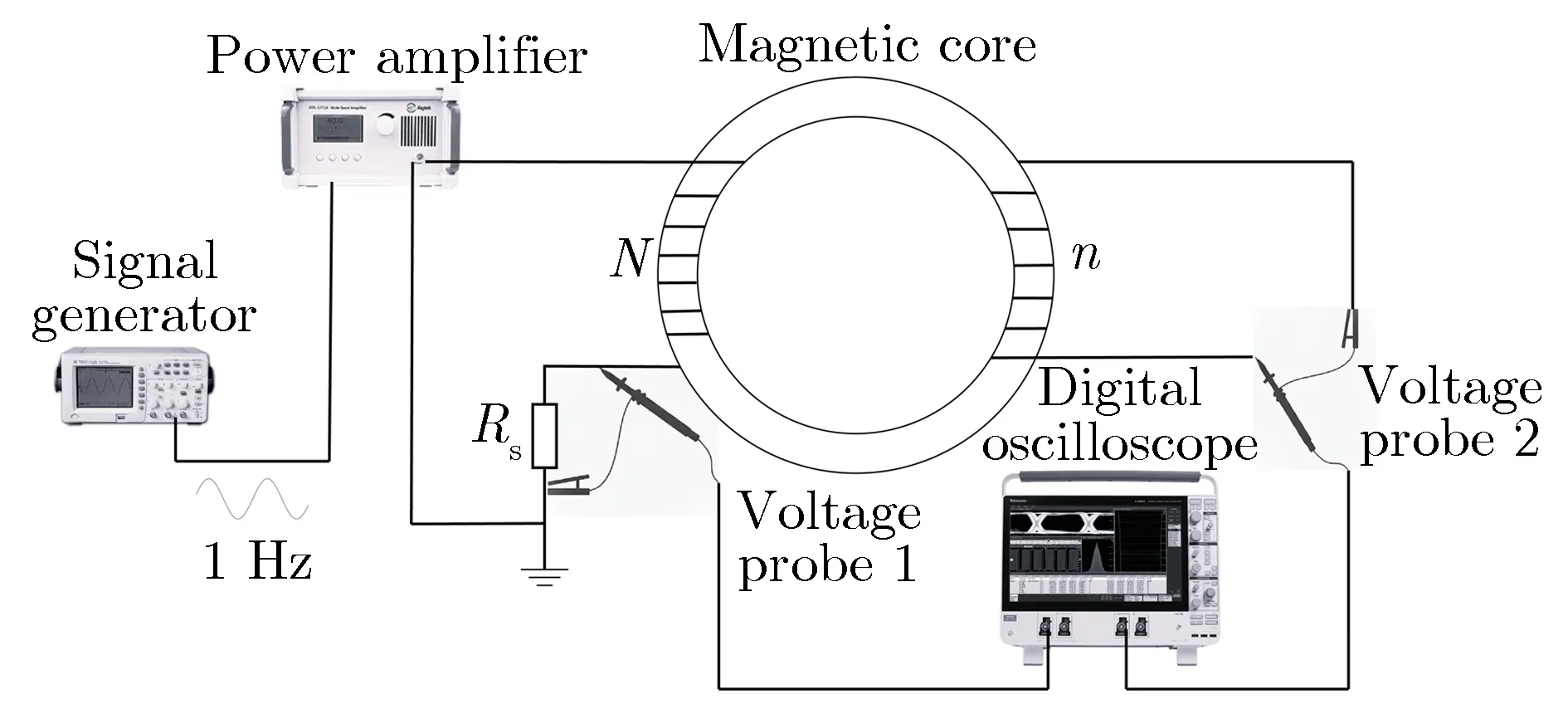
图1 磁滞回线测量回路Fig.1 Measuring circuit of hysteresis loop

将实验采集的磁场强度H作为自变量，通过J-A模型计算出对应的磁感应强度，以实验测得的磁感应强度与J-A模型计算值之差的均方根作为优化函数，使用粒子群算法进行拟合，最终得到的J-A模型参数及拟合磁滞回线分别如表1所列和图2所示。

表1 J-A模型参数Tab.1 Parameters of J-A model

图2 实验测量与拟合的磁滞回线对比Fig.2 Comparison of measured and optimized hysteresis loop

1.3 磁芯等效电路模型

根据损耗分离的思想，采用一个电感和一个电阻的并联支路来等效磁芯的作用。电感表征与频率无关的静态磁滞损耗；电阻表征动态涡流损耗的影响，由于在FLTD特征激励下，涡流损耗趋肤深度远大于磁芯带材25 μm的厚度，因此忽略因趋肤效应导致的损耗电阻变化，简化为定值电阻。电感L和电阻Re可表示为[20]

(8)

(9)

其中：μ0为真空磁导率；μr为磁芯相对磁导率；ρcore为磁芯材料电阻率；d为磁芯带材厚度；rcore为磁芯半径；t为电流峰值时间。由式(9)计算可得，磁芯等效涡流损耗电阻约为45 Ω。

2 四级FLTD电路计算模型

移除了外壳的四级串联FLTD内部结构如图 3所示。每级模块包含了23个由2个100 kV、100 nF电容和1个场畸变气体开关构成的主放电支路及一个触发支路，次级为变阻抗的水介质传输线[20]。四级FLTD的电路模型如图4所示，主要由放电支路、磁芯支路和次级传输线3部分构成。

模型主要关注级间输出特性，因此忽略了每级模块中开关闭合的分散性，将一个模块中的23个并联主支路简化为一个RLC串联支路考虑。将变阻抗水传输线简化为四段定值阻抗的传输线，在电路中分别由8个LC人工传输线单元模拟。电路中其他相关参数如表 2所列。

图3 四级串联FLTD的内部结构Fig.3 Internal configuration of the four stages FLTD module

图4 四级FLTD电路模型Fig.4 Circuit model of the four stages FLTD module

表2 FLTD电路模型参数Tab.2 Parameters of the FLTD circuit model

求解电路时，首先将所有的储能元件的瞬态模型离散化得到计算电路。储能原件瞬态离散模型如图5所示。此时电路中只包含了导纳元件和独立电流源，采用节点法求解电路的线性方程组，即可得到下一时刻所有的节点电压和电感支路的电流，利用离散的运算电路避免了微分方程组的求解，计算效率大大提高。

图6为含时变磁芯电感的瞬态电流求解流程图。根据磁芯支路的励磁电流和励磁电感两端的电压计算下一时刻磁芯的磁场强度、磁感应强度和磁化方向，再代入J-A模型更新磁芯励磁电感的大小。由此按照一定的时间步长反复迭代即可得到电路中各个位置处节点电压的时域波形。

图5 储能元件瞬态离散模型Fig.5 Transient discrete model of energy storage elements

图6 含时变磁芯电感的瞬态电流求解流程图Fig.6 Flow chart for solving transient current with time-varying core inductance

3 FLTD输出特性的实验与模拟结果

3.1 正常时序触发时各级电压波形

FLTD一般会采用理想IVA时序进行触发，以获得最佳的电压和功率叠加效果，即前级的电压波到达后级的位置时对后级进行触发，电压波在两级之间水传输线上传播的电长度决定了触发时序。在四级FLTD中，每级的高度为252 mm，理想触发时延约为7.5 ns。正常IVA触发时序下，FLTD各级输出电压V随时间t的变化关系如图 7所示。由于正常触发时磁芯漏电流远小于主电流，因此，由图7可见，本文中模型的计算结果与其他模型的仿真结果相近，电压波形整体趋势与实验也比较吻合。

3.2 支路自放电时各级电压波形

四级FLTD的第二级自放电时电流通路如图8所示。FLTD自放电时，由于相邻各级的主电流通路没有形成，因此电流回路和电压耦合特性与正常放电时存在很大差异。以图 8所示的第二级自放电为例，自放电所在级的磁芯励磁电流方向与正常放电时无异(双箭头所示回路)，而在其他级开关保持断开状态，导致电流只能沿回流板和模块外侧回流立柱流通，无法沿各级电容直接驱动负载，对磁芯产生与正常放电相反的励磁电流(单箭头所示回路)。因此，磁芯所处的励磁状态将对波形产生较大的影响。

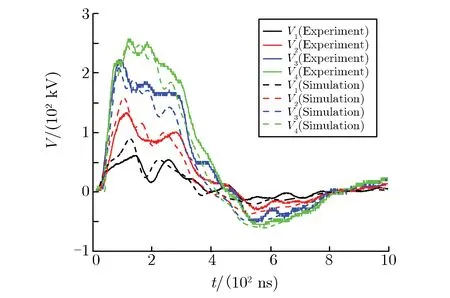
图7 正常IVA触发时序下，FLTD各级输出电压随时间的变化关系Fig.7 V vs. t for FLTD each stage when triggered with IVA sequential

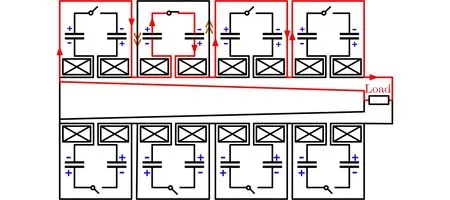
图8 四级FLTD的第二级自放电时电流通路Fig.8 Current path of the second stage self discharge of the four stages FLTD module

当磁芯完全去磁时，即剩磁位于-Br，此时自放电所在级的磁芯励磁过程与正常放电相似，其余各级的磁芯则继续被反向磁化，迅速进入深度饱和状态。由于非自放级的磁芯深度饱和，电极间产生的感应电压几乎为0，因此，自放电所产生的电压可沿次级传输线向上下游传播，电压分布较均匀。仿真中设置第二级单支路自放电，起始剩磁为-1.38 T，放电持续1 μs之后第二级磁芯剩磁为0.5 T，伏秒数消耗约为26 mV·s，其余各级则迅速进入反向的深度饱和状态，最终依然回到-1.38 T的剩磁点附近。

当磁芯未完全退磁时，即剩磁位于-Br～Br之间的某一状态，此时自放电所在级的磁芯被正向磁化直至饱和，其余各级被反向磁化，即不断退磁。由于非自放电级的磁芯并未饱和，因此，在电极间产生了较大的感应电压，对自放电电压快速削弱，使次级传输线上除了自放电相邻级能监测到电压之外，其余各级电压都非常低。仿真中，设置第二级单支路自放电，起始剩磁为0.25 T，放电持续1 μs之后，第二级磁芯进入饱和状态。

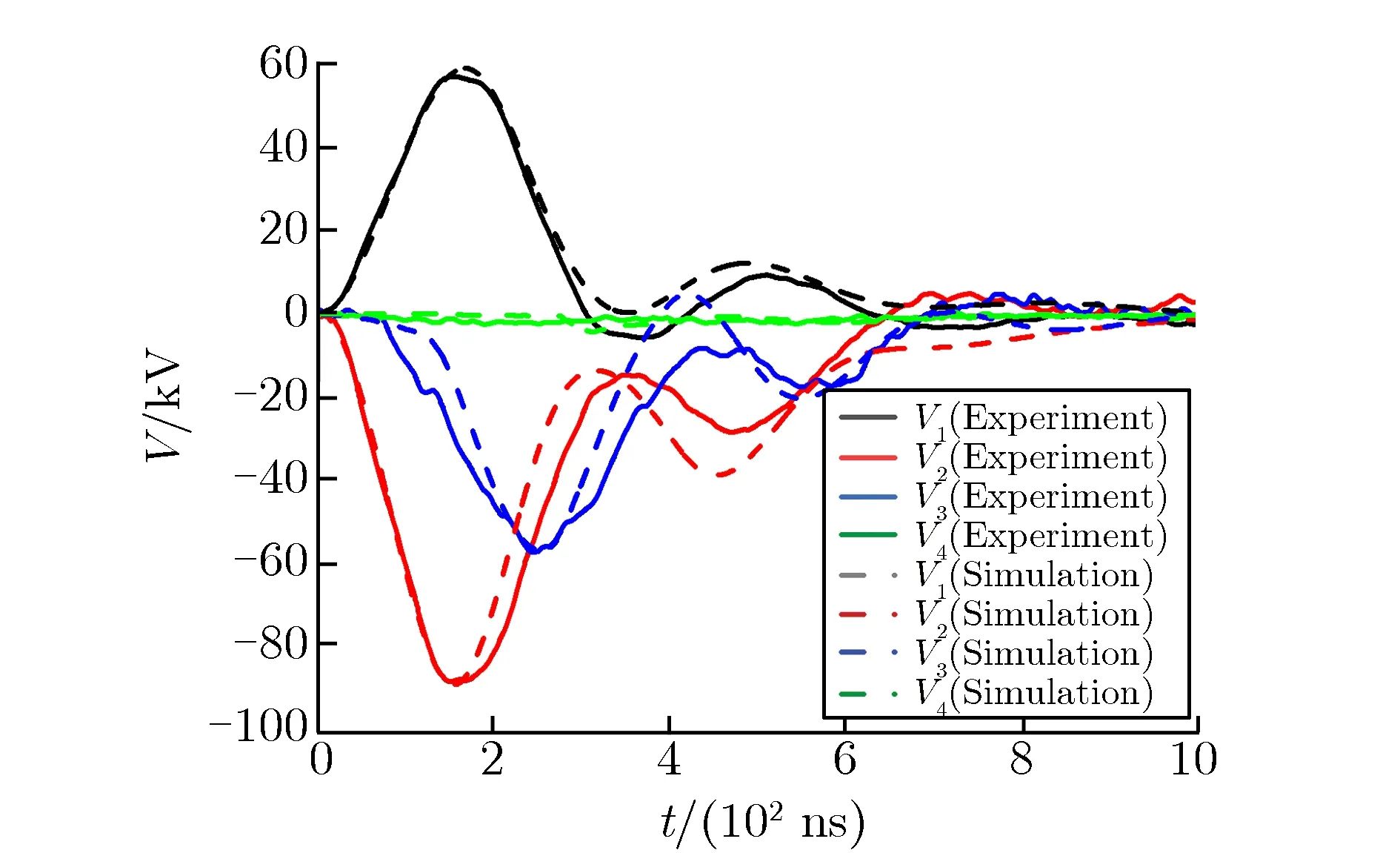
实验中检测到完全去磁后的各级自放电波形如图9所示，采用单向磁化曲线的第二级自放电波形如图10所示。

(a) First stage

(b) Second stage

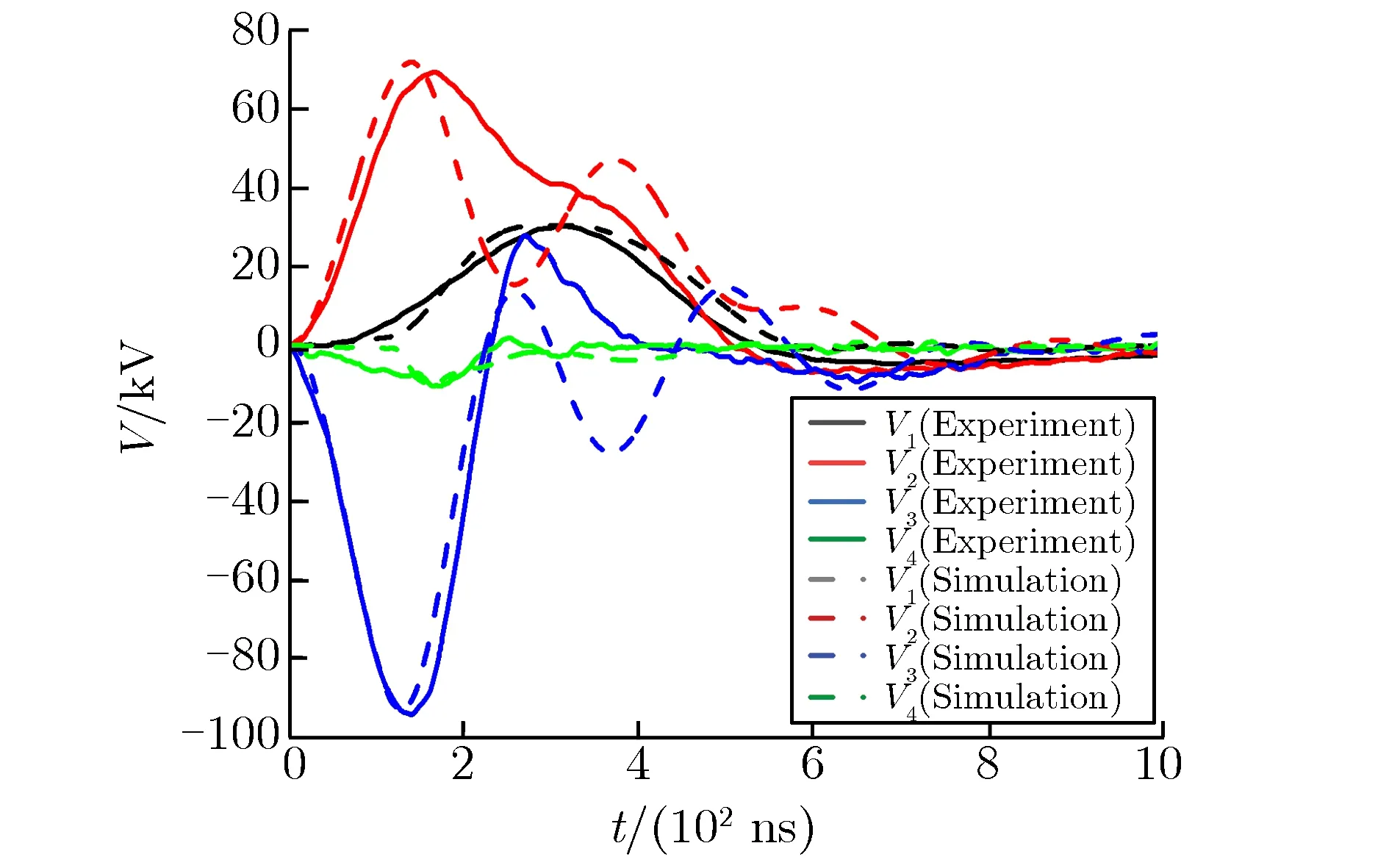
(c) Third stage

(d) Fourth stage

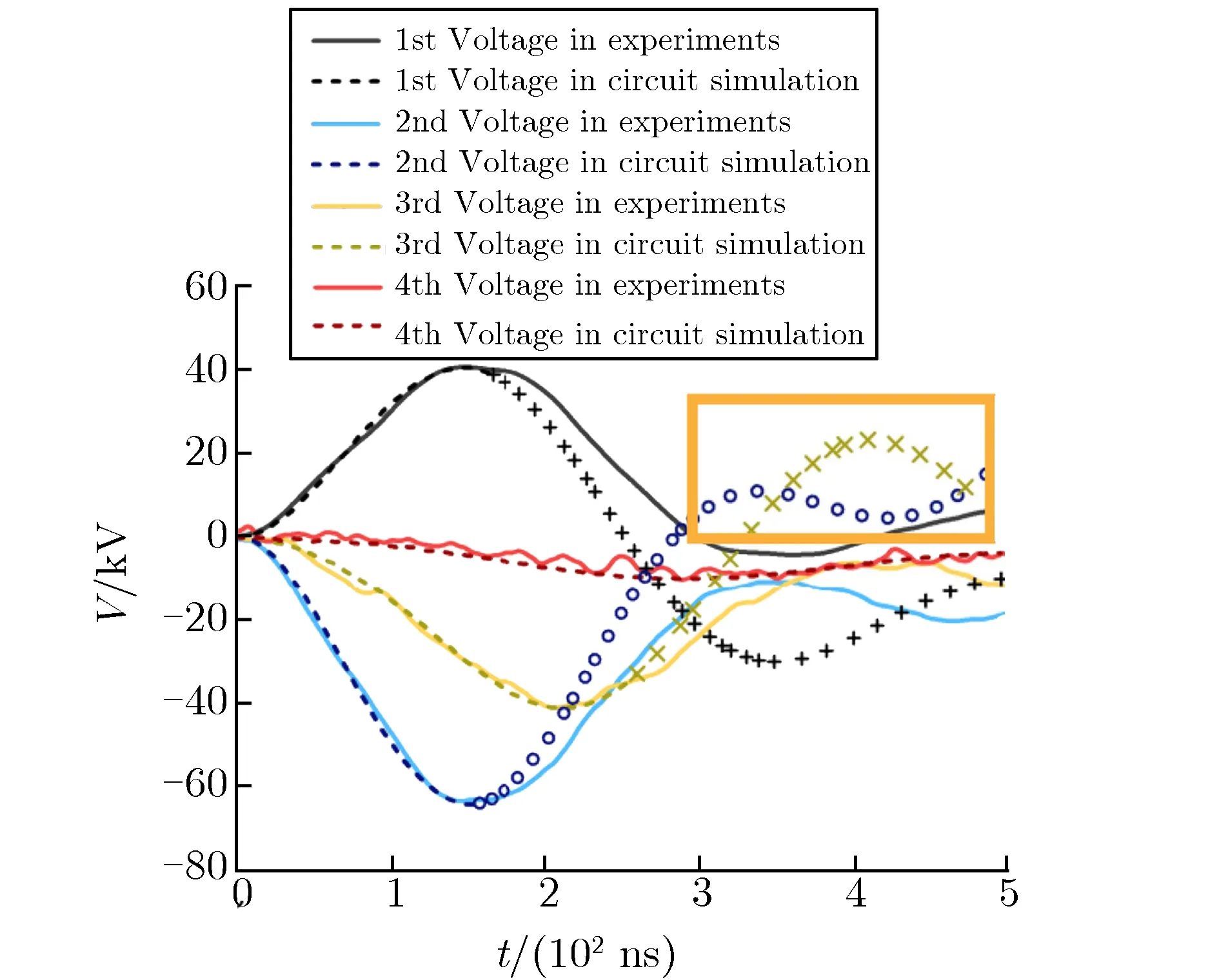
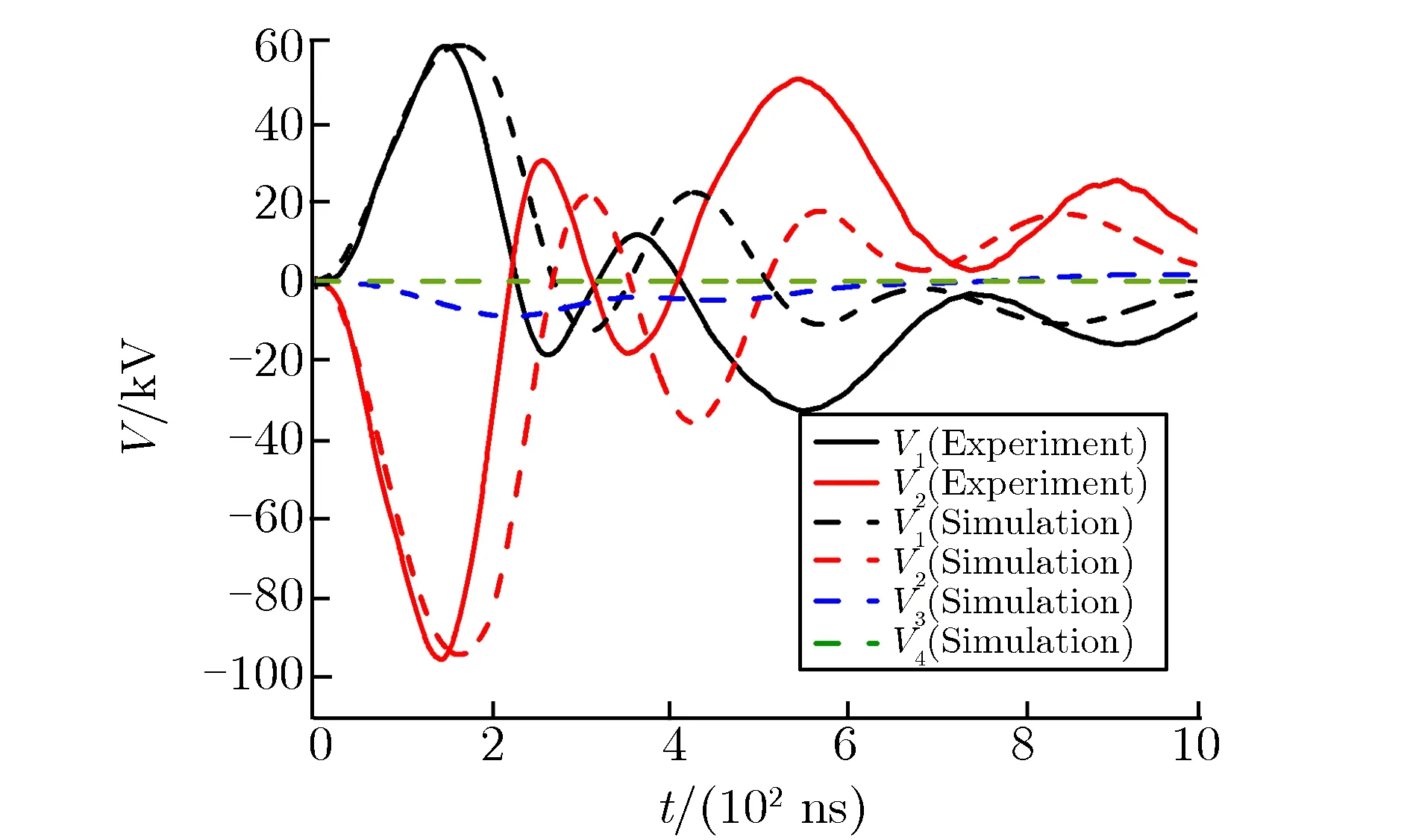
图10 采用单向磁化曲线的第二级自放电波形Fig.10 Simulation waveforms of self discharge on the second stage by using undirectional magnetization curve

由图9可见，模拟结果中第一、二级自放电的波形与实验测得的波形吻合度较高，第三、四级自放电的波形虽没有完全与实验相符，但是与图 10所示的仅考虑单向磁化曲线的磁芯模型仿真结果相比[21]，没有出现因磁芯模型不具备回线特征而导致很大的电压反峰现象。

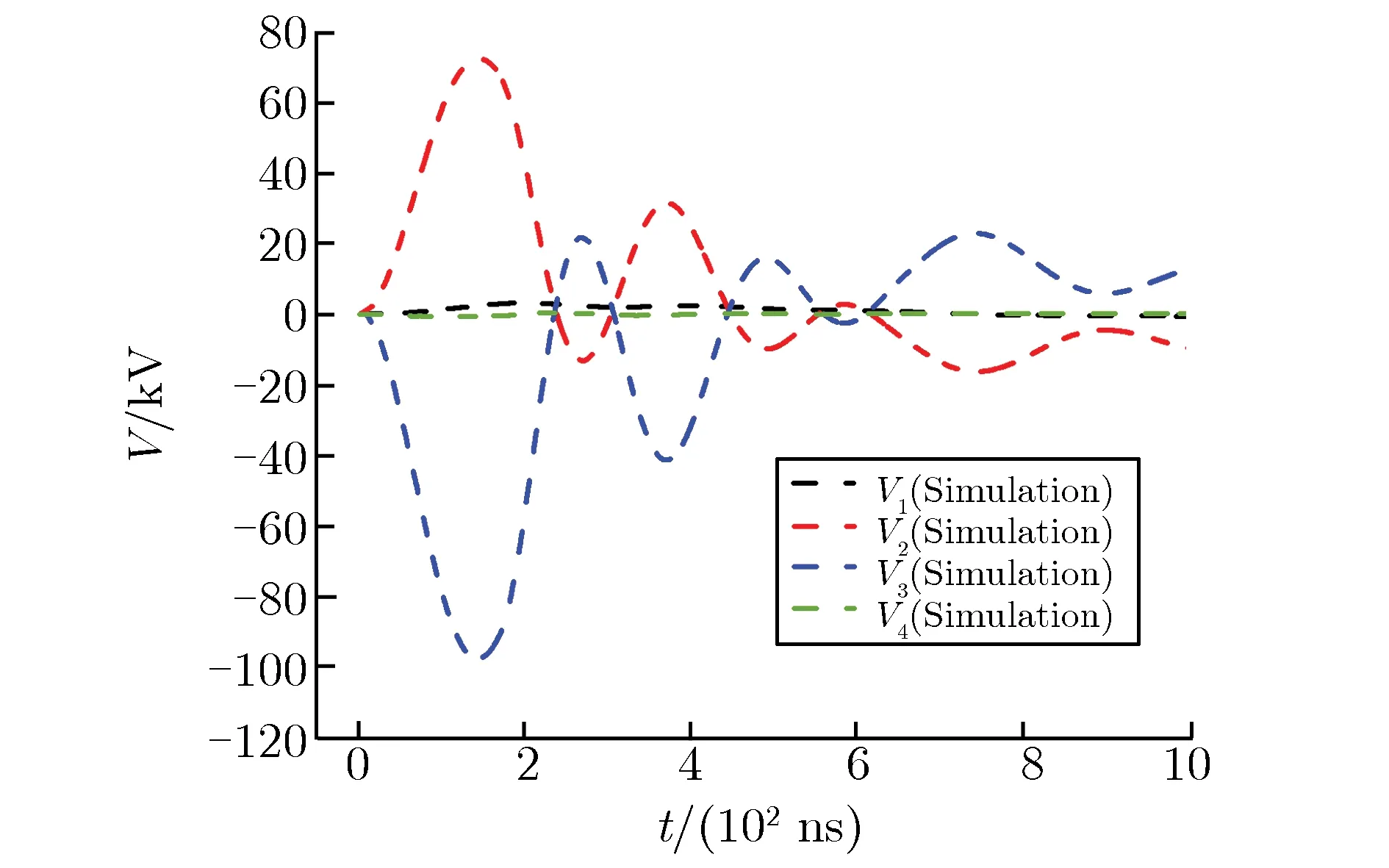
未去磁时，各级自放电电压波形如图11所示。目前已进行的实验中，尚未发生未去磁的是第三和第四级自放电，因此这两级的自放电波形仅为仿真结果。由图11可见，第一和第二级自放电时的仿真波形与实验测得的波形基本一致。

(a) Prefire on the first stage

(b) Prefire on the second stage

(c) Prefire on the third stage

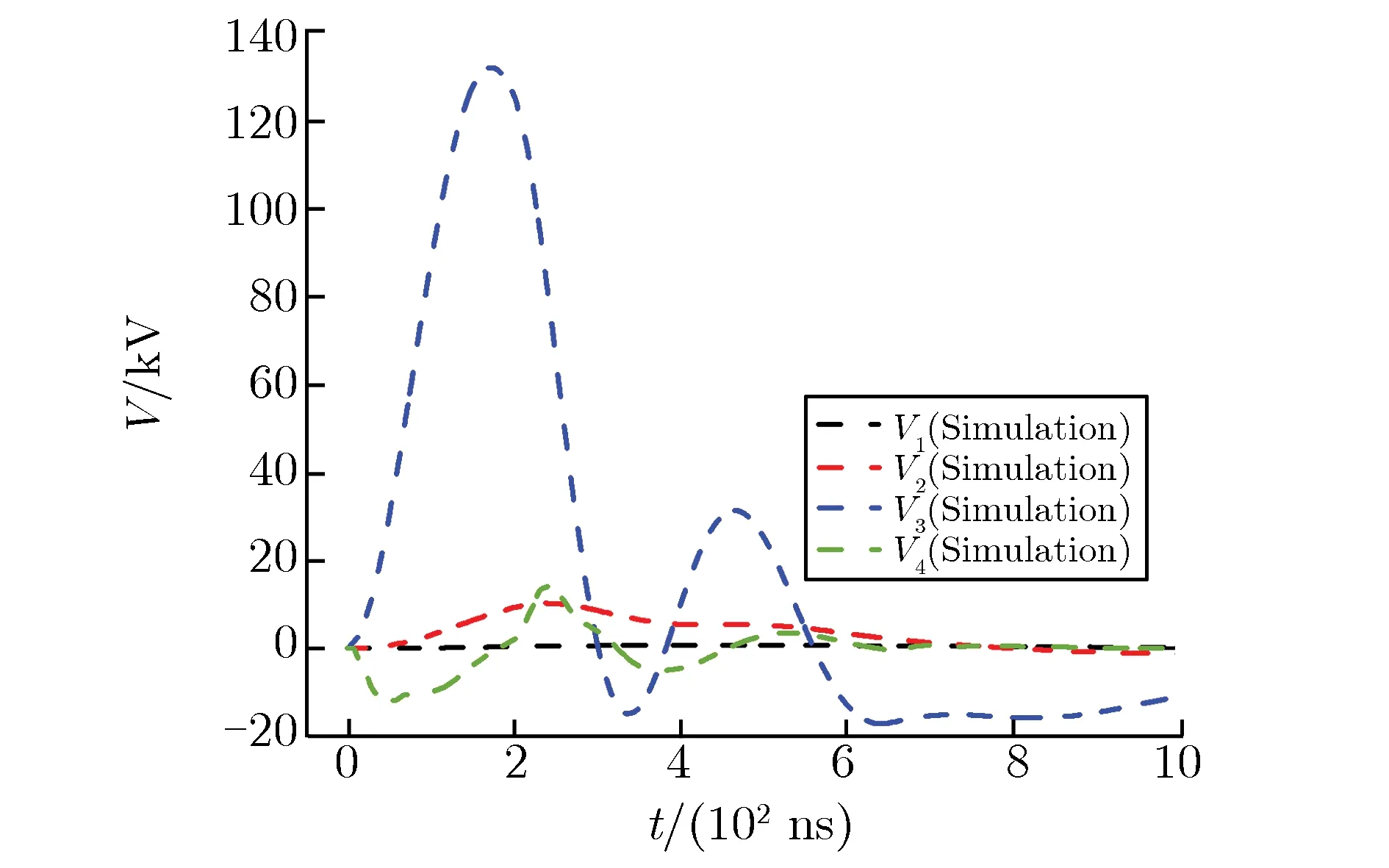
(d) Prefire on the fourth stage

4 结论

本文结合J-A磁滞模型建立了四级FLTD电路模型，对比了模型在正常触发放电、去磁后的支路自放电及未去磁时的支路自放电计算所得的各级电压波形与实验波形的差异。结果表明：在正常触发放电时，模型的计算结果与以往的仿真研究相似，与实验测得的波形趋势吻合；在自放电工况下，与不考虑磁芯非线性特性或仅考虑单向磁化曲线的模型相比，本文模型计算结果更接近于实验波形，在预测和分析自放电故障对FLTD装置的影响时更为准确。在波形的细节上，模拟计算结果与实验仍存在一定差异，需获取更多的实验波形来进一步调整和优化模型参数。仿真计算了不同剩磁条件下发生自放电时，各级磁芯励磁状态的变化规律和水线上各级电压的分布规律，研究表明，去磁后第一次发生自放电是可接受的，而未经去磁时的自放电则会导致自放电所在级的磁芯完全饱和。