单级、双级及四级FLTD电磁及应力分布特性研究

李贞昕，张嘉辉，邱 浩，王曙鸿

( 西安交通大学 电力设备电气绝缘国家重点实验室;西安交通大学 陕西省智能电网重点实验室: 西安 710049)

脉冲功率技术最初是将传输线与发生器结合起来产生高功率纳秒级脉冲,使脉冲功率技术成为一门独立的学科得到发展[1]。快发生器对开关和电容器等器件的要求相当苛刻，用于建造脉冲上升时间为百纳秒内的大型装置在技术上较难实现，且发生器后级电压很高，需变压器油绝缘。与快Marx技术相比，快脉冲直线型变压器驱动源(fast linear transformer driver, FLTD)是近十几年来获得广泛关注的一种新型脉冲功率源技术，可直接产生百纳秒前沿、兆安量级幅值的高功率脉冲电流[2]。1997年，俄罗斯强电流电子研究所Koval Chuk等[3]提出了FLTD的概念和结构，通过电路仿真和实验验证了其设计。2015～2017 年，美国圣地亚国家实验室的学者们[4-6]设计了基于FLTD理论的Z-300及Z-800 等装置，并获取了该装置的全电路等效模型。2016年，西安交通大学张培峰等[7]通过二阶等效电路和粒子仿真分析了10 级串联 FLTD 次级磁绝缘传输线(magnetically insulated transmission line, MITL)的结构和尺寸。FLTD技术上的主要优势是具有较强的容错能力、输出波形调节能力和重复频率运行能力，运行速度快且不用变压器油，开关工作气体为压缩空气，运行维护比较方便[8]，在Z箍缩、X射线闪光照相和高能量密度物理等国防和工业领域具有重要的应用前景，是下一代脉冲功率驱动源最有前景的技术路线[9]。目前，美国圣地亚国家实验室、俄罗斯强电流电子研究所、中国工程物理研究院和西北核技术研究所等科研机构已开展FLTD技术研究及装置研制[1-2]。

目前，国内外对脉冲功率装置多物理场耦合研究中，有限元法(finite element method, FEM)是运用最为广泛的数值计算方法[10-13]。然而，对Z箍缩装置，尤其是FLTD的多物理场耦合分析很少[14]。在FLTD的设计和研发过程中，运用数值计算技术，准确分析电磁性能与机械性能是十分必要的。文献[15-16]利用时域有限积分理论首次研究了4级串联共用、独立腔体结构兆安量级的FLTD在支路放电时的电磁场分布规律。文献[17]使用基于共形网格和并行计算的时域有限积分技术，可降低仿真无线传播和衰减问题的内存消耗和计算时间。为设计高功率微波设备，文献[18]采用场路耦合方法将非线性的电路元件和经过有限积分理论(finite integration theory, FIT)空间离散的场模型耦合至系统方程并求解。文献[19-22]利用基于有限积分理论的CST Studio Suite软件，分别针对静电放电发生器、考虑频变参数的接地网、电力变压器和单级FLTD进行仿真分析，并验证了数值模型的准确性。FLTD脉冲放电过程中，快前沿、高幅值的脉冲电流可激发出瞬变电磁场，同时，电磁力可能导致部分部件发生形变，为FLTD正常工作带来巨大隐患。然而目前的研究中，针对FLTD电磁应力的研究较少，本文通过研究单级、双级与四级FLTD装置全模型及单支路模型的电磁场与体力密度，计算其范式应力与形变。

1 理论模型

在通常的情况下，电磁力的计算包括作用于物体上的体积力和边界上电磁场跃变导致的物体表面力，而体积力和表面力是由一个包含电磁项的一般应力张量推导出来的。因此，对于不同类型的材料，计算电磁力所用的方法和表达式是不同的。

在结构力学模块中，对于线弹性材料，连续介质固体中的柯西方程为

(1)

其中：ρ为材料密度；r为材料中某点的空间坐标；T为应力张量；fext为外部体积力。

对于应力张量T，可分解为基于电磁场和基于应力场的2部分，表示为

T=TEM+σM

(2)

其中：TEM为电磁场导致的应力张量；σM=DεE为弹性导致的应力张量；D为弹性矩阵；εE是弹性应变分量。

通常用体积力而非应力张量来表示电磁力，表示为

(3)

其中，fEM为电磁场中的电磁力。

因此，当系统加速度为0时，静态力平衡方程可表示为

(4)

对于载流导体，使用洛伦兹力公式计算电磁力，表示为

fEM=J×B

(5)

其中：J为电流密度，B为磁通密度。

则力平衡方程可表示为

(6)

对于磁性材料，使用麦克斯韦应力张量法计算电磁力，表示为

(7)

其中：H为磁场强度；n为法线方向单位矢量

对于非磁性的电介质材料，则使用虚功法计算电磁力。

将计算得到的电磁力分布数据导入结构场中，根据应力应变的弹性本构关系，获得模型中各部件的应变量。

2 电磁场计算

2.1 一级与多级放电回路

在单级、双级与四级FLTD模型的电磁仿真中，认为同一级FLTD中的所有放电支路开关是在同一时刻触发导通的，忽略开关自导通开关触发时间的差异及开关导通的抖动时间。单级FLTD由23个放电支路并联组成，双级及四级FLTD模型分别由2层和4层单级模型叠加而成，各级之间为串联关系。FLTD单个放电支路的仿真模型、单级模型及四级模型如图1所示。

(b) Planar graph of the single stage FLTD device

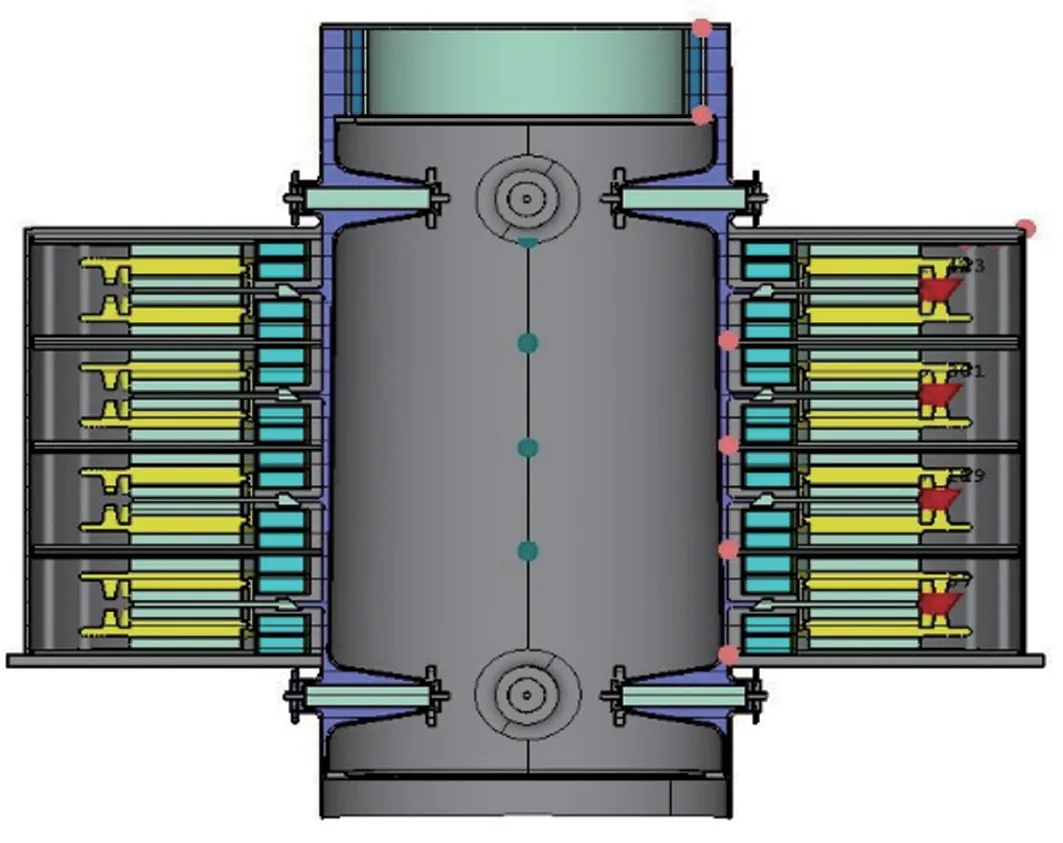
(c) Sectional view of four stages FLTD simulation model

FLTD的激励源为每个放电支路中的两个串联电容，单个放电支路的等效电容为50 nF、初始充电电压为200 kV(±100 kV)，零时刻开关导通后，电容放电产生脉冲电流。四级FLTD电路如图2所示。

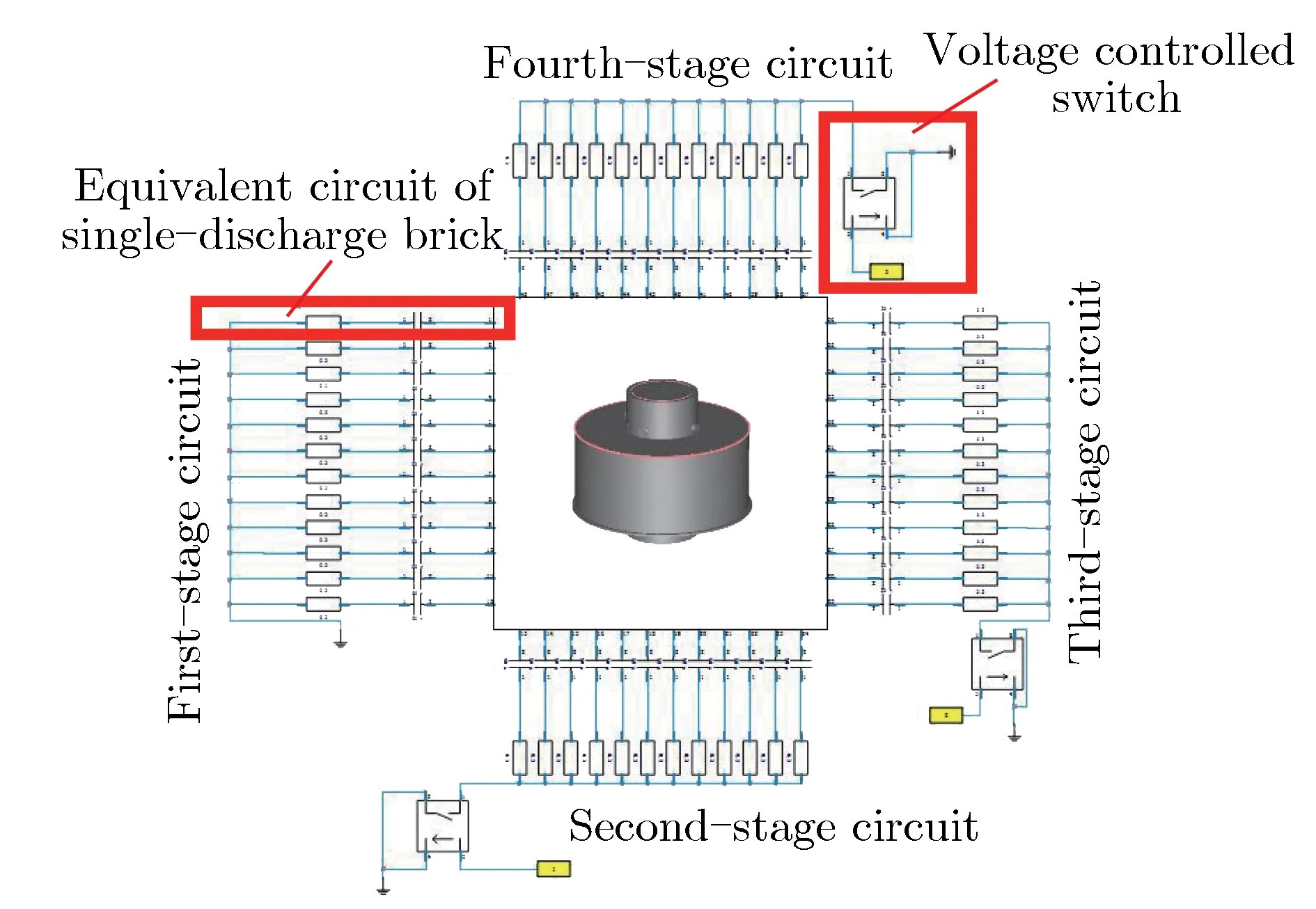
图2 四级FLTD电路图Fig.2 Diagram of four stages FLTD circuit

图2中，居中位置为四级带负载FLTD装置，四周分别为一至四级等效电路。该装置为对称结构，需设置对称边界条件，仅对一半放电支路加载等效电路，可缩短计算时间，提高计算效率。一至四级电路中，每级各包含12个放电支路。0时刻，一级电路放电并产生脉冲电流，经过一个时延后，二级电路放电，以此类推，每级电路的放电时间均较前一级电路滞后一个放电时延，该时延及开关导通时间由各级压控开关控制。四级FLTD装置各级输出电流波形如图3所示。由图3可见，一级电流值从零时刻开始以脉冲形式快速增加，各单支路放电完成，电流到达峰值后，该级电流开始快速衰减；二级至四级电流均符合该放电规律，且各级的触发时间依次顺延。由于各级装置之间是串联连接，因此，各级电流理论上相同，只是在触发时间上存在延迟，但由于装置工作过程中腔体结构中的电感与寄生电容在高频下发生谐振，导致电流波形出现不同程度的抖动。

图3 四级FLTD装置各级输出电流波形Fig.3 Output current curves of four-stage FLTD

各级单支路的放电电流波形中，一级FLTD单支路的第一个输出峰值电流Ip1=37 165.449 A，在112.7 ns出现，第二个电流峰值Ip2= 4 115.637 7 A在621.43 ns出现，电容C=50 nF；二级模型单支路的第一个峰值电流Ip1=34 244.418 A在115.17 ns出现，第二个电流峰值Ip2=3 648.336 2 A在618.25 ns出现；四级模型单支路的第一个峰值电流Ip1=34 088.484 A在147.43 ns出现，第二个电流峰值Ip2=5 516.42 A在583.36 ns出现。每一级的单支路放电电容之间为并联连接，因此，同一级的电容放电值为同级所有电容放电量之和，本文研究的FLTD装置为单级23支路模型，单级全支路输出的总电流峰值约为该级单支路峰值的23倍。各级单支路之间属于串联连接，理论上各级电流值相同，但由于各级支路存在振荡放电过程及腔体电感与寄生电容谐振等现象，造成了能量损失，使各级的电流峰值存在差异。四级FLTD全支路输出总电流波形如图4所示。

图4 四级FLTD全支路输出总电流波形Fig.4 Total output current curve of four stages FLTD

2.2 电磁场计算

本文所研究的FLTD装置为对称结构，为节约计算机空间、加快计算速度，在计算应力时，使用一至四级的单支路带负载FLTD模型，仍可保证数值模型的简化不影响计算结果。在FLTD装置全模型中，模拟装置的真实工况为各个单放电支路加载RLC电路，计算各级单支路的电流和电压。将四组电流分别加载到一至四级的单支路仿真模型中，并计算电磁场及电磁应力。一级、二级与四级FLTD单支路电磁仿真模型如图5所示。

(a) Single stage

(b) Two stages

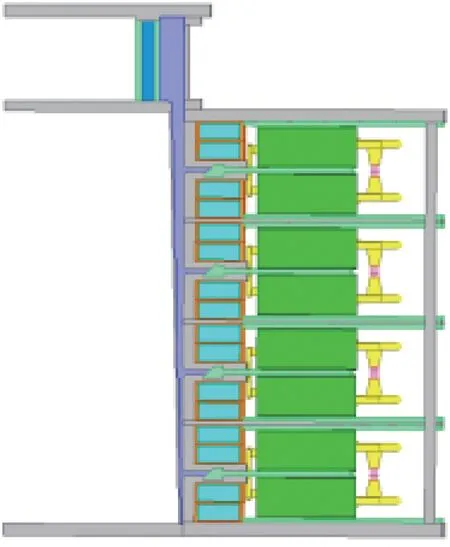
(c) Four stages

一级模型单支路的第一次电流峰值出现在112 ns。为进一步了解各支路的放电过程及电流流通路径，计算了装置一个工作周期内的电流密度。10，112，600 ns处的电流密度J可分别代表装置在放电初期、放电峰值期及放电末期的状态。不同时刻，一级FLTD单支路模型电流密度分布如图6所示。

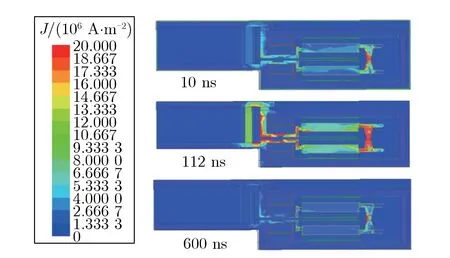
图6 不同时刻，一级FLTD单支路模型电流密度分布Fig.6 Current density distribution of single stage single brick FLTD model

由图6可见：由电容产生的电流流经负载形成回路，电流密度分布较集中区域为电容的放电端；在运行初期，电流密度分布主要集中在电容的放电端，随着电流幅值增加，电流密度开始向负载端移动，可认为能量最终流向了负载；电流峰值降低后，电流密度峰值回到电容放电端，负载内的电流密度开始降低。

二级模型单支路的第一次电流峰值出现在115 ns左右，将一级与二级电流加载到二级FLTD单支路模型中，计算电流密度分布。不同时刻，二级FLTD单支路模型电流密度分布如图7所示。

图7 二级FLTD单支路模型电流密度分布Fig.7 Current density distribution of two stages single brick FLTD model

由图7可见：二级FLTD带载模型在运行前期，第一级与第二级支路中的电流放电端先后开始放电，电流开始逐步流向负载，在115 ns附近，负载内电流密度达到最大；随着电流幅值降低，两级放电端的电流密度均开始下降，第一级的电流密度在时间上先于第二级衰减至0；600 ns时，一级放电电容端口处电流密度明显小于第二级端口，此时，负载内的电流密度平均值也衰减至峰值的1/8以下。

四级模型单支路的第一次电流峰值出现在147 ns，将一至四级电流加载到四级FLTD单支路模型中，计算一级支路放电至四级支路放电完成一个工作周期内的电流密度分布。不同时刻，四级FLTD单支路模型电流密度分布如图8所示。

由图8可见：在四级FLTD单支路带载模型运行前期，一至四级支路中的电流放电端依次开始放电，电流开始逐步流向负载，在147 ns附近，负载内电流密度达到最大；随着电流幅值降低，四级放电端的电流密度均开始下降；600 ns，电容放电端口处的电流密度基本衰减至0，整个系统中只剩下腔体壁上的残余电流密度，负载中的电流密度衰减为0。

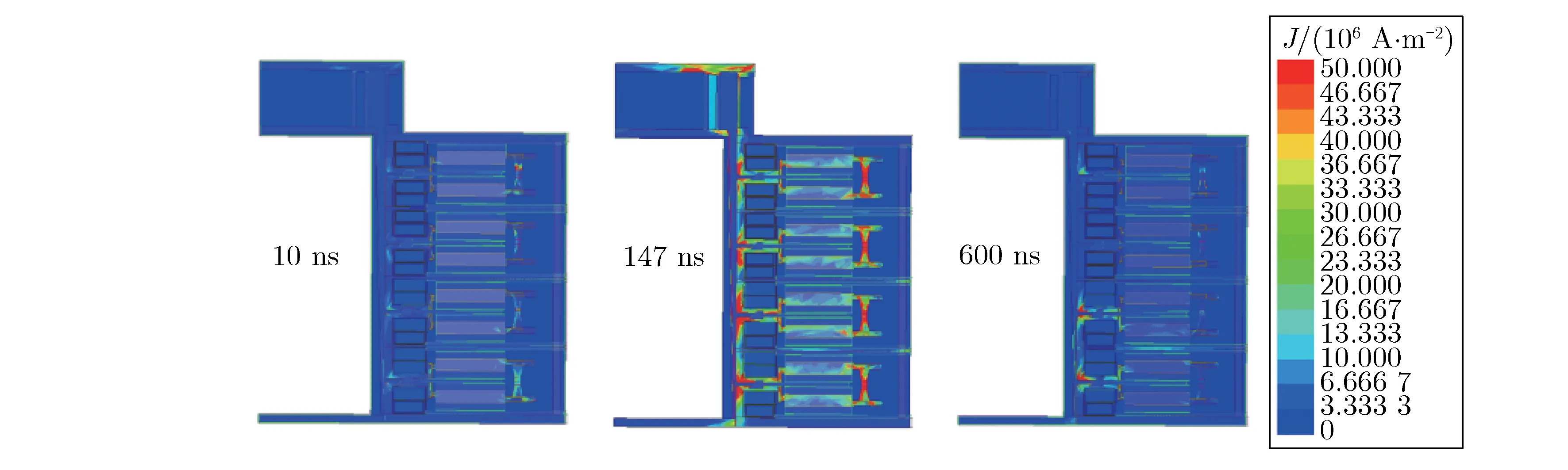
图8 不同时刻，四级FLTD单支路模型电流密度分布Fig.8 Current density distribution of four stages single brick FLTD model

3 结构场计算

FLTD装置的工作过程中，电磁场剧烈变化，直接产生百纳秒前沿、兆安量级幅值的高功率脉冲电流，对装置的机械强度带来巨大挑战。因此，需研究装置的电磁应力与总形变量，寻找装置应力集中点，验证装置结构的可靠性。

计算FLTD一至四级模型的电磁场及电磁应力后，将电磁体积力密度导入结构场中，计算结构应力。在计算结构场时不考虑液体应力，因此，将模型中的假负载和内外筒之间的去离子水删除。为模拟FLTD装置真实工况，考虑各个部件之间的相互作用关系，设置所有的固体结构共节点；四级FLTD装置工作时，直立放置并固定于地面，因此，在模型底面施加固定支承，防止装置受振动后移位；并考虑装置自身重量，为模型加载标准地球重力。在计算时，首先模拟装置自身稳定过程，即装置受地球重力影响由开始受力至达到平衡状态，待装置稳定后，再加载各级模型的体积力密度。选择合适的网格尺寸和网格形状对仿真模型进行网格剖分，一级、二级及四级FLTD应力模型的网格剖分如图9所示。

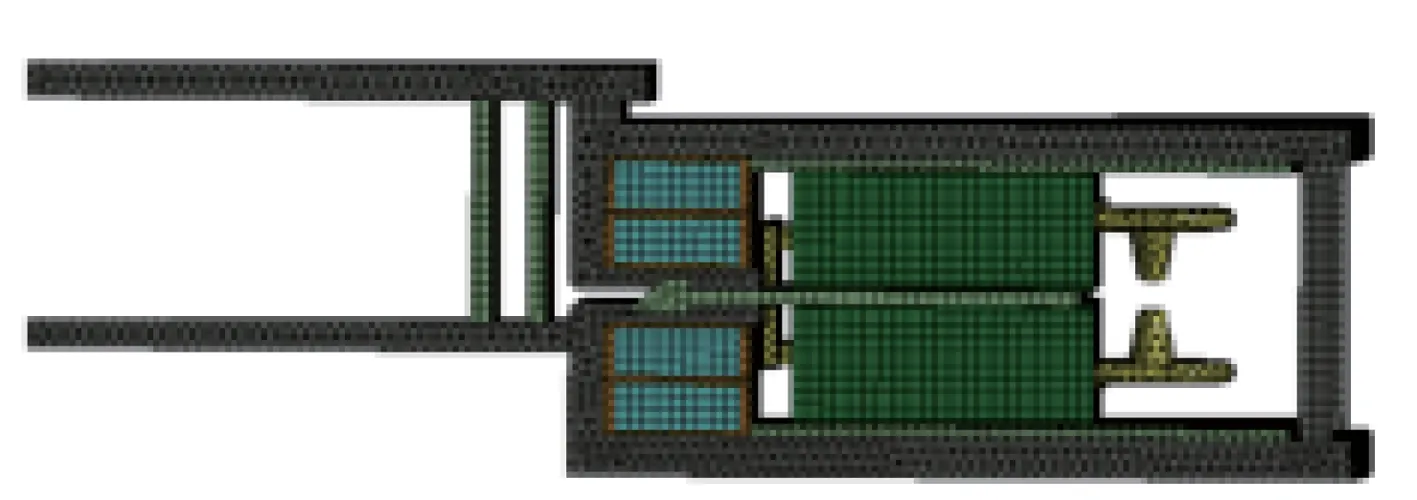
(a) Single stage

(b) Two stages

(c) Four stages

3.1 一级FLTD单支路模型

计算一级FLTD单支路模型的范式应力F与总形变x。一级FLTD单支路模型应力分布如图10所示。由图10可见，一级FLTD单支路模型的应力峰值出现在支撑柱顶端，为3.05×107Pa，范式应力远小于材料的限值，不会导致塑性形变的发生。由于不同材料的应力承受能力不同，因此，还需进一步研究模型的总形变。一级FLTD单支路模型总形变分布如图11所示。

图10 一级FLTD单支路模型应力分布Fig.10 Stress envelope distribution of single stage single brick FLTD model

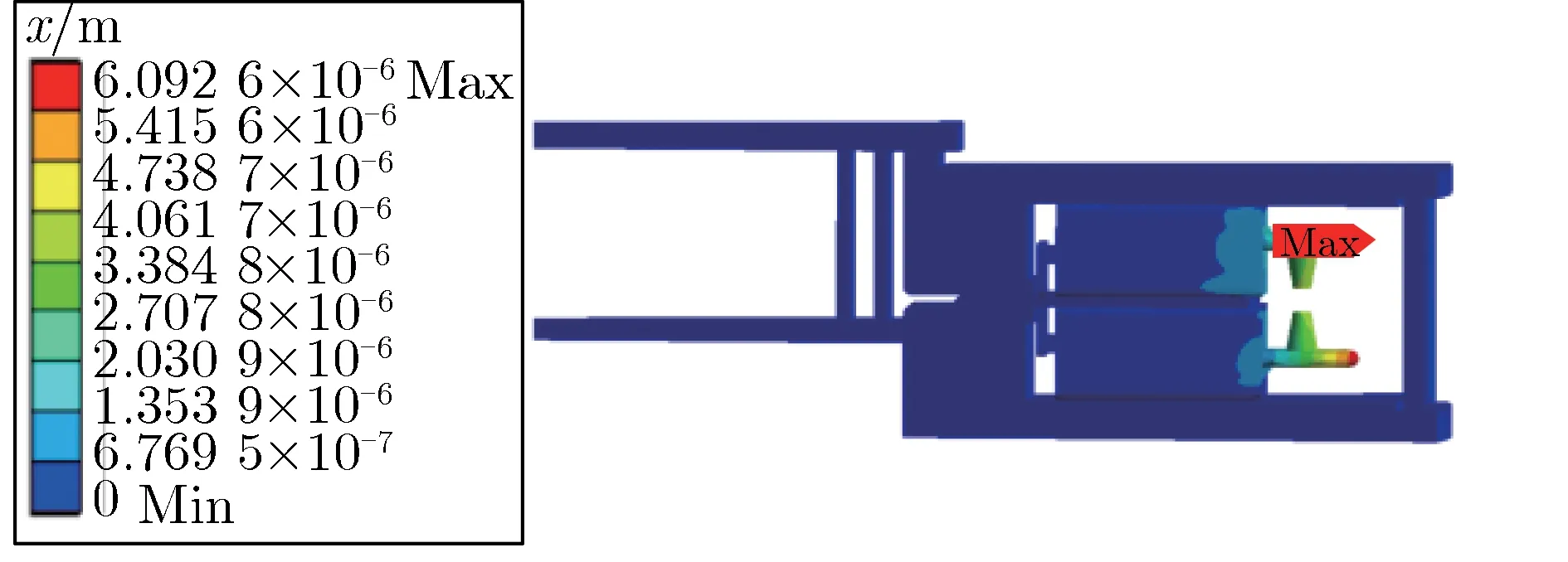
图11 一级FLTD单支路模型总形变分布Fig.11 Total deformation distribution of single stage single brick FLTD model

由图11可见，最大形变出现在铝制放电端口，为6.09 μm，且为弹性形变，对于几何模型的影响较小。结合图10与图11可见，一级FLTD模型的最大形变出现在铝质的电容放电输出端口处，而应力峰值出现在钢制回流柱上。这是因为钢的机械强度强于铝，因此，最大形变没有出现在回流柱上。

3.2 二级FLTD单支路模型

二级FLTD单支路模型在工作过程中，放电端的数量为一级模型的2倍，该模型承受的应力冲击是由双脉冲放电引起的。因此，有必要对二级模型的应力与形变进行计算。二级FLTD单支路模型应力分布如图12所示。

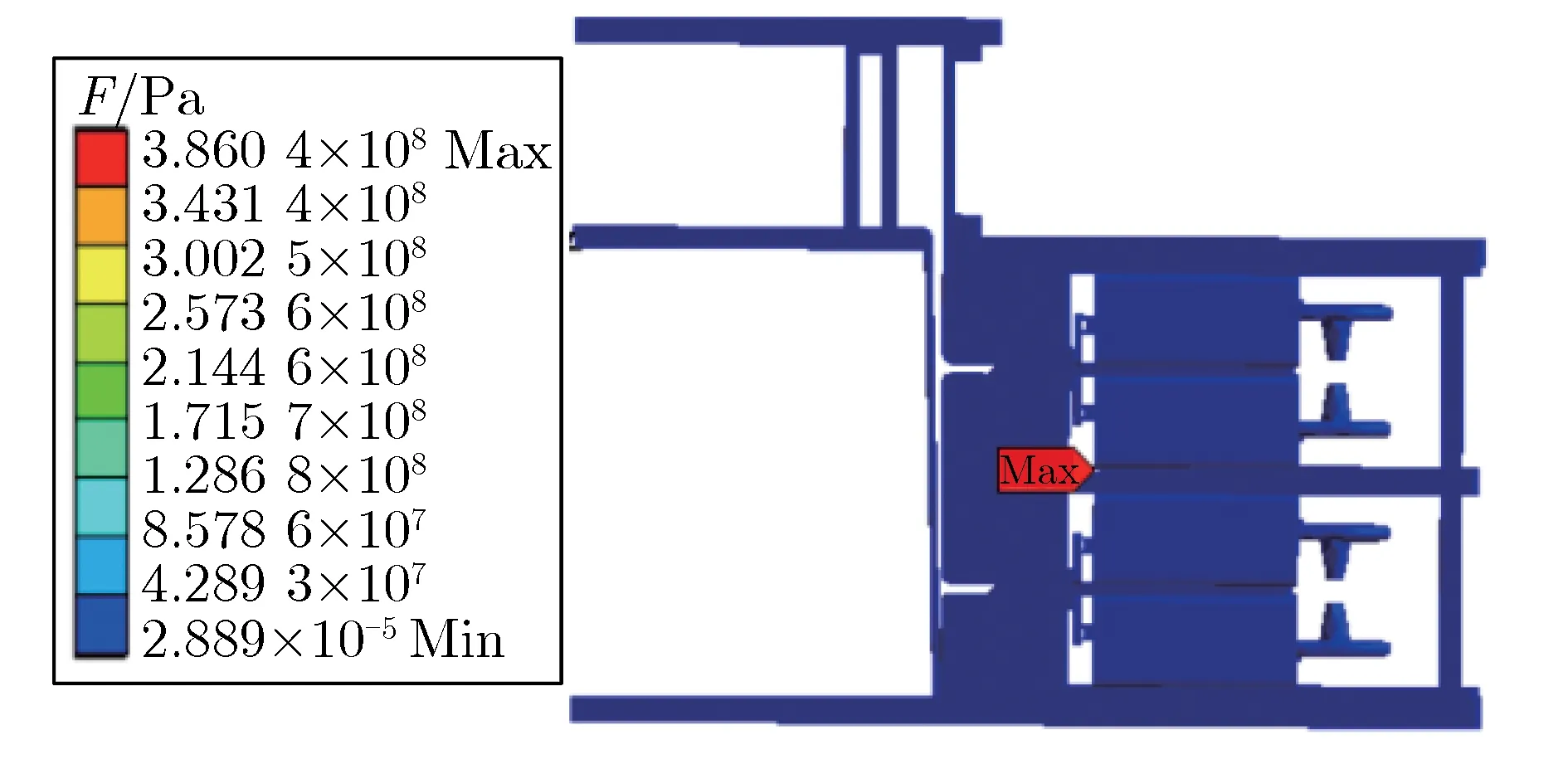
图12 二级FLTD单支路模型应力分布Fig.12 Stress envelope distribution of two stages single brick FLTD model

由图12可见，二级FLTD单支路模型的应力峰值为3.8×108Pa，远小于材料的限值。二级FLTD单支路模型总形变分布如图13所示。

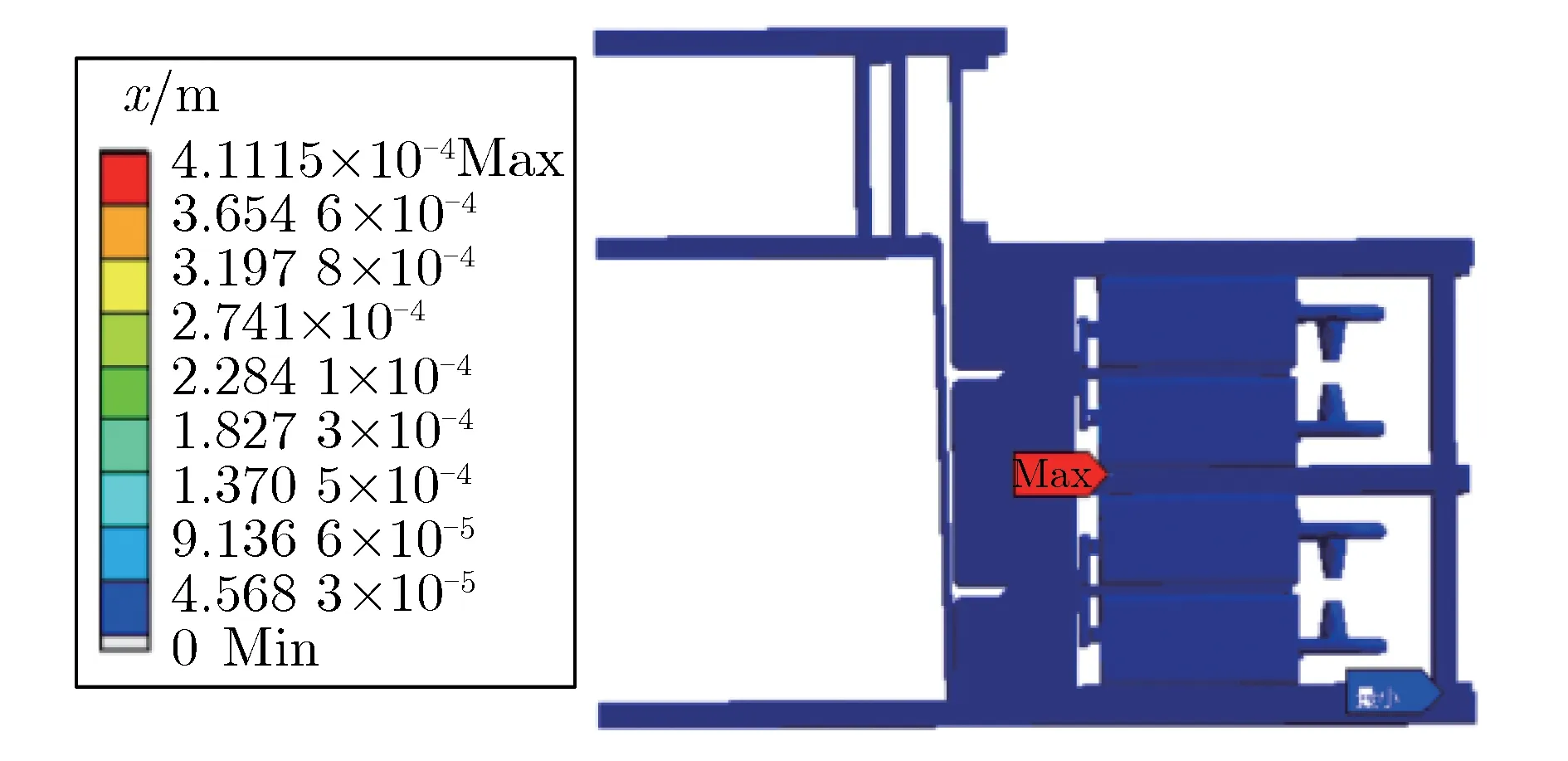
图13 二级FLTD单支路模型总形变分布Fig.13 Total deformation distribution of two stages single brick FLTD model

由图13可见，二级单支路FLTD模型中，最大形变量为0.41 mm。经分析，该位置属于两种材料交界处，网格剖分过程中，该位置的网格质量不佳，导致计算出现奇异点，造成该位置的大形变量。解决该问题需对材料交界面上的网格进行加密处理，但这会大大增加计算量，增加计算时间，且对计算机内存要求较高。但由于该奇异值仍在材料承受范围内，因此，不再对网格进行加密处理。

3.3 四级FLTD单支路模型

目前，国内外学者对四级FLTD装置有较高的关注度，本文对四级单支路FLTD模型进行了应力计算。四级FLTD单支路模型应力分布如图14所示。应力存在明显的累积效应，最终的应力值是各个时刻电磁力及重力等矢量的累积值，在装置工作过程中应力释放与累积同时存在。

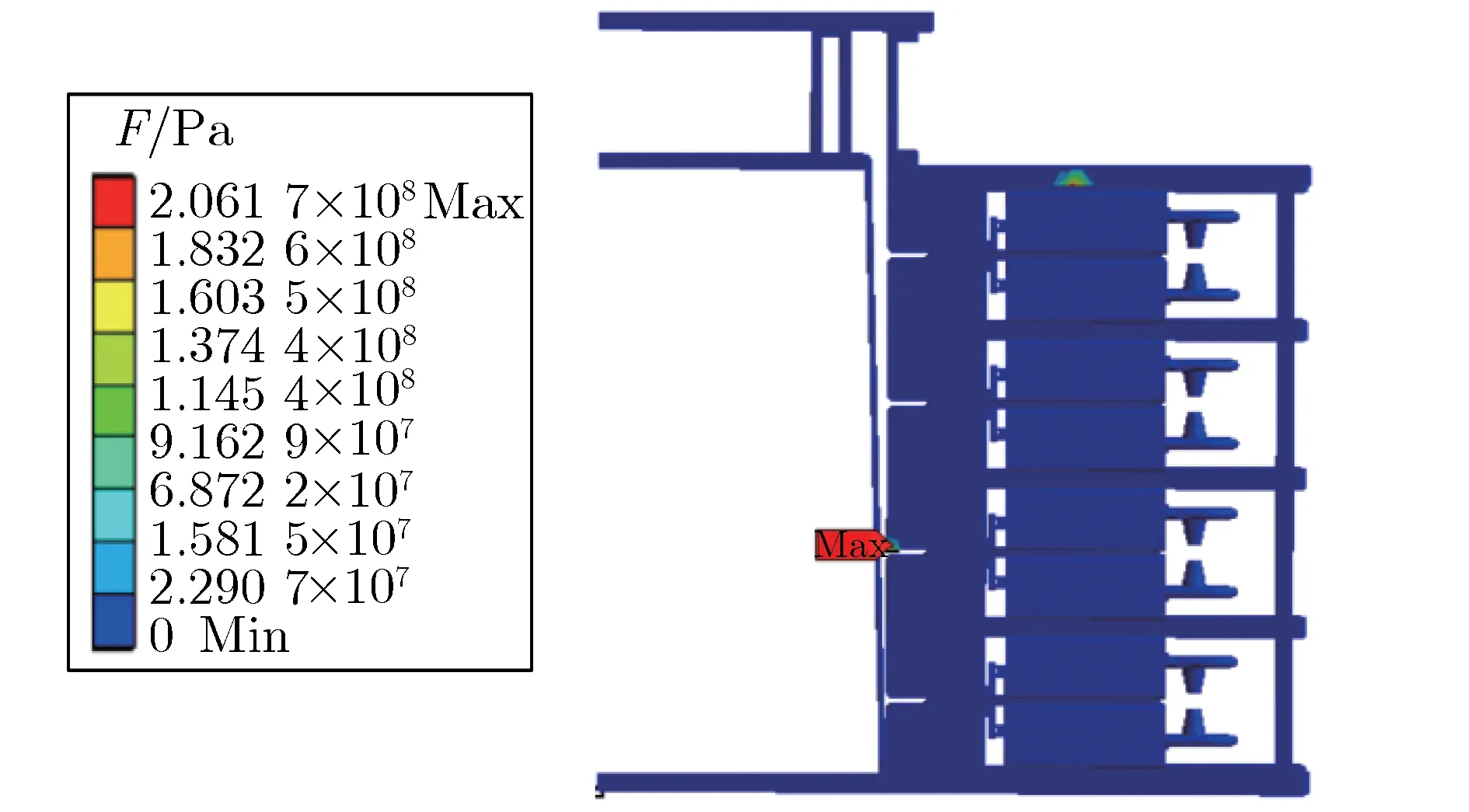
图14 四级FLTD单支路模型应力分布Fig.14 Stress envelope distribution of four stages single brick FLTD model

由图14可见，四级单支路模型的应力峰值为2.06×108Pa，远小于材料的限值。某时刻的应力值仅能反映该时刻该位置所受的应力，但材料本身弹性可抵抗部分应力，因此，在研究形变时，需考虑最终累积的形变量。四级FLTD单支路模型总形变分布如图15所示。

图15 四级FLTD单支路模型总形变分布Fig.15 Total deformation distribution of four stages single brick FLTD model

由图15可见，四级单支路FLTD模型中，最大形变出现在铝制放电端处，最大形变量为0.030 9 mm，对模型结构无影响。该位置与一级最大形变量出现位置相同。

4 结论

本文首先对四级带负载FLTD全模型加载对称边界条件，然后对四级模型的每个放电支路加载等效放电电路，并进行仿真计算，以模拟FLTD的真实工作情况。计算结果表明：四级FLTD单支路输出电流峰值为35 000 A，到达第一次峰值所需时间小于150 ns，各级各支路放电平稳，各级输出的脉冲电流上升时间及峰值均符合预期；四级FLTD全模型输出的总电流峰值为788 090 A，第一次到达峰值时间为188.1 ns，符合FLTD工作的基本要求。

分别建立了一级、二级与四级FLTD单支路仿真模型，将前述计算得到的各级放电电流作为输入，加载到各级放电支路中，并对电磁场及体积力密度进行计算，并将结果耦合到结构力学中，计算范式应力与形变。计算结果表明：一级至四级FLTD单支路带负载模型的最大形变出现在铝质的电容放电输出端处，范式应力峰值为2×108Pa，远小于材料限值。该FLTD模型结构具有良好的机械稳定性。