具有子圆环的圆环金属网栅电磁屏蔽特性

张博文，张怡蕾，陆振刚,3†

(1. 哈尔滨工业大学 超精密光电仪器工程研究所；2. 超精密仪器技术及智能化工业和信息化部重点实验室: 哈尔滨 150006；3. 强脉冲辐射环境模拟与效应国家重点实验室，西安 710024)

近年来，随着不同波段的电磁波在雷达无线通信和便携式电子设备等领域的广泛应用，人们所处的电磁环境日益复杂。无处不在的电磁波会影响人们的健康和仪器设备的可靠性与稳定性[1-4]，尤其是在航空、军事和医疗器械等领域，仪器设备精度极高，更易受到电磁波干扰的影响，导致结果精度不佳甚至设备失效[5-7]，这使电磁屏蔽技术日益引起人们的广泛关注和重视。光学透明器件的电磁屏蔽是其中一项难题，以光窗等透明器件为例，目前所提出的解决方法包含透明导电薄膜[8]、频率选择表面[9-10]及金属网栅[11-12]等。与其他技术相比，金属网栅可实现可见光至红外宽波段良好的透光性及较强的微波波段电磁屏蔽效率。同时，以光刻技术为代表的金属网栅加工工艺已成熟，可进行大批量生产，成为近年来的研究和应用热点之一[12-17]。

金属网栅的图形形态及结构参数将会影响透光性及电磁屏蔽性能，已由最早，也是最经典的方格网栅逐步演变为圆环网栅及6边形网栅等复杂结构[17-19]。网栅周期作为金属网栅最重要的结构参数，直接决定了网栅的电磁屏蔽效率。对结构复杂的金属网栅，往往采用等效周期来代替实际周期进行屏蔽效率的理论计算。因此，在网栅设计过程中，更准确的等效周期可大大提高计算结果的准确性。随着网栅演化愈发复杂，特别是包含有子圆环的金属网栅的出现，亟需高精度的等效周期计算方法。

针对这一问题，本文从考虑金属网栅的图形结构分布特征入手，提出了一种基于面积加权的等效周期计算方法，结合等效薄膜理论计算网栅屏蔽效率，并将计算结果同电磁仿真软件CST Studio Suite(CST)的仿真结果比对，对该方法的准确性进行了验证。最后，考虑了子圆环转角、子圆环数及入射波偏振状态等因素，分析了不同条件下金属圆环网栅电磁屏蔽效率的变化趋势，为金属网栅设计提供一定参考。

1 金属网栅屏蔽效率分析的复数等效折射率模型

电磁屏蔽效率(shielding effectiveness, SE)是金属网栅的重要性能指标，对其进行快速且精确的计算一直是人们追求的目标。1961年，Ulrich[20]提出了等效电路法，将金属网栅等效为二端口网络电路模型下的阻抗参数，进而用电路的方法实现屏蔽效率计算。1993年，Kohin等[21]提出了金属网栅等效薄膜模型(equivalent refractive index model, ERIM)，将金属网栅等效成了一层实数折射率为ne的薄膜，通过分析薄膜透射率的方法来进行SE计算。1989年，Ciddor等[22]提出了一种应用于周期性金属网格的复数ERIM模型(complex equivalent refractive index model, CERIM)，2016年，陆振刚等[23]对该模型进行了改进，改进后的新模型(modified equivalent reactance and resistance model, MERRM)可很好地分析单层及双层结构金属网栅的SE，特别是对高透光情况具有较高的分析精度。本文采用MERRM模型进行网栅屏蔽效率分析，可表示为[23]

ne=n-ik

(1)

(2)

(3)

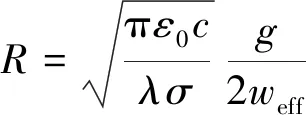
(4)

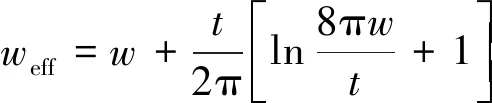
(5)

(6)

(7)

(8)

其中：ne为金属网栅复等效折射率；n为金属网栅等效折射率的实部；k为金属网栅等效折射率的虚部；ZLZL为金属网栅的等效电抗；R为金属网栅的等效电阻；de为金属等效薄膜的厚度；λ为入射电磁波的波长；c为真空中的光速；ε0为真空介电常数；σ为金属直流电导率；weff为金属网栅的等效线宽；g为金属网栅的等效周期；w为金属网栅线宽；t为金属网栅厚度；bM为等效电抗系数；ω为归一化入射频率；ωLZ为网栅归一化共振频率。

假定金属网栅等效为一层厚度为de、折射率为ne的薄膜，衬底的厚度为h，衬底的折射率为ng，空气的折射率为n0，电磁波在单层网栅阵列等效薄膜中的传播如图1所示。

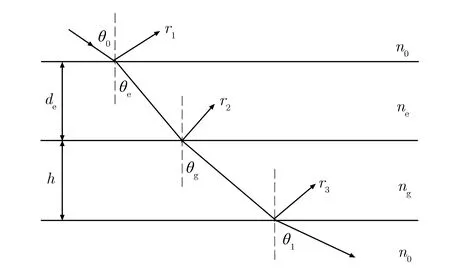
图1 电磁波在单层网栅等效薄膜中的传播示意图Fig.1 Schematic diagram of electromagnetic wave propagation in a single-layer grid equivalent film

以S波为例进行分析，根据菲涅尔公式可求得各分界面处的反射系数，表示为[24]

(9)

由多光束干涉理论可得衬底与空气的总反射系数，表示为

(10)

(11)

同理，整个网栅结构的等效薄膜反射系数表示为

(12)

(13)

在忽略整体结构吸收的情况下，网栅的电磁屏蔽效率表示为

(14)

由式(1)-式(14)可知，金属网栅线宽w固定的情况下，等效折射率ne将由网栅等效周期g决定，而等效折射率ne又决定了整体结构的反射系数r，从而决定了电磁屏蔽效率。由此可知，等效周期g的求取将决定模型计算结果的准确性。

2 多子圆圆环金属网栅等效周期的获取方法

为得到更准确的等效周期，本文提出一种基于面积加权的等效周期计算方法。核心思想是：首先，分别对一个周期内网栅各通光孔图形的子等效周期进行计算；然后，根据各通光孔图形面积在总图形面积中所占的比例，对所有子等效周期进行加权求和；最后，得到整个金属网栅对应的等效周期。

以包含2个相外切子圆环为例，图2为水平及竖直方向切割示意图。首先，将圆环网栅根据独立透光区域划分为几部分，进而在分析每一透光部分水平方向子等效周期时，采用数根水平等间距分布的直线将该部分透光区域进行切割，并记录每一条直线的总长度，对所有线条长度求平均可作为x方向即水平方向上该部分结构的子等效周期。相应地，同样采用数根垂直等间距分布的直线进行切割，计算所有线条的平均长度即可得到y方向即竖直方向上的子等效周期。该方法的核心是以同一通光孔在竖直和水平方向上的平均长度作为这一部分通光孔2个方向上的子等效周期。

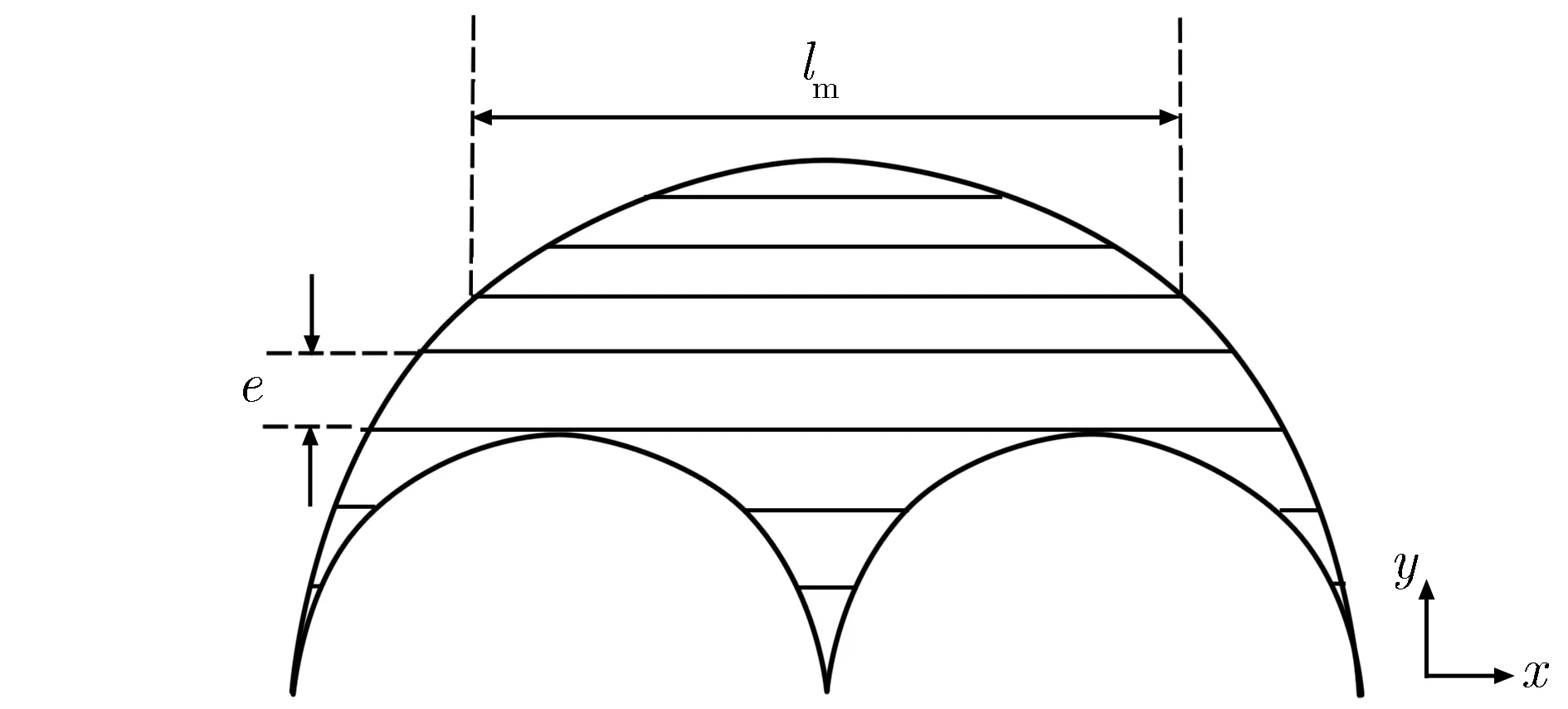
(a) Horizontal

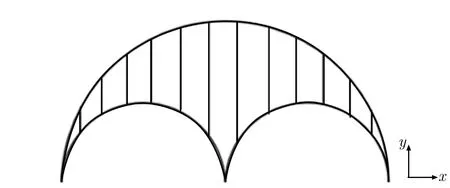
(b) Vertical

假设水平切割直线条数为m，直线间距为e，每条直线在通光孔内部的总长度记为lm。对任意形状的通光孔按上述方法进行计算时，令该通光孔的水平方向子等效周期记为a，竖直方向上的子等效周期记为b。同时，已知该通光孔在水平方向上的最大跨度长度记为b′，在竖直方向上最大跨度长度记为a′。图3为子圆圆环网栅A图形和B图形最大跨度长度示意图。

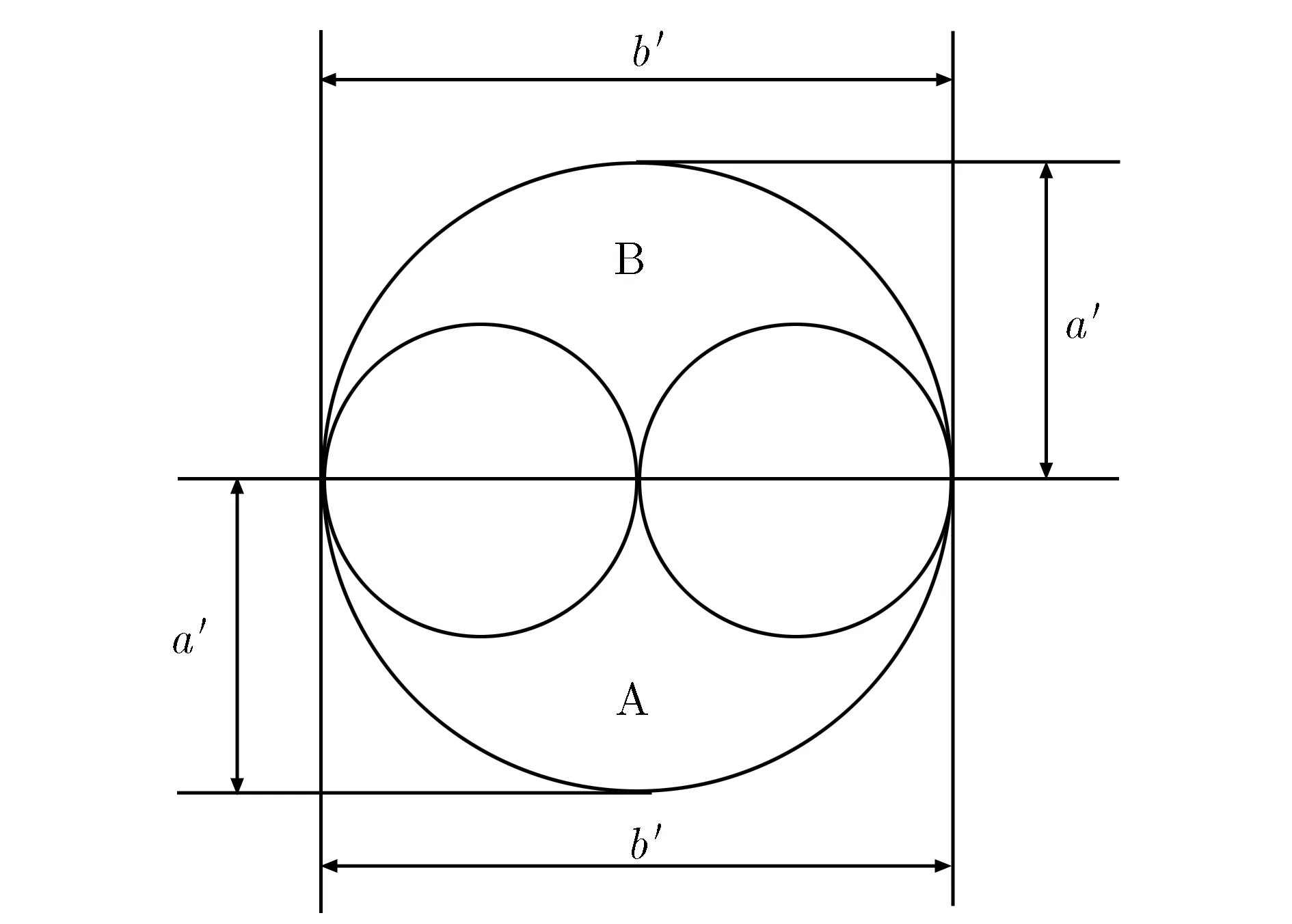
图3 2子圆圆环网栅A图形和B图形最大跨度长度示意图Fig.3 Maximum span length of 2 sub-circular ring grid A pattern and B pattern

以水平切割情况为例，可得到

(15)

其中：Sn为第n条线的矩形面积；ln为矩形的长；直线间距e即为矩形的宽。

由式(15)可知，当具有m条线，线间距为e时，可得到竖直方向上的最大跨度长度a′ =me。根据微积分的思想，将所有以线长lm为长，间距e为宽的矩形面积Sm相加后，即可得到不规则图形通光孔的总面积S，即

(16)

同理，可得到

(17)

因而，对于一个独立透光区域而言，只需知道总面积S和竖直方向最大跨度a′ 及水平方向上的最大跨度b′ ，即可得到水平方向子等效周期a和竖直方向上的子等效周期b。因此，对于给定的任意形状的通光孔，只需知道该通光孔的面积S及该通光孔在水平和竖直方向上的最大跨度长度a′ 和b′ ，即可计算得到该部分图形在水平和竖直方向上子等效周期a和b。

上述方法仅仅是针对多子圆圆环网栅结构的一个独立透光区域获得子等效周期，对一个网栅周期内其余部分图形也可用相同的方法计算获得相应子等效周期，进而根据各部分图形面积在总面积中所占的比例，对求得的所有子等效周期进行加权求和，得到整个金属网栅在水平和竖直方向的等效周期gx和gy。

以3子圆结构为例，结构由2维正交排布圆环作为基本圆环，并在每个基本圆环内添加3个子圆环得到，3个子圆环两两外切。图4为2维正交排布3子圆金属圆环网栅结构。对多子圆圆环网栅，独立通光区域通常包含子圆通光孔、子圆间的镰刀状通光孔、子圆环中间的通光孔(2子圆情况下不存在)及基本圆环(大圆)间的缝隙通光孔4部分。

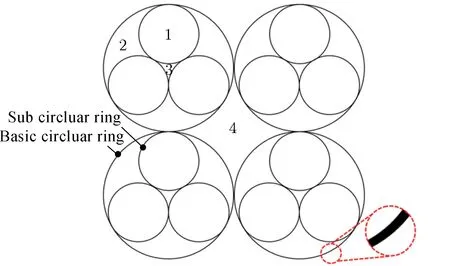
图4 2维正交排布3子圆金属圆环网栅结构Fig.4 2-D orthogonal arrangement of 3-circle metal ring grid structure

定义子圆环间镰刀状(图形2)水平和竖直方向子等效周期为an′和bn′，面积为Sn′，其中n′为子圆数；定义子圆(图形1)的水平和竖直方向子等效周期为aH和bH，子圆图形面积为SH；定义基本圆环间缝隙通光孔(图形4)的水平和竖直方向子等效周期为aW和bW，该部分图形面积为SW；令子圆环中间部分通光孔(图形3)的水平和竖直方向子等效周期为aE和bE,面积为SE。基本圆环阵列确定后，基本圆环间缝隙(图形4)和子圆(图形1)不随子圆环旋转而发生改变，因此这2部分的子等效周期不随子圆环转角改变发生变化。由此便可得到多子圆圆环网栅结构在水平方向和竖直方向上的等效周期gx和gy，表示为

(18)

(19)

其中，n′=2时，nE=0，其余情况，nE=1。

3 多子圆圆环金属网栅屏蔽效率分析与验证

根据第2节提出的等效周期计算方法，可计算得到多子圆圆环网栅的等效周期，带入MERRM模型，结合等效薄膜法，可得到网栅的电磁屏蔽效率模型计算结果，其中带入水平方向等效周期gx的计算结果为TE波入射结果，带入竖直方向等效周期gy的计算结果为TM波入射结果。下面将模型计算结果与CST仿真结果进行对比，为确保数据采集的准确性，计算间隔设为0.006 GHz。

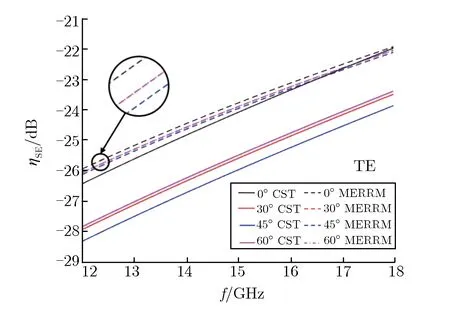
分别采用包含2，3，4子圆环的圆环网栅，并取子圆环逆时针旋转角度θ为0°，30°，45°，60°时4种情况进行研究。分析TE波和TM波入射情况，得到2，3，4子圆圆环网栅在4个转角条件下，模型计算结果与仿真结果的对比，分别如图5、图6和图7所示。

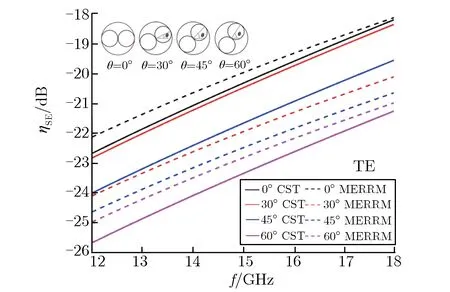
(a) TE wave

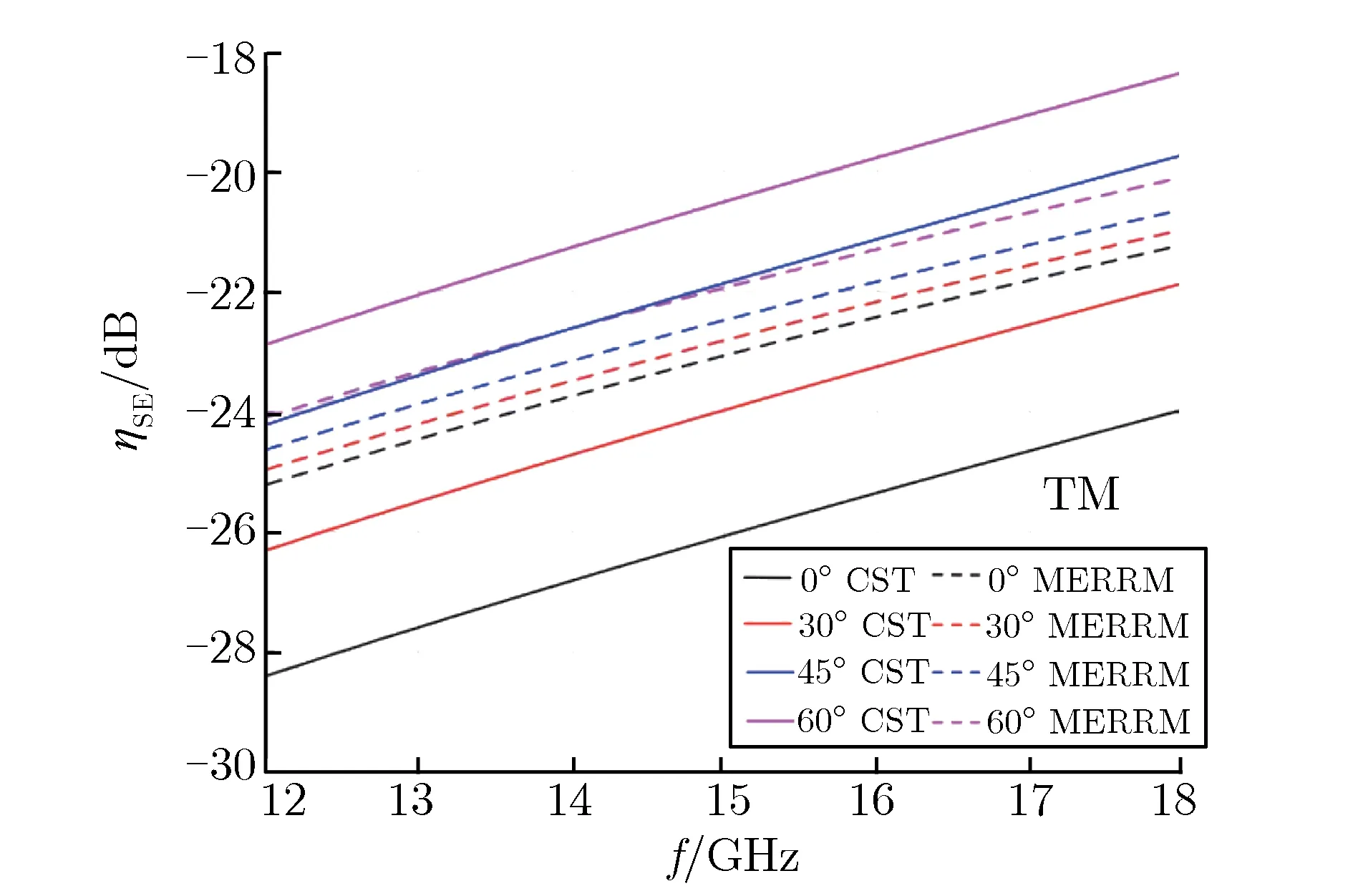
(b) TM wave

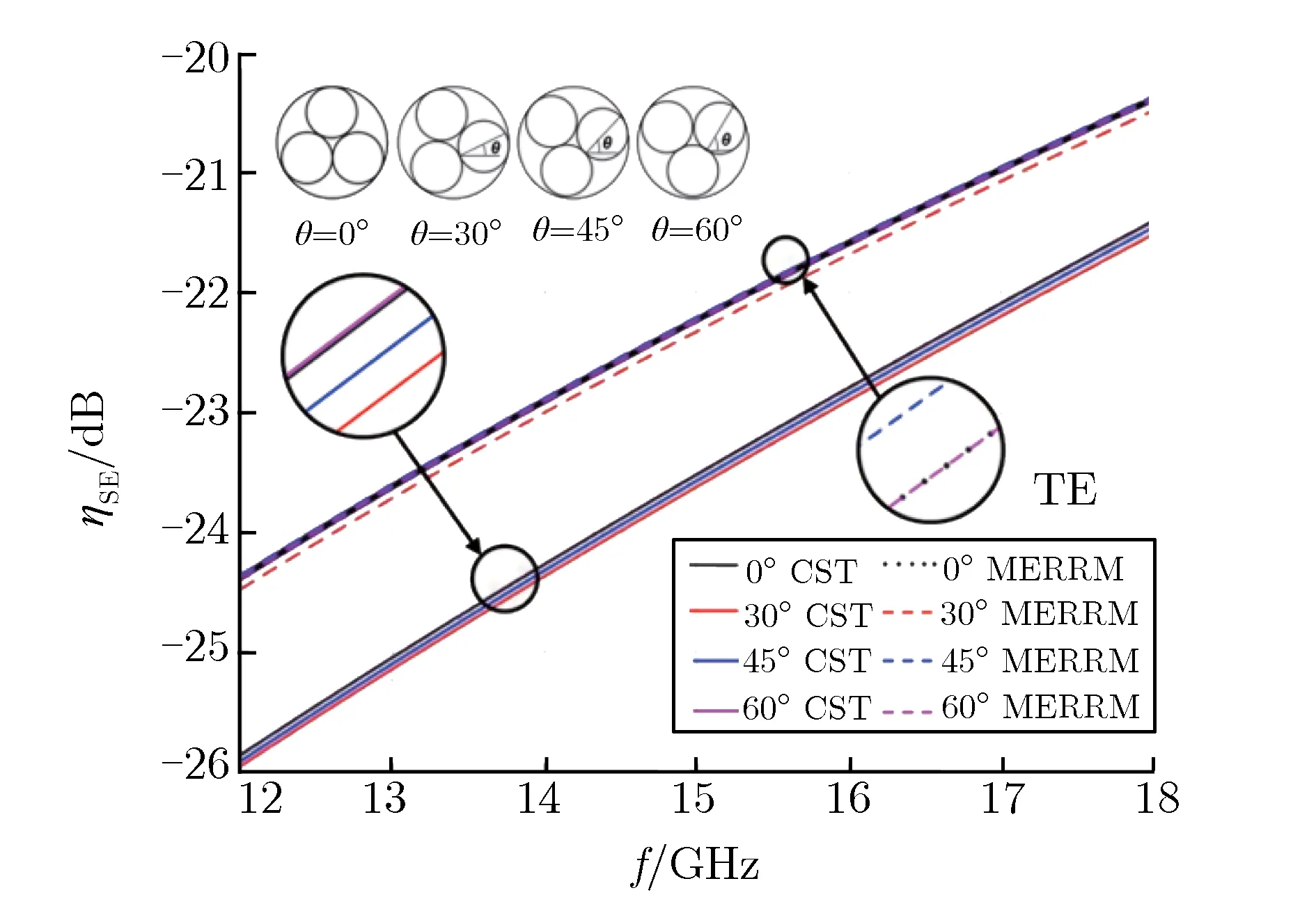
(a) TE wave

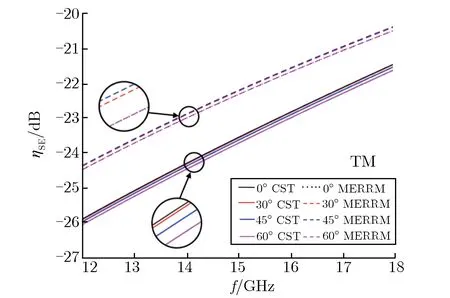
(b) TM wave

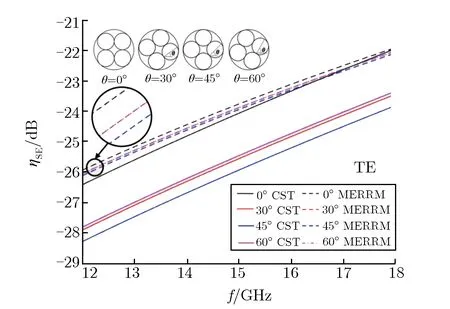
(a) TE wave

(b) TM wave

由图5可见：对于2子圆圆环网栅，当频率为12～18 GHz时，TE波入射与TM波入射，转角相同时，MERRM模型计算结果与CST仿真结果随频率增大变化趋势一致，表现为ηSE绝对值随频率增大而减小；频率相同时，二者随转角增大变化趋势也一致，TE波入射结果表现为ηSE绝对值随转角增大而增大，TM波入射结果与之相反。由以上2点可知，模型计算结果与仿真结果变化趋势相匹配。在ηSE数值方面，任意条件下的一组模型计算结果与仿真结果的偏差都在3 dB范围内，且大部分情况下偏差小于2 dB，说明模型计算结果与仿真结果数值匹配。由图6和图7可见，对于3、4子圆圆环网栅，也能得到相似结论，特别是当子圆环个数增多时，与2子圆圆环网栅相比，入射波偏振态的影响明显要小，2种偏振态下计算结果的偏差较小，且子圆环数量增多时，子圆环空间旋转角的影响也减小，在金属网栅设计时可适当增加子圆环的个数。

在计算效率方面，以4子圆内切圆环网栅结构为例，CST仿真计算耗时83 s，MERRM模型计算方法耗时7.79×10-3s，用时不到仿真过程的0.01%。由此可见，与仿真计算相比，模型计算方法极大地提高了计算效率。

综上，本文提出的等效周期计算方法对于2，3，4子圆圆环网栅，MERRM计算结果与CST仿真结果变化趋势基本一致，且数值计算偏差在3 dB范围内，大部分情况下偏差甚至小于2 dB。因此，验证了该方法对多子圆圆环金属网栅电磁屏蔽效率分析的准确性。而且，本文方法结合等效薄膜法，可实现屏蔽效率快速高效计算，避免了CST方法在计算时间和计算资源上的巨大消耗。

4 小结

本文提出了一种基于面积加权的多子圆圆环金属网栅等效周期获取方法，将等效周期带入传统MERRM模型可快速计算出网栅屏蔽效率，与CST仿真结果对比，二者结果相似，说明了该方法计算屏蔽效率具有较好的准确性。基于该方法，分析了多子圆圆环网栅结构在不同子圆个数、不同旋转角及不同入射波偏振状态条件下ηSE的差异。不同偏振态入射波导致了圆环网栅结构的ηSE略有差异，整体呈现出随着子圆数的增加差异逐渐减小的趋势，且子圆数增多时，子圆环空间旋转角影响减小，因此在金属网栅设计时可适当增加子圆环的个数，以达到更好的屏蔽效果。

致谢

感谢德国CST计算机仿真技术有限公司(CST Computer Simulation Technology Gmb)在哈尔滨工业大学CST培训中心(东北地区)免费提供的CST Studio Suite软件。