级数求和方法的探讨与总结

武 彩 霞

(大同师范高等专科学校，山西 大同 037000)

0 引 言

级数理论是数学分析以及高等数学中的一个重要内容，也是专升本数学必考的一个内容.收敛级数的求和在级数理论体系中占有很重要的位置，既是教学的重点，又是教学的难点.教材中对级数的敛散判别方法讲述的比较多，但是对收敛级数的求和方法介绍的比较少，导致学生在遇到级数求和问题时，常常感到束手无策.级数求和需要用到大学数学中的许多理论知识和运算技巧，是个难度较大，技巧较高的综合性问题，可采用的方法又是多种多样的，只有选用恰当的方法，把级数化归为可求和的形式，才能使问题得到解决.为此，对级数的求和问题进行了探讨与研究，探索级数求和的运算规律，总结出一些常用的级数求和的常规方法与特殊方法，并对每种方法的适用类型、应用技巧、注意事项作了简要分析.以期学习者对级数求和有一个较为全面的认识，从而促进对级数求和问题的学习和理解，并能正确解答级数求和问题.

级数分为数项级数和函数项级数两类，其中，幂级数是函数项级数中最简单的一类，有的数项级数还可以看作与之相对应的函数项级数在自变量取某个常数值而得到的.在幂级数中推导出的级数求和公式，可以直接用在数项级数的求和运算中，而某些数项级数也可以通过一些适当的变换，转化为幂级数来求和.因此，两类级数的求和方法研究不是孤立的，而是相辅相成的.因此，根据级数的类型及特点，对于级数求和的常用方法，分别总结出四种常规方法，四种特殊方法.

1 级数求和的常规方法

对于简单的级数，可以采用裂项相消法、公式法、拆项法、错位相减法等，并借助于四则运算、变量代换、标号代换等恒等变形，直接求出级数的和.

1.1 裂项相消法

若级数的通项为分式，且分母是因式之积的形式，则可将其通项拆成两项之差，把差式关系代入级数的部分和中，在部分和的展开式中，一些正、负项相互抵消，只剩下有限个项，再通过求部分和数列的极限，得出原级数的和.

裂项相消法是利用级数收敛的定义来求和时经常使用的方法，多用于数项级数的求和运算中.

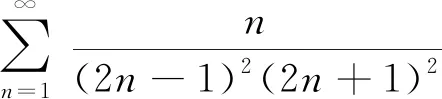
解：由于部分和为

大多数函数项级数的求和比较困难，因为其部分和函数不易求出.如果函数项级数的通项为分式，且分母是因式之积，能够拆成两项之差，把差式关系代入级数的部分和函数中，在部分和函数的展开式中，一些正、负项可以相互抵消，也可以运用裂项相消法求和.

解：由于部分和函数为

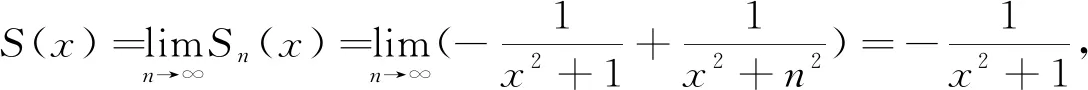
以上两个例题使用裂项相消法的共同目的，就是为了把Sn或Sn(x)化为有限个项，以便求出它们的极限，进而求出级数的和.

1.2 公式法

一些初等函数的幂级数展开式，可以作为幂级数求和公式来使用.仔细观察级数的通项，与类似的已知级数求和公式相对照，将级数经过提取变量、变量替换、拆分组合等方法，转化为相应的已知幂级数形式，代入幂级数求和公式即可求和.

例3(山西省2018年专升本试题)

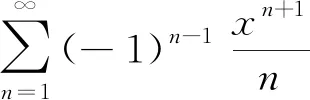
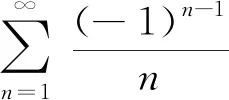
1.3 拆项法

如果级数通项可拆分为有限和的形式，就可以将级数拆分成两个(或几个)简单的收敛级数之和，结合公式法，分别计算各部分级数的和，再求出原级数的总和.

在幂级数求和运算中使用拆项法时，还要注意：既要分别求出拆分后的各个幂级数的收敛半径，又要求出它们公共的收敛半径，并且要求出和函数的收敛域.

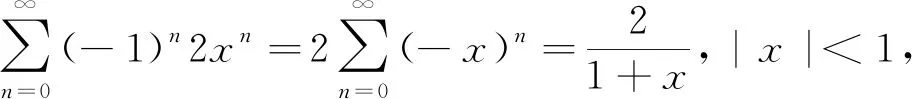
则R=min{1,3}=1，该幂级数收敛域为x∈(-1,1)，

1.4 错位相减法

错位相减法，适用于通项为anbn型的级数求和，其中{an}为等差数列，{bn}为等比数列.先将部分和Sn乘以公比q得到qSn，然后错开一位，与原部分和Sn作差，使得部分和可用等比级数求和公式来计算，从而简化级数求和问题.在计算中要注意：错位相减后，等比数列求和部分的项数变成(n-1)项.

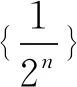
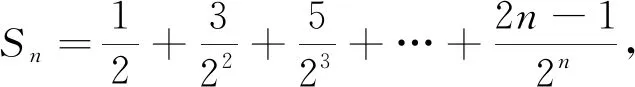
(1)

(2)

由(1)-(2)得

2 级数求和的特殊方法

对于复杂的级数，若采用以上几种常规方法，并不能求出级数的和，则需要采用逐项求积、逐项求导、问题转化、构建微分方程等特殊方法，有时需要综合运用以上几种方法，间接求出级数的和.

2.1 逐项求积法

若幂级数通项系数的分子是自然数，或相邻自然数相乘的形式，则采用先积后导的方法计算.先在收敛区间内使用逐项求积法，约去分子上的自然数，求出新级数的和函数，再对此和函数求导，得出原级数的和函数.

2.2 逐项求导法

分析：这是一个缺项幂级数，用比式判别法的极限形式时，要把通项整体代入，从而求出收敛半径，

则收敛半径R=1，收敛区间为(-1,1).

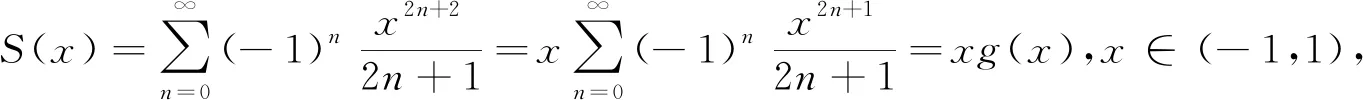
从而S(x)=xg(x)=xarctanx，x∈(-1,1)，

2.3 把数项级数转化为幂级数求和

有些数项级数的表达式比较复杂，无法直接用已知公式求和，可以根据级数中各项的变化规律，构造一个容易求和的幂级数，使数项级数是此幂级数在某个收敛点x0处的值，求出幂级数的和函数S(x)，代入x0，则S(x0)就是该数项级数的和.

由于S′(x)=1+x-x3-x4+x6+x7-x9-x10+…

=(1+x)-x3(1+x)+x6(1+x)-x9(1+x)+…

当x=±1时，该级数收敛，其和函数S(x)在点x=-1处右连续，点x=1处左连续，

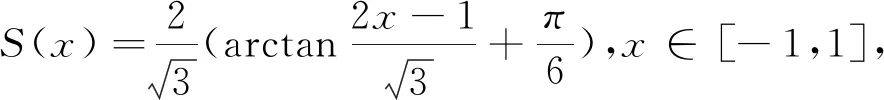
2.4 微分方程法

则R=+∞，收敛域为(-∞,+∞).

从而S′(x)=-S(x)+ex，

(3)

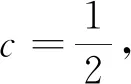
3 结 语

级数求和问题，是高等数学中的一个难度较大的问题，没有一定之规可循.要解决一般的级数求和问题，需要掌握上述级数求和的八种常用方法，还要熟记一些常用的幂级数求和公式.对于更为复杂的级数求和问题，则需要综合运用其中的几种方法，或寻求其它方法，才能有效地解决问题.