基于阶段生长PGSA的索穹顶结构预应力优化

姜正荣 苏延 石开荣† 李之吉 魏德敏

（1.华南理工大学土木与交通学院，广东 广州 510640；2.华南理工大学亚热带建筑科学国家重点实验室，广东 广州 510640）

索穹顶是由美国工程师Geiger等［1］提出的一种连续拉、间断压的柔性张力结构体系，具有极高的结构效率，目前已成功应用于众多大型体育场馆中［2-4］。索穹顶结构在自然状态下呈松弛状，不具有刚度，施加预应力方可使其产生刚度并抵抗外荷载，且预应力的大小与分布决定了结构形状与结构刚度［5］。因此，对该类结构进行预应力优化具有十分重要的科学意义。

国内外学者对索穹顶结构的预应力优化进行了相关研究，并取得了一系列成果。文献［6］采用遗传算法，分别以结构自重最小及竖向位移最小为目标，完成了索穹顶结构的预应力优化。文献［7］采用NSGA-II遗传算法，对Kiewitt型索穹顶结构进行多目标优化，得到了最优自应力模态组合系数。文献［8］对Geiger型索穹顶结构的单目标及多目标的不同优化算法进行了对比分析，并探讨了各种算法的适用范围。

模拟植物生长算法（Plant Growth Simulation Algorithm，PGSA）是一种基于植物向光性机理的新型智能优化算法［9］，自提出以来已应用于多个行业的优化分析，并逐步加以改进。文献［10］采用非支配排序及构造偏序集等方法对PGSA进行改进，并对多目标旅行商问题进行了求解，对比其他优化算法更具有优势。文献［11］对形态素浓度的计算及新增点的生长策略进行了改进。文献［12］采用PGSA对RFID网络规划模糊覆盖问题进行了研究，指出了该方法的有效性。文献［13］在重新初始化、搜索步长、算法终止判据等方面对PGSA进行改进，并应用于电子干扰资源分配的优化中。近年来，PGSA在工程结构优化领域得到发展与应用，如高层悬挂结构［14］、桁架结构［15］及弦支穹顶结构［16］等。

但是截至目前，涉及PGSA在索穹顶结构优化方面的研究尚鲜见报道，鉴于此，本研究针对原算法的局限性，提出新策略，在此基础上，建立阶段生长PGSA，以此对索穹顶结构进行预应力优化，并与其他算法进行对比，验证其适用性。

1 PGSA基本原理

根据植物生长的原理，PGSA将工程结构优化问题的约束空间视为植物的生长空间，将目标函数视为光源。首先在生长空间内选取一粒种子，即初始生长点x0，其对应一个初始函数值f(x0)；然后采用一定的步长，在初始生长点的附近产生节，即下一批可生长点Sm，i（其中i为生长点序号），计算每个可生长点所对应的函数值f(Sm，i)，并剔除大于f(x0)的点，最终组成可生长点集合Sm。通过对比该集合中可生长点函数值与初始函数值之间的差距，给予相应的形态素浓度。函数值越优于初始函数值的可生长点，其对应的形态素浓度越高，反之则越低，形态素浓度的计算如式（1）所示：

式中，k为集合Sm中可生长点的个数，Pm，i为第i个可生长点的形态素浓度。

在可生长点集合Sm中，其形态素浓度之和满足：

所有形态素浓度构成了一个概率区间[0，1]，每个可生长点对应一部分区域，通过随机搜索的方式选择其中一个区域，将对应的点作为下一次生长点，如图1所示。可生长点的函数值越靠近目标，其形态素浓度越高，所对应的概率区域越大，那么被选为下一次生长点的概率相应就越高。通过这种形态素生长机制，使该植物的枝节反复生长，直到搜索到光源的位置，即函数的最优解。

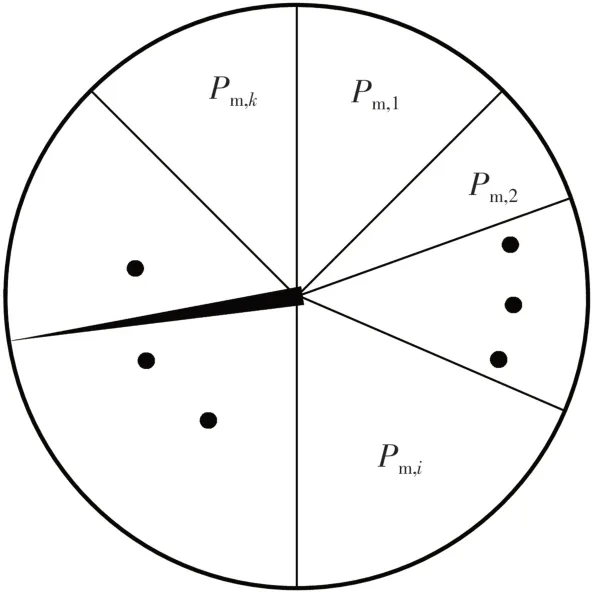
图1 形态素浓度及其对应的生长概率Fig.1 Morphactin concentration and its growth probability

2 PGSA新策略

从多段步长搜索及生长机制等方面，探讨原PGSA的局限性。参考文献［17］，以具有两个独立变量的Rastrigin函数为测试算例（图2），其表达式为

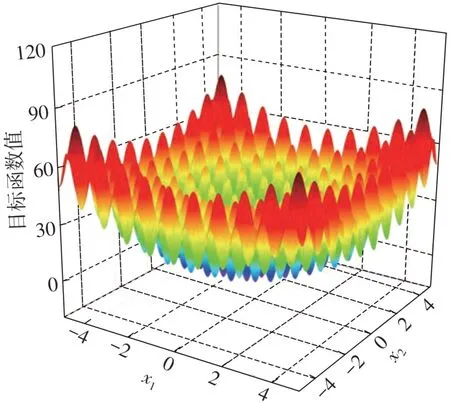
图2 目标函数三维视图Fig.2 Three-dimensional view of objective function

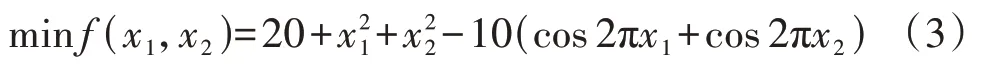
式中：f(x1，x2)为目标函数，即模拟植物生长的光源，两个设计变量分别为x1、x2，将可行域设为-5≤x1，x2≤5，以函数的全局最小值为优化目标，精度为0.1。

由图2可见，该函数有非常多的局部极小点，但仅有一个全局最优解，即x1=x2=0，此时函数值f(x1，x2)=0，达到最小。下文分析中，以图2的函数为基础，对不同参数取值分别运行50次，并记录其优化得到的最小目标函数值的均值及平均生长空间（平均生长点数量），以此对比不同优化机制的优化效果与效率。

2.1 原算法的局限性

2.1.1 步长机制

为探讨原PGSA的局限性，在此提出多段步长生长机制，即采用非固定的步长进行生长，并与常规的单一步长生长机制进行对比。限定最大生长次数为1 000，分别采用原PGSA的单一步长（步长为0.1）、两段步长（大步长为2，生长10次，小步长为0.1）及三段步长（大步长为2，生长10次，中步长为0.5，生长100次，小步长为0.1）进行优化分析，结果见表1，优化效果曲线如图3所示。

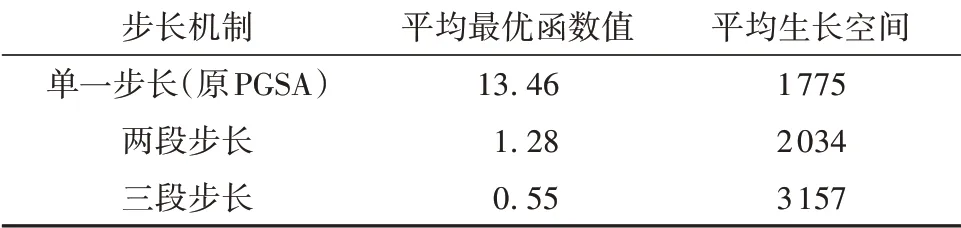
表1 各步长机制的优化结果Table 1 Optimization results of each step mechanism

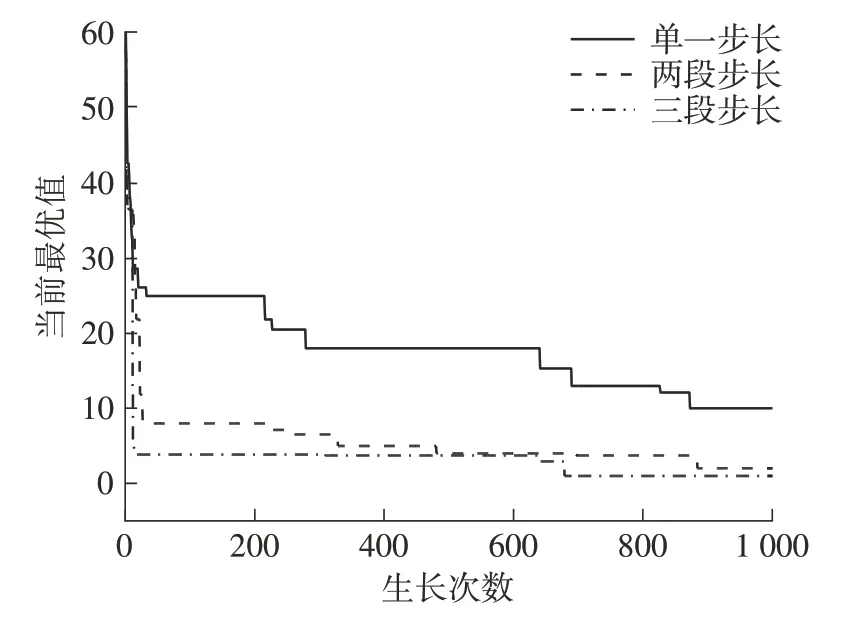
图3 各步长机制的优化效果曲线Fig.3 Curves of optimization effect of each step mechanism

由表1及图3可见，与原PGSA的单一步长相比，两段和三段步长的平均最优函数值较小，且后者更接近全局最优解，但随着步长段数的增加，生长空间也随之迅速扩大。由此表明，采用多段步长生长可提高PGSA的全局搜索能力，但在缺乏有效筛选机制时，该方法必然会增加计算工作量。

2.1.2 生长点分布

在多段步长生长机制的基础上，进一步研究大步长生长次数对优化结果的影响。以两段步长PGSA为例，同样采用大步长为2，小步长为0.1，分别以大步长生长1次与30次进行对比，优化结束后生长点的分布如图4所示。在此将以大步长生长产生的点称为大生长点。

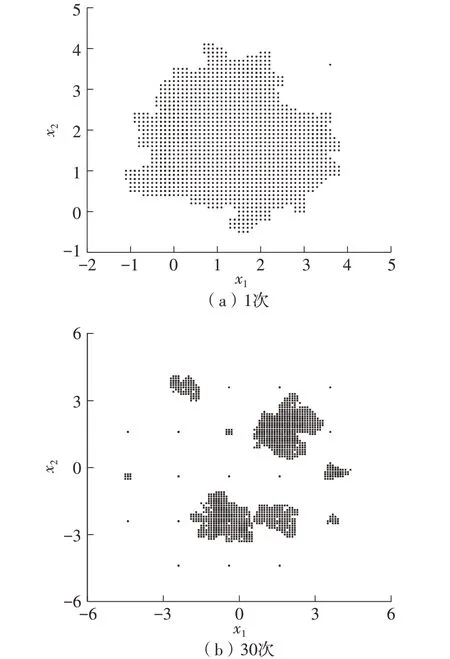
图4 不同大步长生长次数的生长点分布Fig.4 Distribution of growth points with different growth numbers of large step

由图4可见，当大步长生长1次时，大生长点仅分布在x1，x2∈(-2，4)区间内，未能扩散至整个可行域，其全局搜索能力较差；当大步长生长30次时，大生长点扩散至x1，x2∈(-5，5)的范围。当大生长点以大步长为间距完全充满整个可行域，即达到饱和后，每次生长得到的点均会与原有的大生长点重复且被忽略，使该生长点无法在后续以小步长进行生长，从而形成了一片无效区域，生长点无法在其中扩散。由此表明，大步长具有散播生长点、提高全局搜索能力的作用，但若生长次数过多，使其达到饱和后，则反而会弱化全局搜索能力，影响优化结果。

2.2 算法新策略

基于上文分析，从大步长生长扩散机制及生长点筛选机制两方面，提出PGSA的新策略。

2.2.1 大步长生长扩散机制

针对大步长生长次数过多而导致生长点饱和的问题，对大步长采用多倍步长一次性扩散的方式以替代原PGSA中的随机渐进扩散。如图5所示，按原生长机制，初始生长点将向两个维度进行步长为dx的生长，从而产生8个新增的生长点，可跨越2倍步长（2dx）的空间，下一次将从新增生长点中随机选择一个生长点，并重复该生长流程，直至生长点布满整个可行域。多倍步长一次性扩散生长则分别以1～n倍步长进行生长。以3倍步长一次性扩散生长为例，其将向两个维度分别以1、2及3倍步长（3dx）的距离进行一次生长，便可产生48个新增的生长点，所跨越的距离达到6倍步长（6dx）。由于不再进行随机生长，所有的生长点均不会被淘汰。通过该生长扩散机制，并选择合适的大步长，便可得到布满整个可行域的大生长点，起到了散播生长点的作用，且避免了生长点的过早“废弃”。

图5 大步长生长扩散机制Fig.5 Growth diffusion mechanism of large step

2.2.2 生长点筛选机制

在此引入筛选系数w与筛选空间Sw，在每一次搜索时，对已求得的函数值从优至劣进行排序，得到筛选集合R，以该集合中排在第q位的函数值为对比指标，即f(Rq)，其中q=Sw×w。将函数值比该对比指标差的新增生长点剔除，以此控制生长空间的规模。在搜索到全局最优解之后，该筛选机制会使可生长点集合逐渐缩小直至无可生长点，从而达到快速收敛并停止运算。

3 阶段生长PGSA

3.1 算法机制及其计算流程

依据上述新策略，提出了基于阶段生长的模拟植物生长算法（阶段生长PGSA），即将植物生长分为多个阶段，并在不同阶段引入相应的生长扩散机制或生长点筛选机制，从而实现该算法的快速收敛，并提高全局搜索能力。

其基本思路为：对初始生长点x0采用大步长进行搜索，并以3倍步长一次性扩散生长，得到布满整个可行域的生长点；随后以中步长进行快速搜索，配合较宽松的筛选机制，以控制生长点的数量；最后以与精度相同的小步长，结合较严格的筛选机制，从而达到快速收敛的目的，且在搜索到满足精度要求的全局最优解后及时终止计算。

该算法流程如图6所示，具体步骤如下：

步骤1定义初始生长点x0，并定义大、中、小步长及其对应的生长次数、筛选系数w与筛选空间Sw。

步骤2计算得到初始生长点x0对应的目标函数值f(x0)，以此作为全局最优函数值Fmin的初始值。

步骤3在不同阶段选择不同的步长，对新增生长点对应的函数值f(Sm，i)进行排序，以排在第q位的函数值f(Rq)为对比指标，其中q=Sw×w；将函数值劣于筛选标准(f(Sm，i)＞f(Rq))的新增生长点剔除，其余则加入可生长点集合Sm中。

步骤4判断可生长点集合是否为空集，若为空集，则跳转至步骤8，若不为空集，则继续进行下一步。

步骤5找出当前次新增生长点对应的最优函数值fmin，与既有全局最优函数值Fmin对比，判断是否为更优，若是，则更新全局最优函数值Fmin及其对应的最优生长点Xmin。

步骤6对生长点集合中所有的可生长点按式（1）计算形态素浓度，并按概率随机选取下一次的生长点。

步骤7判断是否达到最大生长次数，若未达到，则回归步骤3继续进行优化，若达到，则进行下一步。

步骤8输出最终搜索得到的最优函数值Fmin及其对应的最优生长点Xmin，结束优化流程。

3.2 算例分析

仍以式（3）所示的Rastrigin函数为例，基于图6的流程进行优化。设置大步长为2，以3倍步长进行一次性扩散，中步长为0.5、生长100次，小步长为0.1，最大生长次数为1000。中、小步长对应的筛选系数分别为0.8、0.4，筛选空间均为100。对文中提出的阶段生长PGSA（三段步长+扩散机制+筛选机制）与纯多段步长PGSA（两段步长及三段步长）及原PGSA的单一步长的优化结果进行对比，如图7所示。

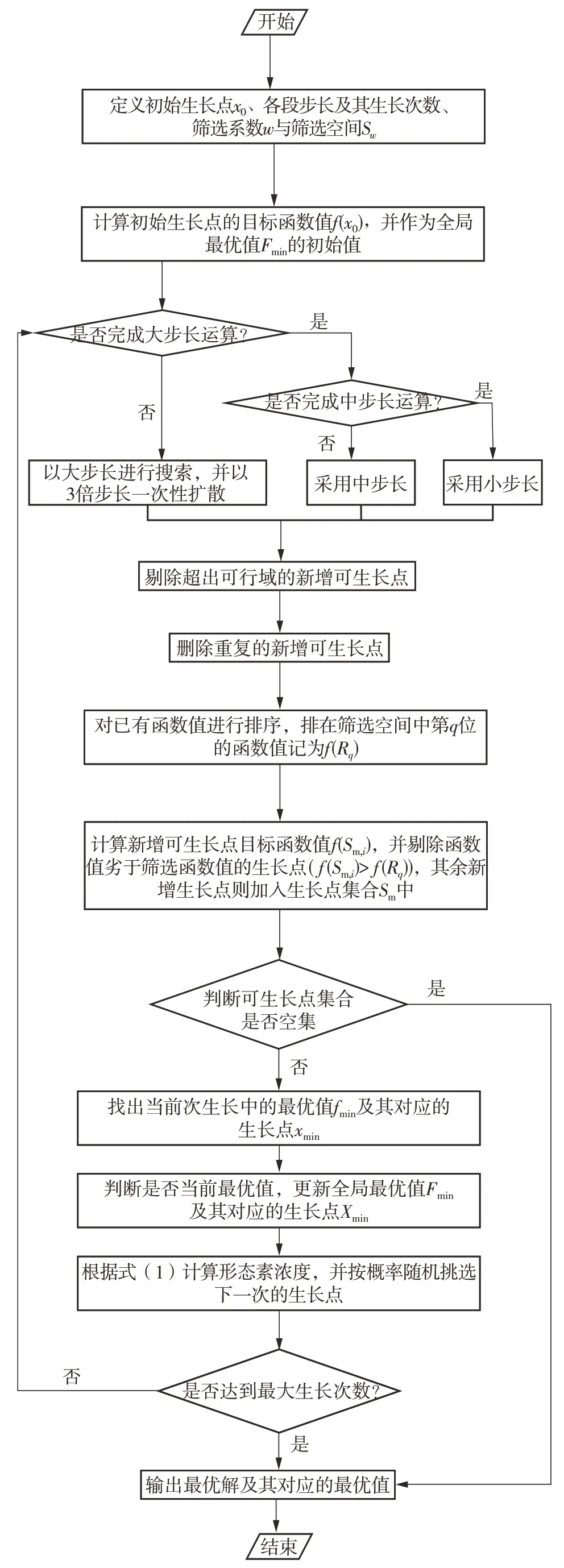
图6 阶段生长PGSA流程图Fig.6 Flow chart of stage growth PGSA

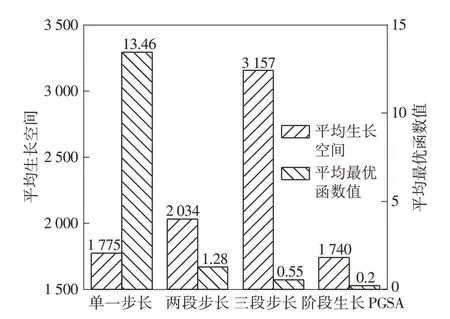
图7 不同PGSA的优化结果Fig.7 Optimization results of different PGSA

由图7可见，阶段生长PGSA通过大范围生长，在提高全局搜索能力的同时避免了生长点的饱和，且由于筛选机制的引入有效地缩小了生长空间，其平均最优函数值及平均生长空间均优于原PGSA。

4 索穹顶结构的预应力优化

在上文分析的基础上，对索穹顶结构的预应力进行优化。该结构的预应力优化有两个特点：一是搜索域中存在大量无解的点，二是最优解相对集中于某些区域。阶段生长PGSA可通过大步长有效跨越这些无解空间，再通过中步长与小步长快速搜索有解的空间，从而提高优化效率。因此，相比于其他优化算法，当阶段生长PGSA应用于索穹顶结构的预应力优化时，其具有显著的优势。

4.1 优化模型

为验证阶段生长PGSA在结构优化中的适用性，以某实际工程为背景，构建图8所示的复合型索穹顶结构，对其进行预应力优化（标高单位为m，其余单位为mm）。结构跨度为100m，矢高为7.5m，设有内拉环及两道环索，周边固定铰支座。拉索采用弹性模量为195 GPa的平行钢丝束；撑杆及内拉环采用Q355B钢材，弹性模量为206 GPa。结构的自应力模态数为2，构件截面面积及各组自应力模态如表2所示。

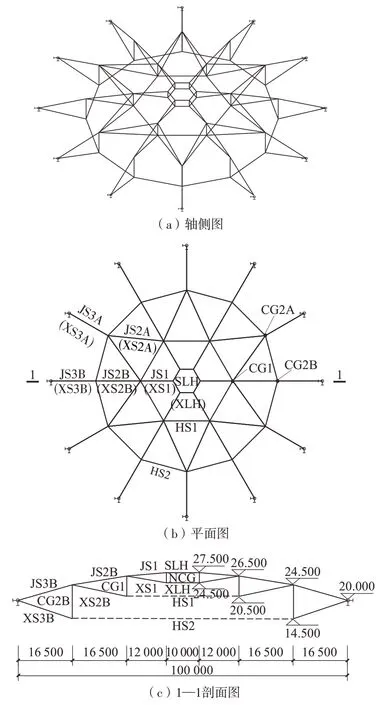
图8 优化模型Fig.8 Optimal model

4.1.1 优化变量

将表2中的两组自应力模态记为{X1}和{X2}，并将其与组合系数β1、β2相乘，叠加得到最终的结构初始预应力{T}，如式（4）所示。以该组合系数β1、β2为优化变量。

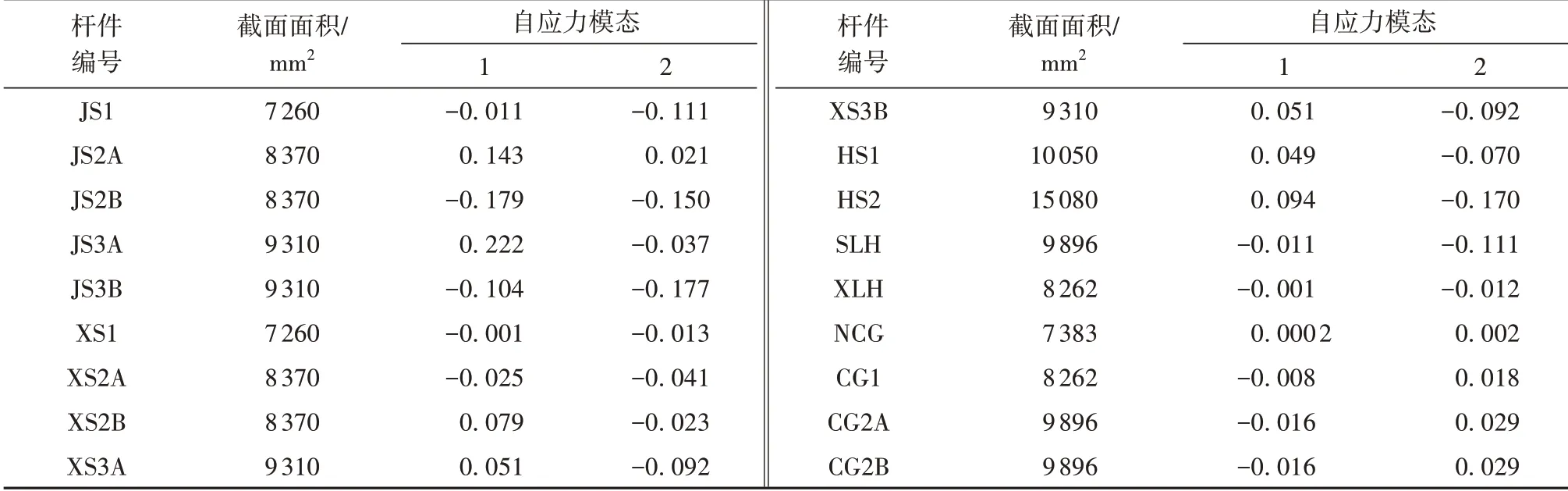
表2 构件截面面积及自应力模态Table 2 Section areas and self-stress modes of members

4.1.2 目标函数

当索穹顶结构张拉完成时，结构的应变能由张拉设备所提供，在满足约束条件下，应变能越小，张拉设备所做的功越少，张拉难度越低，施工越方便，其对应的经济效益越好。因此，在确定自应力模态组合系数时，以结构的初始应变能最小为优化目标：

式中，Ti为第i类杆件的初始预应力，n为结构的杆件类别数，Ei、Ai、li分别为第i类杆件的弹性模量、截面面积及长度，ni为第i类杆件的同类杆件数量。

4.1.3 约束条件

（1）整体可行性

由组合得到的初始预应力，应满足索受拉、撑杆受压且同一圈同类杆件预应力相等的整体可行性。这是索穹顶结构的自有特性，即依据节点平衡条件，索仅受拉力，撑杆仅受压力，且所有杆件的受力均满足对称性。

（2）刚度要求

荷载态时，在自重、附加恒载0.5 kN/m2及不上人屋面活载0.3 kN/m（2全跨布置）的共同作用下，结构的最大节点竖向位移不大于跨度的1/400，荷载组合为1.0恒载+1.0活载的标准组合。

除上述约束条件外，还需对拉索的强度、撑杆的强度及稳定性进行验算。限于篇幅，在此不再赘述，具体详见文献［18］。

4.2 优化结果与分析

基于上文提出的阶段生长PGSA，通过MATLAB与ANSYS的协同编程实现参数化建模、结构计算以及优化算法的执行。将阶段生长PGSA的优化结果与纯多段步长PGSA（两段步长及三段步长）进行对比，参数设定见表3，最大生长次数为1000，筛选空间均为100。经试算，该设定参数下，优化效率及优化效果均较佳，其优化效果曲线如图9所示。

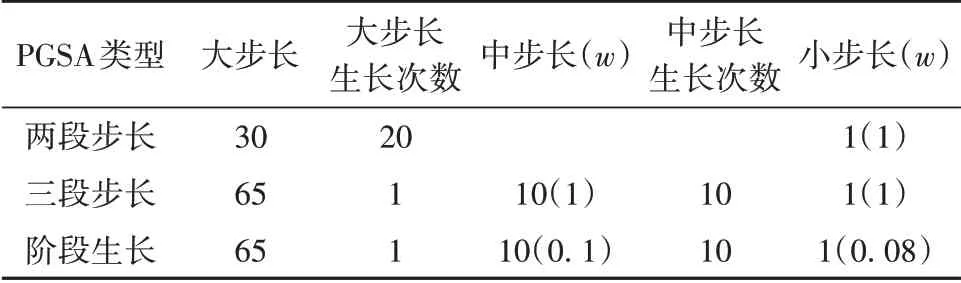
表3 不同PGSA的参数设定Table 3 Parameter setting for different PGSA

图9 不同PGSA的优化效果曲线Fig.9 Curves of optimization effect of different PGSA

由图9可见，采用纯多段步长PGSA（两段步长及三段步长）搜索时，其生长至1000次仍未搜索到全局最优解；阶段生长PGSA运行至第286步便搜索到全局最优解（对应的结构初始应变能f=892.58 kN·m），且在第351步迭代终止。

进一步地，将阶段生长PGSA与多岛遗传算法（MIGA）、自适应模拟退火算法（ASA）及粒子群优化算法（PSO）等优化方法进行对比，优化效果曲线如图10所示（不同算法的每次计算迭代时间基本一致，其关键参数设定详见文献［18］）。

图10 不同算法的优化效果曲线Fig.10 Curves of optimization effect of different algorithms

由图10可见，与其他优化算法相比，阶段生长PGSA的计算迭代次数最少，优化得到的结构初始应变能也最小（分别为MIGA的39.7%、ASA的58.9%及PSO的84.1%）。由此表明，该算法具有更高的优化效率及更好的优化效果，从而验证了其适用性。此外，以阶段生长PGSA求得的全局最优解为β1=58×105，β2=-145×105。荷载标准组合下，结构的最大节点竖向位移为247.3 mm，小于结构跨度的1/400（250 mm）。由组合得到的初始预应力如表4所示，满足索受拉、撑杆受压的整体可行性要求，且拉索的强度、撑杆的强度及稳定性验算，均满足相关规范的要求。

表4 阶段生长PGSA优化后的初始预应力Table 4 Initial prestress obtained by stage growth PGSA

5 结论

（1）相比原PGSA的单一步长，多段步长生长机制可提高PGSA的全局搜索能力，但随着步长段数的增加，其计算量相应增大；当大步长生长次数过多时，易造成生长点的饱和，产生无效搜索区域，从而影响优化结果。

（2）针对原PGSA的局限性，提出了阶段生长PGSA，将优化过程分为多个阶段，先引入大步长生长扩散机制，以多倍步长一次性扩散生长的方式实现生长点的散播，再以中步长配合较宽松的筛选机制进行快速搜索，最后以精度要求的小步长与较严格的筛选机制进行收敛。结果表明：与原PGSA相比，阶段生长PGSA可有效增强全局搜索能力、缩小生长空间且避免了生长点饱和的问题。

（3）采用阶段生长PGSA对索穹顶结构进行预应力优化，并与多岛遗传算法、自适应模拟退火算法及粒子群优化算法等优化方法进行对比。结果表明：阶段生长PGSA的计算迭代次数最少，优化得到的结构初始应变能最小，表现出更高的优化效率及更好的优化效果，由此验证了该算法对索穹顶结构预应力优化的适用性。