粗糙度对冻土-结构接触面剪切特性的影响研究*

陈航杰 何 菲 王 旭 陈明伟

(兰州交通大学土木工程学院，甘肃省道路桥梁与地下工程重点实验室， 兰州 730070)

在岩土工程领域，土体与结构接触面的相互作用普遍存在，接触面力学特性对建、构筑物稳定性和服役期安全性起到关键性作用。随着西部大开发和振兴东北战略的实施，各种寒区工程得以大量修建，随即产生了一系列冻土与结构面的接触问题。冻土受温度的影响较为敏感，且伴随着冻结、融化作用，寒区基础与冻土的接触面力学特性与常温条件下相比差异较大。在冻土-结构接触面剪切试验中，结构粗糙度是影响接触面剪切特性的重要因素之一[1]。国内外学者已对考虑粗糙度的接触面剪切特性方面做了一系列工作：Uesugi等研究了砂粒在不同粗糙程度刚性表面剪切变形特性[2]；Roman等研究了无黏性土与刚性带肋结构面间剪切特性，证明肋间距控制着剪切带的发展状态[3]；王天亮等研究了规则型接触面粗糙度对抗剪强度及抗剪强度参数、剪胀性、应变软化的影响[4]；吉延峻等通过直剪试验进行了现浇混凝土与冻土接触面强度等力学特性的研究[5]。赵联桢等研制了可实现单调和循环加载的多功能大型直剪系统，对接触面力学特性进行了探究[6]；孙厚超等研究了接触面剪切的宏观和微观机理，并建立了耦合粗糙度的剪切强度经验表达式[7]。ALDAEEF等利用直剪试验研究了粗糙度对冻结砂土与钢接触面抗剪特性的影响[8]。

基于已有的研究成果，为对粗糙度对结构-接触面力学特性的影响开展进一步探索，对粗糙度对接触面的影响机理展开研究，以构建考虑粗糙度影响的接触面剪应力-剪切位移本构模型，为深入探讨粗糙度对冻土-桩力学特性的影响提供参考。

1 接触面力学特性试验研究

1.1 粗糙度的定义和评价

冻土-混凝土接触面类型影响着基础结构整体的强度、稳定性，甚至会导致不同破坏类型的产生。其中，接触面粗糙度是决定冻土-结构体接触面力学特性的重要因素之一。按结构物表面的起伏状况、排列方式和形状特征等规律，可以将接触面的粗糙度划分为两大类，即“随机型”和“规则型”[9]。

研究初期，以“随机型”粗糙度为主，常采用随机的表观特征描述结构粗糙度，可采用不同水灰比现浇结构[5]、对预制试块结构面进行不同程度打磨[10]、直接采用不同目数的砂纸[11]等方法来实现粗糙度。对于“规则型”粗糙度，常采用标准的表面齿状结构，通过调整表面齿状结构的峰谷距(如表1中①、③截面)、形状(如表1中①、②截面齿槽的腰角采用锐角[12-13]或直角[6-7,13])和排列方式来改变结构表面粗糙度。也可直接采用竖直[3-4]或半圆形[14]凹槽(如表1中④、⑤截面)，通过调整凹槽数量、宽度和深度达到调整粗糙度的目的。

表1 粗糙度的定义和评价Table 1 Definitions and evaluations of roughness

为分析不同粗糙度的效果，需要将粗糙度进行分类并量化，常用的粗糙度评价方法有直接定义法、表观描述法、试验测定法(灌砂法、触针法、硅粉堆落法、分形分维法)和间接计算法等。对于“规则型”接触面：通常采用的方法是直接定义法，定义起伏界面的峰谷距最大值或齿边长为界面粗糙度[6-7,12]，也可用归类定量法[4]对粗糙度进行定义和测定，或者利用灌砂法，以及金子豪等为“规则型”接触面提出的基于“强度意义”[9]的粗糙度评价方法，该方法充分考虑了凹槽的相关几何参数以及修正槽宽和凹槽对土体的扰动范围等因素；王海航等为了将各种界定“规则型”粗糙度的方法统一量化[15]，提出了基于扩面度的粗糙度计算方法。对于“随机型”接触面：灌砂法较为常用，以体积转化的方法来测定接触面粗糙度，也可以采用触针法通过触针记录表面的凹凸曲线，测得峰谷距的最大值[16]或均方根值[17]来表征粗糙程度，有时也采用统计学中的概率统计方法进行描述[18]，或采用相对粗糙度的定义，以粒径大小评价粗糙度[1-2,19]，再或直接表观描述粗糙度[5,20]。

1.2 粗糙度对接触面强度特性的影响

接触面的力学特性是指在剪切过程中，接触面所具有的力学规律、应力-应变关系、抗剪强度及抗剪强度参数等，粗糙度是这些接触面力学特性的重要影响因素[1]。

1.2.1应力-应变关系及强度

接触面剪切应力-应变关系是建立接触面本构模型的重要力学关系之一[21]。从开始剪切到破坏经历三个阶段，分别为弹性变形阶段、剪切破坏阶段和残余强度稳定发展阶段[5]，如图1所示(粗糙度定义量化方法见文献[7])。可以看出弹性变形阶段的曲线主要呈线性，冻土在此阶段产生弹性变形。剪切破坏阶段试样破坏之后，剪应力起初逐渐变小，“规则型”接触面在剪切过程中剪应力出现变大现象，且呈周期性、跳跃性，存在波动幅度持续降低的次峰值，分析是由于接触面凹凸起伏造成的应力集中现象所致，而“随机型”接触面在剪切位移持续增大且接触面范围减小时，剪应力一直处于相对平缓状态，以上两种情形均为稳定发展阶段。

—0.3 mm； —0.8 mm； —1.4 mm。图1 不同粗糙度下接触面τ-δ关系[7]Fig.1 The curves between shear stress and shear displacement of contact interfaces in different roughness

对冻土与结构接触面的抗剪强度研究可以追溯到苏联时期，土与结构接触面上的冻结强度可用抗剪强度来度量，通过压入或拔出冻土中的竖杆测得抗剪强度[22]。邱国庆等提出：冻土与基础间的冻结力为其接触面上的抗剪力，而冻结强度是土与基础接触面所能承受的最大剪应力[23]。冻结强度分为极限强度和残余强度两大部分[24]。极限强度为剪切过程中的峰值剪应力，即所谓的冻结强度。“规则型”接触面中残余强度为破坏后的次峰值剪应力，其值随剪切位移呈周期性波动，“随机型”接触面中残余强度则呈稳定发展状态。两者均趋于一个稳定值。

冻结强度与冻土-结构接触面的粗糙度有着非常紧密的联系。在冻黏土-结构接触面单剪试验中，试样尺寸长、宽分别为200，100 mm，剪切盒底部及四周采用冷却管隔绝外界环境，保持盒体内恒低温，试验温度分别为-6，-10，-14 ℃，控制精度可达±0.3 ℃[25]。在剪切初始阶段，接触面的极限冻结强度随着接触面粗糙度的增大而增大。在其他因素不变的情况下，随着粗糙度的不断增大，峰值强度先增长较明显，随着粗糙度的进一步增大，峰值强度增长缓慢，Huck等得出类似的结论[26]。如图2所示，数据和粗糙度定义法均见文献[10]。在稳定剪切阶段，接触面的残余强度受粗糙度大小的影响较小。粗糙度只影响峰值强度之前的阶段，对其之后的残余强度影响较小或无明显影响[18]。

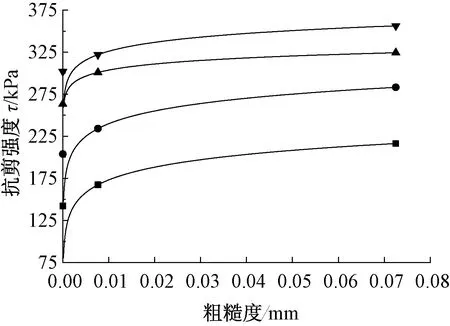
100 kPa； 300 kPa； 200 kPa； 400 kPa； ——拟合线。图2 不同法向压力下接触面抗剪强度与粗糙度关系Fig.2 The curves between shear strength and roughness of contact interfaces under different normal loads

根据以上规律，类比常温情况下土与结构接触面直剪试验[27]中对于峰值强度最优的临界粗糙度。可以推断出：在负温情况下，也可以寻找出对抗剪强度最优的接触面粗糙度值。

1.2.2对抗剪强度参数的影响

粗糙度对内摩擦角φ和黏聚力c有着显著的影响。对于“规则型”接触面，在恒定负温直剪试验[4]中，试样为带凹槽钢板与土结合体，直径为61.8 mm，高为20 mm，钢板、土体高均为10 mm，试验温度分别为-2，-5，-8 ℃，为保证恒定负温，试验在高低温环境控制试验箱中进行。根据拟合的强度曲线得到对应的抗剪强度参数值。在一定的冻结温度条件下，随着粗糙度的增大，土与结构接触面间的抗剪强度参数的变化如图3所示(粗糙度定义法见文献[4])。根据抗剪强度参数与接触面凹槽的曲线可知:随着凹槽条数增多，冻土与结构的接触面积增大，引起黏聚力随粗糙度增大呈增大的趋势。随着凹槽条数的增大，土体颗粒与结构间的摩擦作用增强，但是这种摩擦作用并不会随着凹槽数量的增多而持续增大，而是随着凹槽数量的进一步增多而有所减少，这也印证了粗糙度与接触面抗剪强度关系中最优粗糙度的存在性。

a—黏聚力变化规律； b—内摩擦角变化规律。 -2 ℃; -5 ℃; -8 ℃； ——拟合线。图3 接触面抗剪强度参数与凹槽条数的关系[4]Fig.3 Relations between shear strength parameters of contact interfaces and quantities of grooves

1.3 粗糙度对接触面变形特性的影响

接触面的变形特性主要表现为冻土与接触面间滑动产生的相对位移和结构咬合作用下在冻土体内部发生的剪切错动两部分变形[7]。

在冻黏土-结构接触面单剪试验中，不同冻土厚度内，随冻土厚度的增大，冻土颗粒的剪切位移相应地发生了减小，其剪切位移曲线在某一厚度均出现了拐点，此拐点厚度为接触面层厚度[7]。接触面层厚度与接触面的粗糙度之间存在联系，接触面的粗糙度越大，对应的接触面层厚度也越大。但随着粗糙度的持续增大，接触面层厚度的增幅会逐渐减小。通过微变形图像测量技术测得的接触面层厚度随粗糙度变化规律如图4所示(粗糙度定义法见文献[7])。粗糙度在小于界限值时对接触面层厚度起到决定作用，超过界限值时，冻土本身的力学性质决定了接触面层厚度的大小。而在同一冻土厚度内，随着结构接触面粗糙度不断的增大，接触面上土颗粒位移随之发生不同程度的增大，粗糙度对其影响较为显著。

图4 界面层厚度随粗糙度变化关系[7]Fig.4 Relations between thickness of interface layers and roughness

2 考虑粗糙度的接触面剪切本构模型

2.1 Gompertz模型对冻土-结构接触面的适用性

国内外已有很多学者对常温条件下土-结构接触面的本构关系进行过研究。Clough等建立了基于广义Hooke定律的双曲线弹性模型，并得到广泛运用[28]。Brandt建立了屈服强度位于弹塑性分界点的理想弹塑性模型[29]。彭凯等建立了基于广义位势理论的考虑剪胀及应变软化的接触面弹塑性本构模型[30]。胡黎明等建立了基于损伤力学基本原理的接触面本构模型[1]。陈良致等依据冻结青藏粉土-玻璃钢直剪试验中应力-应变曲线特征，建立了冻土接触面应力-位移-温度本构方程[31]。潘一鸣建立了基于能量守恒原则和塑性假设的考虑粗糙度、含水率和土体种类的塑性破坏模型[10]。何菲在分析接触面细观机理的基础上，建立了考虑接触面硬化和弱化效应的黏弹塑性本构模型[32]。夏红春建立了基于应变梯度塑性理论的接触面本构模型[33]。杨林德等建立了考虑接触面内部缺陷分布随机性的统计损伤本构模型[34]。杨平等建立了基于损伤力学理论的冻土-结构接触面剪切行为损伤模型[35]。

研究Gompertz模型对接触面剪应力-剪切位移第一阶段的适用性，并建立考虑粗糙度影响的剪应力-剪切位移表达式，文献[18]中冻结粉土与钢板接触面的剪应力-剪切位移曲线数据(粗糙度值为基于“扩面度”的改进粗糙度算法，无量纲)显示：在剪切初始阶段、位移小于0.3 mm时，由于在负温环境下接触面间“冰膜”的润滑作用，以及不同粗糙度的影响，致使剪切应力增长速率相对缓慢。剪应力-剪位移曲线在接触面达到峰值应力前呈“S”型趋势。

Gompertz模型是一种生长曲线模型，该模型由发生、发展、成熟三个阶段构成，且每阶段速率不同，这与冻结粉土-钢板接触面的剪切力学特征相似。文献[36]介绍了采用Gompertz模型探究粗糙度-剪切应力-位移关系，并对模型预测效果进行评价。

Gompertz模型的数学表达式为：

τ=aexp[-bexp(-cδ)]

(1)

式中：τ、δ分别为剪应力和剪切位移；a、b、c分别为Gompertz模型的相关参数，其中a为曲线极值，b为曲线的变化速率和陡峭程度。

利用Origin对试验数据进行处理，求得Gompertz模型的三个参数a、b、c，其结果见表2。

表2 Gompertz三参数本构模型参数Table 2 Parameters for the constitutive model of roughness, stress， and displacement

采用决定系数R2评价非线性的应力-位移曲线还存在着一定的局限和不足之处，故引入相关因子β[28]来充当评价拟合优劣的标准，其定义为：

(2)

式中：δ(i)为预测位移值；δi为观测位移值；n为样本容量。

关于β的评价指标值如表3所示。

表3 模型拟合相关因子评价标准Table 3 Evaluation standards for the correlation factor β

该试验数据与模型拟合评价结果如表4所示，曲线拟合结果相关因子β的评价结果为优秀和良好，说明利用Gompertz生长曲线模型表达冻结粉土-钢板接触面的直剪试验曲线峰值应力之前阶段是较为合理的。

表4 拟合效果评价Table 4 Evaluations for the simulation effects

2.2 接触面粗糙度-剪应力-剪切位移关系模型

根据文献[15]试验数据拟合结果，以及多组数据与粗糙度之间的关系，得到Ri-τ关系曲线，得出剪应力τ与粗糙度Ri满足：

τ=jlnRi+kRi>0

(3)

式中：τ为剪切应力；j、k的值都是关于位移δ的函数；Ri为粗糙度。

j、k可由式(4)计算：

k=lexp[-mexp(-nδ)]

(4a)

j=a0+a1δ+a2δ2+a3δ3+a4δ4+

a5δ5+a6δ6+a7δ7+a8δ8+a9δ9

(4b)

式中：l、m、n、a0～a9为参数。

式(3)、(4)中各个参数如表5所示，试验数据拟合评价如表6所示。拟合曲线和试验曲线如图5所示。

表5 粗糙度影响下剪应力和位移本构方程各项参数值Table 5 Parameters for the constitutive equation between shear stress and displacement considering of roughness

表6 粗糙度影响下剪应力与位移关系模型参数拟合评价Table 6 Parameter fitting evaluations for the relation model between shear stress and displacement considering the influence of roughness

a—法向应力100 kPa； b—法向应力200 kPa。 Ri=1.404散点坐标； Ri=1.286散点坐标； Ri=1.034散点坐标； ——拟合线。图5 不同法向应力粗糙度下剪应力-剪切位移拟合曲线Fig.5 Fitted curves between shear displacement and sheer stress under different roughness and normal stress

根据拟合推导出的不同粗糙度应力-剪切位移曲线，可以看出：在不同的法向应力下，同一剪切位移所对应的应力值，在接近峰值应力阶段都伴随粗糙度的增大而升高，增幅较前一较小粗糙度相应曲线明显减小。同一剪应力所对应的位移值，粗糙度较大的情况下，产生的位移反而较小。较大粗糙度接触面发生剪切破坏时对应的剪切位移也越大(图5)。

3 粗糙度对接触面剪切特性影响机理

冰晶的冻结力、土体颗粒间、土颗粒与结构摩擦力等共同组成了接触面冻结强度[37]，微观示意如图6所示。在剪切过程中，随着相对剪切位移的不断增大，冰晶的冻结力被破坏。在相对剪切位移不断增大的过程中，黏聚力并不会消失，且其与摩擦力两者共同组成了残余强度稳定发展阶段的残余抗剪强度。

a—光滑接触面； b—粗糙接触面。图6 不同冻土-结构接触面微观示意Fig.6 Schematic diagrams for contact interfaces between different frozen soil and micro structure

对于粗糙度增大导致峰值强度随即增大的现象，其机理为：粗糙度增大后，其接触面结构如图6b所示，冻土与结构间冻结面积增大，并且粗糙度增加导致结构与土中部分剪切面变为大颗粒土的结构剪切面，使峰值强度也随之变大[7]。

在不同冻土厚度内，与结构一起相互约束的界面层厚度也会随着接触面剪应力的增大而变厚，但是粗糙度达到一定的界限值时，即使土体与结构接触表面积增大，剪应力也不会继续增大，其原因是接触面的强度已经达到并大于冻土本身的抗剪强度，在冻土的内部发生了剪切，而非接触面层之间，此时其强度不再受粗糙度的影响。在同一冻土厚度内，土颗粒的位移随接触面粗糙度的增大而增大是因为结构与冻土的接触面积随着粗糙度的增大而增大，较大的接触面积和咬合程度带动接触面土体的范围越大、厚度越厚。

4 粗糙度在实际工程中的应用

由于大批冻土工程构筑物和建筑物相继在寒区修建和使用，其基础与天然冻土间存在着大量的接触问题。如多年冻土地区的桩土之间、寒区隧道衬砌与围岩的接触区域等；同样在非寒区地带，人工冻结加固法的施工过程中，也会出现一系列结构和冻土的接触面问题。如在隧道盾构施工中，盾构机刀盘与其接触的待掘进区域土体之间、施工结束后形成的结构物与土体相接处均存在着大量的接触面问题。该问题广泛存在于各类工程之中，是研究冻土与结构之间力学、变形等特性的重要纽带。冻土-结构接触面剪切特性的研究目的和任务，是通过现场及模型试验或者数值模拟的方法，探究其力学机理及本构关系，最终更好地服务于工程实际，为工程提供有效且准确的理论指导。

冻土和结构接触面粗糙度的增大，会对结构面层抗剪强度的提高起到正向促进作用。在伊卡卢伊特西北地区，Biggar等通过抗拔试验[38-39]测得，焊接有“把柄”的桩的承载力明显增高，是同条件下“光滑”桩承载力的2倍。喷砂桩的承载力更是显著增加，是同样条件下“光滑”桩承载力的4倍。使用“砂性”回填浆液其承载力甚至能够达到平滑桩的8～10倍[40]。“光滑”表面桩呈脆性破坏[40]，在破坏过程中，接触面的强度会毫无征兆的突变至其残余强度，为了避免这种突变的现象，可以将桩侧处理的粗糙一点或者创造波纹系统来达到这一目的。波纹桩可以有效地抑制这种突变，在防止这一现象的过程中展现出了显著的优越性[40]。由此可见，在桩基工程中，改变结构接触面的粗糙度，可以极大地提高桩体的承载力，明显地抑制桩土之间的脆性破坏。

对于结构界面粗糙度来说，并非越大对工程越有利，相反，较小或“光滑”的界面也会给工程带来较大的益处。利用光滑玻璃钢等粗糙度较小的接触面在基础之上，可以有效地削减多年冻土和基础接触面间的冻结作用，从而达到减小切向冻胀力的作用。温智等通过青藏粉土-玻璃钢接触面直剪试验验证并成功在青藏直流输变电工程之中实际应用，减小了冻胀力对基础的冻拔作用[41]。

5 结束语

1)冻土-结构接触面剪应力-剪切位移曲线存在明显的峰值，破坏后应力下降较为明显，之后，应力-位移曲线趋于平缓，接触面峰值强度值与粗糙度相关性较大，残余强度受粗糙度的影响不大。同一冻土厚度上，粗糙度越大，冻土颗粒的相对位移亦愈大，因为粗糙度增大，凹槽对土颗粒的带动会随之增大。同样，粗糙度增大，剪胀性愈发显著。

2)Gompertz模型能较好地模拟峰值强度之前冻结粉土-钢板剪应力-剪切位移曲线，建立的考虑粗糙度影响的冻结粉土与钢板接触面剪应力-剪切位移关系模型能较准确预测不同粗糙度下冻土-钢板接触面剪应力-剪切位移曲线。但还无法寻找出粗糙度的最优情况，在此方面还需进一步改进。

3)冰晶的冻结力、土体颗粒间、土颗粒与结构摩擦力等共同组成了接触面冻结强度。粗糙度的增大会改变剪切面面积，并改变土颗粒在结构接触面中的排列以及镶嵌方式，从而提高剪切强度。粗糙度对接触面抗剪强度的影响体现在粗糙度对黏聚力及内摩擦角的共同影响。

4)当前的研究中，对粗糙度的定义还不够统一，没有建立统一的粗糙度度量标准。在粗糙度的定义量化上，每种方法都具有一定的局限性，且各种方法之间的相互转化较为困难，亟需建立粗糙度量化标准。