型钢混凝土异形柱空间框架地震反应分析模型简化方法研究*

毛冬旭 刘祖强 薛建阳 张风亮 陈力莹

(1.陕西省建筑科学研究院有限公司， 西安 710082； 2.西安建筑科技大学土木工程学院， 西安 710055；3.陕西建科建设特种工程有限公司， 西安 710082)

目前国内外对型钢混凝土异形柱框架的地震反应分析[1-3]多采用平面模型为主，其主要原因除了结构多维理论的发展进程缓慢、课题研究经费成本受限等以外，力学单元模型难以充分模拟框架柱的双向压弯耦合是问题的关键[4-5]。虽然采用纤维模型的研究方法可以较为真实地模拟型钢混凝土异形柱空间框架在地震作用下的非线性动力响应，但也仅适应于空间框架模型杆件数量不太多的情况。

考虑到结构沿某主轴方向的抗侧力构件承担该方向的地震作用，平面模型的分析方法一般先从空间框架跨数较多的纵向中间选取一榀框架模型作为研究对象，然后将平面模型的分析结果应用到空间框架的地震反应分析中。然而，型钢混凝土异形柱框架的角柱、边柱和中柱的截面形式不同，具有较强的空间性，因此简化为平面模型能否较好地反映三维整体结构的真实地震反应，将直接影响研究成果应用到实际工程的效果。

若直接将空间框架的地震反应与相应的平面框架进行对比，则其结论显然无法真实反映传统平面框架提取方法存在的误差。本文以1个规则的3榀2跨8层的型钢混凝土异形柱空间框架为分析模型，为了更好地研究该结构地震反应分析时空间框架转换为平面框架的方法，以双向地震作用下的空间模型(SF2)、单向地震作用下的空间模型(SF1)、调整后的平面模型(PF1)三者为研究对象，其中将单向地震作用下的空间模型作为平面模型和双向地震作用下空间模型之间的对比桥梁，分别考察三者在地震作用下的动力响应，进而评估型钢混凝土异形柱空间框架简化为平面模型进行地震反应分析的合理性。

1 模型概况

1.1 型钢混凝土异形柱空间框架模型

依据JGJ 149—2017《混凝土异形柱结构技术规程》和JGJ 138—2016《组合结构设计规范》，本文设计了1个双向2跨8层的型钢混凝土异形柱空间框架。

空间框架模型标准层平面尺寸为8.48 m×8.48 m，首层层高为3.6 m，2～8层层高为3.0 m，因此试验模型总高度为24.6 m，空间框架模型的剖面示意如图1所示，标准层平面示意如图2所示。设计空间框架模型时，设防烈度为8度，基本地震加速度为0.2g，Ⅱ类场地，设计地震分组为第二组，特征周期Tg=0.4 s。空间框架模型中型钢混凝土异形柱、钢筋混凝土梁和板的几何尺寸及配钢(筋)形式如图3所示。

图1 空间框架剖面示意 mmFig.1 Profile of the spatial frame

图2 空间框架标准层平面 mmFig.2 Standard floor plan of the spatial frame

a—楼板配筋； b—异形柱的几何尺寸及配钢(筋)； c—框架梁截面配筋。图3 构件几何尺寸及配钢(筋) mmFig.3 Component geometric sizes and reinforcement

1.2 型钢混凝土异形柱平面框架模型

型钢混凝土异形柱平面框架从上述空间框架中提取，提取方法与传统方法有所不同。首先沿X向取出中间榀框架作为分析模型，然后为考虑边框架的影响，对所取平面框架的周期进行调整，使其周期与空间框架在该方向的周期相等，此操作实际上是通过调整该平面框架的从属面积宽度来实现的，按照支撑双向板的梁，从属面积由板面的剪力零线围成，从每一区格板四角处作45°角线与平行于长边的中线相交，将整片板分为4个板块，每个板块上的荷载传递给相邻支承梁，即从图4中的4 000 mm调整为3 237 mm[6]。这一提取方法本质是通过调整平面框架的从属面积宽度达到减小其重力荷载代表值(即振动质量)的目的，而框架刚度(或梁柱截面尺寸)保持不变，从而实现了对平面框架基本周期的调整。这种调整不仅改变了竖向荷载，更重要的是平面框架分担的水平地震惯性力也相应减小。研究表明[7]，用这样的方法近似考虑边榀框架的影响是可行的。

图4 质量修正平面框架示意 mmFig.4 The schematic diagram of the quality corrected plane frame

2 模型建立及分析方法

2.1 有限元模型的建立

采用OpenSees Navigator有限元软件建立SRC异形柱框架结构的有限元模型，对于该有限元模型的材料本构关系、单元选取、截面定义、结构质量矩阵和阻尼矩阵的确定如下所示。

该有限元模型的混凝土本构模型选用OpenSees Navigator软件中的Concrete01 Material，混凝土受压时的骨架曲线为经过Scott等修正后的Kent-Scott-Park模型[8]。型钢和钢筋的本构模型均采用Steel02 Material，是由Menegotto和Pinto最先提出，并经过Filippou等修正后能够考虑等向应变硬化的本构模型[9]。该模型采用显函数的应变表达方式，从而反映出Bauschinger(包辛格)效应，提高模型的计算效率。

材料的本构模型是非线性的，故采用OpenSees Navigator有限元软件建模时需要选取合适的非线性分析单元模型。选取基于力的梁柱杆系单元(Force-Based Beam-Column Element)来模拟框架结构。基于纤维模型将纤维截面赋予框架结构的构件截面，分析时先计算各纤维截面上的抗力和刚度矩阵，再通过Newmark积分法沿杆长变化求解出整个单元模型的切线刚度矩阵和截面抗力[10]。模型中积分点的选取多少能够体现构件截面柔度的精度拟合程度，同时也要考虑模型的计算效率，一般选取3～6个积分点即可满足精度要求，综合计算效率和模拟精度的要求，本文取5个积分点。

在完成整个模型结构的动力时程分析前，可以通过结构离散化的方法来转换其结构动力自由度，从而可以简化其有限元程序的计算过程。动力分析时施加在结构上的恒、活载值是重力荷载代表值，即活荷载是考虑了组合系数以后再施加上去的。由于分析模型中没有对楼板进行建模，因此重力荷载是按照传力途径将板荷和次梁荷载以线荷载和集中荷载的方式直接施加在主梁上。该有限元模型选用集中质量法来确定质量矩阵，首先需要将施加在楼板承担的恒载和活载按照板的传力方式分配给框架梁，然后将框架梁承担的荷载均匀分配到节点上，最后由集中质量法换算相应的节点质量(只考虑平动质量，忽略转动惯量的影响)，其间通过静力凝聚的方式可以减少结构动力自由度数量，提高分析计算的效率。

结构的阻尼一般很难用实际测量方法来获得，而Rayleigh阻尼模型满足振型正交条件，应用方便、快捷，在结构动力分析计算中被广泛采用。Rayleigh阻尼定义的参数设置如图5所示。

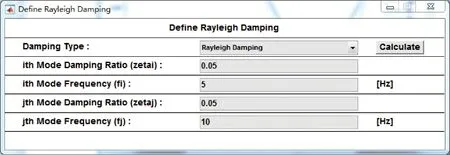
图5 OpenSees Navigator阻尼定义Fig.5 OpenSees Navigator damping definition

2.2 地震波及加载工况的选取

根据Ⅱ类场地特点，按照GB 50011—2010《建筑抗震设计规范》(2016版)的相关规定选取El Centro波、Taft波和Lanzhou波作为加载地震波，3种地震波的相关设置参数如表1所示。

表1 原始地震波的参数设置Table 1 Parameter settings of the original seismic wave

在综合动力分析和研究目的的基础上选取表2所示的加载工况作为SF2地震波输入工况，SF1和PF1地震波输入工况参考表2所示的X向地震波依次进行。

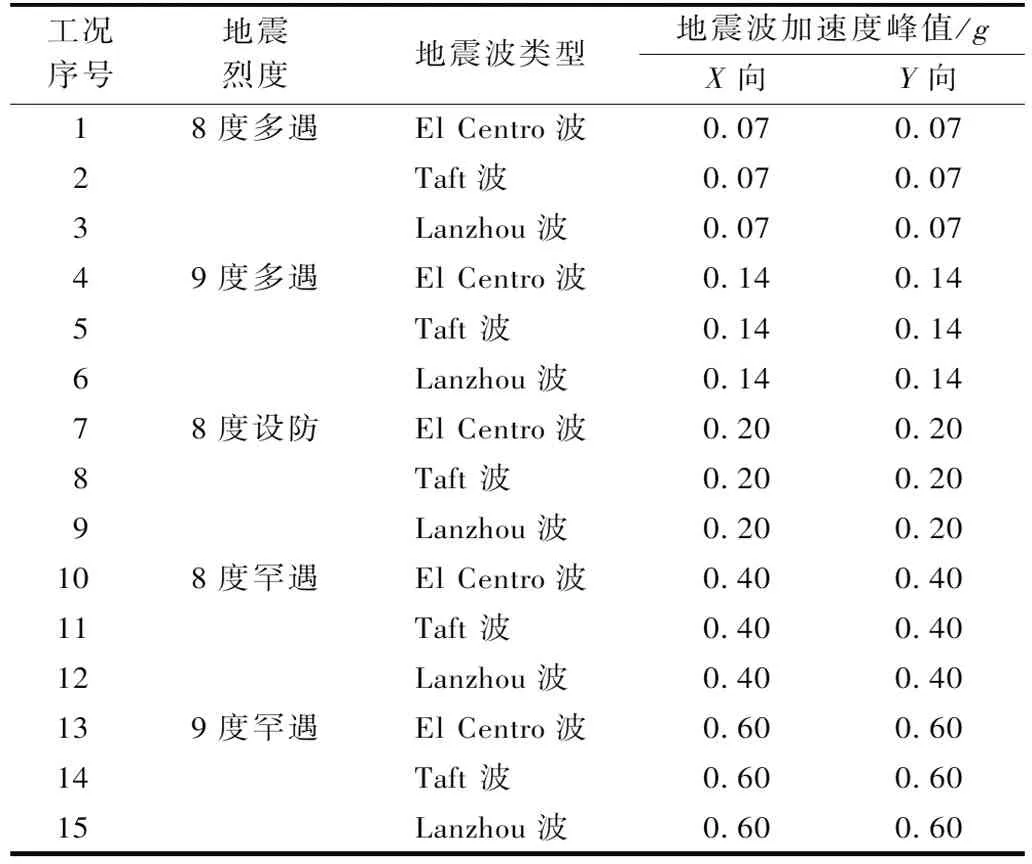
表2 各烈度双向地震波输入工况Table 2 Bi-directional seismic wave input conditions of various intensities

3 非线性地震反应分析结果及评价

3.1 加速度反应对比分析

对OpenSees Navigator有限元软件模拟得到的加速度时程曲线进行对比分析。限于篇幅，图6～8所示为SF2、SF1和PF1对应3种地震波部分工况的顶层加速度反应时程曲线对比结果。

a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图6 El Centro波顶层加速度反应时程对比曲线Fig.6 Comparisons of time-history curves of acceleration response at the top floor under El Centro wave

a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图7 Taft波顶层加速度反应时程对比曲线Fig.7 Comparisons of time-history curves of acceleration response at the top floor under Taft wave

a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图8 Lanzhou波顶层加速度反应时程对比曲线Fig.8 Comparisons of time-history curves of acceleration response at the top floor under Lanzhou wave

由图6～8可知，在相同烈度的地震作用下，SF2、SF1和PF1三者间有相似的振动规律，在整体反应过程中变化趋势基本吻合，加速度反应基本一致，加速度峰值出现的时间较为相近。从加速度反应时程曲线可以看出，模型结构在El Centro波地震作用下的振动反应较Taft波和兰州波更为显著，因而将三者在El Centro波对应不同烈度下的最大加速度值对比结果列于表3。由表3的对比结果可知，三者在El Centro波作用下的各层最大加速度反应值对比结果差值均在10%以内，SF2和SF1对比最大差值为9.1%；SF2和PF1对比最大差值为7.1%；SF1和PF1对比最大差值为6.7%，故从最大加速度反应值对比结果来看，三者的振动反应较为相似，误差较小。从加速度反应对比结果可知，将传统型钢混凝土异形柱平面框架分析模型经过质量调整后替代型钢混凝土异形柱空间框架进行地震反应分析是可行的。

表3 El Centro 波在不同烈度地震作用下各层最大加速度值对比Table 3 Comparisons of maximum acceleration values of El Centro waves under the earthquake action of different intensities g

3.2 位移反应对比分析

图9～11所示为SF2、SF1和PF1对应3种地震波部分工况的顶层位移反应时程曲线的对比结果。由图9～11可知，在相同烈度地震作用下，SF2、SF1和PF1有相似的位移反应规律，尽管PF1的顶层位移反应稍有不同，但从整体反应来看，三者的变化趋势基本吻合，位移反应峰值出现的时间较为相近。

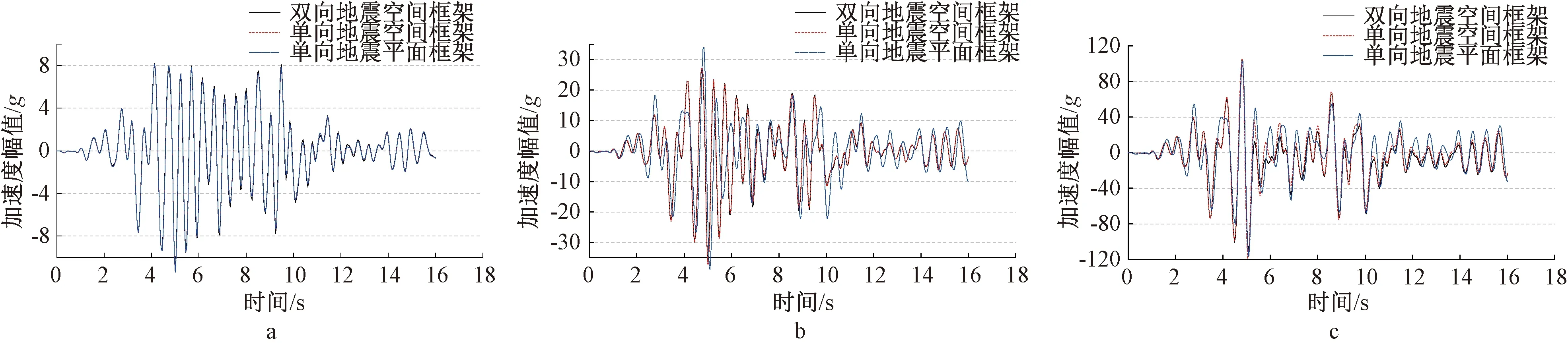
a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图9 El Centro波顶层位移反应时程对比曲线Fig.9 Comparisons of displacement response time-history curves of the top floor under El Centro wave

a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图10 Taft波顶层位移反应时程对比曲线Fig.10 Comparisons of displacement response time-history curves of the top floor under the Taft wave

a—8度多遇(0.07g)地震阶段； b—8度设防(0.20g)地震阶段； c—9度罕遇(0.60g)地震阶段。图11 Lanzhou波顶层位移反应时程对比曲线Fig.11 Comparisons of displacement response time-history curves of the top floor under Lanzhou wave

从顶层位移反应时程曲线可以看出，模型结构在El Centro波作用下的位移反应较Taft波和兰州波更为强烈，将El Centro波作用下各层最大位移和层间位移角对比结果分别列入表4和表5。由表4的最大位移反应值对比结果可知，三者间的各层最大位移反应值对比结果差值均保持在10%以内，SF2和SF1对比最大差值为7.4%；SF2和PF1对比最大差值为8.9%；SF2和PF1对比最大差值为6.7%，由此可以看出，三者的位移反应较为相似，误差较小。由表5的层间位移角对比结果可知，SF2、SF1和PF1三者各层的层间位移角较为接近(7、8层的层间位移角看似存在一定差异，但由于这两层的层间位移角很小，实际差值也很小)，较易发生弹塑性变形的底部各层结果相近，说明三者在地震作用下的层间变形较为接近。

表4 El Centro 波在不同烈度地震作用下各层最大位移值对比Table 4 Comparisons of maximum displacement values of various layers of El Centro waves under earthquakes of different intensities mm

表5 El Centro 波在不同烈度地震作用下层间位移角对比Table 5 Comparisons of displacement angles between layers of El Centro waves under earthquakes of different intensities

综合顶层最大位移反应和各层层间位移角的对比结果可知，将型钢混凝土异形柱空间框架采用经过质量调整后的型钢混凝土异形柱平面框架替代后进行地震反应分析是可行的。

3.3 基底剪力-顶层位移滞回曲线对比分析

图12～14所示为SF2、SF1和PF1对应3种地震波部分工况的基底剪力-顶层位移滞回曲线。由图12～14可知，8度设防(输入峰值加速度为0.20g)地震作用下的滞回曲线呈狭长状，包围的面积小，表明结构底层处于刚刚屈服或即将进入屈服的状态；9度罕遇(输入峰值加速度为0.60g)地震作用下滞回曲线已经明显向位移轴倾斜，包围的面积较大，表明结构已经进入塑性状态。将滞回曲线进行对比可知，三者在不同烈度地震波作用下的滞回曲线基本类似，且最大基底剪力对应的位移相近。因此，由基底剪力-顶层位移滞回曲线对比结果可知，将型钢混凝土异形柱平面框架分析模型经过质量调整后替代型钢混凝土异形柱空间框架进行地震反应分析是可行的。

a—0.20g双向地震空间框架； b—0.60g双向地震空间框架； c—0.20g单向地震空间框架； d—0.60g单向地震空间框架； e—0.20g单向地震平面框架； f—0.60g单向地震平面框架。图13 Taft波地震作用下基底剪力-顶层位移滞回曲线Fig.13 Hysteretic curves of basement shear force and top floor displacement under Taft wave

a—0.20g双向地震空间框架； b—0.60g双向地震空间框架； c—0.20g单向地震空间框架； d—0.60g单向地震空间框架； e—0.20g单向地震平面框架； f—0.60g单向地震平面框架。图14 Lanzhou波地震作用下基底剪力-顶层位移滞回曲线Fig.14 Hysteretic curves of basement shear force and top floor displacement under Lanzhou wave

3.4 滞回耗能分析

根据位移反应时程曲线和恢复力时程曲线可以得到SF2、SF1和PF1对应不同烈度的瞬时耗能时程曲线，如图15所示。三者的累积耗能时程曲线可根据式(1)[11]的计算得到，结果如图16所示。

a—8度多遇(0.07g)El Centro波； b—8度设防(0.20g)El Centro波； c—9度罕遇(0.60g)El Centro波； d—8度多遇(0.07g)Taft波； e—8度设防(0.20g)Taft波； f—9度罕遇(0.60g)Taft波； g—8度多遇(0.07g)Taft波； h—8度设防(0.20g)Taft波； i—9度罕遇(0.60g)Taft波。图15 各地震波在不同烈度地震作用下瞬时耗能对比Fig.15 Comparisons of instantaneous energy consumption of seismic waves under earthquakes of different intensities

a—8度多遇(0.07g)El Centro波； b—8度设防(0.20g)El Centro波； c—9度罕遇(0.60g)El Centro波； d—8度多遇(0.07g)Taft波； e—8度设防(0.20g)Taft波； f—9度罕遇(0.60g)Taft波； g—8度多遇(0.07g)Taft波； h—8度设防(0.20g)Taft波； i—9度罕遇(0.60g)Taft波。图16 各地震波在不同烈度地震作用下累积耗能对比Fig.16 Comparison of total cumulative energy consumption of various seismic waves under earthquakes of different intensities

(1)

式中：Fi+1、Fi分别表示第i+1和第i点的结构恢复力值；Xi+1、Xi分别表示第i+1和第i点的位移反应值。

由图15可知，SF2、SF1和PF1的瞬时耗能能力随着地震烈度的增加呈递增趋势，三者在El Centro波作用下瞬时耗能时程曲线的耗能峰值出现时刻较为吻合，Taft波和Lanzhou波作用下的耗能峰值出现时间有所出入，平面框架呈现出滞后现象，但滞后时间在5 s以内，且三者瞬时耗能时程曲线的耗能峰值大小基本相同。由图16可以看出，随着地震烈度的增加，框架的累积耗能逐渐增大，在8度多遇(输入加速度峰值为0.07g)和8度设防(输入加速度峰值为0.20g)地震作用下，结构的累积耗能较小，表型此时尚未进入弹塑性工作状态，滞回耗能以弹性应变能为主，在9度罕遇(输入加速度峰值为0.60g)地震作用下，结构进入弹塑性状态，耗能以塑性应变能为主，总累积耗能增幅较为明显；三者的累积耗能时程曲线变化趋势较为吻合，且总累积耗能也较为相近。综合瞬时耗能和总累积耗能的对比结果，认为可将空间框架简化成质量调整后的平面框架进行地震反应分析。

4 结束语

1)为了将型钢混凝土异形柱空间框架简化为平面框架进行地震反应分析，可通过调整从属面积宽度减小平面框架重力荷载代表值，保证空间框架与平面框架之间的刚度或梁柱截面尺寸不变，将平面框架所分担的水平地震惯性力相应减小，从而实现了对平面框架基本周期的调整，完善了传统简化方法的不足。

2)由加速度反应和位移反应时程曲线可以看出，SF2、SF1和PF1有相似的振动规律，整体动力响应变化趋势基本吻合，加速度、位移峰值出现的时间较为相近；层间位移角除7～8层的差异比稍大外，易发生弹塑性变形的底部各层结果接近。

3)SF2、SF1和PF1在未屈服和屈服状态下的滞回曲线相似度较高，且最大基底剪力值趋于相同。结构在不同地震波作用下的瞬时耗能随着地震烈度的增加呈递增趋势，SF2、SF1和PF1的瞬时耗能峰值大小基本相同，累积耗能时程曲线变化趋势较为吻合，且总累积耗能较为相近。

4)综合SF2、SF1和PF1在El Centro波、Taft波和Lanzhou波作用下的加速度反应、位移反应、基底剪力-顶层位移滞回曲线、瞬时耗能和累积耗能时程曲线对比结果，采用经过质量调整后的型钢混凝土异形柱平面框架模型替代型钢混凝土异形柱空间框架进行地震反应分析是可行的。