砂岩注水储层细菌堵塞时空演化定量模拟技术

蒋官澄，孙 喆，盛科鸣，董腾飞，朱鸿昊，贺垠博, 张耀元

(1.中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249； 2.中国石油大学(北京)石油工程教育部重点实验室，北京 102249； 3.中国石油大学(北京)石油工程学院，北京 102249； 4.卡尔加里大学化学与石油工程学院，卡尔加里 T3S;5.中国石油大学(北京)人工智能学院，北京 102249; 6.中海油能源发展股份有限公司工程技术分公司,广东湛江 524057)

注水开发是油田最主要开发方式。注入水中通常含有不同种类和数量的细菌以及各类细菌营养源，若营养源、pH值、温度以及矿化度等条件适宜细菌生长，细菌将在储层中大量繁殖生成细菌群落，从而造成严重储层损害[1-4]。例如，硫酸盐还原菌的阴极去极化作用会产生硫化氢，降低流体pH值、腐蚀注水管网，还可通过代谢作用产生硫离子并与腐蚀产物结合生成不溶沉淀，堵塞注水管道与储层孔隙；腐生菌代谢后产生黏稠状物质，易黏着于储层孔隙，降低储层渗流能力。数据显示，细菌造成的储层损害最高可使储层渗透率减小90%以上[5-6]。注入水中细菌堵塞损害储层问题的研究方法主要分为两种：一为实验法，虽具有直观性但工作量大，且室内实验条件常难以模拟真实储层状况，导致实验结果的误差较大；二为数值模拟法[7-16]，即利用基础数据，结合物理、化学、生物理论描述细菌堵塞损害储层机，建立数值模型并进行模拟计算。数值模拟法虽直观性较差，但能模拟复杂过程并能快速得到结果，更适用于研究细菌堵塞损害储层问题。Yavuz等[17]推导出细菌多孔介质单向流运移的控制方程；Sivasankar等[18]考虑了温度、pH值对细菌繁殖的影响，并在控制方程中引入了多相流、多细菌元条件；Khan等[19]建立了可模拟地层营养物消耗以及细菌繁殖的非均质模型；Hosseininoosheri等[20]考虑温度、矿化度等因素，利用UTCHEM(化学驱数值模拟器)方法建立了细菌渗流模型；Islam[21]结合细菌繁殖动力模型建立了能够模拟细菌堵塞的多维孔隙介质模型。细菌堵塞储层是细菌在储层环境下(岩石物性、矿化度、pH值、温度、压力等)运移、吸附、沉积、代谢以及营养物在储层环境下运移、吸附、沉积、消耗等多因素共同制约的结果[10, 17-18,22-27]。考虑到高度耦合、高非线性度方程不适用于描述矿场尺度(井筒中心向储层延伸约数米的空间区域)以及待模拟井的某些影响因素相对恒定。笔者以影响细菌堵塞储层的主要因素为变量，基于多孔介质传质、传热理论，建立适合现场应用且可操作性强的矿场尺度下砂岩储层细菌堵塞数值模型，并进行数值求解，实现对细菌堵塞储层的时空演化定量模拟。

1 砂岩储层细菌堵塞时空演化数值模型的建立

以中国普遍存在的、具渗透率各向异性的砂岩注水储层为研究对象，并假设：①注水层段中流体为二维、水平流动，无层间干扰；②注水层段中pH值、矿化度、压力梯度、迂曲度等恒定；③细菌在储层油、水相中均匀分布。由于对特定待模拟井这些因素对模拟的宏观结果影响不大，假设合理。细菌及营养物的物化作用示意图如图1所示。

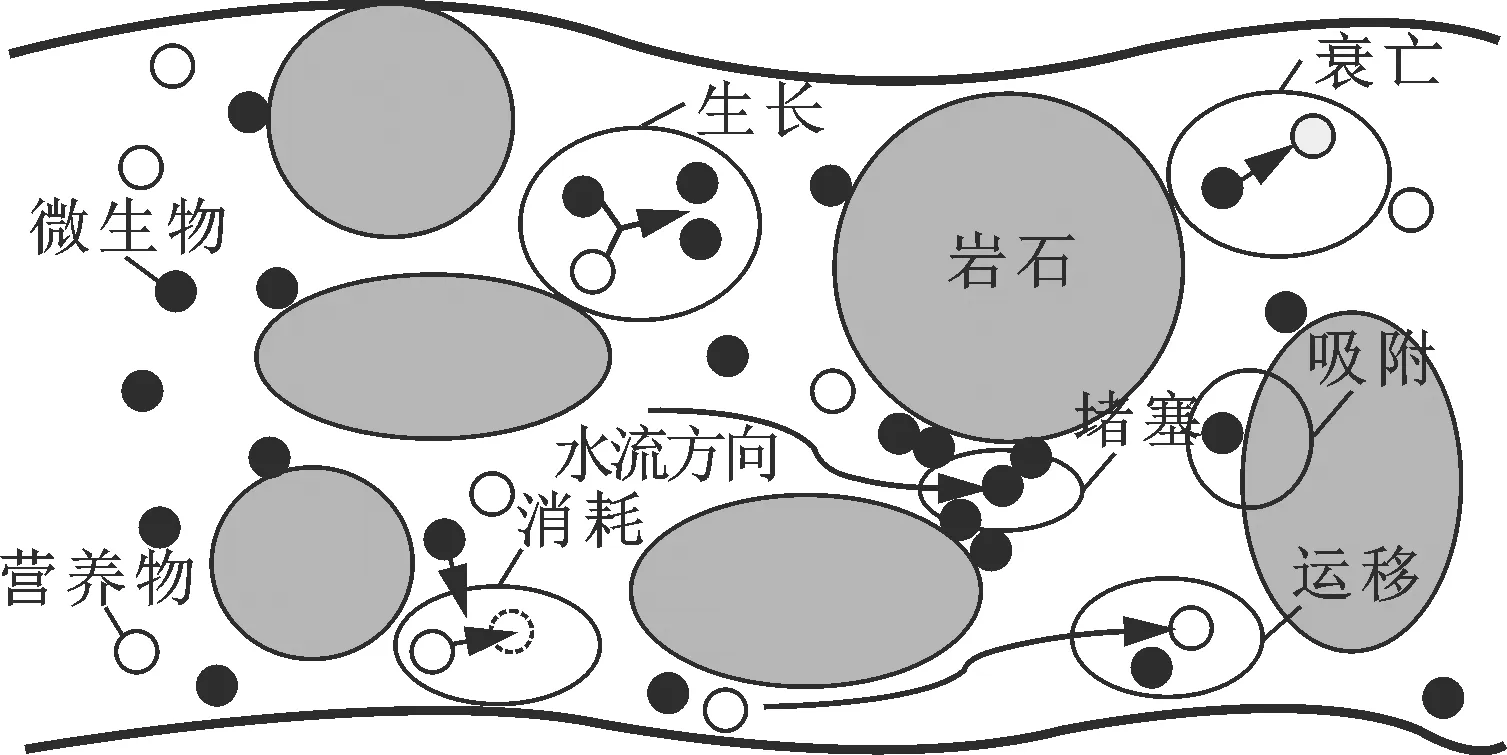
图1 细菌及营养物质物化作用示意图Fig.1 Schematic diagram of physicochemical action of bacteria and nutrients

1.1 储层温度分布与细菌最大生长速率模型

细菌代谢由细胞内各种酶的催化作用控制，而酶的活性对温度极为敏感，过高或过低的温度都会使酶失活，且注水会使井内与储层间形成温度变化前沿，也会影响细菌代谢，因此首先进行储层温度分布规律研究。

在注水过程中，由于注入水温度与储层温度间存在温度差，能量在储层岩石与流体中以温度变化的形式传递。运用多孔介质传热理论，根据能量守恒定理建立矿场尺度储层温度分布数学模型，得到储层温度分布控制方程[10]为

(1)

式中，T为温度，℃；t为时间，d；Dconx和Dcony分别为x和y轴方向储层液体导热系数，m2/d；Ddisx和Ddisy分别为x和y轴方向导热率，m；vmeanx和vmeany分别为x和y轴方向注入水流速，m/d。

该模型为经典的定温边界模型，边界条件为

∂T/∂x=0, ∂T/∂y=0.

(2)

储层温度严重影响细菌最大生长速率，进而影响细菌在储层中的分布情况。以前虽建立了变温条件下细菌量的一般模型，以及含有活化能、频率因数等参数的平方根模型来描述细菌最大生长速率[28-33 ]，但两类模型的现场适用性差。在注水水源和细菌营养源充足的约束条件下，本文中采用温度为主变量的细菌最大生长速率经验公式模拟细菌在储层中最大生长速率的空间分布情况[31]，即

gmax=b(T-Tmin)[1-exp(c(T-Tmax))].

(3)

式中，gmax为细菌最大生长速率，d-1；Tmax和Tmin分别为细菌适宜生长的最高和最低温度，℃；b为细菌生长经验参数，℃-1·d-0.5；c为细菌生长经验参数，℃-1。

1.2 细菌堵塞储层时空分布数值模型

细菌自身涉及各种物理、化学以及生物作用，包括浓度梯度产生细菌扩散、注入水产生细菌对流运移、细菌布朗运动、细菌鞭毛振动导致细菌无规则运动、细菌向高浓度营养物质区域定向运动的趋化性作用以及细菌的生长与衰亡。由于细菌鞭毛振动导致的无规则运动在储层中的宏观作用效果不明显，模型中将其合并入对流项；细菌布朗运动作用被细菌扩散作用覆盖；细菌趋化性作用对储层中细菌分布规律影响较小，被对流效果覆盖，将其与对流项合并为一项；细菌生长为不可逆一级反应，细菌衰亡作用由经典Monod方程表示[17]。由于细菌附着于储层岩石上形成生物膜，且细菌与岩石之间存在解吸附过程，根据质量守恒定理，储层中细菌质量浓度分布方程(Cbacteriatran=θCbacteria)[34]为

(4)

其中

式中，Dsumx和Dsumy分别为x轴和y轴方向细菌弥散系数，m2/d；kdecay为衰亡速率常数，d-1；θ为孔隙度，%；Cbacteriatran为储层流体中细菌表观质量浓度，g/L；Cbacteria为储层流体中细菌真实质量浓度，g/L；Cdeposition为细菌在岩石表面附着量，g/L;gactual为细菌实际生长速率，d-1；ks为Monod半生长系数，g/L；Cnu为储层流体中营养物的真实质量浓度，g/L。

影响细菌在岩石表面附着量的主要因素为细菌吸附与解吸附速率，且细菌附着于储层岩石表面会形成生物膜，则岩石表面细菌附着量方程为

Cdeposition=kcloggingCbacteriatran-kdecloggingVbacteriation.

(5)

其中

Vbacteriatran=ρVbacteria.

式中，kclogging为堵塞速率常数，d-1；kdeclogging为解堵速率常数，d-1；Vbacteriation为细菌在岩石表面总量，g；Vbacteria为细菌在岩石表面的总体积，cm3。

营养物在储层中运移的情况与细菌类似，浓度差产生营养物扩散，注入水产生营养物对流。此外，细菌代谢会消耗营养物，该过程仍由Monod生长方程表示。根据质量守恒理论，营养物质量浓度分布方程(Cnutran=θCnu)为

(6)

式中，Dnusumx和Dnusumy分别为x轴和y轴方向营养物弥散系数，m2/d；Y为产率系数，常数；Cnutran为储层流体中营养物的表观质量浓度，g/L。

岩石表面细菌量由细菌生长、衰亡净增值与附着量决定，附着在岩石表面的细菌会形成生物膜降低储层孔隙度，从而根据泊肃叶公式得出渗透率降低比率，其表达式为

(7)

式中，ρ为细菌质量浓度，g/L。

根据高才尼方程，储层的渗透率与储层孔隙度、迂曲度、岩石外表体积为基准的比表面积有关[35]，其表达式为

(8)

式中，k为储层渗透率，10-3μm2；τ为储层迂曲度，常数；sp为岩石外表体积为基准的比表面积，cm2/cm3。

公式(1)、(3)～(8)组成的方程组构成了砂岩注水储层细菌堵塞时空演化定量数值模型。利用该模型可模拟从注水开始某注水井细菌损害储层的空间定量分布规律以及随时间推移的变化情况，从而实现细菌堵塞储层时空演化定量模拟诊断。上述模型综合考虑了储层温度分布对细菌生长的影响，以及细菌运移、营养物运移、细菌附着与代谢等过程，较为全面。

2 数值求解

2.1 数值模型网格划分

数值模型为矿场尺度模型，选取经典的正交网格划分储层，网格步长设为Δx=Δy=0.1 m。

2.2 控制方程数值求解

为增强可视化程度，利用数值模型求解结果以成像图形表示。二维计算每个时间点分别获得一个平面图，多个时间点对应多个平面图，由上到下按照时间序列排布组成层状图，一个时间点对应一个时间层。由于温度分布会影响细菌分布，所以在计算每一个时间层时都需要对细菌、温度等参数重新计算，从而提高数值模型计算结果与实际情况的吻合程度。

从注水开始，细菌随注入水进入储层，并在储层中大量繁殖，形成渗透率的矿场尺度时空分布，其中(x，y)表示储层二维坐标，n表示计算时间层。温度分布计算采用五点隐式差分格式。由于细菌质量浓度、营养物质量浓度以及细菌吸附传质方程高度耦合，中心、向前、向后差分方法都无法确保计算结果准确性，因此计算细菌及营养物分布时采用适用性强的Crank-Nicolson差分格式。数值求解采用储存单元少、效率高、收敛速度快的Gauss-Seidel迭代。通过控制方程能获得不同时期细菌质量浓度、营养物质量浓度、细菌损害储层分布规律，以及不同时期细菌损害储层的时空演化分布，控制方程为

(9)

其中

(10)

其中

(11)

其中

(12)

其中

Av2=Av1kdecloggingΔt.

数值模型计算流程如下：根据初始条件计算下一时刻储层温度空间分布；由温度分布获得细菌最大生长速率；结合细菌最大生长速率求解耦合的细菌、营养物质量浓度控制方程。经反复迭代，若细菌、营养物质量浓度分布计算结果满足收敛条件则将该时间层数值作为初始数值计算下一时间层结果。

3 细菌损害储层时空演化定量模拟

3.1 数值模拟验证

细菌对储层造成的损害是由细菌大量繁殖而成的，即在细菌对储层损害的各因素中细菌质量浓度是核心。本文中的细菌对储层损害时空演化定量模拟技术也是在该原则指导下建立的，因此细菌质量浓度模拟结果的准确性对储层损害时空演化模拟尤为重要。采用Hosssain等[36]在2008年进行的储层条件下细菌质量浓度分布实验测定时的实验参数，根据方程(1)～(7)计算不同储层深度下的细菌质量浓度，将数值模拟结果与Hosssain等的实测结果进行对比，结果如图2所示。由图2可以看出，计算得出的细菌质量浓度曲线与实测值吻合度很高，验证了数值模拟的正确性。

模拟计算参数如下：空间步长为0.1 m,求解空间范围为5 m,时间步长为0.1 d,原始孔隙度为20%；细菌密度为1 g/L,液体平均流速为0.36 m/d,产率系数为0.53,细菌和营养物扩散系数均为0.001 86 m2/d,注入水初始细菌和营养物质量浓度均为40 g/L；Monod半生长系数为100，衰亡、堵塞和解堵速率常数分别为0.086 4、5.616和37.584；注水温度为12 ℃，地层初始温度为60 ℃，储层热扩散系数为0.041 7 m2/s，导热率为5 W/(m·K)，细菌增长最高和最低温度分别为60和45 ℃。

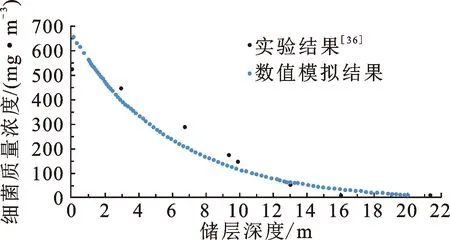
图2 数值模拟结果与实验结果[36]对比Fig.2 Comparison between numerical simulation results and experimental results[36]

3.2 细菌和营养物质量浓度对细菌堵塞储层的影响

注水速度为0.36 m/d，利用上述参数和方程(1)、(3)～(8)计算得到细菌、营养物质量浓度的变化情况，结果如图3～5所示。

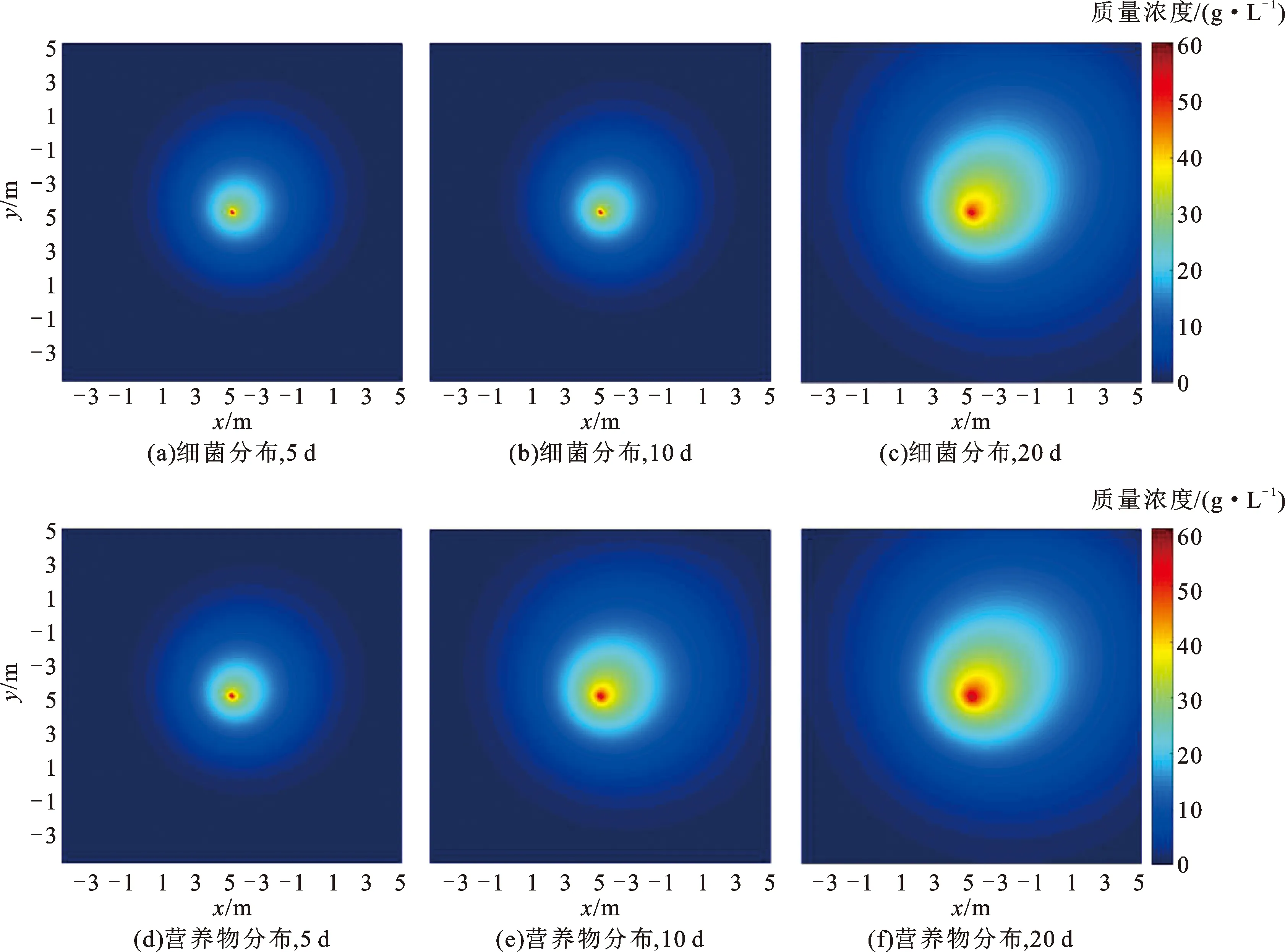
图3 不同注水时间和距离下细菌和营养物质量浓度的时空演化Fig.3 Temporal and spatial evolution of bacterial and nutrient concentration under different water injection time and distance

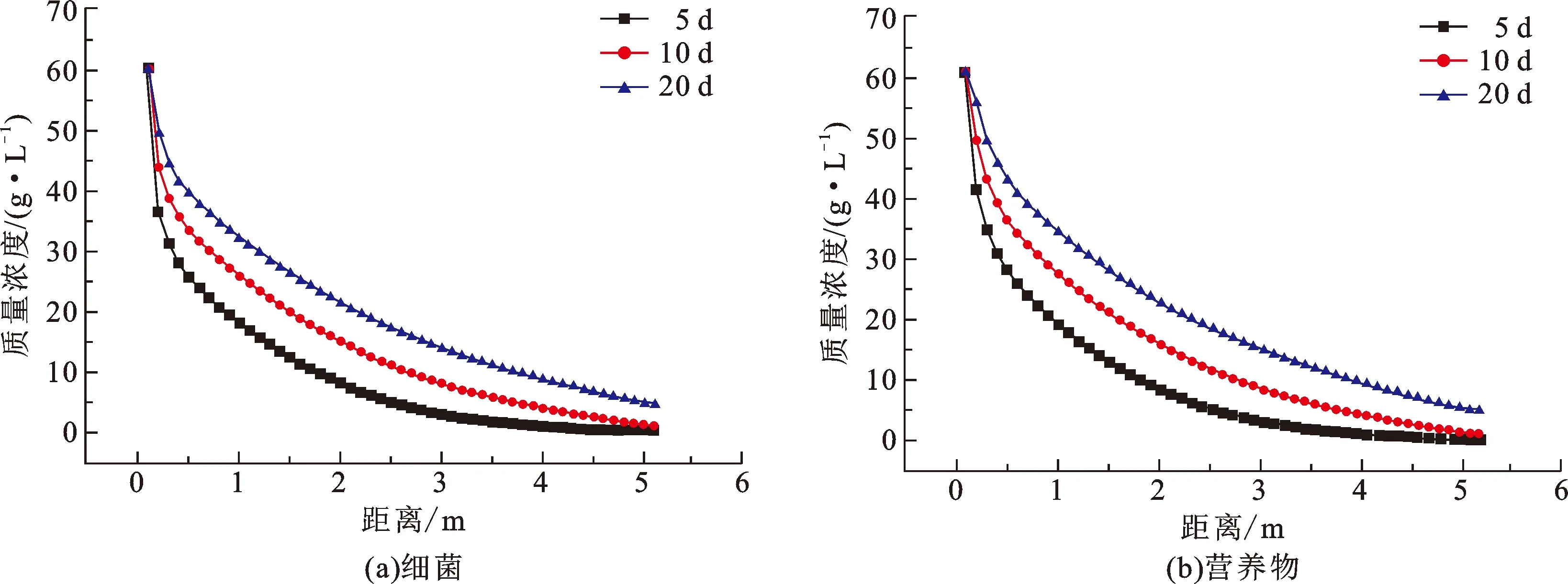
图4 不同注水时间和距离下细菌和营养物质量浓度的变化Fig.4 Variation of bacterial and nutrient concentration under different water injection time and distance

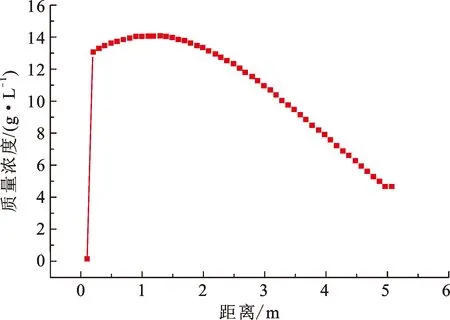
图5 细菌在x轴方向质量浓度从5 d到20 d的增值随井筒中心距离变化Fig.5 Increment of bacteria concentration in x-axis direction from 5 days to 20 days with distance from center of wellbore

从图3、4可知，随着注水时间增加，细菌、营养物质量浓度呈现由井筒中心向深部储层逐渐扩散的趋势，且在同一距离处的质量浓度随注水时间的增加而增加；从图5可知，越远离井筒中心，细菌和营养物质量浓度逐渐降低；距离井筒中心1.1 m处细菌质量浓度随时间的增加幅度最大，由5 d的16.88 g/L增长到20 d的30.97 g/L，超过1.1 m以后增幅逐渐减小。此外可知，营养物扩散程度略高于细菌扩散程度，与营养物是细菌适宜生长前提条件这一自然规律一致。

3.3 注水速率对细菌堵塞储层的影响

保持其他条件恒定，考察不同注水速率下细菌对储层的堵塞，结果如图6所示。保持注水平均速度为0.36 m/d、连续注水10 d，细菌会导致以注水井眼为中心、半径2 m的椭圆形堵塞区域内的堵塞扩散程度高、储层损害严重，损害后平均渗透率仅为原始渗透率的17.8%；若采用1.56 m/d的较大注水速度连续注水10 d后，细菌导致的椭圆形堵塞区域面积变小，但形成椭圆形堵塞区域的长轴更长，2 m损害带半径范围内的平均渗透率为原始渗透率的29.5%，大于注水速度0.36 m/d时的渗透率。由此可见，当注水速度增加时，含细菌、营养物流体会呈现单方向突进现象，而低注水速度会使注水井周围出现较大程度的细菌堵塞，因此在注水过程中适当增加注水速度可防止或减轻细菌堵塞。

图6 不同注水速度下储层损害分布Fig.6 Distribution of reservoir damage under different water injection rates

3.4 温度对细菌堵塞储层的影响

在储层恒温以及因外来水注入储层导致储层温度下降的两种情况下讨论温度对细菌堵塞储层的影响。数值模拟中只考虑均质情况，因此x和y方向的模拟数据对称。

注水速度为0.36 m/d时，温度对细菌损害储层的影响及储层温度分布如图7所示。图7(a)中将储层温度设定为60 ℃，注水进行1 a后井周储层出现堵塞情况，越靠近井筒渗透率越低，且堵塞区域呈现定向扩散的形式；距离井筒2 m之内的蓝色区域储层堵塞最为严重，储层平均渗透率降低到原始渗透率的43%。

由图7(b)、(c)可知，在实际注水过程中，注水储层温度往深部是逐渐增加的。利用前述注水导致储层温度下降而使储层温度呈分布态的细菌堵塞模型，根据模拟结果可知，堵塞最严重的蓝色区域由原来恒温状态的2 m增加到4 m，在损害带半径为4 m的范围内，储层平均渗透率降低到原始渗透率的50%,储层温度为36～54 ℃；同时，损害带半径为1 m的范围内，细菌对储层的损害程度最大，细菌的最大生长速率也最大(图8)，且该空间的储层温度低于47.3 ℃，即低于47.3 ℃最有利于细菌生长，造成严重的细菌堵塞；距离井筒越近、温度越低、损害越严重；距离井筒越远、温度越高、损害越轻微。

图7 温度对细菌损害储层的影响Fig.7 Influence of temperature on bacterial damage reservoir

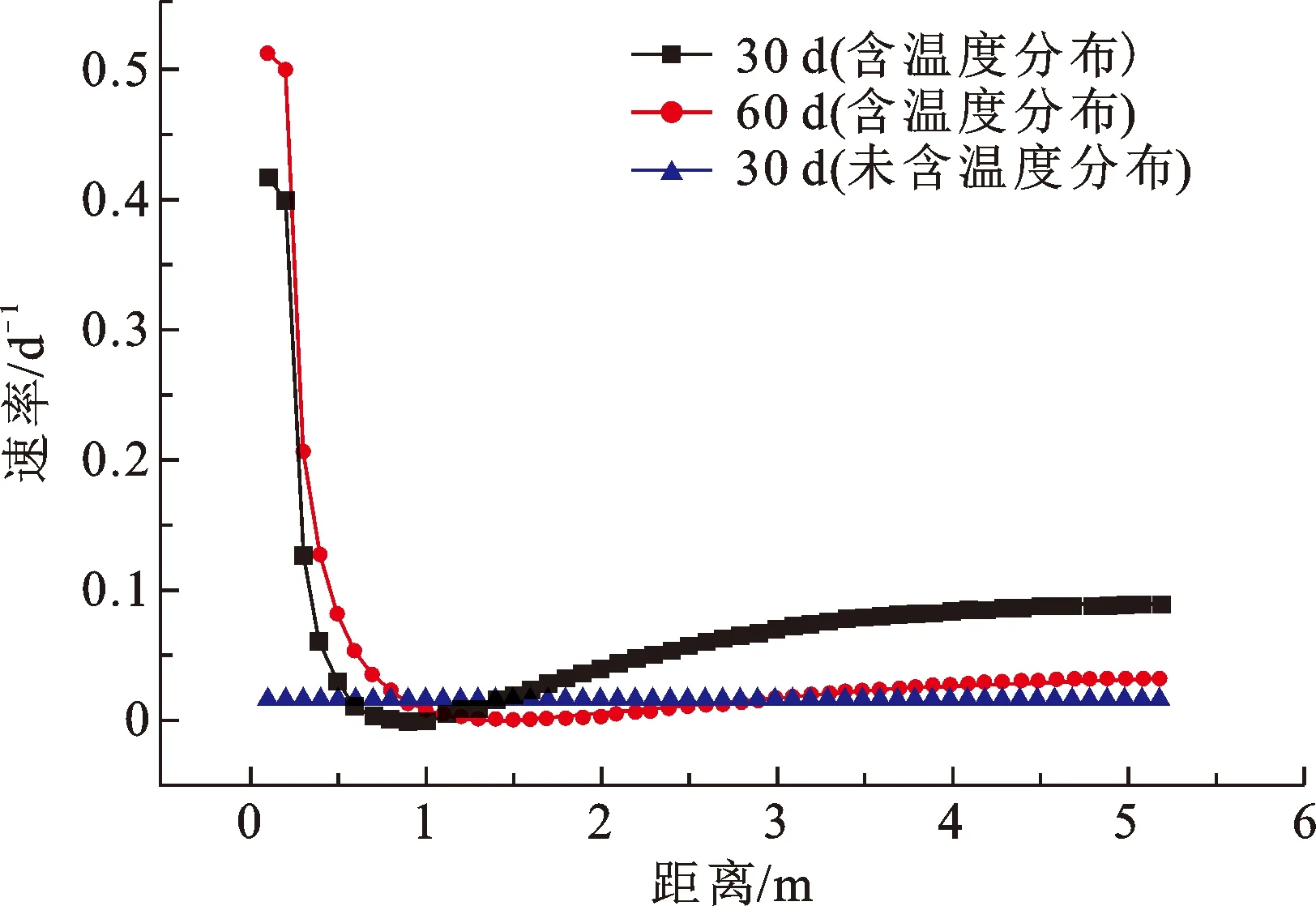
图8 细菌最大生长率分布Fig.8 Distribution of maximum growth rate of bacteria

4 结 论

(1)基于传热传质理论建立矿场尺度下细菌堵塞储层时空演化数值模型，可实现储层损害规律随空间和时间演化的定量模拟，且具有较高的准确性。

(2)注水速率对细菌堵塞影响较大，低速率注水造成井筒周围普遍堵塞,高速率注水会在储层产生单向低渗透率区域，适当增加注水速率有助于防止细菌堵塞。

(3)注水过程中近井壁处形成温度分布带，温度低于47.3 ℃时由于更利于细菌繁殖，而会造成更严重储层伤害。