基于粒子滤波的列车轨道占用判别方法
袁 祎,陈光武,李朋朋 ,刘 洋
(兰州交通大学 a.光电技术与智能控制教育部重点实验室,b.自动化与电气工程学院,c.甘肃省高原交通信息工程及控制重点实验室,兰州 730070)
由我国北斗卫星导航、欧洲ALILEO、美国GPS、俄罗斯GLONASS 组成的全球导航卫星系统(Global Navigation Satellite System,GNSS)已广泛应用至各领域.在铁路领域中,基于GNSS 的列车定位系统减少了传统意义上轨旁设备的铺设、降低了建设和运营成本、同时提高了铁路运输的效率,满足了下一代列控系统要求列车自主获取位置信息的需求,而基于卫星的列车定位方式作为铁路关键安全应用中的一部分,对其可靠性与安全性提出了更高的要求[1-3].在此基础上,准确判别列车所在轨道区段是近年来的研究热点[4],但是GNSS 在线路盲区内,不满足定位精度要求,无法保证其可靠性及安全性要求.因此,基于GNSS/INS 的组合定位系统配合高精度的数字轨道地图弥补了这种不足[5],但对于列车轨道占用的判别,仅仅依靠定位信息的精度无法保证,目前使用GPS 定位的青藏线ITCS 系统,利用联锁信息或应答器信息辅助实现列车的轨道占用判别,但这种方式缺乏判别自主性,还是要很大程度依靠外源信息.
鉴于此,一些文献也提出了各种轨道占用判别方法,如文献[6]将HMM 模型应用至轨道占用识别过程中,对列车运行轨迹进行了有效的识别.文献[7]提出基于道岔曲线的列车定位方法,其通过GPS/IMU 获取列车运行特征,并与线路信息进行匹配,实现轨道占用判别.文献[8-9]利用车载惯性传感器获取列车运动状态,建立列车航向角运动学模型,通过分析模式类型判断轨道占用.文献[10]提出了以多源定位信息融合为前提,基于多位置假设的垂直投影地图匹配方法.文献[11-13]对列车位置假设进行贝叶斯建模,剔除小概率假设所需距离,改进了垂直投影的方法,实现轨道占用判别.文献[14]通过GNSS 双差定姿配合改进粒子滤波提高姿态信息精度,利用分类算法进行轨道占用判别.文献[15]则利用GNSS 数据中的距离与方向信息,建立多条线路的权重函数实现判别.上述研究均取得一定的效果,但是在采样频率低、定位间隔较大的运行情况下,并不能保证判别的实时性,同时也没有结合列车位置决策的预判别,往往会产生一定的距离延迟.
考虑以上方面,本文作者提出一种基于粒子滤波的列车轨道占用判别方法.以PF 原理为基础[16]辅以轨道电子地图,采用粒子跟踪的思想对列车轨道占用判别的过程进行建模,通过可变误差置信区域对与当前定位点相邻的地图数据库中的道岔节点进行检索获取,沿与之拓扑连接的轨道区段初始化随机生成粒子,随列车运动模型实时更新粒子并计算距离及方向综合权重,最后分析计算与道岔节点拓扑邻接各道岔区段中累计的粒子权值,得出占用概率最大的轨道区段,完成轨道占用的正确识别,并设计对比实验验证了算法的可行性.
1 GNSS 列车轨道占用判别问题描述
列车轨道占用判别问题可描述为如图1 所示的过程,当GNSS 接收机所采集到的列车位置信息在处于道岔区段时,由于自身误差影响,实际定位点离道岔区段正向距离L1与侧向距离L2相等,单一采用直接投影判别的方式,无法判断当前列车占用的实际道岔正向区段,从而影响列车实时定位功能的实现,通常主要应用于铁路站场内多平行股道及区间内道岔区段2 种场景,轨道占用判别方法旨在解决当位置传感器无法消除时,如何满足高精度定位的需求,利用算法对列车当前占用轨道进行识别,并确定所在轨道区段的相对位置.
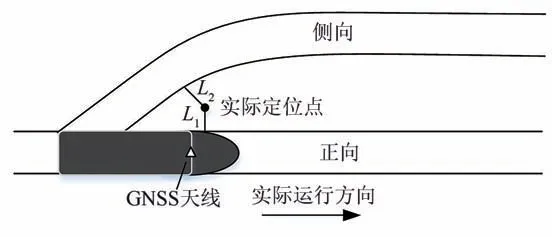
图1 列车轨道占用判别过程Fig.1 Detection process of train track occupancy
2 基于粒子滤波的列车轨道占用判别
2.1 候选轨道线路预识别
根据接收机自身误差设定置信区域,以当前定位点为中心进行线路道岔节点的搜索,当搜索到拓扑节点存在多条候选轨道信息时,进入列车轨道占用判别环节,如图2 所示.

图2 误差置信区域示意图Fig.2 Schematic diagram of error confidence zone
通过设定基于GNSS 定位数据获得置信区域,并分析与候选道岔区段的拓扑关系,完成对候选道岔区段的处理,构建动态调节误差椭圆进行路段的检索,可根据列车实时运行速度调整检索区域,提高道岔节点的搜索效率.设定当前定位点坐标在高斯平面坐标系下为(xi,yi),以原始定位点为误差椭圆中心,其参数可描述为

式中:a、b、φ分别为误差椭圆长、短半径及偏转角;和为(xi,yi)定位点的东向、北向测量误差的方差;σxy为协方差,其值通过GNSS 定位解算的量测方程直接获得;σ0为单位权值的后验方差,需根据不同可信度引起σ0的改变而调整路段检索区域的大小;kv为速度调节因子;v为当前列车运行速度;vmax为最高运行速度.根据而列车实际运行情况,本文取最大值为110 km/h.
则当前定位点(xi,yi)与对应候选道岔区段中点满足
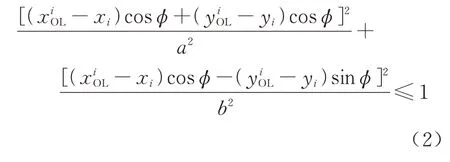
若存在两条及以上线路满足式(2)条件,则进入列车轨道占用判别过程,检索得到当前道岔节点.
2.2 粒子的生成方法
每个道岔节点相邻的候选区段l{l1,l2,…,ln}均 由m个数据 点p{p1,p2,p3,…,pm}构 成,首先以当前定位点(xi,yi)为准,利用误差置信椭圆搜索到与之最接近的道岔节点,将其所邻接的候选轨道区段作为粒子生成区间,如图3 所示,在生成区间内进行初始化产生k个随机粒子o{o1,o2,o3,…,ok},且粒子候选道岔区段的产生概率是随机的,因此通过随机生成索引k∈[1,2,…,T],从候选道岔区段中选取生成区间,再根据随机生成长度比例因子,在此区间内生成粒子.具体步骤如下:

图3 粒子的生成示意图Fig.3 Schematic diagram of particle generation
1) 计算获取候选道岔区段ln各相邻数据点之间的长度

2) 计算候选道岔区段各子弧段累计长度比例

3) 计算初始化生成粒子坐标(r)

2.3 粒子权重的计算
各时刻粒子的权重ω通过建立实时定位点与候选道岔区段生成粒子之间的距离偏差及航向角偏差,进行综合计算,其计算步骤如下:
1) 距离偏差函数的确定.
利用高斯概率密度函数拟合距离偏差,以生成粒子距列车实时定位点的距离,作为函数输入,将距离偏差函数pd设定为

式中:σ为GNSS 误差的标准差;||pi-oi||为当前观测点至生成粒子的距离.
2) 方向偏差函数的确定.
GNSS 的航向角通过当前列车定位点与前一点定位点方向差计算获得αn=θ(on-1,on),参照文献[15],候选道岔区段的方向βn规定为

式中:pni为候选道岔区段;ln为所包含数据点;i为当前候选路段ln包含数据点个数.
实时定位点的速度方向与占用轨道区段的方向应该一致,故其瞬时速度方向与候选路段生成粒子的夹角越小,其权值越大;方向偏差值越大,则权值函数值越小,将方向偏差函数pφ设定为

式中:Δφ为方向偏差,以正北方向为参照基准,列车运行速度与正北方向夹角为αn,而生成粒子与正北方向夹角为βn,则

综合距离因素和方向因素,粒子的权重

2.4 基于粒子滤波的列车轨道占用判别方法
首先以搜索到的道岔节点所邻接的候选轨道作为粒子生成区间,进行初始化,产生随机粒子,建立列车在道岔轨道区段的运动模型,对候选轨道区段的粒子进行实时更新,由于所处道岔区段,列车运行的过程近似为匀速运动,故建立如下列车运动模型更新下一时刻粒子状态.
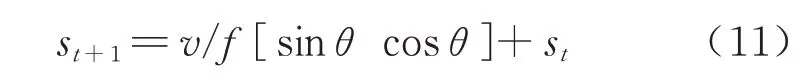
式中:f为采样频率;θ为列车运行方向与正北方向顺时角 度;st为列车t时刻坐 标;st+1为t+1 时刻的列车位置预测.

图4 算法实现流程图Fig.4 Algorithm implementation flowchart
利用PF 原理将轨道占用判别过程建模为列车运行位置与线路地图候选区段的实时匹配过程.其步骤如下.
1)设定可调节误差置信区域,对轨道线路地图中与当前定位点相邻的道岔节点进行搜索,若存在多条轨道线路满足检索关系,则存在道岔节点,进入列车轨道占用判别过程;而后,沿与之拓扑连接的轨道区段初始化随机生成粒子.
2)生成粒子根据式(11)列车运动模型分别沿所在道岔区段移动,进行状态的实时更新.
3)以PF 原理为基础,计算得到各时刻粒子运动状态与列车定位点间的距离误差及航向误差,通过加权函数计算得到粒子权重.
4)计算与道岔节点拓扑邻接各道岔区段中累计的粒子权值,若存在累计粒子权值最大的道岔区段,则将其作为判别结果完成轨道占用的正确识别;若不存在,则归一化粒子权值,并对粒子进行随机重采样,选择权值较大的粒子作为新的生成粒子,返回步骤2),通过构建好的列车运动模型对下一时刻的粒子状态进行实时更新.
随着列车的运行,再通过搜索新的道岔节点进入下一个判别过程,重新生成粒子以进行下一次的列车轨道占用识别.
3 实验结果与分析
3.1 实验描述
采用UB40M 卫星定位板卡进行卫星数据的采集,其输出频率设定为10 Hz,惯性单元采用3DMIMU200A,硬件设备安装见图5,实验路线为北京环形铁路部分线路,采集测试数据长约9 km,Google Earth 中显示的铁路线路及采集到的实测列车轨迹数据见图6,数字轨道地图从Openstreet Map 获取,算法采用Python 语言实现.实验以6 组实测道岔数据为依据,并且实际跑车4 次,以验证本文所提算法的性能.以实验环境中的道岔区段长度平均值为参考,本文算法测试中的高斯概率密度函数标准差σ设为100 m;根据实验环境的路线复杂度,将随机粒子个数o设置为50.

图5 设备安装示意图Fig.5 Schematic diagram of equipment installation

图6 实测列车轨迹示意图Fig.6 Schematic diagram of measured train trajectory
3.2 实验结果及分析
采用基于PF 的轨道占用判别方法,对4 次采集路线中的6 组道岔实测数据进行轨道占用识别结果的统计,如表1 所示,本文所提方法均能得到正确的判别结果.

表1 轨道占用判别方法结果Tab.1 Results of the track occupancy detection method
图7 统计了对采集6 组道岔实验数据分别采用直接投影法、加权识别法及本文提出的基于粒子滤波的判别方法完成轨道占用识别过程4 次的平均距离,可以发现对于实测铁路线路而言,本文所提方法采用粒子跟踪的思想,很好地优化了轨道占用判别的过程,采集到的6 组道岔区段的列车轨道占用判别效果明显优于其他两种对比算法,其平均识别距离比直接投影方式稳定识别占用轨道的距离减少了约6.5 m,比加权识别方法减少了约3.8 m.

图7 完成列车轨道占用判别过程的平均距离Fig.7 Average distance to complete the train track occupancy detection process
列车轨道占用判别算法的性能与列车运行轨迹采样点的密度密切相关,而轨迹采样点受列车运行速度及采集设备的输出频率影响,通常,对于型号特定的道岔,由于其长度固定,则列车运行速度v、定位数据输出频率f及轨迹点个数N满足以下关系

式中:C定义为轨道模板起始点与终止点的距离,通常长度为定值.故在C与f一定的条件下,列车速度v与所能得到的运行轨迹点个数成反比关系.列车运行轨迹点数越少,则列车轨道占用判别算法稳定识别所需距离越长,实时性越差.故列车通过道岔的速度越高,要使列车定位轨迹点足够保证识别算法的有效性,则其输出频率需相应提高,但其成本也会随之增加.
根据通过道岔的列车最大行驶速度,可将实测数据中的6 组道岔场景分为3 组,如表2 统计了输出频率相同情况下,在不同速度条件下采用不同方法完成轨道占用判别的4 次平均距离.以列车实际行 驶速度10 m/s、15 m/s、20 m/s 为3 组场景划分条件,采用直接投影法、加权识别法进行对比.可以看出本文所提方法在行驶速度较高的道岔场景下,均能对列车所占用轨道区段进行准确的识别,相较于其他两种方式,其完成判别过程的平均距离更短,但列车行驶速度越高,在输出频率不变条件下,其获取的轨迹点越少,完成轨道占用判别过程的距离也会相应延长.在20 m/s 的行驶速度下,本文比直接投影方式的判别距离减少8.6 m,比加权识别法的判别距离减少了4.7 m,通过生成粒子跟踪进行匹配得到正确轨道判别结果的方法在定位间隔大、缓和曲线处航向变化不明显的情况下,也能实现轨道的正确判别,与其他方法相比更具实时性.

表2 不同速度下完成列车轨道占用判别过程的平均距离Tab.2 Average distance to complete the train track occupancy detection process under different velocities
4 结论
1)利用PF 原理将轨道占用判别过程建模为列车运行位置与线路地图候选区段的实时匹配过程,在候选道岔区段上随机生成粒子进行列车的实时追踪,提高了轨道占用判别的实时性与准确性.
2)在粒子权值的计算上综合距离及方向因素,可以提高粒子权值计算的准确度,缩短判别过程,避免单一以距离进行权值计算造成判别时效过长的情况.
3)本文提出的方法为列车轨道占用判别提供了新的思路,计算过程具有相对独立性,考虑线路拓扑关系,设置依据车速调节的误差置信区域进行道岔节点的搜索,提前预判是否进入轨道占用判别逻辑,建立列车在道岔区段的匀速运动模型,并使用随机重采样的方式,选择权值较大的粒子进行粒子的更新,对下一道岔节点进行判别时,再重新生成粒子,避免粒子退化现象的产生.实验结果表明,本文能正确识别列车占用道岔区段,并且比直接投影及加权识别方式更具实时性,判别距离更短,具有一定的工程实用价值.
后续将考虑融入多传感器信息,对模型进行优化,从而能够适应复杂运行环境下的列车轨道占用识别过程.

