非屏蔽电缆束的串扰抑制措施研究
崔 勇,谢路雨
(北京交通大学 电子信息工程学院,北京 100044)
电缆在电子产品及电子系统中都扮演着重要的 角色,是用以传输数据、传输电(磁)能、实现电磁能转换和构成自动化控制线路的基础产品,广泛运用于几乎所有的电子电气系统中.
在实际情况下,特别是在航空电子系统和铁路信号传输系统中,由于使用电缆的场合越来越多,对占用空间和敷设场合的要求也越来越高,电缆通常根据其类型和功能打包成一个电缆束,且电子设备的数量大幅度增加,灵敏度不断提高,各种设备连接网络会越来越复杂,信号电缆的电磁干扰与电磁兼容性的问题也日益增多.所以对电缆束的线间串扰问题研究以及提出抗干扰的相关措施是非常紧迫和必要的.
对于电缆束的线间串扰研究通常使用Paul 提出的多导体传输线理论(Multiconductor Transmission Lines,MTL)[1].对于屏蔽电缆的研究,使用转移阻抗把电缆串扰模型分成内回路和外回路分别计算[2-4].早期计算机性能有限,随着电缆数量增多,其串扰计算矩阵增大,Guillaume Andrieu 提出“等效电缆束”方法,说明此方法具有缩短计算时间的优势[5-7],但现今的高智能计算机可以计算大规模矩阵运算,运算时间不再成为难题.对于非屏蔽电缆串扰抑制措施,前人的研究主要集中在干扰线与受扰线之间的距离、线缆的高度、线缆的长度提出相应的线间抗干扰措施[8-9],但这些基于基础理论分析得到的结论在实际中并不实用.而对于屏蔽电缆的串扰抑制措施,重点在研究屏蔽层接地方式对线间串扰的影响[10-11].
基于以上问题,本文作者使用传统的MTL 方法结合模式理论、传输线级联理论建立由链路参数表征的MTL 方程的非屏蔽电缆束数学模型,从电缆束的线缆数量,线缆端接阻抗以及线缆在电缆束中的层位置方面进行研究.由于传统MTL 方程中每根线缆的电压和电流相互影响,致使求解非常困难,通过链路参数方程求解有利于克服此缺点,并且能够直观表达出传输线始端与终端的关系,使用级联的思想也使得计算更精确合理.
1 算法介绍
1.1 多导体传输线理论介绍
假设有已知根长为L的传输线平行分布在地平面上,见图1,每根传输线分别与地构成回路,其中单独的一根传输线作为干扰线,一端接理想电压源Vs并串联电阻ZS1,另外一端有接地负载Zl1,其余线缆布线结构为线束型,均称为受扰线,受扰线近端、远端负载分别为ZSi、Zli.定义近端端口输入电流矩阵为I(0),端口电压矩阵为V(0),远端端口输出电流矩阵为I(L),端口电压矩阵为V(L).

图1 电缆束串扰模型Fig.1 Cable crosstalk model
据图1 列出的MTL 方程为[12]
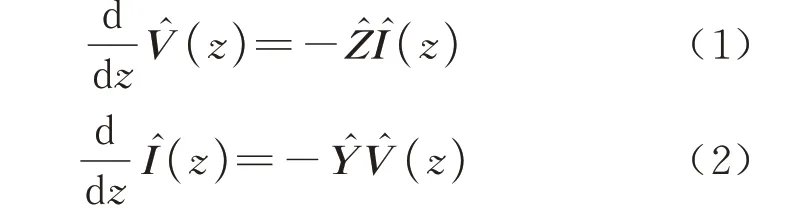
对z进行求导,可得二阶传输线方程

1.2 模量变换介绍
将实际的电压和电流进行如下模量变换

其中

这里就转变成了求解典型矩阵特征值、特征向量的问题.
用乘以式(9)两边,得到

式中:E是单位矩阵是n×1 阶的特征向量,也是需要求解的未知向量.
如果式(13)的系数矩阵的行列式为0,式(13)将有唯一解,即让

从而模电压和模电流的方程式(7)和式(8)可以直接得到它的通解为

通过式(15)和(16)代入式(7)和(8),可以将求得的模电压和模电流变换到传输线上实际的电压和电流,即
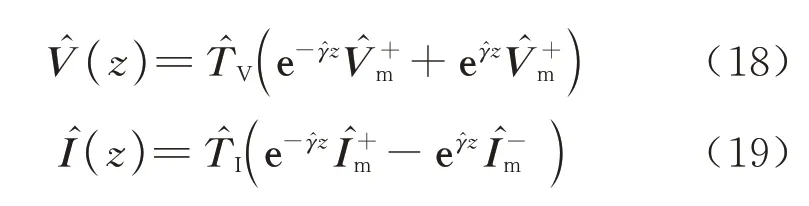
式(18)和式(19)中包含4n个待定系数:4 个n×1 阶的向量可以通过定义特征阻抗矩阵建立它们之间的关系,从而将待定常数的个数降低到2n个.
将式(19)代入式(2),可得

定义特征阻抗矩阵

待定常数的个数降低为2n个.确定了和就可以得到沿传输线任意位置z处的电压和电流值.
利用端口广义戴维南等值方程消去式(22)和式(23)的待定系数和,并得到表征传输线两端相量电压和电流间关系的链路参数矩阵,从而求得传输线始端、终端的电压和电流.
1.3 链路参数矩阵介绍
由式(22)和式(23)给出的MTL 方程的通解中包含了2n个和决定的待定系数,这些待定系数由z=0 和z=L处的终端条件来提供,如图2 所示,最终确定两端的电压和电流.

图2 n+1 导体传输线两端约束网络模型Fig.2 Constrained network model at both ends of an n+1 conductor transmission line
这里端口广义戴维南等值方程为


如图3 所示,传输线两端相量电压和电流间的关系可由链路参数矩阵表征为

图3 由链路参数矩阵构成的2n 端口形式Fig.3 2n-port form consisting of the link parameter matrix

式中:为链路参数矩阵.
计算式(22)和式(23)在z=0 和z=L处的值,并消去,得到

根据式(28)和式(29),可以得到链路参数子阵为

从而可以得到式(27)的链路参数矩阵.
基于级联传输线理论,可以将具有分布参数的多导体传输线划分为多段,每段近似为均匀多导体传输线,它们以串联的方式连接,如图4,这样每一小段的串扰模型就是1.1 节和1.2 节推导的多导体传输线的串扰模型.将传输线的长度划分为n部分,每部分 的链参 数矩阵 分别为,级联传输线总的链路参数矩阵为各段传输线链路参数矩阵的乘积.即

图4 级联传输线模型Fig.4 Cascaded transmission line model

联立链路参数方程和端接方程式(24)和式(25),便可求得近端和远端串扰电流值.

2 验证算法
对8 导体传输线中3 号受扰线进行研究,通过对比本文算法计算值、CST 仿真值、等效后算法计算值、等效后 CST 仿真值,发现等效电缆方法在仿真的较高频范围内误差很大,而本文算法相比于等效电缆方法误差减小,说明本文使用算法对线间串扰的计算是十分有效的,并且等效电缆方法本身就是多次等效的结果,对于电缆束的串扰研究不具有实用性,所以本文的方法具有一定的先进性和合理性.对比结果见图5.

图5 本文算法计算值、CST 仿真值与等效电缆方法对比Fig.5 Comparison of the calculated values for the algorithm,CST simulation values and the equivalent cable method
3 仿真分析
3.1 不同数量的受扰线缆对线间串扰的影响
根据第1 节推导的数学模型,编写计算程序求解受扰电缆束在不同数量下的串扰耦合系数,将求解结果与 CST 软件仿真结果进行对比.本文将对以下3 种电缆模型进行研究,见图6.根据控制变量法,只以电缆的数量为变量,其余的条件不变,设置参数:选取电缆长度为4 m,距地高度10 cm,干扰线与所研究的受扰线相距s=10 cm.选取干扰电缆和受扰线缆均为直径2.2 mm 的普通铜线电缆,干扰线负载与受扰线负载均取50 Ω.仿真频率范围为1 kHz~100 MHz.
1)平行双线传输线中干扰线对受扰线的串扰影响,其中r为导体半径,见图6(a).
2)平行三线传输线中干扰线对2 号受扰线的串扰影响,其中d=1 mm,见图6(b).
3)8 导体传输线中干扰线对2 号受扰线的串扰影响,见图6(c).

图6 传输线横截面设置模型Fig.6 Setup model of transmission line cross section
根据图6 所示的3 种传输线模型,研究不同受扰线数量对线间串扰的影响.
对比结果如图7 所示.可以看出,在100 kHz 以下,模型计算结果与 CST 仿真趋势基本一致,受扰线束中线缆的数量对串扰耦合系数并没有明显影响;在100 kHz 以上,随着受扰线束中线缆数量的增多,干扰线对相同位置的受扰线之间的耦合系数依次减小,即平行双线中的受扰线串扰耦合系数>平行三线中的2 号受扰线串扰耦合系数>8 导体传输线模型中的2 号受扰线串扰耦合系数.因此,对于电缆束的干扰抑制措施,可以提出如下建议:尽量以电缆束的结构传输信号,电缆束中电缆的数量应在条件允许的情况下尽可能多.

图7 三种模型下近端串扰耦合系数比较Fig.7 Comparison of NEXT coupling coefficients under three models
3.2 受扰电缆束不同层电缆产生的线间串扰影响
考虑受扰电缆束中不同层的电缆产生的线间串扰影响,对实际的三层电缆束结构进行研究,根据控制变量法,对19 根电缆束的中心层(红色)、中间层(蓝色)、最外层(绿色)分别选取线缆进行研究,选择1、3、6、11、17 号电缆进行仿真计算.可知受扰线距离干扰线越近其线间串扰越大,为了说明受扰电缆束中不同层的电缆产生的线间串扰影响,选择距离因素最明显的1、2、5、9、15 号电缆进行仿真对比,观察其层数和距离的影响.三层电缆束结构的横截面模型如图8 所示.设置参数如下:选取电缆长度为4 m,距地高度10 cm,s=10 cm,负载阻抗均取50 Ω.仿真频率范围为10 kHz~100 MHz.

图8 受扰电缆束19 线三层结构模型Fig.8 19-wire three-layer structure model of disturbed cables
根据图8 所示的受扰线三层结构模型,研究不同层的电缆产生的线间串扰影响,得到仿真结果如图9 所示.
由图9(a)可以看出,在400 kHz 以下,1、3、6、11、17 号电缆的串扰耦合系数基本一致,不同层的电缆产生的线间串扰并没有明显影响;在400 kHz~2.5 MHz,线间串扰耦合系数大小保持着11 号>3 号>1 号>6 号>17 号,说明此时线间串扰以受扰线和干扰线间的距离为主要影响因素;在2.5 MHz 以后的高频段,不同层的电缆串扰耦合系数开始变化,过渡 到11 号>17 号>3 号>6 号>1 号,即最外 层电缆串扰耦合系数>中间层电缆串扰耦合系数>中心电缆串扰耦合系数,此时表明受扰线和干扰线间的串扰逐渐以电缆的层位置为主要影响因素,这是因为中心电缆被其他电缆包裹可以达到类似电场屏蔽的作用,而11 号>17 号说明层位置相同时,其串扰受干扰线和受扰线间的距离影响.

图9 受扰电缆束中不同层的电缆产生的线间串扰影响Fig.9 Effect of wire-to-wire crosstalk from cables in different layers in a disturbed cable
同样选择距离因素最明显的1、2、5、9、15 号电缆进行仿真对比,结果如图9(b)所示,观察其层数和距离的影响,同上述讨论结果,在仿真范围低频段电缆的串扰耦合系数基本一致,在仿真范围高频段,层位置越向内线间串扰越小.所以,对于电缆束抑制干扰的措施,可以提出如下建议:将重要的信号、易受干扰的信号尽量靠近电缆束的中心位置传输,可以在一定程度上抑制线间串扰.
3.3 受扰电缆束不同端接阻抗对线间串扰的影响
关于受扰电缆束不同端接阻抗对线间串扰的影响,对7 根受扰线组成的电缆束进行研究,见图6(c),选择铁路常用422、485 型号电缆的特性阻抗120 Ω 为本文所研究电缆束端接阻抗,只改变2 号电缆的端接阻抗分别为10、50、100、500 Ω,其余条件不变,用本文方法计算3 号电缆的近端串扰影响,并与CST 仿真结果对比,结果如图10 所示.

图10 改变2 号线端接阻抗,3 号线近端串扰耦合系数变化Fig.10 Change the termination impedance for line 2,and change the coupling coefficient of near-end crosstalk for line 3
由图10 可以看出,本文的方法与 CST 的仿真结果同样能达到非常高的吻合度.在100 kHz 之前的低频段,改变2 号线缆端接阻抗,3 号电缆近端串扰耦合系数没有明显差别,而100 kHz 之后的较高频段,随着2 号线缆端接阻抗减小,3 号电缆近端串扰耦合系数逐渐减小.这是因为电缆束从地平面回流时,若其中1 根连接较小阻抗,那么该回路的阻抗相对最小,起到近似短路作用,而各受扰线回路产生的感应电流均经地平面回流,则总电流经过该阻抗最小回路的回流比例增大,从而其他回路电流有所减小.由此,对于电缆束的串扰抑制措施,本文提出“牺牲电缆”的概念,即可以在电缆束中选取一根电缆作为“牺牲电缆”(如2 号电缆),其端接阻抗非常小的负载,这对于其他线缆(如3 号电缆)线间串扰具有一定的抑制作用,所以应选择其他电缆传输重要信号,“牺牲电缆”不传输有用信号.
4 结论
1)在仿真范围的较高频段,随着受扰线束中线缆数量的增多,干扰线对相同位置的受扰线之间的耦合系数依次减小,所以尽量以电缆束的结构传输信号,并且电缆束中电缆的数量应在条件允许的情况下尽可能多.
2)在仿真范围的较高频段,受扰线和干扰线间的串扰以电缆的层位置为主要影响因素,层位置越向内线间串扰越小,因此对于重要信号、易受干扰的信号尽量放置在靠近中心的位置,这在一定程度上可以抑制线间串扰.
3)在仿真范围的较高频段,随着2 号线缆端接阻抗的减大,3 号电缆近端串扰耦合系数逐渐减大.由此,本文提出“牺牲电缆”的概念,即在电缆束中选取一根电缆作为“牺牲电缆”,其两端连接阻抗非常小的负载,以抑制其他线缆的线间串扰.
由于在实际应用中,受扰线除了是束状的结构,还应具有屏蔽层[15-16],本文的研究重点是电缆束的串扰问题,提出抑制线间抗干扰的具体措施,没有考虑屏蔽层的作用,并且缺乏与现场环境实测值的比较,因此下一步的研究重点将围绕屏蔽电缆的串扰问题并进行现场实测.

