基于深度卷积去噪网络的电能质量扰动识别方法

奚鑫泽，邢超，覃日升，郭成，周鑫

（云南电网有限责任公司电力科学研究院，昆明 650217）

0 引言

随着分布式发电系统以及高速开关设备的大量接入，复合电能质量扰动事件的发生比以往更加频繁，种类更加繁多［1-2］。复合扰动由多种单一扰动按一定规则组合而成，多种单一扰动特征的相互影响给复合扰动分类造成了极大困难［3-4］。传统的扰动特征提取方法包括小波变换［5-6］、S变换［7-8］、集成经验模态分解［9］和变分模态分解［10-11］等，这些方法采用人工方式提取扰动特征，容易造成特征丢失，对复合扰动分类的正确率还有待提高。

近年来，随着智能电网建设的推进，其规划、运行和维护产生的数据量呈指数增长，基于电力大数据的深度学习方法成为研究热点［12-15］。在复合扰动分类领域，也出现了许多先进的研究成果［16-21］。Mohan［17］等人探讨了深度学习算法在复合电能质量扰动识别方面的潜力，对常见的深度网络进行了详细对比分析。文献［18］进一步总结了深度学习算法在复合扰动分类领域应用的一般架构，并提出了网络结构的设计原则和训练策略。这类深度学习方法无需信号处理过程，可以自动提取扰动特征，大大提高了扰动的识别精度。然而，这类深度学习模型强大的拟合能力在面对复杂噪声干扰时容易出现过拟合，抗噪性能不强。因此，有必要开发适用于复杂噪声环境下的电能质量扰动识别新方法。

最近，一种端到端的深度去噪算法——深度残差收缩网络被提出［22］。该方法将软阈值函数与深度学习结构相结合，能够应用于复杂噪声环境下的机械故障诊断任务。本文对深度残差收缩网络进行了改进，并提出了一种适用于高噪声环境下的电能质量扰动识别算法。相比于深度残差收缩网络，本文重新构建了软阈值函数层，并将其作为一个独立去噪模块，插入到卷积层之间，进而增强卷积网络的去噪能力。扰动信号属于一维时间序列，因此本文在一维卷积块的基础上添加软阈值去噪模块，并通过卷积块与软阈值去噪模块的堆叠得到深度卷积去噪网络（deep convolutional denoising network，DCDN）。仿真对比实验结果表明，相比于现有深度学习方法，所提深度去噪网络具有特征提取能力强、抗噪性好等优点，能够有效处理高噪声环境下的复合电能质量扰动识别问题。

1 软阈值去噪网络

基于神经网络构造软阈值函数，并将其插入到深度网络中构成软阈值去噪模块。所构造的软阈值去噪模块对卷积网络输出的特征图进行自适应变换，去除特征图中的噪声及冗余特征。根据对卷积通道的不同处理方式，本文构造了通道共享和通道独立两种软阈值去噪模块。

1.1 软阈值函数

软阈值处理在很多信号去噪方法中经常被用作关键步骤。一般来说，原始信号被转换到一个域，其中接近零的数字是不重要的，因此采用软阈值法将接近零的特征值转换为0，而将其他绝对值较大的特征朝着0的方向进行收缩，它可以通过以下公式来实现。

式中：x和y分别为输入和输出特征；τ为阈值。软阈值函数的导数表达式如下：

上述软阈值函数及其导数的处理过程如图1所示。

图1 软阈值及其导数的处理过程Fig.1 Illustration of (a) soft thresholding and (b) its derivative

从图1（b）可以看到，输出对输入的导数为1或0，这对于深度学习方法在反向传播过程中防止梯度消失和爆炸问题是有效的。因此，采用深度学习网络构造软阈值去噪模块是一种可行方法。相比于软阈值函数，采用深度网络构造的软阈值去噪模块能够针对不同输入特征的含噪情况自适应地计算其阈值，进而有效地减少输入特征中的噪声及冗余特征。

1.2 通道共享软阈值去噪模块

为了能够根据特征样本自身的噪声含量自适应地独立设置阈值，所构建去噪模块中的软阈值应从特征本身变换而来。本文采用一维卷积对扰动信号进行特征提取，因此软阈值去噪模块的输入是卷积网络输出的特征图F，F的尺寸为C×N，其中C为特征图的通道数，N为特征图的序列长度。构造的通道共享（channel shared， CS）软阈值去噪模块如图2所示。

如图2所示，给定输入特征图F，首先取F的绝对值，然后采用全局均值池化（global average pooling， GAP）将二维特征图转化为长度为C的一维向量ff，具体表达式如下。

图2 通道共享软阈值模块Fig.2 Channel shared soft threshold module

式中：fc为一维向量ff的第c个元素；Fc为二维特征图F中通道c的特征向量。然后，采用全连接层对一维向量进行线性变换，得到一个缩放系数α。为了使得缩放系数的数值范围在0到1之间，采用Sigmoid函数作为输出神经元的激活函数。线性变换过程如下。

式中：WC*1为输入维度为C、输出维度为1的线性变换；δ为sigmoid激活函数。接着，将缩放系数与特征图绝对值的平均值相乘得到阈值τ。这样的设计保证了学习得到的软阈值函数的阈值不仅总大于0，且始终小于特征图的最大绝对值，否则，软阈值去噪模块的输出将始终为0。阈值的计算过程如式（6）所示。

式中：i和j分别为特征图通道维度和特征维度的序号。最后，采用式（1）定义的软阈值函数对原始特征图进行软阈值去噪，得到去噪后的特征图F′。

1.3 通道独立软阈值去噪模块

通道共享软阈值去噪模块对整个特征图采用一个统一的阈值进行去噪，具有可学习参数少，结构简单等优点，但考虑到卷积输出的特征图不同通道的特征来源于不同卷积滤波器，具有一定的独立性，使用统一的阈值可能难以适应各个通道的噪声情况。为此，进一步设计通道独立（channel wised，CW）的软阈值模块，其结构如图3所示。

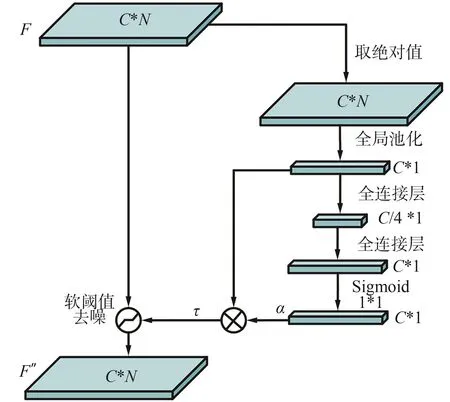
图3 通道独立软阈值模块Fig.3 Channel wised soft threshold module

相比于通道共享软阈值模块，通道独立软阈值模块采用两层全连接神经网络做线性变换，将全局池化后的一维特征向量转化为相同维度的缩放系数向量α，线性变换过程可以表示如式（7）—（8）所示。

式中：W1和W2分别为两层线性变换层，W1输入维度为通道数C，输出维度为C/4，W2的输入输出维度分别为C/4和C；δ为sigmoid激活函数，用于归一化缩放系数；σ为线性修正单元（rectified liner unit，Relu），防止训练过程中的梯度弥散问题。将缩放系数向量α与全局池化后的特征向量相乘得到阈值，其表达式如式（9）所示。

式中i和j分别为特征图通道维度和特征维度的序号。最后，采用式（1）定义的软阈值函数对原始特征图的每个通道分别进行软阈值去噪，得到去噪后的特征图F″。

2 基于深度卷积去噪网络（DCDN）的扰动识别方法

2.1 DCDN网络的整体架构

所提DCDN模型主要包括基于一维卷积的特征提取网络和基于全连接层的扰动分类网络两个部分，其整体架构如图4所示。

图4 DCDN网络的整体架构Fig.4 The framework of DCDN

DCDN网络首先采用特征提取网络对扰动信号进行特征提取。特征提取网络由4组一维卷积块和软阈值去噪模块交替堆叠而成。采用多个全连接层（fully connected layers，FC）构造扰动分类网络，最终输出扰动的类别标签。在特征提取网络与分类网络之间，采用最大值全局池化层进行连接。所提DCDN网络的扰动识别过程可以表示如式（10）所示。

式中：x为扰动信号（一维时间序列）；f1DCNN（·）和fFC（·）分别为特征提取网络和扰动分类网络；y为扰动的类别标签。

2.2 一维卷积块

所提DCDN模型的特征提取网络采用一维卷积神经网络（one-dimensional convolutional neural network，1DCNN）进行构建。一维卷积只对输入数据的一个维度进行卷积运算，运算过程在数据的空间维度上滑动进行，适用于提取一维序列数据（如扰动信号）的特征，其映射过程如式（11）所示。

式中：m为卷积核的大小；kj为卷积核第j个权重系数；b为卷积的偏置；fi为卷积的第i个输出值；对应于输入序列的第i个值xi；δ（·）为卷积输出的非线性激活函数。

特征提取网络的每个卷积块由2个一维卷积层和1个最大值池化层构成。输入的序列采用两个卷积核较小的卷积层进行连续卷积，以增加卷积层的感受野。最大值池化层能够对卷积输出的特征图进行降维，具有特征筛选的作用，进一步减少了参数量。构建的一维卷积块的参数设置如表1所示。

表1 一维卷积块参数设置Tab.1 The parameters setting of 1DCNN

2.3 扰动分类网络

采用两层全连接层搭建扰动分类网络，2个全连接层之间添加Dropout层，每次训练随机丢弃部分权重连接，提高网络的泛化性能，防止模型过拟合。网络的输出层采用softmax函数作为激活函数，其数学表达式如下。

式中：xi为输出层第i个神经元的输出；pi为第i个标签输出值，表示样本属于第i类扰动的概率值；n为扰动的总类别数。扰动分类网络的详细参数设置如表2所示。

表2 分类网络参数设置Tab.2 The parameters setting of classifier network

2.4 DCDN网络的训练

DCDN网络通过反向传播算法来训练，采用Adam优化算法更新完了权重，可以有效缓解梯度稀疏问题，具有计算高效、所需内存少等优势。为了进一步加速算法的执行速度，采用Mini-batch 方法，即每次迭代输入多个样本。

电能质量扰动识别本质上是一个多分类任务，为了便于网络的训练，采用one-hot向量来表示扰动的类别，如果样本信号中包含第i种扰动类别，则其样本标签向量的对应第i个元素为1，其他原元素为0。one-hot标签结合网络末端的softmax分类器是进行多分类任务的有效组合，通常采用多分类交叉熵计算分类损失，其表达式如式（13）所示。

式中：c为类别总数；pi和yi分别为第i个扰动类别的预测值和真实值。

3 仿真实验验证

3.1 扰动信号仿真数据集

为了验证所提DCDN方法的有效性，采用MATLAB 2019a软件根据扰动的数学模型进行仿真，得到训练和测试样本。根据电能质量的IEEE Std.1159标准，建立暂升、暂降、中断、谐波、闪变、振荡暂态和脉冲暂态7种典型的单一扰动信号的数学模型，电能质量扰动信号的基波频率为50 Hz，采样频率设为3.2 kHz。每个PQD信号样本采样10个周期，共包含640个采样点。单一扰动的仿真波形如图5所示。

图5 单一电能质量扰动的仿真波形Fig.5 Simulated waveforms of single PQD

将以上7种单一扰动进行复合，得到10种复合扰动共计17个类别，具体类别与编号列于表3。

表3 电能质量扰动类别及其标签Tab.3 The types and labels of PQD

采用MATLAB软件制作扰动数据集，每个扰动类别生成1 000个样本，其中600个作为训练集，200个作为验证集，200个作为测试集。最终，得到样本数分别为10 800、3 600和3 600的训练集、验证集和测试集。考虑实际环境中的噪声问题，在上述扰动数据集上添加高斯白噪声，信噪比为20～50 dB之间的随机值。此外，为了充分评估模型的抗噪性能，额外生成信噪比分别为20、30、40、50 dB以及不含噪声的测试集。

3.2 模型的实现与训练

根据本文所提软阈值去噪模块的两种架构：通道共享（CS）和通道独立（CW）设计两个DCDN网络，分别为DCDN-CS和DCDN-CW。采用Tensorflow深度学习框架实现所提两种深度学习网络，训练的迭代次数设为100次，样本的批尺寸大小为128，训练过程损失变化如图6所示。

图6 DCDN-CS和DCDN-CW的训练过程Fig.6 The training histories of DCDN-CS and DCDN-CW

图6（a）和（b）分别为DCDN-CS和DCDN-CW网络的训练过程。可以看到，两个模型都在迭代60次后基本收敛。不同的是，相比于DCDN-CS模型，DCDN-CW模型的训练过程更加平稳，这是因为通道独立的软阈值去噪模块针对不同卷积通道采用不同阈值，使得网络更易于训练。

3.3 仿真结果对比分析

为了验证所提模型的性能，设计并实现以下4种现有的深度学习模型进行对比。

1） CNN：在所提DRSN模型的基础上，去掉网络的软阈值模块，仅保留经典的卷积分类网络的结构。在多层卷积之后，直接添加全连接层和softmax分类器进行分类；

2） Resnet：在上述CNN网络基础上，在每个卷积块的输入输出端添加快捷连接构成残差网络。快捷连接采用卷积核大小为1的卷积层实现。

3） SE-net：在上述CNN网络基础上，在每个卷积块的后面加上Squeeze-and-Excitation注意力模块，构成SE-net。

4） CBAM-net：在上述CNN网络基础上，在每个卷积块的后面加上Convolutional Block Attention Module模块，构成CBAM-net。

对比模型的训练参数与损失函数与本文模型保持一致。采用信噪比分别为20、30、40、50 dB以及不含噪声的5种测试集分别对本文所提DCDN模型和上述4种对比模型进行对比，测试的结果如图7所示（ideal表示不含噪声的理想信号）。

图7 不同噪声条件下各深度模型的分类结果Fig.7 Classification results of different DL models under different noises

从图7可以看到，整体上所提DCDN模型表现最好，CNN和Resnet表现最差。在不同噪声条件下，所提模型的正确率波动最小，其他对比模型在极端噪声环境下（信噪比为20 dB）模型的正确率衰减较大，其中CNN和Resnet模型甚至下降了约10%。这表明相比于4种常见的深度学习模型，本文所提DCDN模型在抗噪性能方面有明显优势。

为了进一步分析不同深度模型之间的表现，模型在5种噪声环境下的平均正确率列于表4。此外，为体现本文所提算法的先进性，分别验证不同深度学习模型的复杂度与实时性，将各个模型的参数量、测试所用时间列于表5。

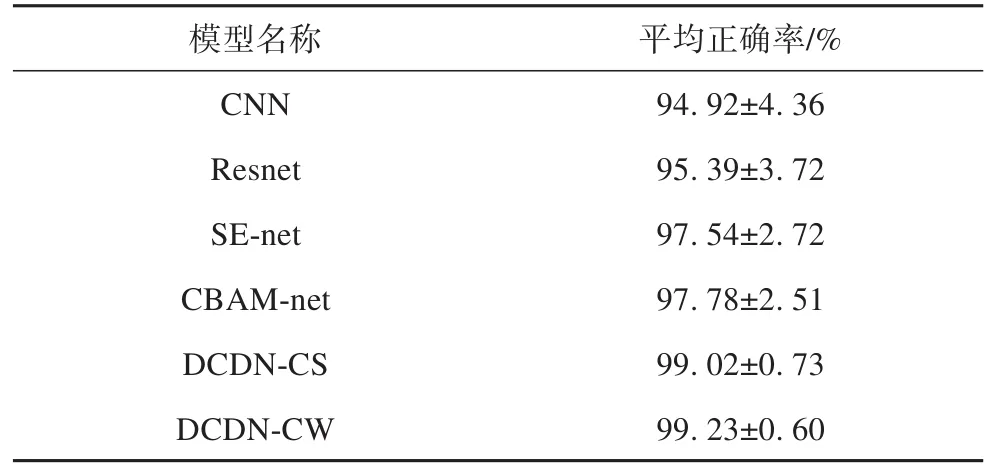
表4 不同模型的平均正确率Tab.4 Average accuracy of different models

表5 不同模型的复杂度Tab.5 Complexity of different models

表4采用均值和标准误统计了各深度模型在不同噪声条件下的平均正确率。可以看到，本文所提深度去噪网络平均正确率均高于99%，且标准误差均小于1%，这意味着所提DCDN网络对扰动信号所含有的噪声具有较强的适应性。相比于经典的CNN网络，正确率提高了约5%。此外，添加了注意力机制的网络SE-net和CBAM-net相比于CNN也有不同程度的提升，这主要是因为引入的注意力机制能够通过分配不同的注意力系数使得模型在训练过程中自动关注有用特征，这与本文所提软阈值去噪网络通过软阈值去除噪声保留有效特征类似。相比于通道共享的DCDN-CS模型，对每个卷积通道独立生成阈值的DCDN-CW模型总体表现也有所提升。

如表5所示，从模型复杂度上来看，相比于经典CNN模型，所添加的软阈值去噪模块并未显著增加模型复杂度，各个模型的参数量基本处于同一水平。总体上，相比于通道共享的DCDN-CS模型，通道独立的DCDN-CW模型参数量更多，模型复杂度也相对更高。

3.4 与现有方法对比分析

将本文所提DCDN方法与现有的电能质量扰动识别算法进行对比，进一步验证所提方法的有效性。分别选择3种传统方法和2种深度学习方法进行对比，3种传统方法包括采用离散小波变换和概率神经网络的方法（DWT+PNN）［5］、采用变分模态分解和决策树的方法（VMD+DT）［11］以及采用可调品质因子小波变换和随机森林的方法（TQWT+RF）［23］，深度学习方法包括采用相空间重构和卷积神经网络相结合的方法（PSR+CNN）［24］和稀疏自编码器方法（SSAE）［25］。与现有扰动识别方法的对比结果如表6所示。

表6 与现有方法的对比结果Tab.6 Comparison results between DCDN and the existing methods

如表6所示，除了SSAE模型以外，本文所提的两个DCDN模型在各种噪声条件下均取得了最高的正确率。相比于SSAE方法，本文方法能够识别18种单一和复合扰动，但识别精度略低，总体上与SSAE的差距小于0.5%。相比于DWT+PNN、VMD+DT以及TQWT+RF等机器学习方法，本文所提方法无需人工提取扰动特征量，简化了扰动识别模型的构建过程，是一种端到端的扰动识别算法。从对复杂噪声的处理情况来看，本文方法在不同噪声水平下的识别正确率波动更小，体现了DCDN方法强大的抗噪声能力。

4 结论

提高电能质量扰动识别算法在复杂噪声条件下的识别精度是进行电能质量扰动识别研究的重要课题。本文基于软阈值去噪的原理设计了两种深度卷积去噪模型：DCDN-CS和DCDN-CW。该方法将软阈值函数作为非线性层插入到深度网络中，使得网络在训练过程中自动去除掉特征图中的噪声或其他冗余特征，提高了深度网络的特征提取能力和对噪声的鲁棒性。仿真实验表明，相比于DCDN-CS模型，DCDN-CW模型对特征图的不同通道设置独立的阈值，具有更高的特征学习能力和扰动识别性能。在各种噪声条件下，所提出的两种DCDN模型不仅优于经典的CNN和Resnet模型，而且优于其他常见的新型深度学习算法，如SE-net和CBAM-net，为复杂噪声环境下的电能质量扰动识别提供了一种有效的解决方案。