基于CFD和时间序列的计量活门阀芯压力预测模型

钟强，何勇，姚凯学，张庆铭，胡加德

(1.贵州大学计算机科学与技术学院，贵州贵阳 550025;2.贵州民族大学数据科学与信息工程学院，贵州贵阳550025；3.贵州科海新技术发展有限公司，贵州贵阳550000)

0 前言

对阀门的建模往往是建立在阀芯受力分析的基础上，由于大部分的阀门都采用液压传动技术，而活门建模中对压力的处理是至关重要的。以往的研究中，主要采用流量连续性定理分析压力[1-6]，将阀口的压力近似为阀芯处所受的压力[4]或者根据泵的工作状态将压力近似为某一函数[5]，亦或是将它作为未知参数，设计控制策略以对它进行调节[6]。某型航空发动机燃油计量系统的模型中存在多个未知参数，这些参数的调节过程复杂，并且系统中的流场是湍流场，系统内的压力变化基本没有规律，因此将阀口或泵的压力近似为阀芯处的压力存在偏差。在实际中，为获得阀芯处的具体数据，通常非常困难而且花费巨大。近年来随着计算机技术和CFD(Computational Fluid Dynamics)计算方法的迅速发展，CFD技术取得了很大的成就，这使得流场数值模拟变得高效且可靠[7]。众多学者已经使用CFD技术对多种工艺的各种特性进行了研究[8-11]，并将计算值与实验所得的结果进行比较，验证了CFD技术的可靠性。对于具有随机性的时间序列数据，可以采用时间序列分析方法进行分析。时间序列数据本质上反映的是某个或者某些随机变量随时间不断变化的趋势，而时间序列预测问题的核心就是从数据中挖掘出这种规律，并利用这些规律作出估计[12]。近些年来,时间序列分析已广泛应用于心理学、地球科学、数据挖掘、数字化误差等各方面，多位学者已经对该方法的有效性进行了验证[13]。因此，本文作者采用CFD方法对活门的流场进行数值模拟，得到其阀芯处的压力数据，结合时间序列分析方法对该数据进行分析，最终建立计量活门阀芯的压力时间序列预测模型。

1 系统工作原理与CFD数学模型

1.1 系统工作原理

燃油计量系统是发动机的“心脏”，燃油计量系统的使命是通过控制燃油来控制发动机。某型燃油计量系统的工作原理如图1所示，电子控制器接收位移传感器反馈信号，并与输入信号作对比，经控制器PI调节后输出计量活门控制腔压力，调节电液伺服阀的流量，进而改变计量活门控制腔压力，使计量活门移动，最终改变计量活门的过流面积，实现燃油计量。电液伺服阀的流量同时也进入了指令活门控制腔，可通过改变指令活门的过流面积实现指令油的释放[14]。

图1 燃油计量系统工作原理

1.2 基本控制方程

某型航空发动机燃油计量系统的流场是一个复杂的黏性不可压缩湍流流场，在定常条件下，可以得到流场的连续性方程：

(1)

1.3 湍流模型

该燃油计量系统的内部存在分离流现象，为更加精确地描述流场，本文作者使用大涡模拟模型进行瞬态模拟计算。大涡模拟模型对流场的初值要求较高，因此先采用κ-ε模型对流场进行稳态模拟计算，再将得到的结果作为初值进行瞬态模拟计算[15]。大涡模拟的思路可以简述为：对大尺度紊流运动直接求解N-S方程；利用次网格尺度模型模拟小尺度紊流运动对大尺度紊流运动的影响。

对于黏性流体，在直角坐标系下时，其运动规律受N-S方程控制，简化不可压缩流体的N-S方程可以得到式(2):

(2)

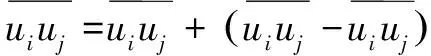
从而得到：

(3)

式中：ui、uj分别为i、j方向的速度分量；p为流体压力；xi、xj分别为i、j方向的位移；t为时间。

2 流场数值模拟计算

2.1 网格划分及边界条件设置

由于燃油计量系统结构较为复杂，选择在AutoCAD软件中进行系统三维建模，随后将该三维模型导入CFD软件中进行网格划分。图2所示为燃油计量系统的三维模型。

图2 燃油计量系统的三维模型 图3 系统网格划分结果

煤油从进油口进入系统，然后通过内部进油口进入计量活门控制腔,作用到计量活门阀芯和指令活门阀芯上，通过出油口流出。因为该系统结构复杂，所以采用非结构网格进行划分，共生成约156万个网格。划分好的网格模型如图3所示。

网格划分完毕后，需进行边界条件设置。该研究中的流体介质为煤油，为不可压缩流体，密度为780 kg/m3、动力黏度为2.4×10-3Pa·s；进口为压力进口，进口压力恒为7 MPa，进口处的流速为10 m/s；出口为压力出口，出口压力恒为6 MPa；壁面均为无滑动壁面。

2.2 仿真结果

将划分好的网格模型导入Fluent软件，设置好边界条件，对流场进行稳态模拟计算。选用κ-ε湍流模型求出流场的初值，在该初值的基础上选用LES湍流模型进行瞬态求解，并在计量活门的阀芯处设置监测器，每一个time step便计算一次阀芯处的压力，共得到4 600个数据。最终得到的系统流场压力分布云图和计量活门阀芯表面压力分布云图分别如图4(a)(b)所示。

图4 仿真结果

从图4(b)可知：在计量活门阀芯表面存在明显的漩涡，并且监测器得到的数据表明阀芯处的压力在(6.7±0.2)MPa范围内随机变动。

3 时间序列原理与压力模型的建立

3.1 时间序列建模原理

设{xt,t∈T}是一个时间序列，称满足如式(4)所示的结构模型为自回归移动平均模型，简记为ARMA(p,q)，

(4)

式中:εt为均值为零的白噪声序列；φ0为常数；p、q为ARMA模型的阶数；φi为待估计的自回归参数；θj为待估计的滑动平均参数。

自回归滑动平均(Autoregressive Moving Average，ARMA)模型是研究时间序列的主要方法，由自回归(Autoregressive，AR)模型和滑动平均(Moving Average，MA)模型混合而成。对于具有时间趋势和周期特征的数据可以进行差分，使它转化为平稳序列。

在自回归移动平均模型中，假设残差序列是满足方差齐性条件的，即残差的方差始终为一个常数。若某一模型的残差服从均值为零，方差是一个随时间变化的量且这个随时间变化的方差是该时间点过去有限噪声值平方的线性组合的正态分布时，该模型称为自回归条件异方差模型(ARCH)。ARCH(q)模型的结构如下：

(5)

式中:系数β0>0,βk≥0,k=1,2,…,q;Xt为前定解释变量，包括被解释变量的滞后项;η为回归参数;εt为独立同分布，εt～N(0,1)；ut为残差项。可见条件方差ht随{ut}过去值的变化而变化。

3.2 时间序列建模步骤

对时间序列建模一般遵循4个步骤：模型识别、模型估计、模型检验和模型应用。

(1)模型识别。根据数据的特征，判断所研究的时间序列属于哪一类，主要检验模型的平稳性，只有当序列通过平稳性检验时才能使用时间序列分析模型。检验的方法主要有DF检验、ADF检验、PP检验、协整检验等[17]。

(2)模型估计。依照样本信息进行模型识别后，得到所分析的时间序列大概的模型类型和模型结构，模型的最终形式还需要估计模型的参数后才能确定。常用的参数估计方法：矩估计、极大似然估计和最小二乘估计等[18]方法。

(3)模型检验。在模型识别时，为简化问题提出了一些假设，因此必须对模型进行检验。时间序列模型的检验有两类：一类是模型的显著性检验；另一类是模型参数的显著性检验，这两类检验统称为模型的诊断性检验。此外，对某些序列，还需要进行ARCH效应检验。

(4)模型应用。时间序列模型的应用主要包括变量动态结构分析、预测和控制。其中预测是时间序列建模的最主要目的，是用已经估计出参数的模型预报变量未来的变化。

3.3 压力时间序列模型的建立

通过流场仿真得到了计量活门阀芯的压力数据共4 600个，该数据是在相同时间间隔内经软件计算得到的具有随机性的一组数据，满足时间序列的特征，可以用时间序列分析方法对该数据进行分析，取前4 500个数据进行时间序列的建模，剩下的部分数据用于模型的预测对比。本文作者使用R软件进行时间序列的建模。

(1)对原始数据进行平稳性检验，常用的方法为ADF(Augmented Dickey-Fuller)检验。ADF检验可以用于3种自回归模型的单位根检验，即不含漂移项和时间趋势项的自回归模型、只含漂移项的自回归模型以及两者都含的自回归模型。表达式分别为

xt=φ1xt-1+…+φpxt-p+εt

(6)

xt=μ+φ1xt-1+…+φpxt-p+εt

(7)

xt=μ+βt+φ1xt-1+…+φpxt-p+εt

(8)

以式(6)为例，将式(6)变形为

xt-xt-1=φ1xt-1+…+φpxt-p-xt-1+εt=

(φ2+…+φp)xt-1+φ1xt-1-xt-1-(φ2+…+φp)xt-1+

φ2xt-2+(φ3+…+φp)xt-2-(φ3+…+φp)xt-2+

φ3xt-3+(φ4+…+φp)xt-3+…-φpxt-p+1+φpxt-p+εt整理得：

(9)

其中：ρ=φ1+φ2+…+φp-1，βj=-φj+1-φj+2-…-φp,j=1,2,…,p-1。

相似地，也可以得到式(7)(8)的单位根检验式为

(10)

(11)

单位根检验的假设条件:

原假设H0：ρ=0(序列非平稳)↔H1:ρ<0(序列平稳)

由此可以构造ADF统计量：

通过蒙特卡洛方法，可以得到τ检验统计量，并进行检验。共有3个ADF检验式，但是针对实际应用中应采用哪一个检验式，DOLADO等建议从式(11)开始检验，若得出的结论为接受单位根假设时，还需谨慎考虑所用检验式是否包含多余的时间趋势项，即也应对φ3统计量进行检验[19]。若φ3统计量的检验结果为接受原假设，则认为用式(11)进行单位根检验不合适，改用式(10)重新进行单位根检验。同理，若式(10)检验结果接受原假设，仍需对φ1进行检验，根据所得结果进一步考虑是否使用式(9)重新进行单位根检验。当序列通过平稳性检验后，便可对该序列进行定阶，以求得其自相关系数图(ACF)和偏自相关系数图(PACF)进而推断模型的阶数，还可以借助AIC准则和BIC准则来进行定阶。用含漂移项和时间趋势项的检验式(11)对数据进行ADF单位根检验，检验结果如表1所示。

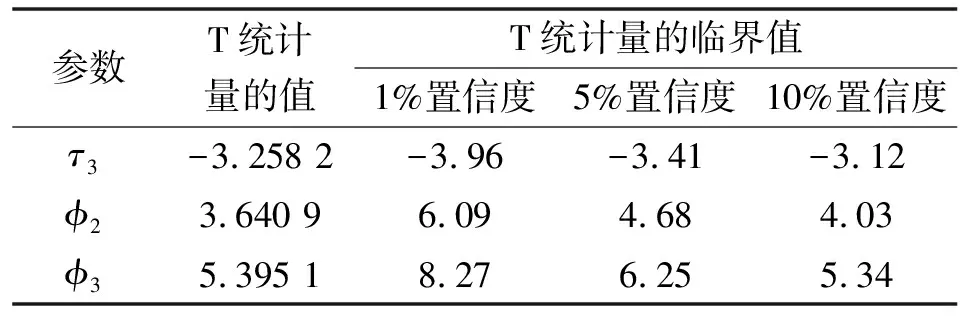
表1 用式(11)对数据进行ADF单位根检验的结果

从表1可以看出:φ3的检验值只比显著性水平为10%的临界值略高一点，这表明用含漂移项和时间趋势项的检验式(11)对数据进行ADF单位根检验是不合适的。因此，进一步选择只含漂移项的检验式(10)对数据进行ADF单位根检验，检验结果如表2所示。

表2 用式(10)对数据进行ADF单位根检验的结果

从表2中可以看出:φ1的检验值比显著性水平为1%的临界值低，这表明用含漂移项的检验式(10)对数据进行ADF单位根检验是不合适的。因此，进一步选择不含漂移项和趋势项的式(9)对数据进行ADF单位根检验，检验结果如表3所示。

表3 用式(9)对数据进行ADF单位根检验的结果

从表3可以看出:τ1的检验值远高于显著性水平为1%的临界值，则接受原假设，即认为该序列是非平稳序列。

此外，本文作者还对原始数据的纯随机性进行了检验，结果表明数据并非白噪声序列，即原始序列具有密切的相关关系，需要对它进一步分析。

(2)由于原始序列非平稳，对序列进行一阶差分，对差分后的序列再进行单位根检验，检验结果表明该序列为平稳序列。求出该平稳序列的自相关系数(ACF)和偏自相关系数(PACF)分别如图5、图6所示。

图5 一阶差分后序列的自相关系数(ACF) 图6 一阶差分后序列的偏自相关系数(PACF)

从图5可以看出:序列的自相关系数在3阶截尾。

从图6可以看出:序列的偏自相关系数在2阶截尾。因此，拟合的ARMA(p,q)模型中,参数p=2、q=3。使用极大似然估计方法对参数进行估计，所得的自回归移动平均模型为

xt=0.109 4xt-1+0.732 3xt-2+ut-0.560 4ut-1-

0.817ut-2+0.525 1ut-3

(12)

式中：ut为残差序列。

(3)对该模型的残差进行白噪声检验，结果表明该序列是白噪声序列。对该序列进行ARCH效应检验，常用的ARCH效应检验方法是LM检验和Portmanteau Q检验。Portmanteau Q检验的思想：如果残差序列方差非齐且具有群集效应，那么残差平方序列通常具有自相关性，故可将方差非齐次的检验转化为残差平方序列的自相关检验。该检验的假设条件[20]为

H0:ρ1=ρ2=…=ρq=0↔H1:ρ1,ρ2,…,ρq不全为0。

其中：ρk表示残差平方延迟k阶的自相关系数。

Portmanteau Q检验统计量的构造为

其中：n为序列长度;ρi为残差序列延迟i阶的自相关系数，表达式为

其中：

若原假设成立，则统计量近似服从χ2分布，其自由度为q-1。因此，当检验统计量Q(q)的P值小于显著性水平时，拒绝原假设，残差平方序列具有自相关关系。使用Portmanteau Q方法对该序列进行ARCH效应检验，检验结果如表4所示。

表4 ARMA(2，3)残差平方的Q检验结果

从表4可知:ARMA(2,3)的Q检验P值均远小于显著性水平0.05，因此拒绝原假设，残差平方序列具有自相关关系，序列的ARCH效应显著。对差分后的平稳序列拟合ARMA(2,3)-ARCH(1)模型，最终模型的各参数如表5所示。

由表5可知:所有参数的P值都小于0.05，即ARMA-ARCH模型的参数拟合是显著的。综上，得到完整的拟合模型为

表5 ARMA-ARCH模型参数估计及其检验结果

(13)

式中:ut为序列的残差项;εt为独立同分布，且εt～N(0,1);ht为残差的条件方差。

(4)使用ARMA(2，3)-ARCH(1)对序列进行预测，并将原序列画出来作为对比，结果如图7所示，其中误差如表6所示。

表6 ARMA-ARCH模型的预测误差

图7 ARMA-ARCH模型的预测结果

从图6可以看出：该模型拟合较好，而且预测到数据在短期内呈上升趋势。

从表6中可以看出:模型的均方根误差小于1，模型拟合较好。

4 结论

(1)在Fluent软件中使用大涡模拟湍流模型对燃油计量系统进行了流场数值模拟计算，并通过在计量活门阀芯处设置monitor的方法获得了计量活门阀芯处的压力时间序列。

(2)使用时间序列分析方法对该序列进行分析，建立了该序列的自回归移动平均模型；对该自回归移动平均模型残差的平方进行了异方差检验(ARCH效应检验)，建立了该模型残差的异方差模型。结合该序列的自回归模型和异方差模型，建立了原始序列的ARMA(2,3)-ARCH(1)模型，使用该模型预测了5个值并与原数据进行比较，结果表明预测效果较好。

(3)研究结果为相关研究中对压力变量的处理提供了参考。