树状微通道散热器强化换热的数值模拟
陈明健,张莹
(南昌大学先进制造学院,江西 南昌 330031)
随着电子设备向小型化、高集成度方向发展,面临着热流密度高、温度分布不均匀的缺点,从而降低了电子设备的寿命和可靠性;因此,如何有效地消除电子设备高集成度所产生的巨大热量引起了众多研究者的关注。树状仿生结构是自然进化演变出消耗能量较小的结构,具有较高传热传质能力。Bejan等[1-3]提出仿生分形微通道,将构造论和熵产生原理相结合,描述了仿生分形微通道的巨大潜力。Chen等[4]通过实验发现在相同的加热功率、温差和入口速度下,树状微通道散热器(tree-like microchannel heat sink,TMCHS)的换热效率比传统的平行微通道散热器要高。Xu等[5]设计了4种不同结构的微通道散热器,发现TMCHS在相同的进口流量下可以带走最多的热量。Xia等[6]基于分形理论,设计了一种适用于主轴冷却的TMCHS,结果表明TMCHS具有更低的压降、更均匀的温度场分布和更大的性能系数。Zhang等[7]通过实验研究了平行、自相似、树状仿生微通道的散热器,结果表明TMCHS的整体换热性能最好。
为了提高TMCHS的换热性能,很多学者做出了努力。Peng等[8-9]通过实验发现TMCHS的换热性能不受形状的限制,既可以做成圆形,也可以做成矩形。微通道的分形角是影响散热器性能的一个非常重要的因素,当分形角度在40°~50°之间时,散热器的热阻较小、散热性能最好。Chai等[10-11]、Xia等[12]研究发现,微通道散热器中的变截面结构可以强化换热能力。Huang等[13]考虑到仿生分形与变截面的耦合效应,设计一种变截面的树状微通道散热器,同样发现变截面结构可进一步提高TMCHS的换热性能。Peng等[14]为了设计出具有良好传热性能和工质流动性能的理想树状分支网络,对树形分支网络的导热系数和渗透率进行了计算,结果表明尺寸、分形角度、分形次数对树状分形微通道有重要影响。Yan等[15]设计了树状结构的个数分别为8,18,20的散热器,结果表明树状结构个数为18的流动换热性能最佳。Xu等[16]研究了凹陷微通道内的流动和换热特性,凹陷表面降低了微通道散热器的局部流动阻力,也改善了微通道散热器的换热性能。Pan等[17-18]通过数值模拟和实验,分析和比较了在侧壁加入不同空腔的微通道散热器的流动和换热特性,相比普通的微通道散热器具有更好的传热性能和更小的压降。Xia等[19]研究了在侧壁加入三角形空腔的微通道,结果表明加入三角形空腔有利于增强换热。基于以上研究可知,加入空腔有利于增强微通道换热能力。
综上所述,本文设计了一种分形次数N=3、分形角度为45°、树状结构个数为18的变截面微通道散热器。采用有限体积法对微通道内的流动和传热进行数值模拟。通过改变微通道的结构以及引入流动干扰技术,在侧壁加入半圆和三角形的空腔来达到强化换热的目的。再通过分析流动特性和传热特性得出了最好的选择。本文的工作为树状微通道散热器的强化换热研究提供了良好的参考。
1 三维树状仿生分形微通道传热模型
1.1 物理模型
如图1所示,本文的物理模型由树状微通道和固体硅基2个部分组成。为了加速收敛速度并提高计算效率,取TMCHS的1/18用于数值模拟。

图1 计算域示意图Fig.1 Schematic diagram of the computational domain
如图2(a)所示,TMCHS的结构参数主要包括:半径R、入口半径Rin、出口半径Rout、分形角θ、分支数n、微通道的宽W、长L、高H、微通道底部和顶部固体高度He。为了研究不同空腔对TMCHS换热性能的影响,建立了图2(b)所示的半圆空腔的树状微通道散热器(tree-like microchannel heat sink-circle,TMCHS-C)和图2(c)所示的三角形空腔的树状微通道散热器(tree-like microchannel heat sink-triangle,TMCHS-T)所示的物理模型。每条流道有10个空腔,空腔的尺寸按式(2)递减。半圆空腔的半径Rc、三角形空腔的高Ht、三角形空腔的底边Lt、空腔之间的距离Ld、空腔与通道入口的距离L0,具体尺寸见表1。分支数n=2,分形角θ=45°。基于分形结构的自相似性,微通道的长度、宽度[14]计算如下:
(1)
(2)
分支级数i,n=2,可以计算出宽度之比α=0.793 7,长度之比β= 0.707 1。
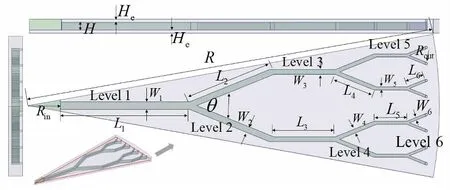
(a) TMCHS

表1 TMCHS的具体尺寸Tab.1 Dimensions of the TMCHS
1.2 控制方程及边界条件
为了使计算模型更简单、更合理,提出了以下几个假设:(1)流动为定常层流;(2)流体是不可压缩、黏性牛顿流体;(3)粗糙表面上无滑移速度和温度;(4)所有固体边界上的温度和热流连续。
质量方程:
∇·v=0
(3)
式中:v为流体的速度矢量;∇为哈密顿算子。
动量方程:
ρf(v·∇)v=μ∇2v-∇p
(4)
式中:ρf为流体密度,kg·m-3μf为流体的动力黏度,N·s·m-2;p为流体压强,Pa;∇2为拉普拉斯算子。
对流体,能量方程:
ρfCp,f(v·ΔT)=λfΔ2Tf
(5)
式中:Cp为流体的比定压热容,J·kg-1·K-1;Tf为流体的温度,K;λf为流体热导率,W·m-1·K-1。
对固体,能量方程:
λsΔ2Ts=0
(6)
式中:λs为固体热导率,W·m-1·K-1;Ts为流体的温度,K。
本文采用有限体积法对TMCHS中的流体流动和传热进行了数值模拟。固体采用硅,具体物性参数如下:密度为2 328.3 kg·m-3,比定压热容为700 J·kg-1·K-1,导热系数为148 W·m-1·K-1。工作流体为水,具体物性参数如下:密度为1 000 kg·m-3,动力黏度为8.55×10-4N·s·m-2,比定压热容为4 179 J·kg-1·K-1,导热系数为0.613 W·m-1·K-1[20]。入口设置为速度入口,入口温度保持在298.15 K,出口均设置为压力出口。在TMCHS的底部施加恒定热流密度Q=100 kW·m-2的热源,并假定顶部边界和侧壁边界是绝热的。沿半径方向的两侧壁面采用周期性对称边界。数值模拟采用SIMPLE算法求解,动量方程和能量守恒方程采用二阶迎风差分格式。当质量方程的归一化残差小于10-6,能量方程的归一化残差小于10-8,底部温度不再变化时,认为计算精度达到收敛。
1.3 模型及网格无关性验证
为了验证结果的合理性,将出口上升温度的数值模拟结果与理论结果进行比较,还与文献[10]的实验结果进行了对比。出口上的升温度随不同平均雷诺数Reave的变化关系如图3(a)所示,明显可以看出模拟值随着雷诺数的增大越接近理论值。与文献[10]对比的结果如图3(b)所示,也能看出模拟结果与实验结果非常接近。因此,验证了数值结果的合理性和有效性。理论出口上升温度的计算方法[21]如下:

Reave/103(a)
(7)
式中:Tout为出口温度,K;Tin为进口温度,K;Cp为流体的比定压热容,J·kg-1·K-1;m为质量流量,kg·s-1;Q为热源提供的热量,J。
为了减少计算误差并提高计算精度,流体域的网格加密,流体域壁面处再次加密。本文设置了3种不同网格数量的非结构网格,网格数分别为319万、494万、940万。网格数为494万的示意图如图4。在Reave为120的条件下进行了网格无关性验证,以网格数最多的压降Δp和出口上升温度ΔT作为衡量标准,得到如表2所示结果,当网格数量为319万时,Δp的误差Ep为0.09%,ΔT的误差ET为0.38%;当网格数量为494万时,Δp的Ep为0.05%,ΔT的ET为0.12%。由于网格数量为494万的误差最小,所以本文的数值模拟网格采用网格数量为494万的设置方法。
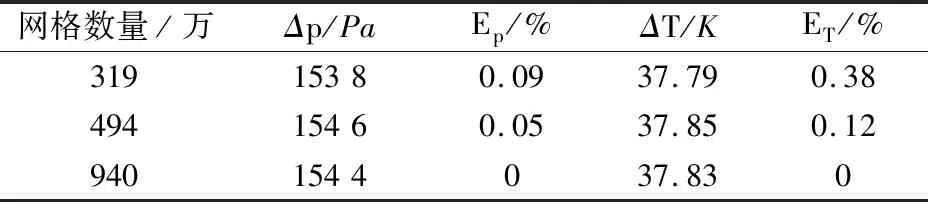
表2 网格无关性表Tab.2 Grid Irrelevance Table

图4 网格示意图Fig.4 Schematic diagram of the grid
1.4 数据处理
(1)雷诺数。
雷诺数是一种可用来表征流体流动情况的无量纲数,表示惯性力和黏性力的比值。一般采用进口的雷诺数来评价尺寸一致的微通道的流动特性,采用平均雷诺数评价尺寸不一致的微通道的流动特性。树状微通道尺寸差异较大,因此采用平均雷诺数作为评价依据,定义如下:
(8)
式中:ρf为流体密度,kg·m-3;vave为微通道流体的平均速度,m·s-1;Dave为微通道的平均水力直径;μf为流体的动力黏度,N·s·m-2。
微通道流体平均速度计算公式如下:
(9)
平均水力直径计算公式[13]如下:
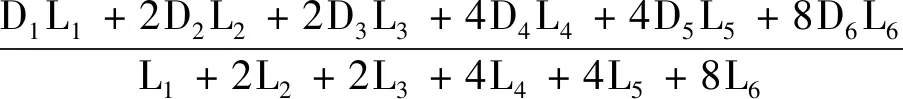
(10)
(11)
式中:Wi为各级微通道宽度;i为微通道级数。
(2)对流换热系数。
本文采用平均对流换热系数have,计算公式如下:
(12)
(13)
A=2(W1+H)L1+4(W2+H)L2+4(W3+H)L3+
8(W4+H)L4+8(W5+H)L5+16(W6+H)L6
(14)
式中:Q为TMCSH热源提供的热量,J;R为TMCSH的半径,m;q为热源的热流密度,W·m-2;A为流道和固体接触的面积,m2;Ts,ave为固体域的平均温度;Tf,ave为流体域的平均温度,K。
(3)平均努塞尔数。
努塞尔数Nu是在流体边界的热传递中跨越边界的对流热量与传导热量的比率,表征换热的强度,本文采用平均努塞尔数Nuave,其计算公式如下:
(15)
式中:have为平均对流换热系数;Dave为微通道的平均水力直径;λf为流体热导率,W·m-1·K-1。
固体平均温度Ts,ave和流体平均温度Tf,ave,计算方法如下:
(16)
(17)
(4)阻力损失。
在评价TMCHS的综合性能时,不仅要考虑其传热特性,还要考虑微通道流道的阻力损失。在本研究中,阻力损失由总压降代替,计算方法如下:
Δp=pin-pout
(18)
式中:pin为进口的总压,Pa;pout为出口的总压,Pa。
(5)整体性能系数。
通常微通道流动传热Nu和压降的变化呈非线性相关,Nu随压降非线性增长,压降的数量级要高于Nu,为了更加准确地评价换热与压力损失,采用整体性能系数η来评判热交换系统的热力性能及水力性能。在本文的分析中,η大于1说明是正优化,换热能力更强;η越大,则换热性能越强。η计算方法[13]如下:
(19)
式中:下标0表示未进行结构优化的TMCHS模型。
2 结果讨论
为了强化换热,本文研究了不同微通道的宽W和不同微通道的高H,具体尺寸见表3。再引入流动干扰技术(在侧壁加入半圆和三角形的空腔)来达到强化换热的目的。通过对比分析TMCHS的流动、传热,压降特性,以及整体性能系数,得到换热性能最佳的散热器。

表3 本文研究的不同微通道的宽和高Tab.3 Different microchannel widths and heights studied in the present work
2.1 流动特性分析
在以对流换热为主要换热机制的散热器中,流体流动特性对换热和压降影响很大。当Reave=200,X从0.010 m到0.016 m时,微通道中间水平截面的速度和流线分布如图5所示。对于TMCHS(图5(a)、图5(b)),可以观察到流体的最大速度出现在通道中心,最小速度出现在通道外侧壁附近。当流体流入分支通道时,最大速度向通道内壁移动,在通道外壁附近出现停滞区,这将导致通道内壁附近的换热性能较高,通道外壁附近的换热性能较低。对于TMCHS-C(图5(c)),可以看到空腔产生二次流,导致流体边界层的不断破坏和再生,从而不断地将边界热量带入主流,从而强化对流换热。空腔的加入扩大了外壁附近的滞流区,进一步强化了内壁附近的换热,削弱了外壁附近的换热。与TMCHS-C相比,TMCHS-T(图5(d))的扰动较小,因此传热相对较低。
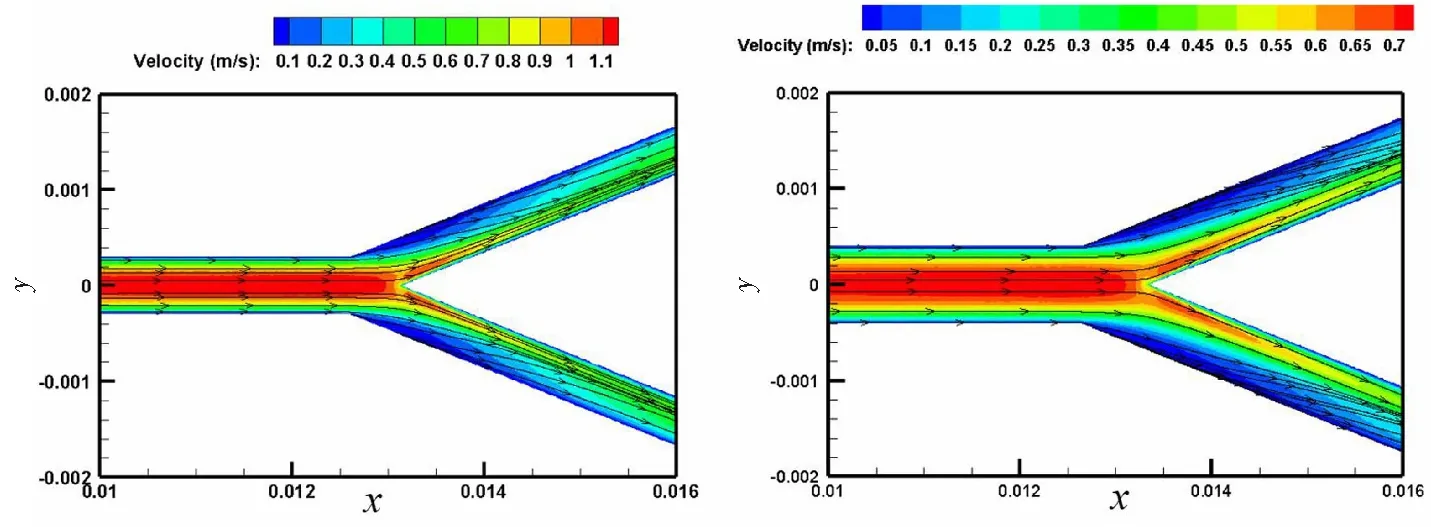
(a) TMCHS(W1=0.8,H=0.5) (b) TMCHS(W1=0.8,H=0.9)
2.2 传热特性分析
TMCHS的最高温度和温度分布情况是评价TMCHS传热特性的重要指标。当Reave=200时,4种不同结构的TMCH加热面的温度分布如图6所示。从图6(a)可以看出,TMCHS(W1=0.6,H=0.5)的最高温度为328 K,图6(b)中TMHS(W1=0.8,H=0.9)的最高温度为320 K。并且通过改变不同TMCHS的宽W和高H,可以将加热面的最高温度降低8 K,从而极大地提高了传热性能。在侧壁加入三角形(图7(c))和半圆空腔((d))的TMCHS的温度分布明显比没有空腔(图6(a)、(b))时均匀得多。此外,半圆形空腔的高温区域最小,三角形空腔次之,无空腔的最大。
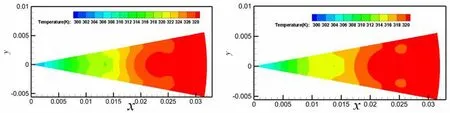
(a) TMCHS(W1=0.6,H=0.5) (b) TMCHS(W1=0.8,H=0.9)
图7展示了4种不同结构的TMCHS中间水平截面上的温度分布,可以直观地看到4种TMCHS的温度沿X方向分层分布。当X=0.02时,从L3开始出现高温集中区域。随着流动的进行,来自TMCHS的所有热量都由流体沿着出口的方向传递。TMCHS(W1=0.6,H=0.5)的高温区最大,集中在L3以后的区域。TMCHS-C(W1=0.8,H=0.9)具有最小的高温区域,集中在L3、L4和L5的中心线附近。TMCHS-T(W1=0.8,H=0.9)的高温区域小于TMCHS-C(W1=0.8,H=0.9),后者集中在L3、L4、L5和L6的中心线附近。中部水平截面表现出和加热面相同的温度分布,进一步说明了强化换热的效果显著。
散热性能最直接的体现就是最高温度的变化,这一点可以通过计算相应的参数,由具体数值体现。图8给出了不同结构的TMCHS的Nuave随Reave
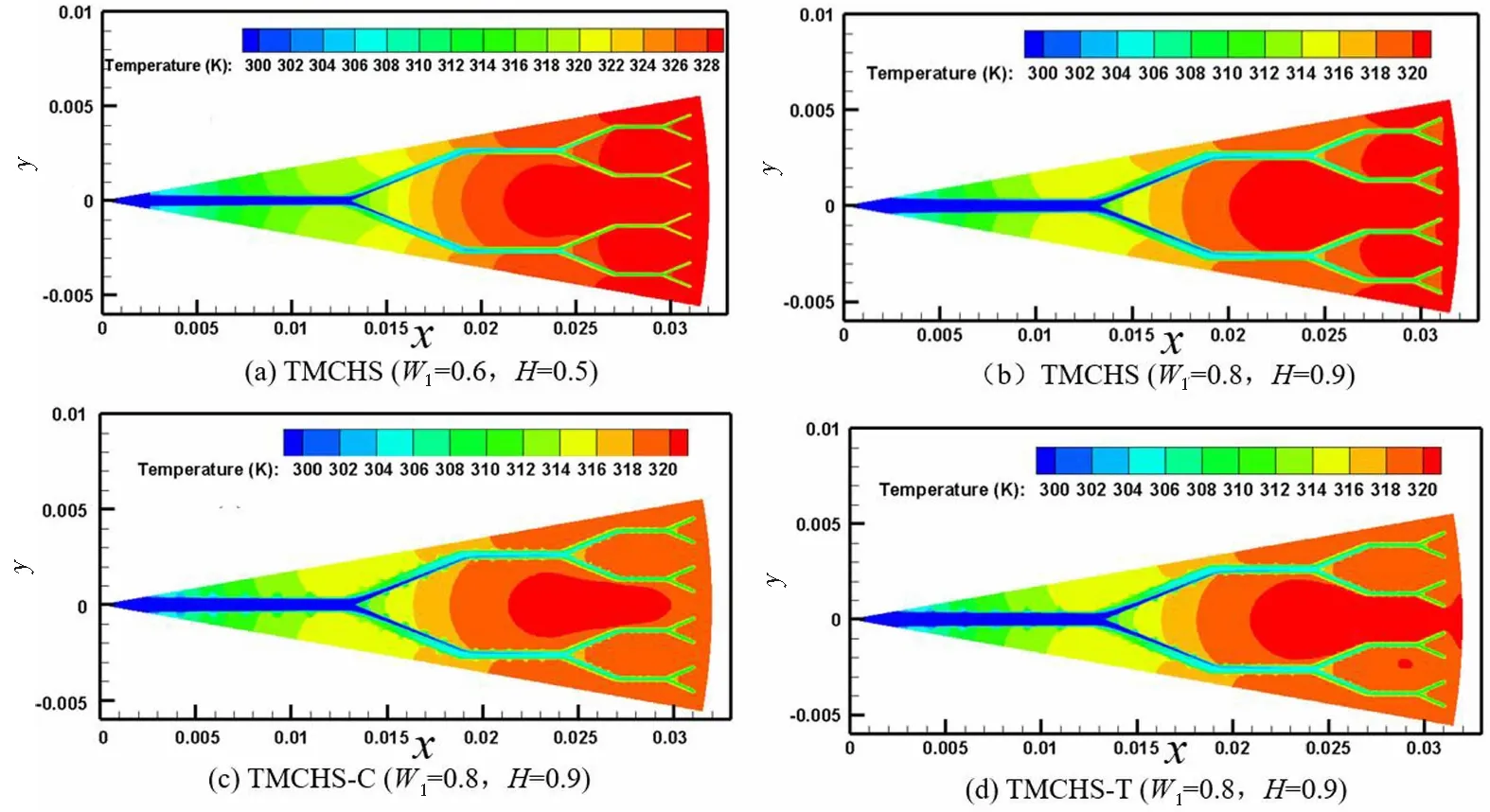
图7 当Reave=200时,TMCHS中间水平截面的温度分布Fig.7 Temperature distributions in the middle cross horizontal section of TMCHS at Reave=200
的变化情况。如图8(a)所示,当Reave相同时,TMCHS的Nuave随Reave的增大而增大;当H为常数时,TMCHS的Nuave随Reave的增大而增大;说明TMCHS的换热性能随H的增大而提高。由于在H=0.9时TMCHS具有最高的整体性能系数η,因此选择H=0.9作为基准来研究具有不同W的TMCHS对整体性能的影响。如图8(b)所示,在Reave不变时,TMCHS的换热性能随W的增大而增大,A变大,使得对流换热加强。在W一定的情况下,TMCHS的Nuave随Reave的增大而增大。TMCHS-C和TMCHS-T的Nuave明显大于TMCHS。综上所述,TMCHS-C(H=0.9,W1=0.8)的高温区域最小,温度分布最均匀,传热性能最好。换热性能强弱排序为:TMCHS-C>TMCHS-T>TMCHS,再次说明了本文强化换热的可行性。
2.3 压降性能分析
在Reave=200时,不同结构的TMCHS在中间水平截面的压力分布如图9所示。由于通道中的阻力损失,压力不断降低。从图9(a)、(b)可以看出,在分支节点的内侧壁处出现了很大的压力,这是由于微通道的速度突然降低所造成的。在相同尺寸下,小尺寸微通道的流速较大,因此v是影响Δp的主要因素,A是次要因素。如图9(c)、(d)所示,在侧壁加入半圆和三角形空腔后,在主流道中存在收缩效应,导致压力梯度倒置。从压力云图的色带前移可以看出,二次流的产生会将空腔内的流固阻力变为流液阻力,从而降低Δp。在TMCHS的侧壁加入空腔导致微通道内的压力分布更加不均匀,内侧壁附近的压力较大,外侧壁附近的压力较小,这种不均匀的压力分布增大了Δp,TMCHS-C压力分布最不均匀。

Reave/103(a)

(a) TMCHS(W1=0.6,H=0.5) (b) TMCHS(W1=0.8,H=0.9)
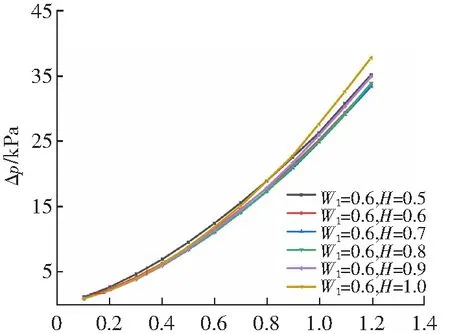
不同结构TMCHS的Δp和Reave的关系如图10所示。TMCHS所有的Δp都随着Reave的增加而增加,Reave越大对应的v越大,对应的阻力损失越大。图10(a)表明了在W不变,Reave>900时,随着H的变化,Δp变化较大,且当H=1.0时最大,H=0.8时最小;当Reave<900时,随着H变化,Δp变化很小,且当H=0.5时最大,H=0.8时最小。在相同的小Reave下,速度是影响Δp的主要因素,A对Δp的影响是次要因素。随着Reave的增加,A对Δp的影响是主要因素。Reave=900是一个转折点,TMCHS(W1=0.6,H=1)这一结构最为明显,当Reave>900时表现为最大的Δp。图10(b)表明了在H=0.9时,W越大Δp越小。此时,对Δp起主要作用的是速度,所以TMCHS尺寸越大Δp越小。图10(c)表明了加入空腔必然会增加扰动进而增加Δp,其中半圆空腔的Δp最大,其次是三角形空腔,不加空腔的直流道的Δp最小。虽然加入空腔会增加Δp,但是空腔内形成的二次流能降低部分Δp。综合比较下来,直流道和加入空腔的流道Δp差异不大。
2.4 综合性能分析
为了综合分析换热和压降特性,采用综合性能系数η来评判热交换系统的热力性能及水力性能。如图11(a)所示,当Reave<900时,随着Reave的增加η减小,说明随着Reave的增加,增加的换热性能对综合性能的影响要小于Δp;当Reave>900时,随着Reave的增加η出现波动,说明此时TMCHS受到两者的影响。TMCHS(W1=0.6,H=0.9)的平均η最大,并且η>1,说明都是正优化。如图11(b)所示,TMCHS(W1=0.5,H=0.9)的η<1,是负优化;TMCHS(W1=0.7,H=0.9)和TMCHS(W1=0.8,H=0.9)η>1,都是正优化,其中TMCHS(W1=0.8,H=0.9)的η最大,皆在1.4左右徘徊。因此选取TMCHS(W1=0.8,H=0.9)作为研究空腔对微通道换热性能影响的直流道。如图11(c)所示,在侧壁加入半圆、三角形空腔的TMCHS在Reave>300时,就能实现正优化,最大值在1.1左右。Reave<1 000时,η随着Reave的增加而增加。这是因为Reave越大,v越大,二次流强度越强,从而增加了传热。此时对TMCHS综合性能影响最大的是其换热能力。当Reave>1 000时,影响综合性能的主要因素是Δp,进而强化因子η开始减小。其中TMCHS-C(W1=0.8,H=0.9)是综合性能最好的散热器(η最大)。
Reave/103(a)

Reave/103(a)
3 结论
(1)树状微通道分支结构使流体的最大速度位置向内壁移动,在外壁附近留下滞流区,导致内侧壁面附近换热性能较高,外侧附壁面近换热性能较低。
(2)TMCHS(W1=0.8,H=0.9)是改变结构得到综合性能最好的散热器,使加热面的最高温度下降了8 K。
(3)在TMCHS(W1=0.8,H=0.9)的侧壁加入空腔,促进了微通道中二次流的产生,导致了流动和热边界层的持续破坏和再生,有效地提高了换热性能,让加热面的高温区域面积明显减小,温度分布更均匀。
(4)TMCHS-C相比于TMCHS-T,具有更高的换热性能,更均匀的温度分布,但也表现出更高的压降。

