基于500 MPa钢筋的高强套筒灌浆连接力学性能
刘鑫宇,曾思智,2,*,朱春晖,胡淑军,梁文沁
(1.南昌大学工程建设学院,江西 南昌 3300312.江西中煤建设集团有限公司,江西 南昌 3300013.赣州建筑工业化有限公司,江西 赣州 341007;4.天津大学建筑工程学院,天津 300350)
套筒灌浆连接主要应用于装配式混凝土结构中预制构件的连接中,主要通过灌浆料填充在钢筋和灌浆套筒之间,并由此形成可靠的连接形式,以实现装配式结构等同于现浇结构的要求[1]。当前灌浆套筒连接中主要采用HRB400级钢筋,存在强度偏低、配筋率大、构造复杂、用钢量大和施工难度高等问题[2-3]。许多学者建议采用强度更高等级的钢筋。
李锐等[4]对配置500 MPa钢筋的预制混凝土柱进行研究,其承载力与现浇柱相近,且极限位移角可达1/31;赵勇等[5]对受力纵筋为500 MPa、直径为25 mm和36 mm,且灌浆料强度为97 MPa的预制混凝土柱进行研究,出现了纵筋从套筒中拔出的现象,即套筒灌浆连接承载力不足;高向玲等[6]通过对HRB400、HRB500和HRB600级钢筋力学性能进行分析,得到了灌浆料强度为80 MPa时不同级别钢筋在灌浆套筒内的锚固长度;戎贤等[7]对采用HRB600级的装配式混凝土框架节点进行试验研究,发现具有良好耗能、承载和变形能力,并可解决节点区配筋密集和混凝土浇筑困难等问题;戢文占等[8]通过优化配合比设计了一种抗压强度超过120 MPa的灌浆料,可与高强钢筋在套筒灌浆连接中共同使用。另外,郑永峰等[9]指出,套筒环肋数量是影响套筒灌浆连接的重要因素之一。
本文首先对套筒灌浆连接的受力原理进行详细分析,随后基于500 MPa级、直径为16 mm钢筋和高强灌浆料(≥80 MPa),设计多组考虑套筒厚度、钢筋锚固长度、套筒环肋数量和灌浆料强度的高强套筒灌浆连接模型,并采用校正的有限元法研究各模型的力学性能,以及提出设计建议,从而使基于500 MPa钢筋的高强套筒灌浆连接具有可靠连接性能,为其在装配式混凝土结构中的应用提供理论基础。
1 套筒灌浆连接的承载力分析
在单向拉向、高应力反复拉压和大变形反复拉下作用下,套筒灌浆连接的破坏模式主要包括钢筋在套筒外断裂、套筒筒体断裂、钢筋与灌浆料黏结滑移破坏(钢筋刮犁式拔出)和套筒与灌浆料黏结滑移破坏(灌浆料刮犁式拔出)4种形式[6]。其中,钢筋在套筒外断裂属于理想的延性破坏,故需有效防止其他3种破坏形式。
1.1 套筒灌浆连接接头的受力原理
如图1所示,在外力作用下,套筒灌浆连接接头主要受到机械咬合力、摩阻力和胶结力的作用。当钢筋受力时,灌浆套筒内的灌浆料和钢筋、灌浆料和套筒之间均会产生斜向挤压力,且该挤压力可分解为垂直钢筋的径向分力和平行于钢筋的轴向分力。其中,径向分力主要约束灌浆料的劈裂膨胀变形,轴向分力限制灌浆料滑移。因此,连接中需保证各构件之间具有足够承载力。
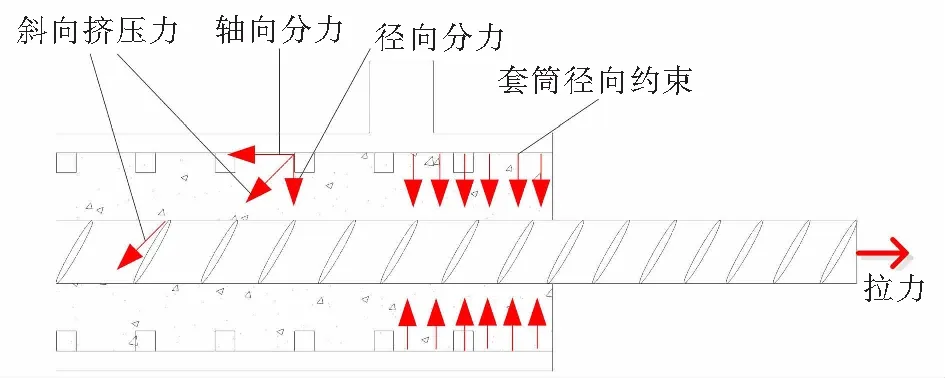
图1 套筒灌浆连接受力图Fig.1 Schematic diagram of sleeve grouting connection
1.2 钢筋和灌浆料的黏结理论
根据Henin等[10]提出的套筒灌浆连接中钢筋的锚固长度l计算公式,具体表示为:
(1)
式中:Psy为钢筋屈服力;d为钢筋直径;fb为钢筋表面的黏结应力。
依据剪切摩擦理论,钢筋和灌浆料的黏结应力为钢筋表面径向约束力fn与钢筋和灌浆料表面摩擦系数μ的乘积[10],具体表示为:
fb=fn×μ
(2)
以钢筋屈服为临界状态计算套筒临界锚固长度,钢筋表面径向约束力fn[11]可表示为:
fnd=2t1Tsl,y
(3)
(4)
式中:t1为套筒壁厚;Tsl,y为套筒屈服应力;fm为灌浆料抗压强度。
1.3 套筒和灌浆料的黏结理论
套筒变形段对灌浆料的黏结力Ps,2主要由摩擦力Ps,f和机械咬合力Ps,zi组成。黏结力Ps,2具体可由式(5)和式(6)表示[12]:
(5)
(6)
式中:μ为套筒与灌浆料间的摩擦系数;Ps,2r为环肋径向分力所产生的约束力;Ds,in为套筒内径与肋高之差;hr为环肋高,L为变形段长度;n为套筒内的环肋数量。
1.4 套筒的受力分析
套筒灌浆连接中,试件抗拉强度与连接钢筋抗拉强度标准值的比值不小于1.10,且所有接头需满足《钢筋机械连接技术规程》[13]中Ⅰ级接头强度要求,具体表示为:
fmst×A≥1.1×fstk×As
(7)
式中:fmst为套筒抗拉强度;fstk为钢筋抗拉强度标准值;A为套筒横截面积;As为钢筋面积。
2 有限元分析方法与校正
2.1 材料参数
(1)灌浆料。
采用某种灌浆料拌和物制作3个40 mm× 40 mm×160 mm试件,并在养护28 d后进行抗压性能试验研究,其抗压强度值分别为122.36,122.61和129.71 MPa,平均值为124.89 MPa。有限元分析时,灌浆料的应力-应变曲线采用丁发兴-余志武高强混凝土本构关系[14]。
(2)钢筋和套筒。
选取3根直径为16 mm的500 MPa级钢筋作为试样,并进行材性试验,以得到相应屈服强度、抗拉强度;套筒的材料性能按《钢筋连接用灌浆套筒》[15]取值,材性如表1所示。

表1 钢筋和套筒的力学参数Tab.1 Mechanical parameters for reinforcement and sleeve
2.2 有限元分析方法
(1)求解方法。
在ABAQUS/Standard模块中,选择迭代式线性方程求解法解决高强灌浆套筒的非线性问题,可使数值结果更为精确。
(2)单元选取与网格划分。
采用ABAQUS软件建立有限元模型,且由于模型对称性,仅建立采用1/2模型,如图2所示。套筒、灌浆料和钢筋均采用C3D8R单元。分析模型中,套筒和灌浆料的网格大小为5 mm,高强连接钢筋的网格划分大小为3.6 mm。

图2 分析模型Fig.2 Analytical model
(3)单元接触。
有限元模型中,套筒与灌浆料之间具有良好的黏结性能,故两者间的接触设置为绑定;灌浆料和钢筋采用接触设置,其中法向采用“硬接触”,切向摩擦系数定义为0.54[16]。
(4)边界条件和加载方式。
① 边界条件。如图3所示,在套筒灌浆连接两端钢筋的正截面处各选取一个参考点,并将端面上所有节点自由度全部耦合于该参考点。同时,在一端参考点上施加“完全固定”边界条件,即约束端面上所有自由度;另一端参考点上施加Z方向(沿套筒长度方向)位移。

图3 边界条件Fig.3 Boundary condition
② 加载方式。为准确模拟套筒灌浆连接在单向拉伸下的力学性能,采用位移加载的方式,加载速率为1 mm·s-1[2],即在ABAQUS有限元软件中创建等间距型幅值,并输入幅值与相对应的时间参数来实现加载速率的赋值。
(5)材料本构关系。
本文钢筋和套筒本构模型均选用双折线模型[17],即钢筋屈服后有一定强化能力。灌浆料弹性模量取38 000 MPa,泊松比取0.2。考虑塑性损伤本构的应力-应变曲线[17],损伤塑性参数包括膨胀角、偏心率、双轴受压与单轴受拉极限强之比fb0/fc0、受拉子午线与受压子午线常应力的比K和黏滞参数,分别取值30,0.1,1.16,0.667和0.005[18]。
2.3 有限元分析校正
(1)分析模型。
高强等[2]对堆焊成型套筒灌浆连接性能进行试验研究,选取试件A-5d、A-6d与A-7d进行有限元模拟校正。试件A-6d的连接钢筋为直径25 mm、HRB400E级钢筋,其屈服强度和抗拉强度分别为429 MPa和625 MPa;钢筋伸入灌浆料内的锚固长度为6倍钢筋直径d;灌浆料抗压强度平均值为95.2 MPa;灌浆套筒壁厚为5 mm,剪力槽尺寸为底宽3 mm、高1.5 mm,剪力槽间距为25 mm,套筒外径为57 mm,套筒总长度340 mm。有限元模型建立时,单元选取、网格划分、接触设置、边界条件和加载方式均与2.2节相同。
(2)分析结果。
试件A-5d、A-6d与A-7d与有限元模型B-5d、B-6d和B-7d的力-位移曲线如图4(a)所示。弹性阶段,各曲线的弹性刚度、荷载和位移基本相同,弹性极值处所对应荷载值分别为179.68,175.30,176.32,168.22,165.36,166.96 kN。荷载继续增大且钢筋进入弹塑性后,极限荷载分别为227.42,240.10,241.32,238.52,236.99,236.23 kN,且曲线走势基本相同。对比图4(b)试验与有限元的破坏模式,两者破坏均发生在套筒外钢筋处,与预期相符。
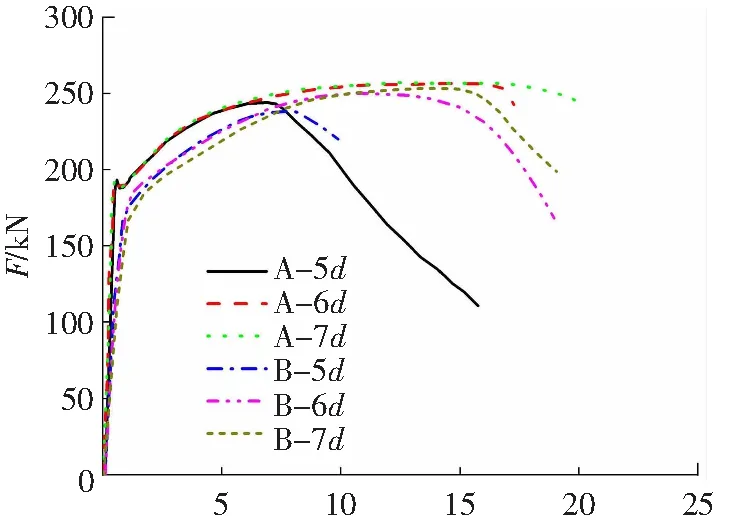
X/mm(a) 力-位移曲线

(b) 破坏模式图4 有限元与试验分析结果对比Fig.4 Comparison of test and FE results
基于对比上述试验与有限元分析所得力-位移曲线和破坏模式可知,2.2节中的有限元法可用于套筒灌浆连接力学性能的分析中。
3 高强套筒灌浆连接的力学性能
3.1 模型设计
为考虑套筒厚度、锚固长度、环肋数量和灌浆料强度对高强套筒灌浆连接力学性能的影响,基于HRB500级、直径为16 mm的受力钢筋,并结合1.2节~1.4节中对各构件的承载力分析,设计4组共17个有限元模型。其中,套筒总长为340 mm,单个环肋的高度和宽度均为3 mm[15]。如表2,模型参数具体描述如下:
(1)套筒厚度。试件A1~A5锚固长度、环肋数量和灌浆料强度分别为8d、12个和120 MPa,套筒厚度分别为2,3,4,5,6 mm。

表2 有限元模型参数Tab.2 Parameters of FE models
(2)锚固长度。试件A4、A6~A9环肋数量、灌浆料强度和套筒厚度分别为12个、120 MPa和5 mm,锚固长度分别为8d、5d、6d、7d、9d。
(3)环肋数量。试件A4、A10~A13锚固长度、灌浆料强度和套筒厚度分别为8d、120 MPa和5 mm,环肋数量分别为12个、20个、16个、8个、6个。
(4)灌浆料强度。试件A4、A14~A17的锚固长度、环肋数量和套筒厚度分别为8d、12个和5 mm,灌浆料强度分别为120,80,90,100,110 MPa。
3.2 破坏模式
结合2.1节材料参数和2.2节分析方法,对所设计的17个模型进行有限元建模分析,可得到相应屈服荷载fsy、屈服位移Δy、极限荷载fsu、极限位移Δu和破坏模式等,具体如表3所示。
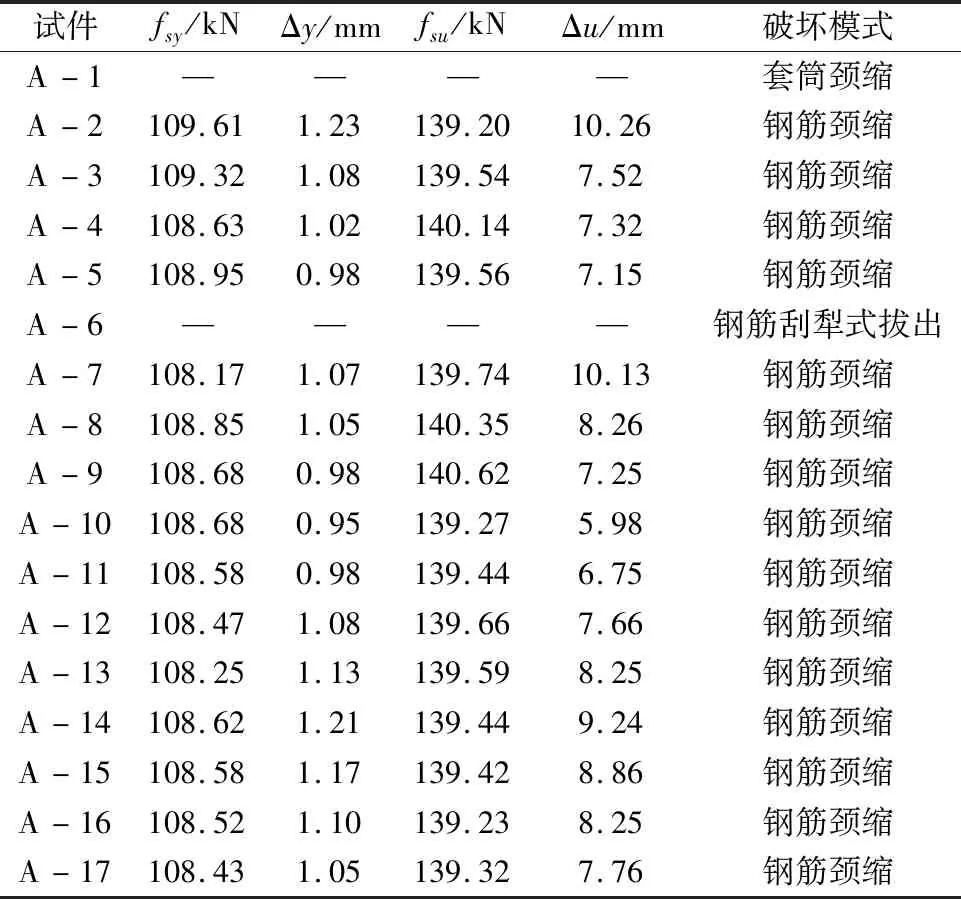
表3 破坏模式Tab.3 Failure modes
3.3 套筒厚度
基于式(7)可知,套筒厚度需大于2.3 mm才能满足Ⅰ级接头强度要求。图5为试件A1~A5的力-位移曲线图。结合表可知,试件A1套筒厚度仅有2 mm,不满足接头强度要求,故套筒发生颈缩现象并导致连接提前破坏,承载力仅为90.68 kN;试件A2~A5均发生钢筋断裂,且极限荷载基本相同,但A2的极限位移明显大于其他3个试件,这主要是由于套筒面积不足引起了套筒和相应连接的较大塑性变形。
图6为试件A1~A5的套筒应力云图。各试件最大应力均发生在套筒中部,且最大力值分别为601.5,474.9,276.4,244.1,172.2 MPa。其中,试件A1套筒最大应力值已超其抗拉强度,故套筒发生颈缩;其余试件套筒应力均随壁厚的增加而减小,且厚度超过4 mm后最大应力值和最大应力区域均变化较小。因此,设计时建议取值为4 mm,即套筒厚度需比计算厚度值增大1 mm以上。

X/mm图5 考虑套筒厚度的力-位移曲线Fig.5 Force-displacement curve with sleeve thicknesses
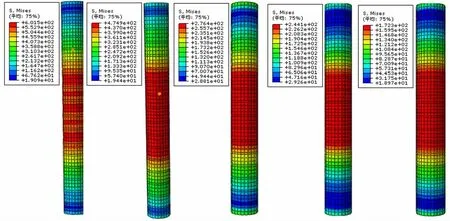
(a)A1 (b)A2 (c)A3 (d)A4 (e)A5
3.4 锚固长度
对于不同锚固长度,当灌浆料强度为120 MPa,套筒厚度为5 mm,套筒屈服应力为350 MPa时,fn取式(4)中的较小值0.2fm。结合式(1)~式(4),可得出高强灌浆套筒钢筋临界锚固长度计算方法,具体表示为:
(8)
基于式(8)可知,基于120 MPa灌浆料的钢筋的最小锚固长度为5.88倍的钢筋直径d。
图7是考虑锚固长度时试件A4、A6~A9的力-位移曲线。由于试件A6中钢筋锚固长度仅为5d且小于最小锚固长度,在荷载仅为86.72 kN时发生了钢筋刮犁式拔出。试件A4、A7~A9均发生钢筋断裂。随着锚固长度的增大,各试件屈服荷载和极限荷载无明显影响,但屈服位移略微减小;试件A7的极限位移为10.13 mm,明显大于其他试件的极限位移,这主要是由于锚固长度为6d时灌浆料与钢筋之间的切向咬合力较小,使得钢筋与灌浆料发生了一定的塑性变形。
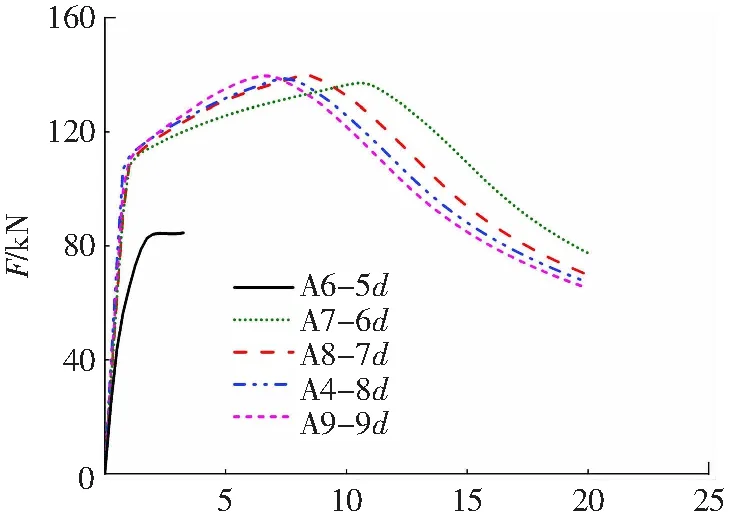
X/mm图7 考虑锚固长度的力-位移曲线Fig.7 Force-displacement curve with anchorage lengths
图8为考虑锚固长度时试件A4、A6~A9中灌浆料的损伤图。各试件中灌浆料的最大损伤位置均处于套筒端部与钢筋连接处。试件A6中钢筋锚固长度较小,端部灌浆料发生明显变形。尽管试件A7的锚固长度大于设计值,但钢筋与灌浆料连接处的灌浆料损伤均较为明显。随着锚固长度继续增大,试件A8、A4和A9中灌浆料损伤区域逐渐较小,均只发生在端口连接处。因此,增大钢筋锚固长度可明显减小灌浆料的损伤。

(a) A6 (b) A7 (c) A8 (d) A4 (e) A9
图9是考虑锚固长度时试件A4、A6~A9中套筒的应力云图,最大应力均发生在套筒中部,并向两端逐渐减小。试件A6中套筒最大应力为53.67 MPa,远小于套筒屈服强度,主要由钢筋刮犁式拔出所引起。试件A7、A8、A4、A9中套筒最大应力分别为213.9,212.3,209.8,211.0 MPa。另外,由于钢筋与灌浆料的作用面积增大,套筒最大应力分布范围在锚固长度增大后有一定减小,但当预埋长度大于7d后,套筒应力分布影响逐渐较小,受力更均匀。

(a) A6 (b) A7 (c) A8 (d) A4 (e) A9
图10是试件A4、A6~A9中一侧的钢筋应力云图。除试件A6发生钢筋刮犁式拔出,且未发生钢筋颈缩破坏外,其余试件的最大应力均为750 MPa,且最大应力处均处于锚固长度外,即钢筋的拉断发生在套筒外侧,与预期相符。

(a) A6 (b) A7 (c) A8 (d) A4 (e) A9
3.5 环肋数量
图11是考虑环肋数量时试件A10、A11、A4、A12、A13的力-位移曲线。结合表可知,由于各试件破坏模式均为钢筋颈缩,相应的力-位移曲线走势相同,均包括弹性和弹塑性状态,且在达到极限状态后曲线呈下降趋势。各试件的屈服荷载和极限荷载基本相同,主要取决于钢筋的屈服强度和极限强度。然而,当环肋数量从20个减小至6个时,屈服位移由0.95 mm增大至1.13 mm,极限位移由5.98 mm增大至8.25 mm。这主要由于套筒环肋产生的横向分力和滑移约束逐渐减小,导致套筒对灌浆料的黏结作用减弱和滑移增大,从而引起屈服、极限位移随环肋个数减小而增大,与式(6)计算结果相符。

X/mm图11 考虑环肋数量的力-位移曲线Fig.11 Force-displacement curves with ring numbers
为进一步了解灌浆料与套筒之间的滑移能力,取试件A10~A11、A4、A12、A13在考虑环肋数量时沿套筒长度方向的位移云图,如图12所示。各模型中最大滑移均位移端口位置处,滑移值分别为3.38,3.74,3.87,3.89,4.36 mm。灌浆料整体滑移随着环肋数量的减小而增大,即套筒的环肋数量的增加能够有效阻止灌浆料的滑移,与力-位移曲线中的走势相同。

(a) A10 (b) A11 (c) A4 (d) A12 (e) A13
图13是考虑环肋数量下试件A10~A11、A4、A12、A13中套筒的应力云图。随着环肋数量的增大,各试件中套筒的最大应力均位于套筒中间,且最大应力值和应力区域基本相同,即环肋数量对套筒应力无明显影响。图14是考虑环肋数量下各试件中钢筋的应力云图,最大应力值均为750 MPa,且最大应力处和发生颈缩断裂处位于锚固长度段以外,与预期相符。综上可知,考虑套筒加工难度,建议环肋数量取8~16个。
3.6 灌浆料强度
图15是考虑灌浆料强度的试件A14~A17、A4的力-位移曲线。结合表可知,各曲线均表现出相同的走势,且破坏模式均为钢筋颈缩破坏。另外,各试件的屈服荷载和极限荷载基本相同,但随着灌浆料强度由C80增大至C120,屈服位移由1.21 mm减小至1.02 mm,极限位移由9.24 mm减小至7.32 mm,即增大灌浆料强度能明显提高连接的强度和减小其塑性变形。

(a) A10 (b) A11 (c) A4 (d) A12 (e) A13

(a) A10 (b) A11 (c) A4 (d) A12 (e) A13
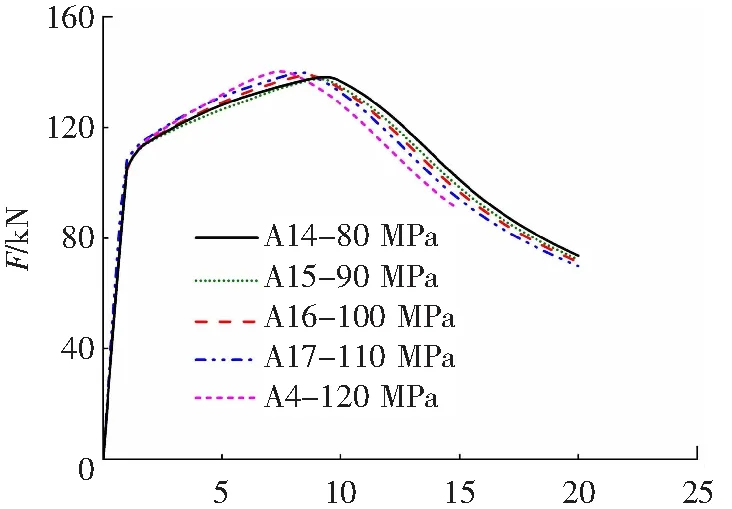
X/mm图15 考虑灌浆料强度的力-位移曲线Fig.15 Force-displacement curve with grouting material strength
图16为考虑灌浆料强度的试件A14~A17、A4中灌浆料损伤图。由于各试件的钢筋锚固长度相同,故灌浆料两端与钢筋连接处的损伤区域相同,且最大损伤值均为0.98。然而,尽管灌浆料的最大损伤位置均处于两端,但随着灌浆料强度的增大,损伤区域内灌浆料的损伤值有明显减小。在灌浆料强度达到120 MPa时,仅有端部较小区域内的损伤值较大,其余与钢筋连接处仍有较大承载力,故设计时建议尽量增大其强度值。

(a) A14 (b) A15 (c) A16 (d) A17 (e) A4
图17是考虑灌浆料强度下试件A14~A17、A4中套筒的应力云图。随着灌浆料强度的增大,各试件中套筒的最大应力区域为套筒中部,并向两端逐渐减小;各试件的最大应变值基本相同,均处于210 MPa左右,小于套筒的屈服强度值,即套筒在不同灌浆料强度下均具有足够承载力。图18是考虑灌浆料强度下试件A14~A17、A4中钢筋的应力云图。各试件中钢筋的最大应力均为750 MPa,发生颈缩断裂处均为外伸断,且应力分布方式相同,与预期相符。
结合上述分析可知,对基于500 MPa钢筋的高强套筒灌浆连接,建议灌浆料强度取120 MPa。

(a) A14 (b) A15(c) A16 (d) A17 (e) A4
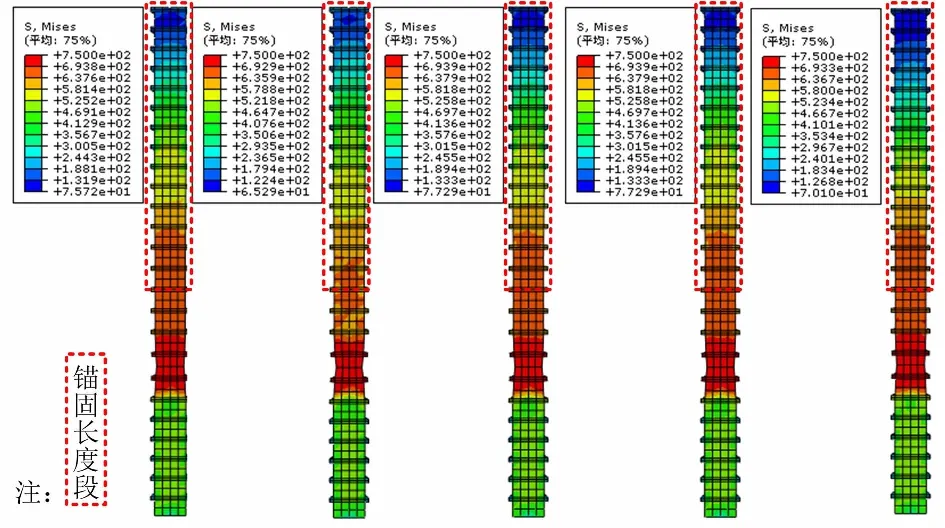
(a) A14 (b) A15(c) A16 (d) A17 (e) A4
4 结论
(1)基于500 MPa钢筋和高强灌浆料的高强套筒灌浆连接具有良好的力学性能,且主要受套筒厚度、锚固长度、环肋数量和灌浆料强度等因素影响,并能出现理想的钢筋断裂破坏;
(2)基于已有的Ⅰ级接头强度理论、钢筋与灌浆料黏结理论分别计算的套筒厚度和钢筋锚固长度均偏小,建议分别取4 mm和7d;
(3)增大环加数量可提高套筒与灌浆料间的黏结作用和减小两者间的滑移,对套筒及破坏模式无明显影响,但考虑加工难度建议取8~16个;
(4)增大灌浆料强度可有效提高连接的强度和减小其塑性变形,以及明显减小损伤区域内灌浆料的损伤,设计时建议灌浆料强度取120 MPa。

