芦原义信街道宽高比(D/H)的栅格计算及应用研究
贾尚宏,邵 万,王姗姗
(安徽建筑大学 建筑与规划学院,安徽 合肥 230022)
尺度问题一直是建筑及规划学者们关注的重要课题。在街道尺度的相关研究中,日本建筑师芦原义信的研究成果影响最为广泛,其著作《街道的美学中》[1]中提出的宽高比(D/H)概念,时至今日已成为街道空间形态测度的经典指标。
尽管宽高比被广泛应用于各种街道尺度的研究中,但出于职业习惯,建筑和规划师们往往更加关注D/H 值带给人们的空间感受[2-4],而对这一几何概念本身缺乏深究的兴趣,以至于它沿用至今,仍没有一个明确的算法定义。同时,目前D/H 值的计算结果依旧停留在单点数值的阶段,横向对比当下主流的空间分析,已然形成点面之间的维度差,由此导致的衔接断裂严重限制了D/H 值研究价值的发挥。
1 当下D/H 值算法的特点
芦原义信在其著作[5]中着力描述了不同宽高比所营造的空间效果,对于D/H 值算法并没有详细解释,书中列举的中华街、元町等例子均抽取了街道两侧平行,沿街建筑等高的理想化的节点(图1),并通过代表性的剖切点,以某一特殊位置的D/H 值描述整条街道的空间特征,是为“近似的近似”。
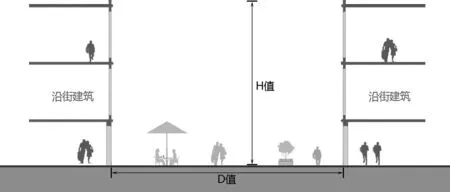
图1 理想化街道节点模型
随着街道形态与尺度研究的逐渐深入,各个国家的学者们都对街道宽高比产生了浓厚的兴趣。美国学者善于从全局视角描述街道的宽高比特征,例如哈维从“街道墙”的概念出发,利用GIS 缓冲区识别近似的街道界面,尝试通过贴线率加权的方法确定街道的总体宽高比[6-7];而其他地区例如中国和奥地利学者则更加倾向于通过分点剖切的方法展开更加细致的研究[8-10]。
其实对于日本或大多数西方国家的街道而言,上述的方法都是适用的,因为他们的街道大体规整,不仅笔直通畅,两侧的体量、造型也整齐划一,简单处理沿街建筑的进退关系,或抽取特征点都足够具有说服力。然而中国人向来喜欢“曲径通幽”,一些传统村落的街巷往往是参差错落,百转千折。面对更加复杂多变的街巷空间,当下的D/H 值算法显得有些难以应对,在实际研究中普遍存在以下几个方面的主要问题:
(1)D 值的不确定性
字面理解,D/H 即是宽度与高度的比值,其中宽度通常指两条平行线间的距离。虽然绝对平行的概念无须较真,但在中国传统村落中,街道两侧不平行且角度较大的情况却相当普遍,此处的宽度该如何定义,或是一个值得商榷的问题。
(2)H 值的不确定性
最早的D/H 值算法抽取了两侧建筑等高的理想化街道模型,回避了两侧不等高的现实情况。在之后的应用研究中,有的学者取平均,有的取最小/最大,更有取单边者,完全隔绝另一侧建筑的尺度影响。这种“自定义”的计算方式虽然能够满足一定条件下的研究需要,但若是涉及与其他要素的联合分析,就会使作为参数的D/H 值本身缺乏客观性和稳定性。
(3)整体的抽象性
以目前的算法,研究者只能通过全局计算整体描述街道的形态特征,或选取有限的代表性节点进行剖切,仍然是“以局部代替整体”的近似方法,虽然能够通过增加测点数量来提高精度,但依旧无法实现对研究区域的全覆盖。
(4)局部的抽象性
目前的算法多以唯一值的形式呈现结果,每处节点空间只有一个结论值,难以描述复杂多变的空间特征。
(5)成果的封闭性
当下对于街巷的宽高比的计算,呈现的结果大多表现为统计表或“剖面+数字”的组合形式。然而相关研究进行到今天,只停留在宽高比本身的表达已远远不够。若能将D/H 值写入通用文件,通过多层面、多参数的联合、对比分析,或能更加深入地挖掘研究对象的潜在属性。换言之,将宽高比作为研究参数而非结果来看待,更能打开研究者们的视野。
2 由点及面的扩展计算方法
可以预见的是,想要将D/H 值作为常态化参数引入更多的横向研究,除了需要保障计算的客观性和准确性以外,还需要在有限的空间内取得充足的样本来反映其变化的趋势。换言之,D/H 计算的结果预期将不再是某个单一的数值,而是一种可以参与空间叠加的二维数组——栅格图。要想实现这一点,新算法就必须借助计算机,并且具备同时计算研究区域内任意点D/H 值的能力。事实上,D/H 于计算机而言不含任何空间意义,仅仅是一个除法公式的结果,因此要实现上述预期,实际上只需确立统一的算法路径判断研究范围内任意一点的D 值和H 值。
2.1 对于D 值
确定D 值的难点在于求解两条不平行线段之间的动态间距。这种模糊的距离概念通常会被拆解为“点到线的距离”或“对应点的距离”。后者显然不切实际,因为识别对应点又是一个将问题复杂化的过程。而寻求“点到线”,势必要通过已知的两条线产生一系列的参考点。此处大致有两种算法(图2):
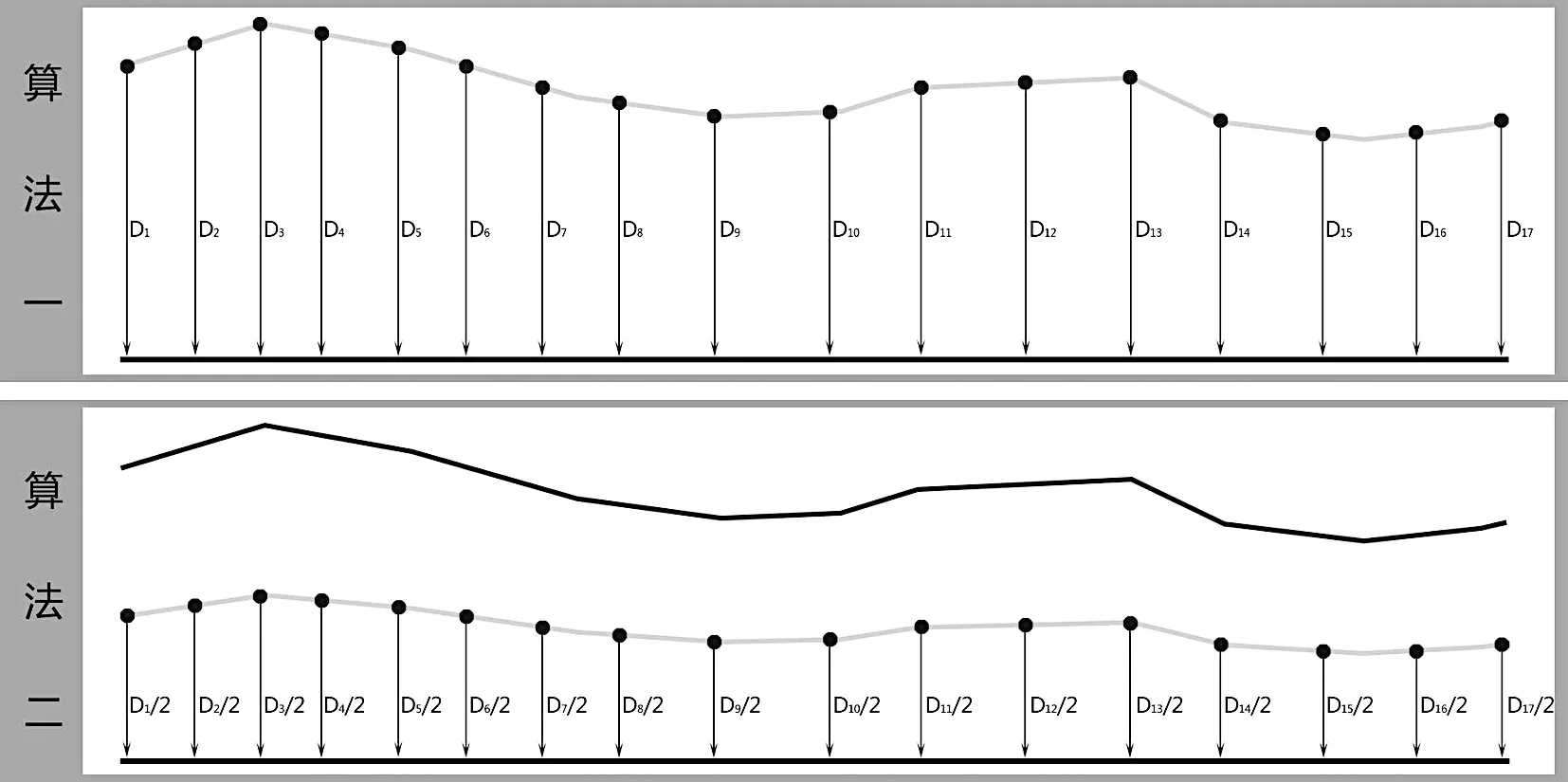
图2 D 值的确定方法
第一种:直接将其中一条线打散成点,由每个点向另一条线引垂线(或切线的垂线),取垂线段长度作为道路间距。该方法简洁明了,便于操作,但在动态对应方面存在误差,仅适用于近似平行或波动不大的街巷空间。
第二种:对于平面中任意一点而言,点到线的距离是最简单易求的。若是将点至街道某一边线的距离记作A,至另一边线的距离记作B,令A=B,筛选出所有符合条件的点,即可得到一条连续的线,也就是通常所说的“道路中心线”。换句话说,中心线上的任意一点均满足“距街道两侧的距离相等”。实际运算中,只要根据精度需求,将中心线打散成点,求这些点距道路任意一边的距离,即可得到D/2 的值。
上述方法仅仅得到了中心线上任意一点的D值,要想实现区域全覆盖的计算还远远不够。因此,必须将D 值由线向面推及,这是一个典型的插值过程。由于中心线可以打散为无数个点,所以算法在中心线水平方向上的精度可以无上限地提高,主要问题集中在垂直方向。为了实现计算需求,此处引入“泰森多边形”的概念[11]。
泰森多边形又称冯洛诺伊图(Voronoi diagram)(图3),是由一组由连接两邻点线段的垂直平分线组成的连续多边形。从动态角度来看,其形成过程就是以每个离散点为中心,同时等速地扩散涟漪,在涟漪与其他涟漪相撞之前,会形成中心点的“领域面”,面内任意一点距离相应离散点的距离总是最近。

图3 泰森多边形
在计算过程中,若将中心线打散为若干点,求出点的D 值,再以这些离散点为中心创建泰森多边形,将点的值赋予面,即可完成对空间内任意一点的赋值。在实际操作中,D 的赋值效果如图所示(图4),构造点的间隔可以根据研究需求放大或缩小,以此来控制计算的误差。
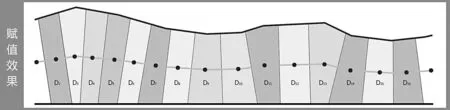
图4 赋值效果预览
2.2 对于H 值
H 值所面临的主要是街道两侧不等高的问题。取单边或取最值的方法显然不够严谨,相对而言求平均或者就近取值的方式比较能够体现计算过程的客观性。研究中可以根据需求选取不同的计算方式,此处仅介绍上述两种比较典型的基本算法:
(1)就近取值:将街道两侧边线同时打散成点,并通过建筑矢量面赋予它们高度值,以这些点为中心创建泰森多边形,完成面内任意一点的赋值。
(2)取平均值:将街道两侧边线分别打散成点,获取高度之后分别创建泰森多边形。通过自定义分辨率将多边形转化为栅格面,以此得到两张H值的栅格图,将两个图层叠加取平均值,通过裁剪即可得到研究区域内任意一点的平均H 值。此处,两次赋值的栅格的分辨率要设置相同,以便于叠加计算。
2.3 后期处理
在数学处理的过程中,创建的泰森多边形一般是不规则且范围较大的,其中超出街道空间范围的点只有数学含义而没有空间意义,因此需要使用研究区域的范围去裁剪D 值和H 值的栅格数据,并将两者相除,得到铺满整个街巷空间的D/H 值栅格图。此时,图内任意一个像素点均被赋予了D/H 值,通过色带拉伸就可以直观反映出街巷内D/H值的变化情况。与此同时,D/H 栅格可以与其他空间要素再度叠加,很大程度上拓展了D/H 值的应用范围。
3 以柯坦老街为例的实践研究
上文详细介绍了D/H 值扩展算法的数学原理。在实际研究中,许多图形处理软件都能够支持类似的分析操作。本文以ArcMap 为例,借助GIS 平台对柯坦老街的宽高比展开研究。
3.1 数据准备阶段
要对D/H 值进行精准计算,前期的测量工作是必不可少的。而根据具体的研究需要,数据质量也有一定的弹性空间——高级别、精细化的专项研究应当进行详细的街道测绘;大范围、批量化的计算只需一张基础地形图即可。
一般认为,在足够大的空间广度下,可以通过建筑性质和层数推算高度,缺失的部分细节对计算精度的影响在可接受的范围。正如精细化的测绘图很难大量获取一样,数据的质和量可以根据研究需要进行合理的平衡。
3.2 前期处理阶段
以地形图的处理为例,首先将测绘数据导入GIS 系统并分层,建/构筑物以多边形要素的形式储存,道路边线以线要素的形式表现。随后,使用“制图工具—制图综合—提取道路中心线”工具,提取街道的中心线,选中该线,使用编辑栏中的“构造点”工具将中心线打散为若干点要素,点的密度可以在参数中进行设置。同理,沿街道两侧边线创建相同密度的离散点。
3.3 要素赋值阶段
使用距离工具,计算中心线上离散点距道路任意一边的距离。将计算结果赋予对应点,再通过字段计算器翻倍,即得到中心线上任意点的D值信息。使用转换工具,将地形图的文字标注转换为点要素,文字符号作为备注属性,分别赋予相应的生成点,每个点要素都记录了该点处的建筑层数。通过空间连接,将点要素所含的层数信息赋予建筑面,再使用字段计算器乘以一定的层高比例,即能得到研究区域内所有建/构筑物的高度信息。
再次,通过空间连接,使用街巷边线生成的离散点抓取建筑物的高度信息,至此,街道边线的H值信息定义完成(图5)。
图5 以点为基础的赋值方法
最后,使用“分析工具—邻域分析—泰森多边形”工具,通过上述已经赋值的点创建泰森多边形,将D 和H 的值由点向面推及。
3.4 计算及可视化处理阶段
使用转换工具将泰森多边形转换为栅格数据,映射D 或H 的属性值,获取两个分辨率相同的栅格图层。最后,将两个栅格层相除,通过裁剪获得研究区域内D/H 值的栅格数据。
最终数据的可视化有多种途径。最常规的是通过图层属性设置,以色带拉伸的方式展现不同数值的分布情况(图6),当然也可以借助WebGL,通过其他可视化平台实现更加生动形象的数据展示效果。
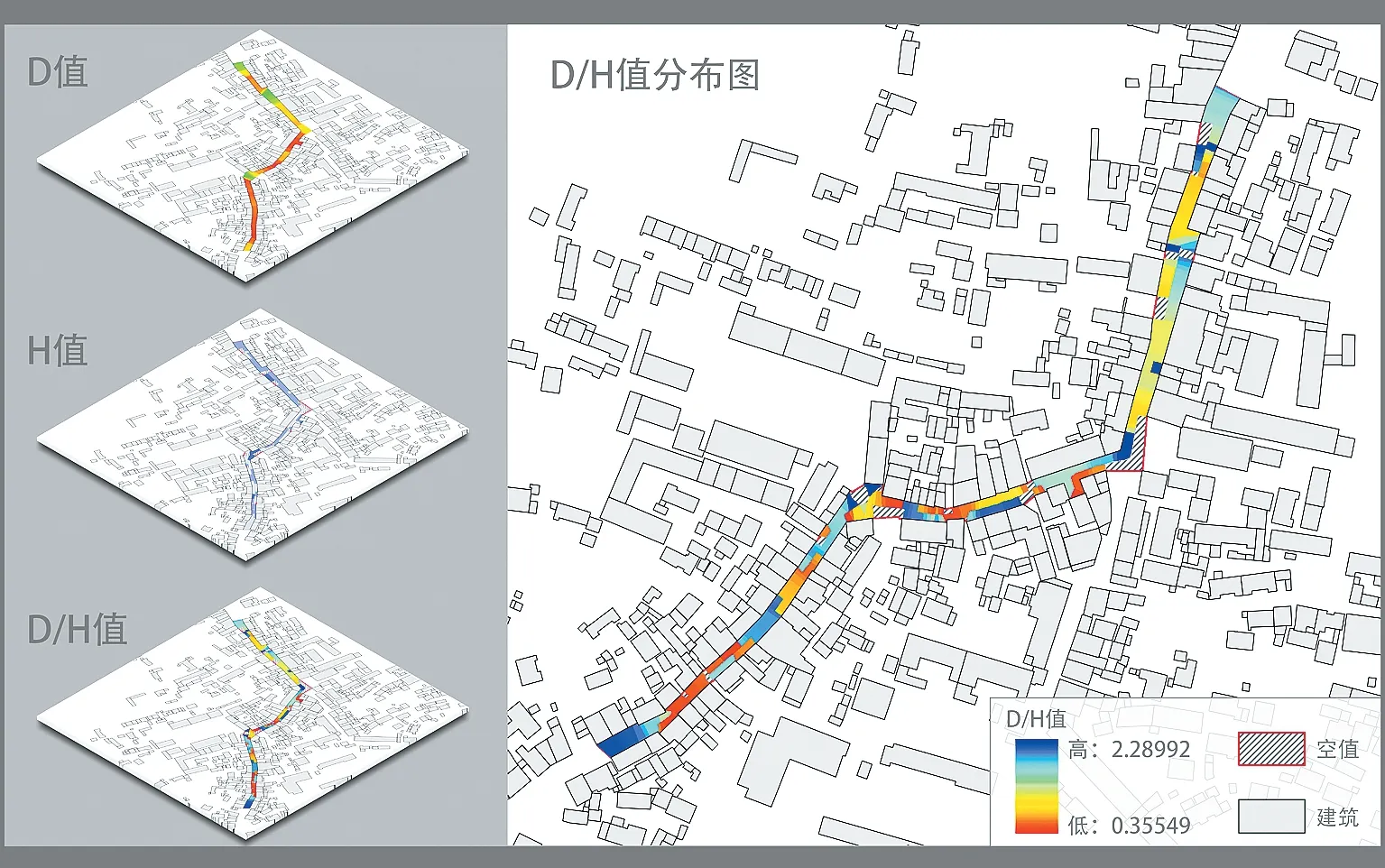
图6 柯坦老街D/H 值分布图
4 基于D/H 栅格数据的应用拓展
栅格数据的应用十分广泛。纵向上,可以对D/H数据进行二次处理,深入挖掘空间的几何属性。例如通过频数统计把握空间的形态特征、通过求导研究空间的节奏变化等等。横向上,D/H 值能与多领域、多层面的要素联合进行回归分析,探究其与空间停留性、相对客流量等其他要素的内在关联。此外,D/H 栅格更可以直接作为参数图层,代入空间评价等计算研究。总而言之,只要理论上有所关联,它几乎可以参与一切空间分析的运算(图7)。
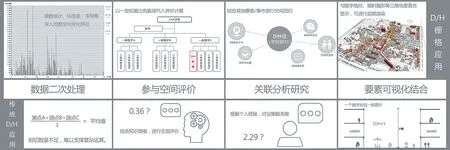
图7 D/H 栅格数据应用示意图
5 应用实例——街道宽高比(D/H)与空间停留性的相关性研究
从柯坦老街D/H 栅格的频数统计结果来看,街巷宽高比在0~2 之间的街道面积仅占总面积的20%,2~2.4 之间的占比则达80%以上,另有约10%的像元值大于3。由此可以看出,柯坦老街的空间形态较一般的皖中传统街巷更为开敞。接下来本文仍以柯坦老街数据为例,基于D/H 栅格对街道宽高比与空间停留性的相关性展开研究。
5.1 空间停留性的量化调查
“空间停留”的相关研究在环境行为学中较为常见。扬·盖尔将停留行为分为3 类:必要性停留、自发性停留和社会性停留[12]。其中必要性停留指购物、候车等行为,受空间环境影响不大;社会性停留包括偶遇攀谈、观看表演等,某种程度上也属于必要性停留。但就实际调研过程来看,研究区域位置偏僻,人员流动性较小,村民攀谈地点的选择带有明显的目的性,且选点重复率很高,不能判定为随机偶遇,因此可以将长时间攀谈也作为群体自发性停留纳入调研范围。
对停留性的量化调研通常是从停留点的空间分布和停留时间两个角度展开。为避免极端因素(如暴晒、街面积水等)对调查对象的自然停留行为产生严重影响,数据的收集时间选定在7 月5 日下午小雨后两小时。为了减弱温差、天光、社会时间等因素对调查结果的干扰,调查的过程控制在一小时以内,也正因如此,调查过程中仅收集到33 组有效数据(图8)。
5.2 D/H 值与停留点分布的空间回归分析
相关性分析通常都是借助数学回归的方法。经典回归分析要求各变量独立、随机,而空间对象是存在自相关的,因此传统的线性回归不太适用于空间分布的研究。空间回归模型在20 世纪70 年代后期开始出现,并逐步成熟,它尝试把数据的属性与空间位置结合起来,从而更好地解释地理事物的数学关系[13]。
本例研究的重心并非探究影响空间停留性的因素,因此无须构建完整的多元回归模型。只需通过全局Moran's I 统计来衡量相邻的停留点D/H 值之间的关系即可。Moran's I 的取值范围为-1~1,正值表示空间分布与属性值分布存在正相关性,负值反之,0 值表示不存在相关,即空间随机分布。
由于D/H 栅格可以提供街面上任意一点的D/H 值,所以只需在GIS 中加载停留点,使之作为测点从栅格面上抓取D/H 值,再使用Spatial Statistics Tool中自带的Moran's I 工具直接展开分析即可(图8)。

图8 停留点信息及全局Moran’s I 分析图
本例研究中Moran's I 指数为0.18,表示停留点的分布与D/H 值分布具备一定程度的正相关,但z值仅有1.25(在95%置信条件下,z 的绝对值大于1.96 才被认为具有显著的空间相关性),意味着观测点针对D/H 值的集聚性非常微弱,同时0.21 的p值(即该数据由随机过程产生的概率达到21%以上)已然超出置信区间,因此上述分析结果基本可以做如下解读:
在柯坦老街的近人尺度下,街道D/H 值变化与自发性停留点的空间分布没有显著的相关性,换言之,D/H 值对停留点的选择不会产生较大的影响。
5.3 D/H 值与停留时间的线性回归分析
影响停留行为的因素通常来说是综合且复杂的,若要探究停留时间的影响因素,应当通过详细的调研结合专家咨询构建完善的多元回归模型[14]。而本例中只探讨D/H 值与停留时间的线性关系,因此仅将D、H、D/H 三种基础数据代入运算。事实上,这样虽然会导致较高的残差和方差膨胀因子,但并不妨碍检验两者线性关系的显著性。
与之前的空间自相关分析一样,ArcGIS 本身也提供了一般线性回归的函数工具。通过停留点抓取D/H 值之后可以直接利用Spatial Statistics Tool下的OLS 工具进行分析。本例的分析结果如下(表1、表2)。
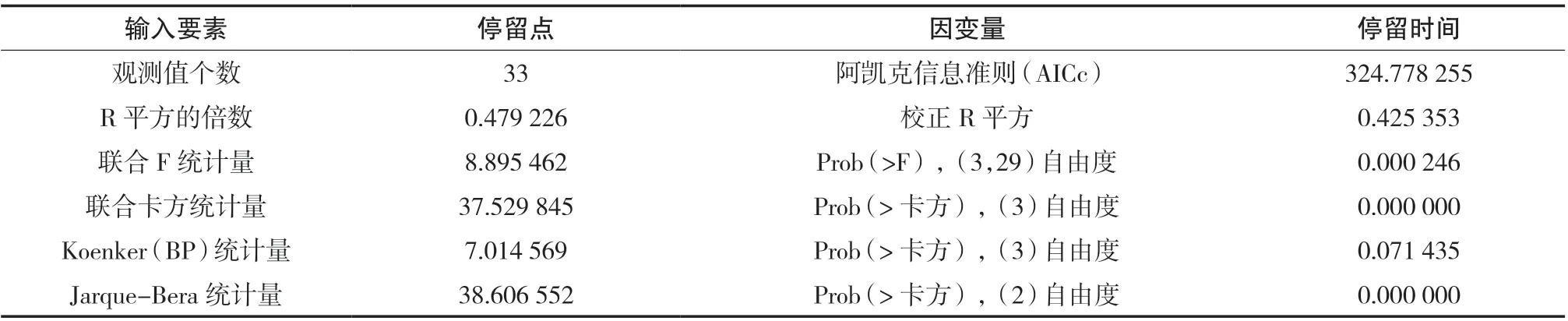
表1 OLS 诊断表

表2 OLS 汇总表
(1)OLS 诊断分析结果解读:
首先,矫正R 平方在0.0~1.0 范围内变化,其值越大代表拟合效果越好,此处该值为0.425 353,拟合效果尚可。
其次,观察Koenker(BP)统计量,其中Prob 大于0.05,不具有统计显著性,也就是说模型具有稳定性。再参考“联合F 统计量”来确定整个模型的统计显著性。此时,Prob 为0.000 246,远小于0.01,因此可以否定零假设,即自变量对因变量有作用。
最后,观察Jarque-Bera 统计量,该值用于指示残差。对于相对完善的模型,残差分布会与典型钟形曲线或高斯分布类似,当Jarque-Bera 统计量小于0.05 时,残差不呈正态分布,指示模型有所偏差。本例研究重在探讨D/H 值与因变量停留时间的线性关系,并未构建完整的多元分析模型,所以此处的残差也在意料之中。
(2)OLS 汇总表分析结果解读:
通过表格中概率的数值可以判断对应系数的可靠性。在D、H、D/H 三类自变量中,只有D/H 值的概率小于0.05,即对于大小为95%的置信度,只有D/H 的系数是可靠的。本例中D/H 的系数高达116,可见D/H 值与停留时间存在明显的正相关。
综上所述,本例研究可得出基本结论:
在柯坦老街的近人尺度下,街道D/H 值变化与自发性停留点的空间分布没有明显的相关性,但与停留时间呈显著的正相关。
6 结语及展望
本文从D/H 值的数学含义出发,对传统算法进行了一定程度的深化研究,新的研究方法对比以往,具备以下几点显著优势:(1)计算过程更加客观,能够真实反映街巷的空间形态;(2)研究精度提高,在实现全域分析的同时,能够以自定义分辨率的方式满足各类研究的弹性需求;(3)成果表达更加直观,街巷空间特征的差异化更加明显;(4)通过创建D/H 值栅格,使宽高比能够作为参数代入其他分析运算,为后续的扩展研究创造更多的可能。
本文以柯坦老街为例,借助GIS 平台进行了实践研究。在创建D/H 栅格的基础上进一步探究街道D/H 值与空间停留性的内在关联,为类似的发散性研究提供了技术参考。
然而,本例研究只是针对街巷水平层面的空间变化进行了算法优化,在纵向上没有详细展开。现实中并非所有的建筑沿街面都是完整的垂面,如遇大量架空或垂直进退关系明显的特殊界面,则需要借助语义差异和数学统计相结合的方法进行空间感受的等效评估,通过计权网络实现街道空间形态的精准量化研究。
——目镜套筒

