蒙特卡洛模拟在核电项目进度管理中的应用

李经春

(中广核工程有限公司，广东 深圳 518000)

0 引言

核电项目投资大、建设周期长，涉及的供应链和参建方众多，建设过程中易受国内外各种因素的影响，不确定性较大，可能会出现建设工期不可控、投资收益不高甚至无法收回投资的情况。项目财务模型分析的一个重要输入条件是项目可能的总工期，在项目建设过程中，总工期的变化会影响资金分布以及项目策略的制定。因此，对项目总工期及其变化趋势的合理评估和研判，对投资人以及其他参建方来说都是至关重要且长期持续的工作。本文旨在提供一种使用概率论的方法对核电项目进度分析和管理的思路。

1 蒙特卡洛模拟概述

1.1 蒙特卡洛方法

蒙特卡洛方法是由冯诺伊曼等科学家在20世纪40年代提出的一种以概率和统计学为基础的、使用随机数解决很多计算问题的方法。将所求解的问题与一定的概率模型建立联系，使用计算机进行大量模拟，获得所求解问题的统计学特征，分析得到实际问题的概率解。

蒙特卡洛模拟可充分考虑项目活动涉及的工期、成本、资源和逻辑关系等方面的不确定性，一次模拟由多次迭代组成，每次迭代都代表一个可能的结果；重复大量模拟后，可得到各项活动的工期概率分布和项目总工期的概率分布。对模拟结果进行进一步分析，可以确定具体活动落在关键路径上的概率，不同总工期情况下的概率以及在期望的置信水平下项目总工期及其最大风险因素。

Crystal Ball是一个嵌于Microsoft Excel的蒙特卡洛模拟工具，提供了多种可供选择的不同的概率分布模型。借助蒙特卡洛模拟工具进行模拟分析的主要步骤如下：

(1)在Excel中建立核电项目进度分析模型。

(2)定义进度分析模型的输入和输出。

(3)设置模拟次数进行模拟运行。

(4)对模拟结果的统计学特征进行分析得到问题的解。

1.2 模拟运行次数估算

影响实际问题的因素多种多样，不可能全部罗列出来，蒙特卡洛模拟是通过研究样本的统计学特征来反映总体样本的特性，每一次模拟相当于一次随机抽样，通过设置合适的样本数量来研究总体特征。假设样本容量达到一定程度时，则有

(1)

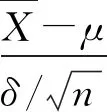
在显著性检验中，右边检验的拒绝域公式见式(2)

(2)

式中，zα为标准正态分布的分位点，其中α表示显著水平。

对式(2)进行变形可以得到样本容量n的计算公式见式(3)

(3)

2 核电项目蒙特卡洛模拟应用实例

核电项目涉及面广、作业活动多，进度逻辑关系较为复杂，常常存在多条不同的主次关键路径，在建设过程中关键路径也经常发生变化。但是，从核电项目进度计划编制的角度分析，一般会将核岛反应堆厂房的建安调试等与主回路相关的活动作为主关键路径进行编制，该关键路径的工期基本决定了项目最短工期，也是对核电项目总工期进行分析和研究的基础。

2.1 某核电项目反应堆厂房关键路径网络图

某核电项目反应堆厂房关键路径网络图如图1所示，分析该核电项目在72个月的工期内完成的概率，对总工期影响较大的活动以及对项目总工期进行优化。

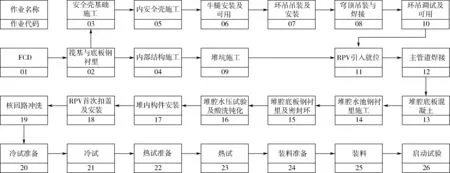
图1 某核电项目反应堆厂房关键路径网络图

各项活动的逻辑关系确定之后就需要确定其可能的工期，采用“专家判断”和“类比估算”等工期估算方法对各项活动的持续时间进行估算，可以得出各项活动在不同条件下的最乐观工期(To)和最悲观工期(Tp)。

2.2 蒙特卡洛模拟过程

在进度计划的活动之间分别存在“完成到开始(FS)”“完成到完成(FF)”“开始到开始(SS)”和“开始到完成(SF)”4种进度逻辑关系。根据每项活动与其紧前或后续活动之间的进度逻辑关系、提前量和滞后量以及估算工期可以计算出项目关键路径的最早完成时间，即项目的总工期。据此建立该项目进度分析模型，见表1。

表1 某核电项目进度分析模型

(续)

首先，根据估算得到的最乐观工期和最悲观工期，使用Crystal ball工具对蒙特卡洛模拟的假设单元格(F列)进行定义，作为蒙特卡洛模拟的数据输入，选择贝塔分布作为其分布函数，并为贝塔分布选择合适的形态参数；然后，把通过进度逻辑关系计算得到的项目可能最早结束的单元格定义为预测单元格(H26)，也就是进行蒙卡特洛模拟的输出数据。至此，就建立了各项活动的参考工期、输入单元格与模拟输出单元格之间的进度联系。每次模拟时，输入单元格都会根据其参考数据和选定的概率分布进行一次随机取值，并通过进度计算得到一个总工期的随机模拟值，重复多次模拟之后就可以得到总工期的概率分布和统计学特征，对其进一步分析可以得到实际问题的概率解。

因此，设置本次模拟的次数为60 000次，大于估算的样本容量，满足假设要求；在Crystal Ball中进行设置并模拟运行，得到模拟结果如图2所示。

图2 某核电项目总工期预测概率分布图

从图2可以看出，在本次模拟中该项目在72个月内完成的概率仅为2.23%，几乎不可能按期完工，项目可能的总工期范围宽，不确定性较大。

模拟得到的主要统计特征见表2。

表2 某核电项目工期的主要统计特征

2.3 敏感性分析

敏感性分析是从定量分析的角度研究有关因素发生变化对某一个或某一组关键指标影响程度的不确定性分析方法。通过敏感性分析可以识别输入变量对系统输出结果的影响程度，从而识别关键影响因素。在进度计划中，项目工期的不确定性是由各项活动的不确定性及其相互之间的进度逻辑关系综合作用的结果，对项目工期进行敏感性分析可以识别出各项活动的不确定性对总工期的不确定性的影响程度。通过Crystal Ball对该核电项目的敏感性进行分析，结果如图3所示。

图3 某核电项目工期的敏感性分析结果

从敏感性分析结果中可以看出，对项目总工期不确定性贡献较大的几项活动为：内部结构施工、装料准备、热试准备、启动试验、环吊调试及可用等。因此，需要提前关注这些活动，做好风险预案，项目实施过程中重点关注相关活动的进度控制、风险控制，以降低项目总工期的不确定性风险。

2.4 趋势分析

通过敏感性分析识别出对项目总工期不确定性影响较大的活动后，针对这些活动制订优化方案、风险预案，采取加强进度控制等措施，可以实现减小相关活动工期、降低作业风险的效果，但同时也会伴随资源投入的增加，需要综合考虑相关投入和收益，进行具体量化的分析之后才能决定最终方案。对不同的方案进行趋势分析，可以对比在不同方案、不同可能性的条件下项目总工期变化的量化指标，有助于选择最合适的项目方案。

通过对项目总工期不确定性敏感度较高的活动制定优化措施，改变其模拟输入条件，可以得到不同的优化方案，各优化方案下项目总工期的概率分布对比情况以及不同概率下总工期的变化趋势如图4和图5所示。

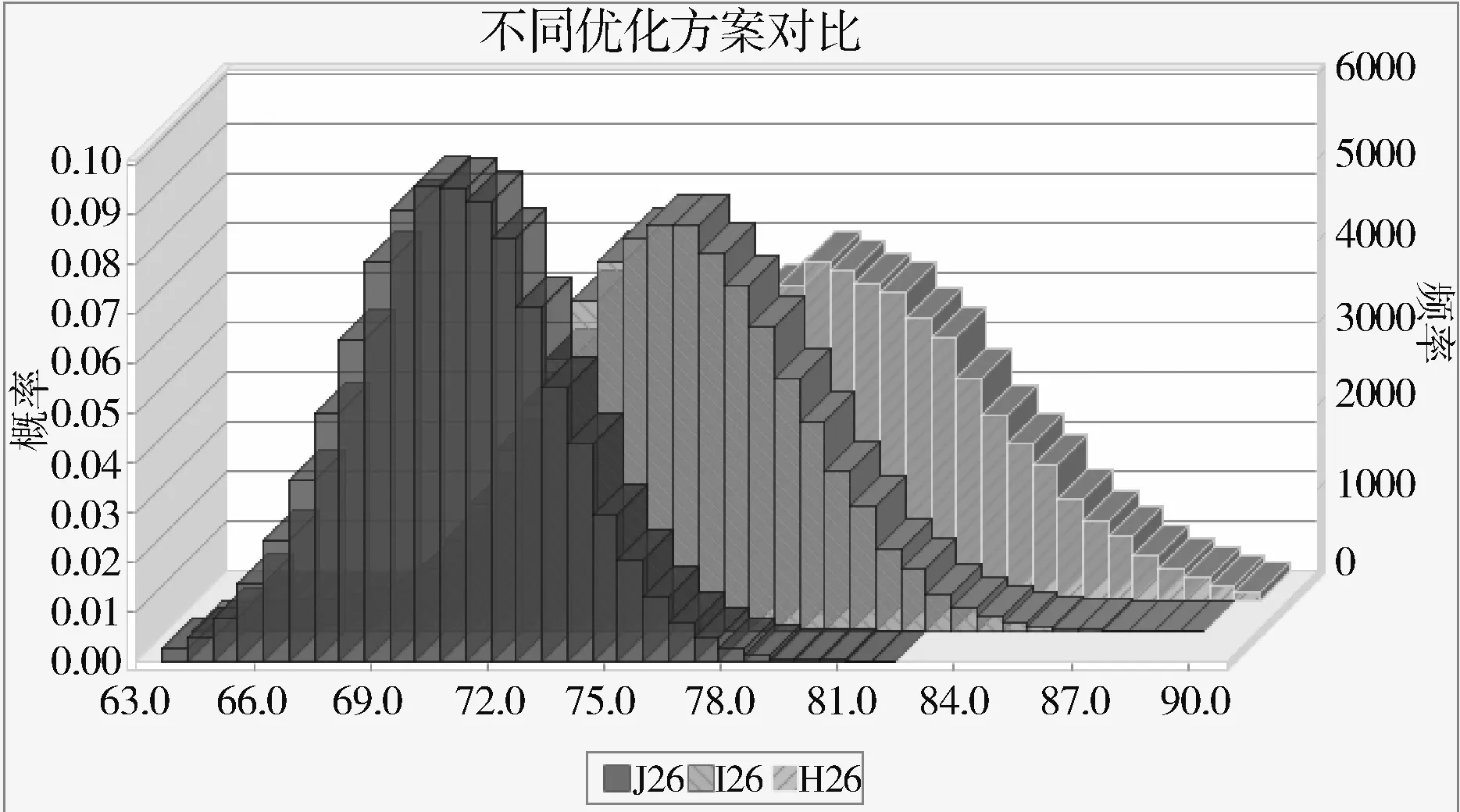
图4 不同优化方案对总工期的影响对比

图5 不同方案项目总工期变化趋势

通过优化，项目在72个月内完成的概率从原方案(H26)的2.23%变成方案一(I26)的11.0%和方案二(J26)的65.3%，配合各方案资源投入的情况选择合适的总工期方案。另外，项目总工期的其他统计学特征也发生了相应变化，对比情况见表3。

表3 不同方案下项目总工期的统计特征对比

3 结语

对于核电项目这种总持续时间长、各项活动工期不确定性较大的复杂项目，运用蒙特卡洛模拟可以直观地将项目工期的不确定性用概率的形式表现出来，为项目财务分析和项目决策提供量化输入。蒙特卡洛模拟时每项活动的概率分布不局限于贝塔分布，而可以根据情况选择一些常见的其他分布，如三角分布、PERT-贝塔分布、一致分布等，既可以是连续分布，也可以是离散分布，可以大幅提高模拟的灵活性和适应性；通过敏感性分析和趋势分析可以定位关键活动，对比不同方案对总工期的影响的量化结果，帮助项目决策者制定更加合理的决策。