潜标锚泊系统静姿态与涡激振动时频分析
陈廷威,张学刚,吕 帅,宋宪仓
(1.中国海洋大学工程学院,山东 青岛 266100;2.中国船舶重工集团有限公司第七六〇研究所,辽宁 大连 116001)
单点系泊潜标系统是一种较为普遍的海洋信息获取装备,通过在潜标系统上面悬挂各种功能设备测量不同的海洋环境指标,目前已被各国广泛应用。一般在潜标系统布放之前,需要根据具体用途及相关海域的实际情况,对系统整体的设备布置、浮力配置和连接方式进行设计,对系统的静姿态和动力特性进行分析。由于海流、波浪等复杂流体的作用,系缆周围会产生漩涡,进而在垂直于轴向和来流的方向产生周期性交变力,引发锚泊系统的涡激振动。严重时会干扰信号,限制测量仪器的稳定性和灵敏性[1],所以有必要对潜标锚泊系统的涡激振动特性进行深入研究。
已有一些学者对潜标系统的静力特性进行了研究。齐占峰等[2]通过编制程序,模拟在不同海流条件下潜标系统的姿态和受力问题;马龙等[3]进行了深海潜标系统的姿态模拟计算和优化配置分析;王蓓等[4]对一套潜标进行了建模分析,对潜标异常沉降问题进行了探究。潜标系统静力分析的理论本身并不复杂,但是静力分析的结果与实际海试结果仍具有一定的出入,静力分析的准确性有待提高。针对潜标锚泊系统涡激振动的研究实际上是研究细长圆柱体的涡激振动响应,而且相较于研究较多的潜标静力分析,时域涡激振动的研究相对较少。常用的涡激振动研究方法可分为三类:一是实验法,包括实海实验与模型实验;二是数值模拟法,YAMAMOTO C T等[5]用数值模拟的方法研究了柔性圆柱涡激振动;三是理论推导经验模型法,在理论基础之上加上实验数据结果进行修正,本文采用此类方法。
本文研究目标是通过对锚泊系统静姿态的计算和涡激振动振幅与频率的分析,为潜标系统在浮力配置、设备安排等方面提供依据。
1 基础理论
1.1 静力分析
要实现潜标锚泊系统的模拟计算分析,需要将连续的结构体离散成有限个单元,采用独立的质量点来描述每个单元的质量,利用无质量的弹簧来描述每个单元的刚度[6]。由于潜标的主体位于水面以下,在静力分析过程中,除了自身的重力和浮力外,仅需要考虑海流的影响,取锚泊系统第i个单元进行受力分析,如图1所示。
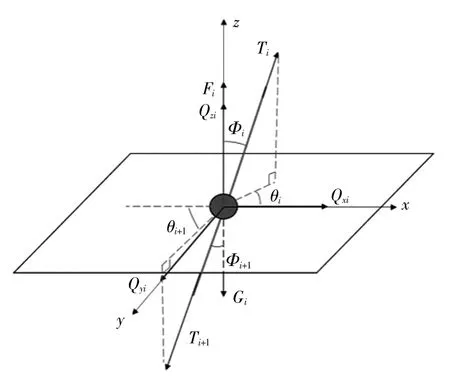
图1 静力分析图
作用在第i个单元上的荷载包括重力Gi、浮力Fi,3个方向上的拖曳力Qxi、Qyi、Qzi和两端系缆的拉力Ti、Ti+1。单元上半段与z方向的夹角为φi,在x-y平面上的投影与x轴的夹角为θi,单元下半段与z方向的夹角为φi+1,在x-y平面上的投影与x轴的夹角为θi+1。由此可得3个方向的受力平衡方程,见式(1)、式(2)和式(3)。
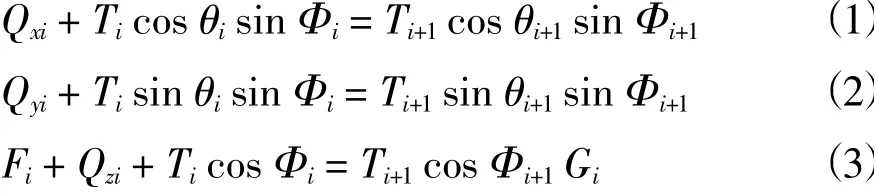
在海流拖曳力的作用下,经过多次迭代计算,潜标系统由初始状态慢慢趋向于平衡状态,并可据此推算单元的位置和偏角信息,其中作用在系缆上的拖曳力可以通过式(4)计算。

式中,ρ为海水密度;j=j(x,y,z);CDj为j方向上的拖曳力系数;Aj为j方向上的拖曳面积;vj为j方向上的流体相对于设备的速度,v是流体总流速。
1.2 时域VIV模型
当水流流经潜标系缆时,由于流体的粘性效应,边界层将会发生分离从而产生涡泄,进而在系缆周围产生周期性的压力变化,这种变压力产生的涡激力将会引起潜标系缆的涡激振动。根据涡激振动的机理提出理论经验模型模拟并对模拟结果进行分析论证是研究涡激振动的主流方法。OrcaFlex软件嵌入了5种理论经验模型,如图2所示。
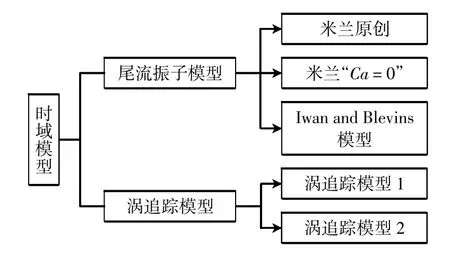
图2 时域模型分类图
尾流振子模型[7]是一种单自由度预测模型,只模拟横向的VIV运动,是尾流运动方程和圆柱运动方程的耦合。基于这一理论的米兰模型[8]由意大利团队开发,米兰原创模型与米兰“Ca=0”模型的区别在于Ca的取值,前者Ca=1.0,后者Ca=0。Iwan and Blevins模型是由Iwan和Blevins从动量理论的角度发展而来的,并根据固定和受迫圆柱的实验结果对模型进行了校准,然后将模型的预测与相应的实验结果进行了比较。
涡追踪模型比尾流振子模型计算量大得多。它们基于边界层理论的基本物理方程和Navier-Stokes方程,是一种模拟了全流场的计算流体动力学模型,这种方法重点在于追踪涡量,而且涡量常常局限于狭窄的片状区域,从计算的角度来看,这样做效率要高得多。涡追踪模型1是对最初的涡追踪模型的实现和发展,它使用可变时间步长,涡追踪模型2是对涡追踪模型1的简化,使用定时间步长,两种模型分别侧重于计算精度和计算效率。
2 潜标系统静态验证
本文使用兰志刚等[9]在文中提到的潜标系统进行建模计算,与其计算结果进行对比验证,证明潜标系统和环境参数设置的正确性,同时也为后续系缆涡激振动计算提供静态信息。根据该文献,对于拖曳力系数,直径较大的球体取为0.65,直径较小的球体取为1.0,圆柱体取为1.0~1.3。
2.1 潜标系统介绍
潜标布放海域水深1 200 m,潜标长度700 m,具体布置如图3所示。
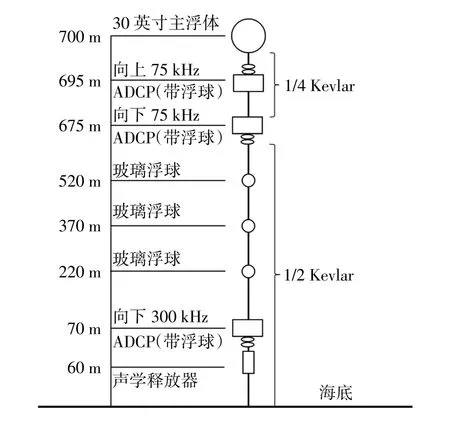
图3 700 m潜标系统布置图
潜标系统主要设备具体参数见表1和表2,表中拖曳面积对应的方向顺序为x、y、z。海流剖面流速可以通过公式(5)计算得到。

表1 主要设备相关参数

表2 Kevlar相关参数

合流速计算见公式(6)。

式中,Ux为x方向流速;Uy为y方向流速;U为合流速;z为距底面高度。
2.2 结果对比分析
根据以上潜标系统配置,在OrcaFlex中建模计算获得潜标系统的姿态、张力和偏角数据,如图4所示。图4(a)、图4(b)和图4(c)分别为计算平面姿态、系缆拉力和系缆沿水平偏角与原文献结果的对比。
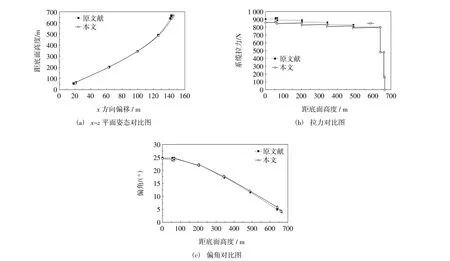
图4 本文和原文献的姿态、拉力和偏角对比
根据数据统计,本文与原文献x-z平面相同位置最大高度偏移为3.4 m(0.48%),最大上端张力差为171.5 N,最大下端张力差为130.3 N,最大上端偏角差为0.4°,最大下端偏角差为0.4°。根据以上x-z平面姿态、拉力和偏角的对比,两者吻合情况较好,表明潜标系统和环境参数的设置与原文献基本一致,可以作为后续涡激振动计算的基础模型。
3 时域模型优选
本文基于CHAPLIN J R等[10]在Delft实验室进行的立管模型实验,对该模型实验独立建模计算,并且与模型实验结果和OrcaFlex官方验证结果[11]分别做了对比验证并优选出后续所用的时域模型。
3.1 Delft模型实验介绍
实验水池深6.5 m,水池中有一个大型钢结构制造的运动部件,部件底部为立管提供一个刚性的安装点,上端固定有一个7.54 m高的真空罐,通过从上端抽取空气形成负压,当真空罐开口处于水下时,大气将水压入真空罐上部,将长为13.12 m的立管安装在底部的刚性安装点和真空罐顶部的连接处,底端距离水底0.36 m,图5为Delft实验示意图。当运动部件按照设定工况运动时,下端由于相对运动造成一个均匀流,上端由于立管与真空罐内的水保持相对静止,所以上端立管在运动过程中处于静水状态。
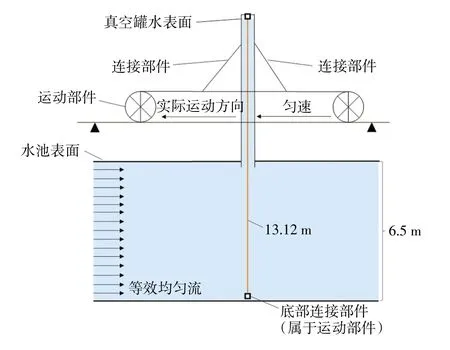
图5 Delft实验示意图
3.2 阶跃流作用下的响应
模型在阶跃流的作用下与立管发生动力响应,阶跃流的计算方法见公式(7)。
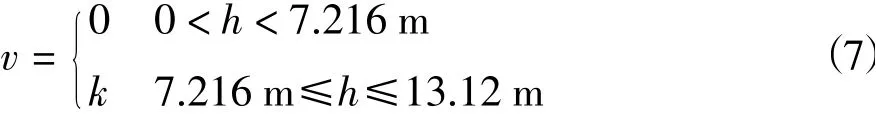
式中,h为立管从顶端到下部各点的长度;k为拖曳速度,其值与实验工况有关,表3给出了9种实验工况下的拖曳速度和顶张力数据。对5种时域模型分别计算以上9种工况,进而可以将计算结果与已有结果进行对比。

表3 9种工况下的拖曳速度和顶张力
3.3 相关分析
针对5种模型的系缆振动最大位移计算结果,在每条包络线上取出83个点作为每种模型工况的特征点进行相关计算分析,相关分析指标选择RSquare。R-Square为决定系数,可以表征一种变量被另一种变量解释的程度。每种模型的9种工况对应一个相关分析数值,对其取平均得到该模型的相关分析结果,表4是5种模型的相关分析结果对比。

表4 本文、实验和软件官方相关分析结果对比
根据相关分析结果可知,本文计算结果与OrcaFlex官方提供的结果吻合度较高,具有较高的可信度;本文计算结果与Delft模型实验测量结果应用米兰原创模型计算相关性最高,故选用米兰原创模型作为后续VIV时域分析的经验模型。
4 700 m潜标涡激振动计算与分析
根据上节优选方案,选择米兰原创时域模型作为700 m潜标涡激振动时域计算模型。在保证示例其他条件不变的情况下,选取表面流速分别为0.25 m/s、0.5 m/s、0.75 m/s、1.0 m/s、1.25 m/s、1.5 m/s、1.75 m/s、2.0 m/s,计算不同流速下的涡激振动响应,流速剖面如图6所示。

图6 8种工况流剖面图
每种工况的计算时长为300 s,根据计算结果,8种工况下节点涡激振动最大主周期不到1 s,选取100~300 s作为时域分析时间段,可以充分保证分析时间段为稳定的涡激振动段。
4.1 节点时域图
为直观表征8种工况下VIV的时域振动特性,选取系缆主浮体位置和第2个玻璃浮球位置的100~300 s的时域位移图进行分析,如图7和图8所示,图7(a)和图7(b)是主浮体处前4种工况和后4种工况时域图,图8(a)和图8(b)是370 m处浮球前4种工况和后4种工况时域图。
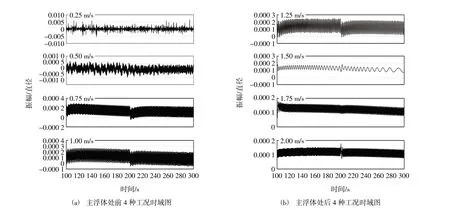
图7 主浮体时域图
一般节点的位移振动原点在姿态原点位置,从图7(a)和图7(b)中可以看出主浮体在0.25 m/s和0.5 m/s工况下时,位移振动原点还在姿态原点;而后6种工况下,主浮体的振动原点位置发生了偏移,且在200 s时发生突变。图8(a)和图8(b)可以代表系缆上绝大多数节点的振动状态,从位移振幅看,随着流速不断增大,整体上呈现下降趋势,后几种工况下位移振幅趋于振荡;从位移形态看,随着流速的增大,振动越来越紊乱,周期性越来越不明显,但都是围绕姿态原点的振动。

图8 370 m处浮球时域图
4.2 幅值分析
从时域位移图中取振幅最大值,每隔1 m取一个节点,8种流速工况每两个工况成一个图,如图9至图12所示。图9至图12分别为0.25~0.5 m/s、0.75~1.0 m/s、1.25~1.5 m/s和1.75~2.0 m/s工况下沿系缆最大振幅对比图。
从图9中可以看出,低流速下沿系缆的最大振幅整体波动较大,呈现一定的周期性特征,而对于流速较高的工况,除一些特别点(如220 m处)外,沿系缆的最大振幅基本维持在高位,如图10、图11和图12所示。从图中也可以看出,随着流速的增大,涡激振动激发的系缆振动模态逐渐增多。

图9 0.25~0.5 m/s系缆最大振幅对比图

图10 0.75~1.0 m/s系缆最大振幅对比图

图11 1.25~1.5 m/s系缆最大振幅对比图
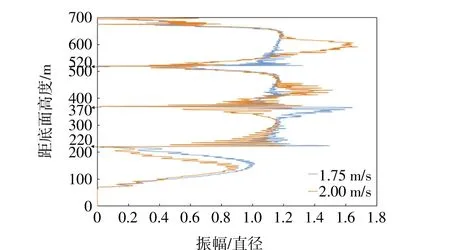
图12 1.75~2.0 m/s最大振幅对比图
不同流速工况下的计算结果也具有一些相似的幅值变化规律,在3个浮球(220、370、520 m处)和75 kHz ADCP(675 m处)布置位置处幅值有明显的降低,说明系缆设备对于系缆本身的涡激振动幅值有抑制作用;对于该潜标系统,每种工况的振幅/直径的最大值和最小值相差不大,最小值在0附近,最大值在1.6~1.8;系缆底部由于锚定的作用幅值逐渐衰减到0。
4.3 频率分析
对于频率分析,时间步长的选择对于计算结果的准确性有很大的影响。过大的时间步长捕捉不到较大的频率,过小的时间步长则会造成计算资源的浪费。图13是1.75 m/s和2.0 m/s两种工况下分别在时间步长0.01 s、0.005 s和0.001 s下沿系缆主频率的对比图。由图13可知,0.01 s的时间步长已经足够满足对潜标系统涡激振动频率的捕捉,故最终选择的时间步长为0.01 s。
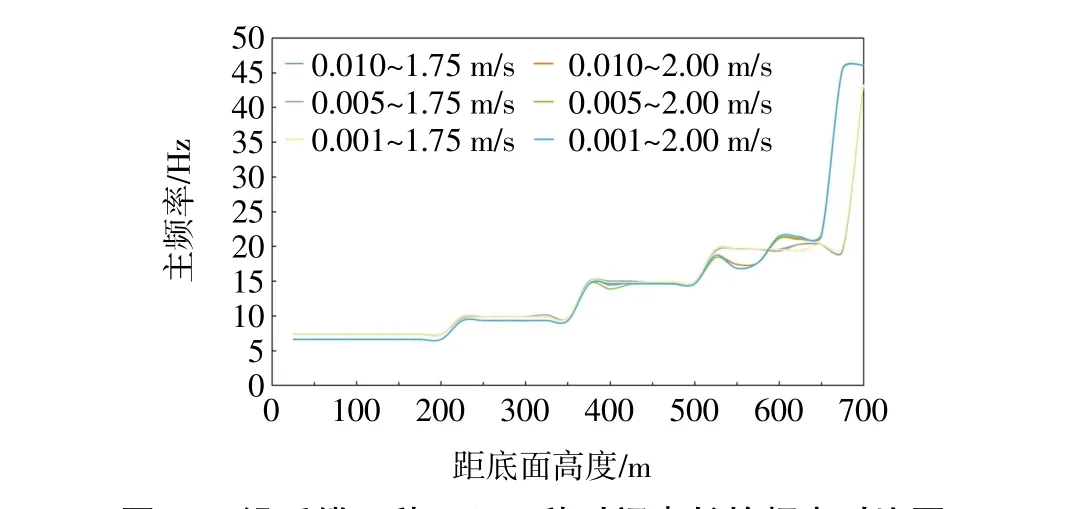
图13 沿系缆2种工况3种时间步长的频率对比图
以时域位移数据为基础,对每种工况进行频率计算并处理,取其主频。每隔25 m取一个点,图14是8种工况下沿系缆25~700 m主频率的对比图。
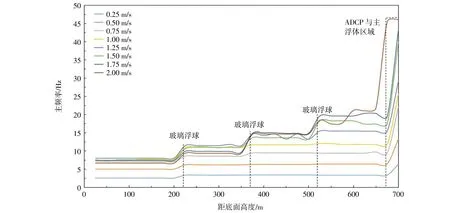
图14 8种工况下沿系缆主频率对比图
从图14中可以看出,当系缆高度保持不变时,随着流速越来越大,主频率越来越大,但是增大的幅度总体上在减小。对于同一流速工况,随着距底面高度的增大,主频率也呈现逐渐增大的趋势。在距底面高度25~675 m之间,3个玻璃浮球将系缆主要分成4段,每一段的系缆节点主频基本保持不变;在玻璃浮球处,系缆振动频率会发生跃变,下一段以一种新的频率振动。在675~700 m之间,存在2个ADCP和1个主浮体,主频率发生较大的跃变。结合图4(b)中的拉力变化规律,可以发现频率变化是由对应的拉力突变导致的。
系缆涡激振动频率一般在50 Hz以下,随着流速的增加,振动的稳定性变差,但仍然保持上述规律。因此,对于系缆设备的这种调频功能,可以通过对潜标系统设备和位置的调整,从而控制系缆上的主频率变化;根据系缆VIV频率振动的特性,可以为水听器等探测设备在分辨率的选取提供依据,为探测结果提供分析素材。
5 结论
本文基于集中质量原理,使用OrcaFlex软件对兰志刚等[9]的一套深水潜标系统进行了静力验证,其静态姿态、系缆张力与偏角均吻合良好,表明潜标系统和环境参数的设置与原文献基本一致,可以作为后续涡激振动计算的基础模型。
根据优选出的米兰原创时域模型计算了8种流速工况下系缆的静态和涡激振动响应,展示了两个特殊点的时域位移图,并对系缆时域位移从幅值和频率两个方面进行了分析。随着流速的增大,主浮体的沉降越来越大,潜标整体的偏移量也越来越大。低流速下的涡激振动最大振幅波动较大,较高流速下的最大振幅基本维持在高位;在有设备存在的地方,振幅会显著减小,8种工况下的振幅/直径范围都在0~1.8之间,并无太大的区别。对频率而言,当系缆高度保持不变时,主频率随着流速的增大而增大,但是增大的幅度总体上在减小。对于同一流速工况,随着距底面高度的增大,主频率也呈现逐渐增大的趋势。在浮球或设备处,系缆主频由于拉力突变而发生跃变;涡激振动频率大小一般在50 Hz以下。
对于该潜标系统,设备的位置设置至关重要。在设备周围,系缆VIV振动最大振幅会变得很小,所以对于系缆振动振幅有要求的水深可以通过设置设备来减小振动。在设备处,系缆拉力会发生突变,通过调整设备的位置可以改善整条系缆的拉力状况,也可以控制整条系缆VIV频率跃变的位置,调整系缆的振动频率分布。根据涡激振动不同工况的频率规律,可以与其他非同频噪声区别开,在探测海洋噪声时可以作为水听器等设备的选择依据。

