缔合勒让德函数的标准向前按列递推公式

2022-01-27 10:56张捍卫李鹏杰

大地测量与地球动力学 2022年2期

张捍卫张华李鹏杰

1 河南理工大学测绘与国土信息工程学院，河南省焦作市世纪大道2001号，454000

研究地球重力场需要计算fnALFs数值及其各阶导数和定积分数值，使用的递推公式目前主要有标准向前按列或行递推公式[1-2]、贝尔科夫递推公式[3]及跨阶次递推公式[4]等。随着卫星重力学研究的发展，需要计算超高阶的fnALFs数值，目前主要通过选择合适的计算方法和修正语言编程2种途径来提高计算速度和扩展递推阶次，如傅里叶级数展开法[5-7]和多项式逼近法[8]等。

标准向前按列递推公式的应用很广泛[9-12]，但这些研究都是通过对算法进行改进来扩展递推阶次。本文不讨论算法，只是在Paul[1]理论研究的基础上完善扇谐项和准扇谐项推导的严谨性，基于fnALFs的2个导数公式给出推导fnALFs定积分递推公式的新方法，且本文给出的递推公式可从第2阶开始递推。

1 关于fnALFs及其积分的按列递推公式

首先给出完善后的fnALFs标准按列递推公式：

(1)

式中，θ∈[0,π]。其中，

fnALFs定积分的标准按列递推公式为：

(2)

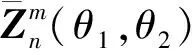
当积分区间很小时，可采用式(3)：

(3)

以上公式的精度评定见文献[1]。

2 关于式(1)的证明

关于n阶的勒让德函数[13-15]为：

(4)

式中，int[·]表示取整数，n=0,1,2,…。

关于n阶m次的ALFs[13-15]为：

(5)

显然，当m=0时，式(5)等同于式(4)。关于fnALFs的定义[13-15]为：

(6)

(7)

根据式(5)可得：

(8)

根据式(8)可直接得到：

(9)

将式(9)规格化，就可得到式(1)中第2种和第3种情况。

3 关于式(2)的证明

定义ALFs的3个定积分公式：

(10)

(11)

ALFs的一个导数公式[15]为：

(12)

另一个导数公式[15]为：

(13)

式(13)可根据式(5)直接得到。设有：

(14)

对式(14)采用分部积分法，并考虑式(10)和式(11)可得：

(15)

同理，根据式(12)和式(13)可得：

(16)

(17)

根据式(7)可得：

(18)

根据式(15)～式(18)可得：

(19)

式(19)只适用于0≤m≤(n-2)的情况。

(20)

在式(19)中，令m=n-1且不考虑等号右端第1项，就等价于式(20)。将式(19)和式(20)规格化，就可得到式(2)中第1种和第2种情况。

(21)

在两极附近y=sinθ值很小，依据式(21)的递推会产生较大误差。根据

可得：

(22)

将式(21)和式(22)规格化，可得式(2)中第3种情况和式(3)。关于式(2)中第3种情况，文献[1]给出的系数为：

(23)

这显然与本文结果不一致。由此可见，文献[1]中的公式只能从第3阶开始递推，而不能从第2阶开始递推。

4 数值计算与分析

第n阶fnALFs数值计算结果的精度检验公式[1]为：

(24)

关于fnALFs数值积分最简单的精度检验公式[1]为：

(25)

图1 公式(1)的适用性(T(n)<10-12)Fig.1 Applicabilty to equation (1)

图1表明，在±23°纬度范围内，式(1)可将fnALFs递推至9 000阶；在±44°、±62°和±86°纬度范围内，可分别将fnALFs递推至3 000阶、2 000阶和1 000阶。在两极区域(纬度绝对值大于86°范围内)，递推公式效果较差。

图2 θ1=45°、θ2=46°且n=2 000阶时积分数值结果Fig.2 Integral numerical results when θ1=45°,θ2=46°,n=2 000

图3 θ1=5°、θ2=6°且n=1 000阶时积分数值结果Fig.3 Integral numerical results when θ1=5°,θ2=6°,n=1 000

5 结语

实际上，ALFs的带谐项(次为零)、扇谐项(次等于阶)、准带谐项(次等于1)及准扇谐项(次为阶减1)很特殊，统称为边界项，在其他形式递推公式的推导过程中表现尤为明显，甚至要扩展边界项范围，边界项的递推必须单独讨论。

ALFs导数公式的应用广泛，由其推导ALFs定积分公式的过程显得很简单。递推公式应明确指出最低可从第几阶开始，不然在应用中难免会出错。根据式(15)～式(18)还可得到如下2个形式的积分公式：

(26)

(27)

式(26)和式(27)只是一个计算式，当然也可得到其递推公式。