“UIR三角模型”构建及应用*
——以高考电学实验题为例
鹿传旺 胡 文 吴兴舟
(山东省淄博第一中学 山东 淄博 255200)
电学实验题是每年高考的必考内容,题目设计灵活多变,创新性强,对学生的科学思维能力要求很高.新的物理课程标准(2017年版)中提出:发展学生的科学思维能力是重要的教学目标之一,构建模型是一种重要的科学思维方式[1].笔者在多年的备考教学中发现,合理巧妙地运用物理模型能够帮助学生提高分析、推理和预测电学实验的能力,有利于降低师生高考电学实验的备考难度.本文将以电学“UIR三角模型”为例,介绍其构建及运用的过程,并辅之以具体的案例来介绍其用途.
1 “UIR三角模型”构建
高中电学实验主要围绕电压、电流、电阻的测量来展开.为了测试学生的科学推理能力,电学实验题目在设计过程中通常会缺失部分实验器材,例如缺失电压表或电流表;在考查学生科学论证、质疑创新能力时,题目设计中会给出充足的器材,学生需要进行甄别,根据实验方案合理选择实验器材,例如给出的电压表、电流表、电阻箱的量程不合适.应对上述情况,学生需要借助欧姆定律进行思维转换去分析.
1.1 缺失电压表或电压表不合适
测电压用“IR-U”思维方式:一个合适的电流表搭配一个已知阻值的电阻就可表达出电压,即将电压U的测量转化为用电流表测量已知电阻值R中的电流I;如果电流表本身的电阻已知,电流表本身也可作为电压表用,读出电流值I乘以其电阻值R便相当于测出了电压U.如图1(a)所示,构建图1(b)所示三角关系模型来表征这种思维方式.

图1 IR-U思维方式
1.2 缺失电流表或电流表不合适
测电流用“UR-I”思维方式:一个合适的电压表搭配一个已知阻值的电阻就可表达出电流,将电流I的测量转化为用电压表测量已知电阻阻值R两端的电压U;如果电压表本身的电阻已知,电压表本身也可作为电流表用,读出电压值U除以其电阻值R便相当于测出了电流I.如图2(a)所示,构建图2(b)所示三角关系模型来表征这种思维方式.

图2 UR-I思维方式
《中国高考评价体系》在回答“考什么”的问题上提出“核心价值、学科素养、关键能力、必备知识”,在回答“怎么考”的问题上提出试题应体现“基础性、综合性、应用性、创新性”的考查要求[2].前面两种情况在“考什么”的问题上侧重物理核心素养“科学思维”的考查,在“怎么考”的问题上更多体现“创新性”的考查要求.用电压表测电压、电流表测电流在电学实验考查中兼具“学科素养,关键能力、必备知识”三重特性,试题适合体现“基础性、综合性、应用性”的考查要求,例如伏安法测电阻.
1.3 不缺失电压表和电流表
伏安法测电阻是高中电学实验最基本、最常用的测电阻的方法,属于“UI-R”思维方式:用合适量程的电压表和电流表分别测出电压U和电流I,借助欧姆定律得出电阻值R.选用如图3(a)所示的电流表内接或外接电路进行测量,但会存在原理误差.若设计成如图3(b)所示电路可消除因电路结构带来的原理误差:先把单刀双掷开关打到1,测出电压U1和电流I1,得出电阻箱、电流表、待测电阻的总阻值R1,再将开关打到2,测出电压U2和电流I2,得出电阻箱、电流表的总阻值R2,进而求出Rx=R1-R2,构建图3(c)所示三角关系模型来表征这种思维方式.

图3 UI-R思维方式
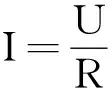
“UIR三角模型”可解读为:基于欧姆定律的关于电压、电流、电阻之间相互关联的具有思维导向功能的三角状模型图,“UIR”的U,I,R分别表示电压、电流、电阻,有时可引申为电压表、电流表、测电阻的仪器.

图4 UIR三角模型
2 “UIR三角模型”蕴含的丰富思维方式
“UIR三角模型”基本的思维导向是电压、电流、电阻中任一个可由另外两个借助合适电路结构来测出.除此之外,若以“IRI”“IRR”“URU”等为顶点构建三角形来表达解决电学实验的思维方式,其内涵会更丰富,分析电学实验问题的思路会更广,现举例如下.
2.1 “IR-I”思维方式
对电流表进行量程改装,就属于这种思维方式.如图5(a)所示,IR-I在“UIR三角模型”中位置如图5(b)实线构建三角形.

图5 IR-I思维方式
2.2 “IR-R”思维方式
正如替代法、半偏法、电桥法测电阻那样,属于用电流、电阻推理分析测量电阻这种思维方式.如图6(a)所示,IR-R在“UIR三角模型”中位置如图6(b)实线构建三角形.
2.3 “UR-U”思维方式
这种思维方式是用电压、电阻推理分析电压,例如对电压表进行量程改装.如图7(a)所示,UR-U在“UIR三角模型”中位置如图7(b)实线构建三角形.

图7 UR-U思维方式
2.4 “UR-R”思维方式
半偏法测电压表内阻等实验属于这类思维方式.如图8(a)所示,其在“UIR三角模型”中位置如图8(b)实线构建三角形.
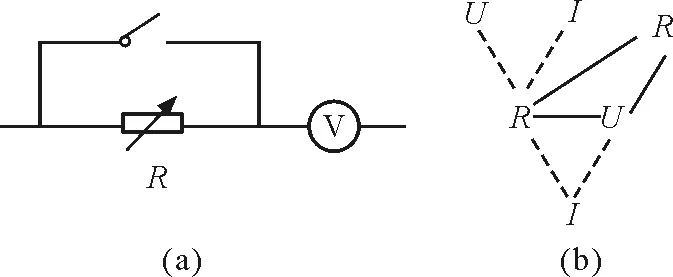
图8 UR-R思维方式
2.5 “UI-U”思维方式
在测电源的电动势和内电阻实验中,可看作依据闭合电路的欧姆定律,借助外电路的电压和电流的测量分析推理电动势.如图9(a)所示,其在“UIR三角模型”中位置如图9(b)实线构建三角形.
2.6 “UI-I”思维方式
在霍尔效应相关实验中,用霍尔元件上的霍尔电压U和通电电流IH分析推理所加磁场对应的电流I,或者用霍尔电压U和所加磁场对应的电流I分析推理通电电流I.如图10(a)所示(图片来自2014年江苏高考物理试题),其在“UIR三角模型”中位置如图10(b)实线构建三角形.

图9 UI-U思维方式

图10 UI-I思维方式
以上是“UIR三角模型”中蕴含的三量间的思维方式.从另外角度看,三角模型中还蕴含两不同量思维方式,比如:“UR”“UI”“IR”,电学实验中的电压表与电阻组合、电压表与电流表组合、电流表与电阻组合进行实验属于此类思维方式.三角模型中也蕴含两同类量间的思维方式,比如:“UU”“II”“RR”思维,例如电学实验中的电压表与电压表组合、电流表与电流表组合、电阻与电阻组合进行实验,在此不再画图举例.
3 “UIR三角模型”运用
下面以高考题为例说明“UIR三角模型”的使用,题目中的设问有节选.
【例1】(2021年高考广东卷物理第12题)某小组研究热敏电阻阻值随温度的变化规律,根据实验需要已选用了规格和量程合适的器材.按图11连接好电路进行测量.

图11 例1题图
(1)闭合开关S前,将滑动变阻器R1的滑片滑到b端.将温控室的温度设置为T,电阻箱R0调为某一阻值R01,闭合开关S,调节滑动变阻器R1,使电压表和电流表的指针偏转到某一位置.记录此时电压表和电流表的示数T和R01,断开开关S.再将电压表与热敏电阻C端间的导线改接到D端,闭合开关S.反复调节R0和R1,使电压表和电流表的示数与上述记录的示数相同.记录此时电阻箱的阻值R02,断开开关S.
(2)实验中记录的阻值R01______R02(选填、“小于”或“等于”).此时热敏电阻阻值RT=______.
解析:求热敏电阻是该题的难点部分,只要能识别出实验原理就很容易突破.抓住题干中“将C端改接到D端,使电压表和电流表的示数与上述记录的示数相同”这段表述,将电压表对应“U”,电流表对应“I”,热敏电阻对应“R”,可借助“UIR三角模型”中“UI-R”思维方式可知前后两次电阻相同,若用RA表示电流表的内阻,可写出前后电阻的关系式
RA+R01=RA+R02+RT
求得
RT=R01-R02
显然R01大于R02.
【例2】(2021年高考理综全国乙卷第23题)一实验小组利用图12所示的电路测量一电池的电动势E(约1.5 V)和内阻r(小于2 Ω).图中电压表量程为1 V,内阻为RV=380.0 Ω;定值电阻为R0=20.0 Ω;电阻箱R,最大阻值为999.9 Ω,S为开关.按电路图连接电路,完成下列填空:
(1)为保护电压表,闭合开关前,电阻箱接入电路的电阻值可以选______Ω.(填“5.0”或“15.0”);
(2)闭合开关,多次调节电阻箱,记录下阻值R和电压表的相应读数U;


图12 例2题图
解析:第一步,用“UIR三角模型”中“UR-R”思维方式处理,电压表(V)示数不能超过1 V,而电压表内阻与定值电阻的并联值R为19 Ω,电阻箱要分担至少0.5 V的电压,若忽略电池内阻的分压(不影响结论),据串联电路分压与电阻成正比,电阻箱阻值R至少应为9.5 Ω,显然5.0 Ω不符合要求,15.0 Ω符合要求.第三步,电路设计里边没有电流表,只有电压表(V)和电阻R,要使用闭合电路的欧姆定律列方程,必须表示出电流I,可用“UIR三角模型”中“UR-I”思维方式处理.用电压表示数U及电压表内阻与定值电阻的并联值R并表示出闭合电路的电流I.
(1)
再用“UIR三角模型”中“IR-U”思维方式得出电阻箱及内阻上的电压URr为
URr=I(R+r)
(2)
再用“UIR三角模型”中“UU”思维方式表示出电动势E和电路中各部分电压关系式为
E=URr+U
(3)
联立式(1)~(3)得
(4)
本题的综合性较强,综合运用了“UIR三角模型”中的多种思维方式联合求解.
4 结束语
综上可知,“UIR三角模型”蕴含着丰富的思维方式,是解决灵活多变的高考电学实验题目的有力武器.它能使学生洞悉命题思路,快速掌握关键点,理清解题思路,方便学生调用所学电路知识和规律快速解答.在日常实验教学中,教师应重视物理建模教学,培养学生的建模、用模意识,使学生养成根据具体物理问题,利用所学知识综合运用多种思维方式进行模型构建,并在此基础上推理、分析问题.以此优化学生的思维结构,提升科学思维品质,发展学生的物理学科核心素养.

