多尺度PCA-HOG遥感异源图像匹配算法 *
韩松来,王钰婕,王 星,罗世彬,董 晶
(1. 中南大学 航空航天学院, 湖南 长沙 410083; 2. 复杂系统控制与智能协同技术重点实验室, 北京 100074;3. 国防科技大学 空天科学学院, 湖南 长沙 410073)
由于成像的物理机制不同,异源图像可反映出地物的不同特性,并通过各类信息的互补获得更加完整的图像信息。遥感异源图像匹配是各类遥感信息处理和视觉导航应用中的关键技术之一[1-5]。一方面,由于成像传感器的差异,异源图像之间存在复杂的非线性灰度畸变,这会严重降低相同对象在不同图像间的相似性;另一方面,遥感图像可能因传感器或传输引入强噪声干扰,对图像信息产生严重破坏,以光学影像和合成孔径雷达(Synthetic Aperture Radar,SAR)影像为例(如图1所示)。因此,尽管图像匹配经过了长期广泛的研究,遥感异源图像匹配仍然是一项极具挑战的难题。
1 相关研究

(a) 光学影像(a) Visible image (b) SAR影像(b) SAR image图1 噪声干扰和非线性灰度畸变Fig.1 Noise corruption and nonlinear gray distortion
图像匹配可以分为基于局部特征的匹配方法和基于模板的匹配方法。基于局部特征的匹配方法首先对图像提取局部特征,然后生成局部特征描述,再进行特征匹配,最后根据特征对应关系计算图像的全局变换得到匹配结果。由于有效地利用了特征的不变性,并能适应尺度和视角变化,基于局部特征的图像匹配方法在计算视觉领域中得到了广泛应用[6-8]。然而,遥感异源图像之间存在强噪声干扰和复杂的非线性灰度畸变,这会导致局部特征发生严重变化,从而无法在图像间检测到足够多的重复局部特征,并且变化也使得正确匹配局部特征变得非常困难[9-11]。尺度比不变特征变换算法(Scale Invariant Feature Transform, SIFT)是一种经典的局部特征匹配算法。图2使用SIFT对遥感SAR和可见光图像进行匹配,可以看到几乎所有的局部特征都匹配错误。

图2 基于SIFT特征的遥感SAR(左)与可见光(右)图像匹配Fig.2 Remote sensing SAR (left) and visible light (right) image matching based on SIFT feature
基于模板的匹配方法也可以称为相关匹配方法,它将模板图像与基准图像上每个候选位置区域的图像进行比较,并选择具有最大相似性系数或最小差别系数的对应位置作为匹配结果。直接基于灰度的模板匹配很难有效适应复杂的非线性灰度畸变,但是利用结构特征描述图像信息可以改善这个问题,因为结构的几何信息能对灰度畸变保持不变。并且,基于模板的匹配方法可以利用密集描述(每个像素都提取)最大限度地提取图像的所有结构特征信息,而基于局部特征的匹配方法往往是基于稀疏的特征对应,因此前者往往具有更强的可靠性。相关研究中的比较测试结果表明,基于模板的匹配方法比基于局部特征的匹配方法能更有效地适应强噪声干扰和复杂的非线性灰度畸变,从而能更有效地匹配遥感异源图像[9-11]。
为了适应异源图像间的复杂非线性灰度畸变,一些模板匹配算法对相似性或差别度量准则进行了改进[12-13]。归一化互相关(Normalized Cross Correlation, NCC)是一种图像匹配常用的相似性度量方法,它能对图像间的线性灰度畸变保持不变,并且因为图像间的单调非线性灰度变化通常是局部线性的,对这种情况,其也能有效匹配图像[14]。然而,当图像间发生非单调非线性的灰度畸变时,NCC可能无法正确匹配图像[15]。对此,Hel-Or等提出了一种基于色调映射(Matching by Tone Mapping, MTM)的图像匹配方法[14],该方法可以看作是NCC的非线性范化,而NCC是该方法的线性简化版。MTM匹配方法的计算时间与NCC接近,但是能有效适应图像间的非单调非线性灰度畸变。MTM仍然需要假设图像间的灰度畸变满足函数映射关系,但是异源图像间的灰度畸变通常不满足这种关系。互信息(Mutual Information, MI)是一种常用的异源图像匹配相似度度量方法。MI通过计算两幅图像之间的统计相关性来确定相似性,它不需要图像间的灰度畸变满足函数映射关系[16]。根据相关研究,MI比NCC和MTM具有更好的异源图像匹配性能[13]。但是在实际使用中,MI匹配方法往往存在匹配搜索计算量过大和参数敏感问题[12]。
仅仅改进匹配的测量准则并直接对灰度图像进行匹配,效果往往不太理想,这样忽略了图像的纹理结构信息。鉴于此,一些模板匹配算法先使用结构特征描述提取图像中的纹理结构信息得到本征图像,然后再对本征图像进行匹配。
方向梯度直方图(Histogram of Oriented Gradients,HOG)利用梯度的方向和归一化梯度强度来描述图像的结构特征[17],它可以很好地适应光照和对比度变化,在图像匹配中经常使用。但是,HOG描述基于图像梯度,因此对图像噪声比较敏感。局部自相似(Local Self Similarity, LSS)描述[18]和稠密自适应自相关(Dense Adaptive Self-Correlation, DASC)描述[19]都利用自相关系数的变化来提取图像的结构特征,可以有效适应非线性灰度畸变,但是因为相关系数对噪声也非常敏感,这两种方法都很难用于遥感异源图像匹配。Kovesi[20]提出的相位一致性模型可以捕获图像的结构幅值,该模型对灰度畸变能较好地保持不变性,并且不容易受噪声影响,但是结构幅值没有方向性,因此它包含的图像结构信息比较有限,这不利于匹配中区分重复模式。因此,Ye等扩展了相位一致性模型,提出了相位一致性直方图[21](Histogram of Orientated Phase Consistency, HOPC)。他们利用Log-Gabor奇对称小波计算相位一致性的方向,并根据相位一致性的方向和幅值构造描述子。他们的实验表明:相比于MTM、MI和NCC,HOPC能更可靠地匹配遥感异源图像。
基于模板的匹配方法还存在搜索过程计算量太大的问题。全搜索的模板匹配是一种逐像素的匹配,特别是对复杂的全局变换(如透视变换、仿射变换),搜索时要考虑平移、缩放、旋转等多个维度。当搜索空间维度加大,全搜索计算复杂性会呈指数级增长。而基于局部特征的匹配算法只要在特征集里搜索,特征描述的维数远远低于图像维数,并且不需要在图像变换空间搜索,所以计算速度优势明显。但是如果图像在匹配前经过校正,消除了缩放、旋转、仿射、透视等变形,则模板匹配可以只做平移搜索,从而能大大减少计算量,经过搜索优化的模板匹配算法的计算速度往往快于基于特征的图像匹配算法[22]。但是对于一些实时应用,平移搜索的模板匹配计算量仍然需要进一步优化。
针对遥感异源图像匹配存在的问题,本文提出了一种基于主成分分析(Principal Component Analysis,PCA)增强的HOG特征描述的快速图像匹配算法(PCA-HOG),并在实验部分对该算法的匹配准确率与计算效率进行了验证。
2 基于PCA-HOG描述的结构特征提取
2.1 传统HOG算子描述
HOG[17]是目标检测和图像匹配中常用的特征描述子。HOG通过统计局部梯度强度和方向构成直方图,并对图像的结构特征进行描述。HOG特征与图像的整体灰度变化相独立,因此对于异源图像存在的非线性辐射畸变,HOG能保持良好的不变性。HOG特征的提取主要分成以下几个步骤:
1)使用Sobel或Laplacian梯度算子与图形进行卷积,得梯度图像。
2)按照图3,将方向分成8个bin,并对梯度按照方向进行统计,得到8维的直方图。
3)对直方图进行归一化处理,降低灰度畸变引起的梯度强度变化。
4)一个局部特征区域可以分成若干个block,每个block又可以分成若干个patch,每个patch可以按照步骤2统计得到一个8维直方图,然后进行拼接得到最终的HOG描述。若一个block有16个patch,那么它对应的HOG描述就是128维。
可见HOG描述是基于局部梯度而形成的,而梯度方向对于噪声干扰十分敏感[23]。由于HOG描述是按照梯度方向进行统计得到,它的抗噪声能力并不强,对遥感异源图像的匹配正确率不高。

图3 HOG的方向划分Fig.3 Orientation division of HOG
2.2 PCA增强的HOG特征描述
为了使HOG特征描述更好地适应噪声,可利用PCA对图像的梯度方向进行增强,然后再按增强后的梯度方向统计得到HOG描述。本文提出的PCA-HOG描述的计算主要分成3个步骤:首先,使用 Sobel算子计算图像梯度Gx与Gy,然后对梯度Gx、Gy进行多尺度PCA增强计算,最后按照梯度方向统计计算HOG描述。其中第一个步骤和最后一个步骤与传统HOG算子的计算没有区别。PCA增强计算可以分成基于奇异值分解(Singular Value Decomposition,SVD)和基于梯度求和的两种方法。
2.2.1 基于SVD的 PCA计算
PCA常被用于计算给定数据集的优势向量。因此,可以利用PCA对图像局部梯度处理,计算出局部梯度主向量,其方向即是局部主方向。主方向比原来的梯度方向更加稳定,不容易受到噪声干扰。图4(a)给出了直接利用Sobel算子计算的梯度方向,图4(b)给出了使用SVD计算的PCA提取的主方向,可见在噪声干扰下,主方向能更加准确地提取图像中结构纹理的方向。

(a) Sobel直接提取的梯度方向(a) Orientation maps estimated with Sobel

(b) SVD的PCA提取的梯度方向(b) Orientation maps estimated with PCA used SVD

(c) 多尺度梯度求和的PCA提取的梯度方向(c) Orientation maps estimated with PCA used method of multi-scale gradients summation图4 提取图像局部方向的对比Fig.4 Comparison of the image local orientation extraction methods
对于给定图像I中的一个像素点(x,y),在N×N的邻域内,其垂直与水平方向的梯度可以构成一个大小为N2×2的局部梯度矩阵G:
(1)
对G矩阵进行SVD分解:
G=USVT
(2)

2.2.2 PCA计算的多尺度梯度求和法

(3)
式中,∑表示对i×i邻域进行求和,尺度i决定了邻域范围大小。 最终的主方向计算是基于多个尺度平均梯度的加权融合计算得到的Gxx、Gyy、Gxy:
(4)
式中,权值wi的定义如下:
(5)
最后像素点的主方向φ计算方法如下:
(6)


(7)
图4(c)给出了使用多尺度梯度求和计算的主方向,可见多尺度梯度求和计算的主方向与SVD计算的主方向(图4(b))基本一致,都对噪声干扰有良好适应性,但是梯度求和法的计算量要比SVD少,并且可以通过积分图像优化进一步减少计算量。
3 匹配算法的实现与加速方法
3.1 基于多尺度PCA-HOG描述的模板匹配算法
本文提出的匹配算法是一种全搜索的模板匹配算法,算法计算模板与基准图上候选窗口之间的相关性,并逐像素地移动候选窗口以寻找最佳匹配目标窗口。图5所示为全搜索模板匹配的示意。这种全搜索方法是假设图像已经进行了几何校正,模板和基准图之间只存在平移变换,这样的全搜索匹配算法常常在视觉导航和制导领域使用。

图5 全搜索模板匹配示意Fig.5 Diagram of full-search template matching
设A={a(x1,y1),a(x2,y2),…,a(xn,yn)}为模板窗口,大小为n×n;基准图为B={b(α1,β1),b(α2,β2),…,b(αm,βm)},大小为m×m。则所提出的模板匹配方法可以定义为如式(8)所示的最优化问题:
(8)
式中:P代表匹配输出的位置结果;Ii为基准图B上候选窗口,Uw为基准图B上候选窗口的集合;T(·)表示将灰度图像转换为PCA-HOG特征向量;D(·)为两特征向量之间的相似性度量函数,本文使用NCC[9]作为相似性度量函数。

图6 算法流程Fig.6 Flowchart of the proposed algorithm
算法的整体流程如图6所示,关键步骤包括:
1)使用Sobel算子提取x与y方向的图像梯度Gx与Gy。
2)利用PCA计算每个像素的局部主方向。
3)利用主方向与梯度幅值计算PCA-HOG特征。
4)利用快速傅里叶变换(Fast Fourier Transform,FFT)加速的NCC计算模板与基准图中候选窗口之间的相似性系数。
5)输出相似性系数最大的候选窗口位置作为匹配结果。
3.2 算法加速
计算效率优化可以使用金字塔策略或者基于梯度下降的搜索优化策略,但是这样的优化方法与全搜索方法不等价,可能错失最优结果。本文对算法计算效率进行了两方面的改进,能够在与全搜索方法等价的条件下(确保不遗漏最优结果)大幅提升计算速度。
1)使用积分图像对基于梯度求和的PCA计算进行加速。
2)FFT对NCC相似性系数计算进行加速。
3.2.1 积分图像加速PCA
积分图像中每个像素的值是从图像原点(左上角)到这一点所构成矩形内所有像素值的和[24]。因此,图7中,原图像矩形区域内的像素值之和sum可以按照下式求得:
sum=s3-s2-s4+s1
(9)
式中,s1、s2、s3、s4是矩形区域4个角位置对应在积分图像上的像素值。因此无论矩形区域大小,使用积分图像求和都只需要三次加法计算。对于大小为M×N的图像,从原图像得到积分图的计算复杂性为O(M×N)。所以如果需要对图像上很多矩形区域求和,并且矩形区域较大时,积分图像求和方法可以节省大量计算。
梯度求和法的PCA计算的主要计算量为每个像素的邻域梯度求和。本文利用积分图像对式(3)中的局部梯度进行求和。假设邻域矩形大小为5像素×5像素,则直接求和的计算量约为25×M×N,而使用积分图像求和的计算量约为4×M×N,计算速度能提高5倍多。

(a) 原图像(a) Original image (b) 积分图像(b) Integral image图7 基于积分图像求和Fig.7 Summation based on integral image
3.2.2 FFT加速NCC相似性计算
卷积定理可以利用FFT对卷积过程进行加速[22]。假设卷积操作中的基准图大小为m像素×m像素, 模板大小n像素×n像素,若搜索时确保模板包含在基准图内,则在空间域直接计算卷积的复杂度为O((m-n+1)2n2),而使用FFT加速后的卷积计算复杂度为O(2m2log2m)。比较可以发现,当模板较大时,使用FFT加速后的卷积可以大幅减少计算量。NCC的计算公式如下:
(10)

4 实验结果及分析
4.1 数据集
使用20对遥感异源图像对提出的算法和现有的模板匹配算法进行比较测试。测试图像包括SAR、红外、激光雷达和可见光图像。图像中的地物类型主要包括:城市建筑、道路、桥梁、河流和山脉等。图8给出了一些测试匹配对的例子,可见这些遥感异源图像之间存在严重的灰度畸变,并且SAR图像还存在严重的噪声畸变和细节缺失,这些都给图像匹配带来了很大的困难。

(a) 可见光图像与红外图像对比(a) Comparison between visible image and infrared image

(b) 可见光图像与激光雷达图像对比(b) Comparison between visible image and laser radar image

(c) 可见光图像与SAR图像对比(c) Comparison between visible image and SAR image图8 测试集图例Fig.8 Samples from testing data
每一对异源图像都包括实时图像和基准图像,从实时图像中选取模板匹配到基准图上。选取的模板分为4种不同的大小,分别为32像素×32像素、64像素×64像素、96像素×96像素、128像素×128像素。对于各尺度的模板,在实时图内随机选取25个模板。基准图像的尺寸都是320像素×320像素。此外,对测试图像进行归一化处理后添加了三种不同方差(0.01,0.03,0.05)的高斯噪声来测试算法的抗噪声能力。图9给出了原图像和添加噪声图像的例子,其中图9(a)为原图像,图9(b)~(d)添加了不同方差的高斯噪声。


图9 噪声示例Fig.9 Noise samples
4.2 评价标准
使用匹配正确率(Correct Matching Rate,CMR)作为算法表现的评价标准。CMR=CM/R,其中R是总匹配对次数,CM是匹配正确的次数。在本文,当匹配位置与实际位置重叠面积比(Overlapping Area Ratio, OAR)达到90%以上时,匹配结果被认定为正确的。
(11)
式中:TW为模板的边长;Δx、Δy为匹配位置和实际位置的误差;f(x)为截断函数,

(12)
4.3 算法比较结果与分析
本节通过与现有算法MI[16]、基于方向梯度通道特征(Channel Features of Orientated Gradients,CFOG)的模板匹配算法[12]、HOG-NCC、HOPC[21]的实验结果相比较,来分析所提算法PCA-HOG在遥感异源图像匹配中的优越性。下面简要介绍以上算法:
1)CFOG:是一种基于图像方向梯度的像素化特征表示,是对HOG特征描述符的扩展,基于CFOG的模板匹配具有优越的计算效率,但是因为CFOG直接基于梯度构建,存在对噪声适应性不足的问题。
2)HOG-NCC:该匹配算法使用HOG作为特征描述,并使用NCC作为相似度度量方法。相比于本文算法,HOG-NCC并没有使用PCA提取主方向,也没有使用积分图像和FFT加速方法。
3)HOPC:该算法先使用log-Gabor提取方向,然后按方向统计相位一致性,得到相位一致性直方图特征,最后使用NCC作为相似性度量进行匹配。HOPC利用了图像的相位信息,但是相位对噪声干扰也比较敏感。
图10显示了对原图像(没有添加噪声),各种算法使用不同大小模板的匹配正确率。结果表明本文提出的匹配算法PCA-HOG整体高于其他几种匹配算法,平均正确率高出第二名(CFOG)3.5%。另外可以看出,基于结构特征的匹配算法(CFOG、HOPC、PCA-HOG、HOG-NCC)的正确率都相比于直接基于图像灰度的匹配算法(MI)高。这一结果表明,对于非线性灰度畸变非常明显的遥感异源图像,直接对图像灰度进行相似性度量的匹配算法不是非常有效,应该使用特征描述先提取结构信息,然后再匹配。
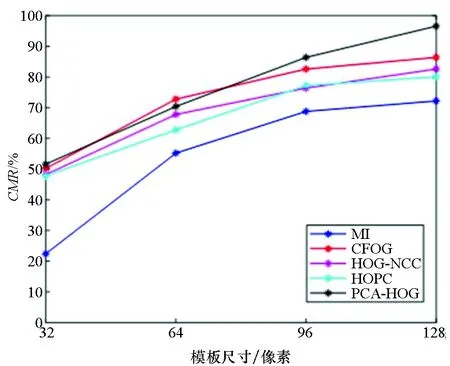
图10 原图像匹配结果Fig.10 Matching result on original images
此外,对测试算法在不同程度噪声干扰下的结果进行了比较,结果如图11所示。可以看出,所有算法的CMR都随着噪声水平的增加而降低,而PCA-HOG相较于其他几种算法,整体匹配正确率更高。另外,随着噪声强度的增加,相比于基于图像灰度的算法(MI),基于结构特征的算法(CFOG、HOPC、PCA-HOG、HOG-NCC)正确率下降得都更快。尤其是当高斯噪声方差为0.05时,一些基于结构特征的匹配算法正确率要小于MI。这是因为这些算法的结构特征提取方法都是基于梯度或相位,梯度或相位对噪声干扰非常敏感。PCA-HOG算法的匹配正确率明显优于HOG-NCC算法,后者没有使用PCA提取主方向,这验证了使用PCA对HOG特征增强可以改善匹配性能。
图12给出了部分PCA-HOG匹配结果图,其中的SAR图像带有严重的噪声,且和可见光图像、红外图像间有着很大的灰度差异,使用PCA-HOG算法仍然可以正确匹配图像,这说明该算法能有效匹配带有灰度畸变和噪声干扰的遥感异源图像。

(a) 模板尺寸: 32像素×32像素(a) Template size: 32 pixel×32 pixel

(b) 模板尺寸: 64像素×64像素(b) Template size: 64 pixel×64 pixel

(c) 模板尺寸: 96像素×96像素(c) Template size: 96 pixel×96 pixel

(d) 模板尺寸: 128像素×128像素(d) Template size: 128 pixel×128 pixel图11 添加噪声情况下测试算法的匹配结果Fig.11 Matching results of tested algorithms on images with noise

(a) SAR-可见光(将SAR图像叠加到可见光图上)(a) SAR-visible (bottom layer is visible image; top layer is SAR image)

(b) SAR-红外(将SAR图像叠加到红外图像上)(b) SAR-infrared (bottom layer is infrared image; top layer is SAR image)图12 PCA-HOG算法的匹配结果示例Fig.12 Samples of PCA-HOG matching results
对提出的算法加速方法也进行了测试。测试平台为Intel CPU i7 单核2.10 GHz,对使用加速方法和不使用加速方法的PCA-HOG算法的运行时间进行了测试,结果如表1所示,其中基准图尺寸为320像素×320像素。

表1 算法运行时间比较
从表1可以看出,在使用加速方法的情况下,算法的运行速度有1~2个数量级的提升,这与本文3.2节对算法复杂性的分析基本一致。
5 结论
针对遥感异源图像匹配存在的问题,提出了一种基于PCA增强HOG特征描述的快速遥感异源图像匹配算法。该算法利用PCA对局部主方向进行提取,改进了HOG描述对噪声的适应性。实验对算法在遥感异源图像数据集上进行了评估,并且与现有的算法进行了比较。实验结果表明,本文提出的匹配算法在正确率上明显优于其他测试算法。本文算法还利用积分图像对特征提取过程进行加速,并使用FFT对匹配搜索过程进行了加速。实验部分,对比了加速前后的匹配算法,测试结果表明加速方法能将算法的计算效率提高1~2个数量级。本文提出的匹配算法和其他4种比较的算法都是按照整像素平移搜索实现的模板匹配算法,因此,不能实现亚像素匹配定位。后续将对基于本算法的亚像素精确匹配开展研究。

