基于滑模自适应鲁棒控制的四旋翼飞行器轨迹跟踪*

杨明博，周紫阳，戴 峻，游翔茗

（1.北方工业大学机械与材料工程学院，北京 100043；2.煤炭科学技术研究有限公司，北京 100020）

0 引言

在21 世纪的今天，随着人们对自动控制领域和传感技术领域的深入研究，融合这两部分技术的无人机飞行器成为了一个专门的研究领域。在无人机飞行器领域中，四旋翼飞行器自身结构简单，能够实现自由悬停和垂直起降等运动方式，实际应用中操作简单，能够克服恶劣环境到达一些特殊的区域，引起很多学者的关注［1-2］。

关于四旋翼飞行器的轨迹跟踪控制，学者们提出了不同的控制方法。其中在实际中经常应用的控制算法有PID 控制［3-4］、滑模控制［6-7］、自适应控制［8-9］、反步控制［10］等。在众多控制算法当中，PID 控制算法无论是在工业还是民用中都被广泛使用。PID 算法能通过调节3 个环节的参数使系统达到稳定，但是寻找合适的参数是非常复杂的过程，工作量非常大。文献［5］中就是采用PID 控制算法进行位置和姿态信息的轨迹跟踪：通过对反馈信号的分析研究和基于PID 算法的控制器设计，跟踪到四旋翼飞行器的飞行轨迹。但是调节参数的过程复杂，并且所设计的控制器在面对更高的飞行要求和较快的速度下跟踪精度会受到影响。文献［11］中提出了一种自适应控制算法来进行轨迹跟踪，将四旋翼飞行器分解为位置、欧拉角和角速率3 个动态子系统，并结合欠驱动约束分别设计虚拟控制器，简化控制器的设计。虽然文中的自适应控制算法能够抑制扰动对四旋翼飞行器稳定性的影响，但是还需要设计低通滤波器和不确定性补偿器，使整体控制变得繁琐。文献［12］中采用反步控制方法，通过引入跟踪误差的积分项，降低飞行器进行轨迹跟踪时的稳态误差。然而并没有考虑在强风等扰动条件下对跟踪精度的影响，系统没有显示出很好的鲁棒性。文献［13］中提出了一种基于切换函数的扩张状态观测器设计方法，来对系统中的扰动进行估计，并将估计值与滑模控制器的设计相结合，实现轨迹跟踪控制。但是在滑模控制中会产生抖振现象，影响控制精度。

相比其他方法需要设计观测器或者是多次调整参数来抑制扰动从而达到控制要求，本文结合了内外环控制的思想，分别以自适应扰动为主体和滑模函数来设计控制器。本文中还考虑了四旋翼飞行器负重时质量改变对系统稳定性的影响，证明了滑模自适应算法在负重的情况下稳定性不被破坏，拥有较好的鲁棒性。在对干扰的抑制和提高控制精度方面以及调整参数的过程更加简易。

1 四旋翼飞行器动态模型

1.1 坐标系的建立

本文引入机体坐标系和惯性坐标系来描述飞行器的转动和位置姿态，机体坐标系记为A（Ax，Ay，Az），惯性坐标系并记为B（Bx，By，Bz），如图1 所示。机体坐标系A 到惯性坐标系B 的转换矩阵RAB。

图1 四旋翼飞行器坐标系建立示意图

1.2 四旋翼飞行器动力学模型

由于四旋翼飞行器主要运动形式分为两种，一种是相对于惯性系B 的平移运动，另一种是相对于机体坐标系A 的转动，一共6 个自由度。于是可根据总的自由度数确定广义坐标为q=（ξ，η）T，其中ξ=［x，y，z］T表示位置信息；η=［γ，θ，ψ］T表示姿态信息。飞行器的质量为m，重力加速g，飞行器旋翼末端到飞行器重心的距离为l。四旋翼飞行器在机体坐标系下的惯性矩阵为：

Ix，Iy，Iz分别代表在A 坐标系下X 轴、Y 轴和Z轴的转动惯量，可以通过测试得出。

四旋翼飞行器的位置部分表述方程如下所示：

系数C 是科里奥利力及离心项［15］，具体表示为式（5）［16］。

2 控制器设计

本文的控制策略，总体设计方案如图2 所示。

图2 四旋翼飞行器控制系统结构图

2.1 位置跟踪控制器设计

位置控制器的主要设计思路是将理想的位置轨迹和实际的位置轨迹进行比较，最后让两个的误差趋近于零。于是可将期望跟踪的位移轨迹设为ξc，实际跟踪得到的位移量记为ξ。将误差设为es并且es=ξ-ξc。

于是根据式（2）可以将ξ··单独表示出来，然后对误差表达式两边求两次导数，如下形式：

式（6）中，us=u1RABe3是需要进行设计的控制输入量，可以将us理解为一种虚拟控制律，作为一种坐标变换的中间量来理解。

根据滑模自适应鲁棒控制方法，首先进行滑模函数的设计。可将滑模函数设为如下形式：

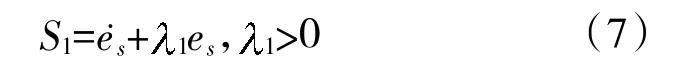
设计位置子系统的虚拟控制律us为：

将上面的误差es求导数，代入得：

本文不同于其他方法在于针对四旋翼飞行器系统中，由于位置运动部分主要是要减小干扰力矩对运动轨迹的影响，故设计干扰力矩作为自适应律，让其更好地进行位置轨迹跟踪。同时为了体现出控制方法的优越性，考虑飞行器负载时导致质量的变化，进而影响四旋翼飞行器的升降动力和稳定性，故将质量也设计自适应律。

将自适应律定义为如下形式：

式中，γ1和γ2均为控制系数。

定义位移部分的干扰力误差量为：eds=ds-d^s；质量误差量为：em=m-m^。

定义李雅普诺夫函数并求导得：

当m^大于限制范围的最大值时，并且处于一直增加的状态，此时m^保持不变即m^·等于0。当m^低于限制范围的最小值时，并且处于一直递减的状态，此时m^保持不变，即m^·等于0。映射自适应算法不仅能保证m^·等于0，还能保证V˙1≤0。

在虚拟控制律us能够被计算出来的情况下，还要将四旋翼飞行器实际的升降动力u1和姿态子系统的中3 个姿态角信号量的总和ηs计算出来。于是可将虚拟控制输入量us表示为：［uxuyuz］T，中间量ηs表示为如下形式：［γsθsψs］T。

因为us=u1RABe3，对us进行矩阵运算表示为如下形式，进一步整理可得x，y，z 方向的动力输入表示。

可得俯仰角和横滚角的表示为：

俯仰角信号量θs和横滚角信号γs是为了跟踪参考位置量，由外环部分虚拟控制输入量生成，并且传递给内环部分的姿态子系统，外环部分产生的误差通过内环部分进行消除。偏航角ψs则是作为给定的控制信号，由信号发生器产生。可以在信号发生器设置其输入值来对任意的偏航角进行跟踪。实际的位置控制器输入设计为u1=uz/cosθcosγ，并且u1为实际的控制输入量。

2.2 姿态跟踪控制器设计

姿态控制部分为内环子系统，通过内环控制律实现姿态控制，同时对外环控制产生的俯仰角信号量θs和横滚角信号量γs进行跟踪。在姿态子系统的控制中，主要跟踪的量为ηs，根据上述推导的姿态部分方程表达式可知，姿态部分的控制器主要针对控制量输入转矩进行设计。同时考虑到四旋翼飞行器模型中存在不确定性，以及旋转运动中存在的外界非结构性干扰力矩。于是可将四旋翼飞行器姿态部分的表达式写为如下形式。

其中J=Js+JΔ，C=Cs+CΔ，进一步可将x 方向的干扰力d1表示为与干扰力矩相关的表达式，即d1=dM-JΔη··-CΔη˙，并认为d1是有界量。

所以姿态子系统的动态模型可以表示为：

与位置控制器设计思路相同，首先定义滑模函数，滑模函数S2设为如下形式：

根据定义的滑模函数关系式，可将姿态误差子系统转变为如下形式：

于是可将控制量输入力矩表示为如下形式：

式（34）中，ε 和c2为控制参数，并且要求ε＞dγ，c2＞0。sgn 为符号函数。

从得到的指数趋近律表达式可以看出，当指数趋近速度按照由较大值逐渐缩减到零的规律变化时，此时趋近时间变短，并且保证了目标点趋近切换平面的速度非常小。由于这是一种逐渐逼近的过程，很难保证运动点在确定的时间内到达切换平面［19］，所以在上述基础上添加一个等速趋近项-εsgn（S2）。

定义模型的名义值为：

进一步进行李雅普诺夫函数的构造，具体设计为如下形式：

对V2求导函数可得：

将控制量带入后，整理化简可得：

由此可见李雅普诺夫导函数V˙2为负数，所以李雅普诺夫函数本身特性为单调递减。根据李雅普诺夫稳定性定律可知，可以将姿态子系统部分认为是稳定并且误差是收敛的。

针对整个系统而言，将整体的李雅普诺夫函数定义为：

将V1和V2分别代入后可得：

根据李雅普诺夫稳定性定律可知，整个系统是处于渐进稳定的状态。通过位置控制器得到俯仰信号θs和横滚信号γs后，从式（34）输入转矩的表达式可以看出，还需要将这两个信号量分别求一阶导数和二阶导数。此时是可以通过采用三阶微分器的形式实现对θs和γs一阶导数和二阶导数求取。

3 仿真研究

首先确定参考位置ξs，将参考位置ξs的x 轴、y轴、z 轴的轨迹分别设计为：x=cos（t）；y=sin（t）；z=t。姿态角方面，由于俯仰角和横滚角作为中间指令信号传递给内环控制系统，所以此时只需要定义偏航角即可。将偏航角的常数设定为ψs=π/4。飞行器旋翼末端到飞行器重心的距离为l，取0.5 m。惯性矩阵I 中的参数设为：Ix=0.081；Iy=0.081；Iz=0.141。

位移运动中的干扰力ds取为：

［sin（πt） cos（πt） cos（πt）］T

旋转运动中的干扰力矩dM取为：

由图3 可以看出，轨迹跟踪曲线和理想位置曲线是接近一致的，可以看出提出的控制算法能使系统到达稳定状态，误差在能够控制的范围内。图4～图6 为四旋翼飞行器x、y、z 方向上的误差，反映位置跟踪上的误差。x 方向误差在-0.03～0.07 之间变化，y 方向误差变化范围大致在-0.05～0.06 之间，z方向误差大致在-0.2～0.37 之间变化，三者均是小幅震荡的曲线。由此可以看出，滑模自适应鲁棒控制算法的优越性。

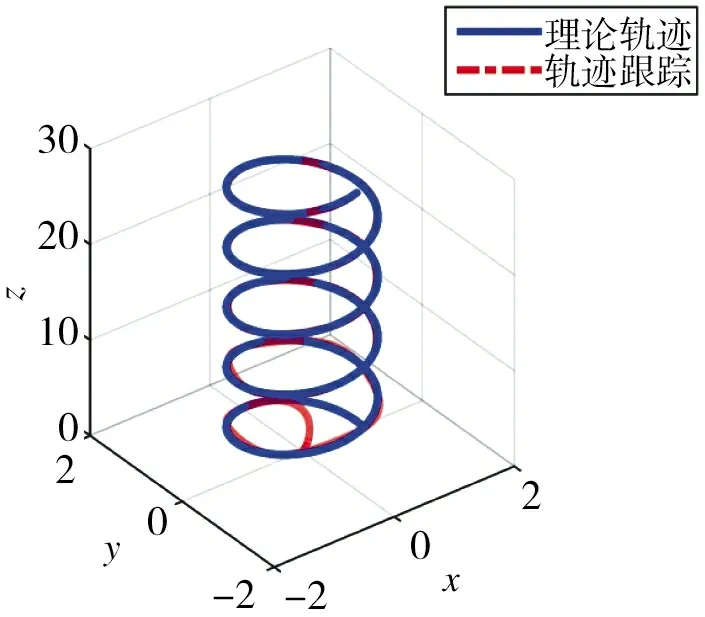
图3 轨迹跟踪效果图

图4 x 方向位置误差

图5 y 方向位置误差

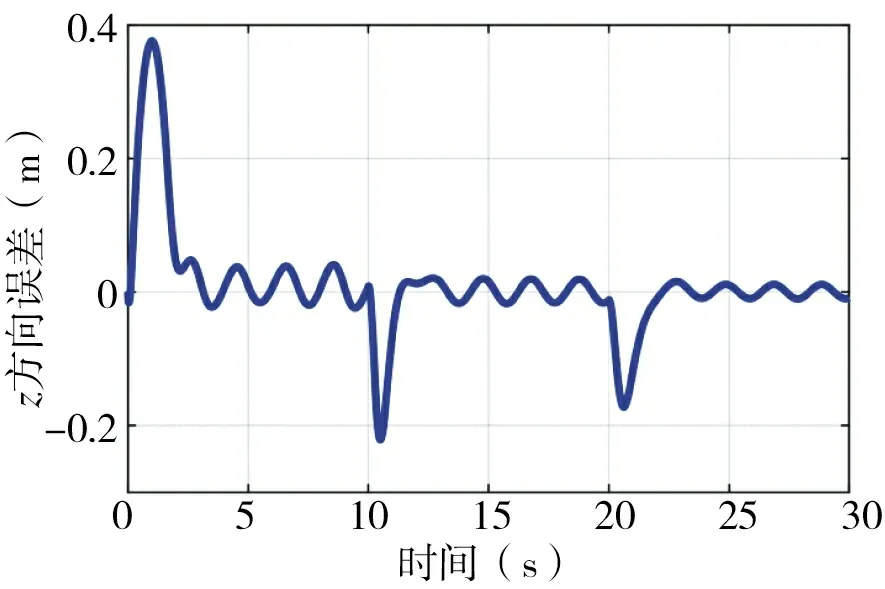
图6 z 方向位置误差

图7～图9 为四旋翼飞行器横滚角、俯仰角、偏航角的轨迹跟踪曲线，可以看出实际的横滚角，俯仰角和偏航角和理想的横滚角，俯仰角和偏航角曲线基本趋于一致。图10 为四旋翼飞行器升降动力即输入量u1的变化，从图中可以看出，升力（输入量）随着质量的变化而变化，并且数值上接近四旋翼飞行器的重力。图11 为质量自适应估计结果，质量估计值和质量实际值曲线大致趋于一致，误差属于允许的范围内。图12 为位置运动部分的扰动力设计值和估计值对比图，可以从图中清晰地看出，x方向和y 方向的干扰力误差基本趋近于零，达到预期目的。z 方向的误差在1～1.5 之间，相比设计的干扰力有明显减小，得到抑制。当质量改变时，能够看出所跟踪的量也随之发生变化，体现出了自适应的特点。从干扰力的前后变化也可以看出这种控制算法的有效性和鲁棒性强的特点。

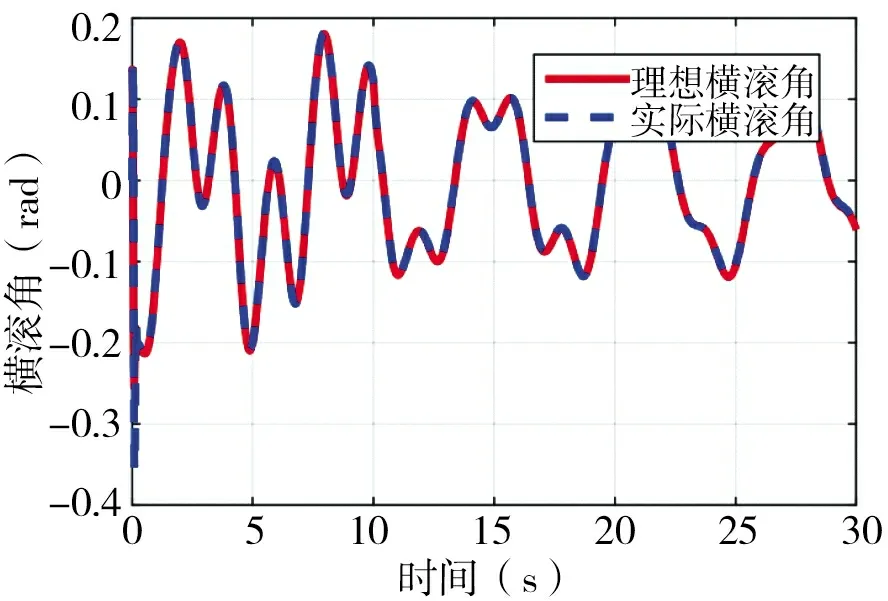
图7 横滚角γ 轨迹跟踪

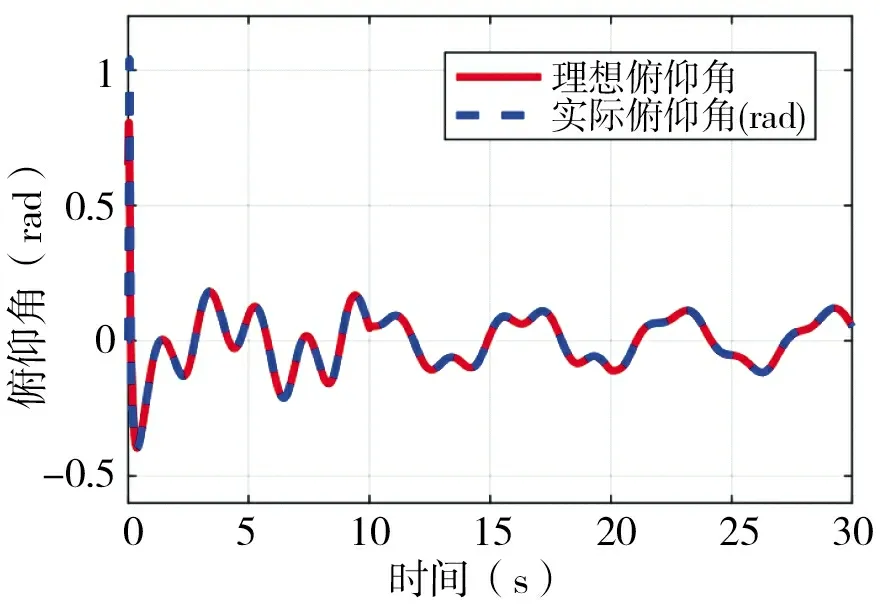
图8 俯仰角θ 轨迹跟踪

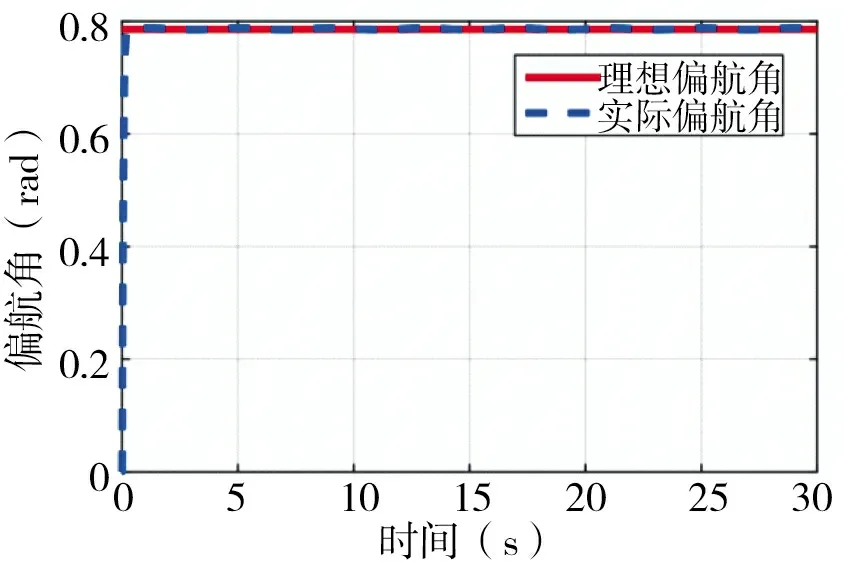
图9 偏航角ψ 轨迹跟踪

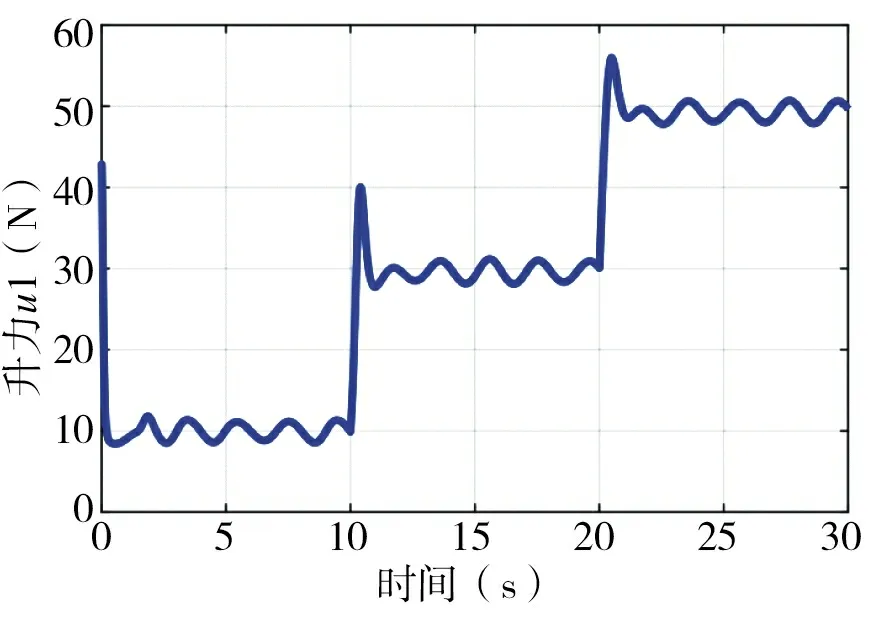
图10 四旋翼飞行器输入量

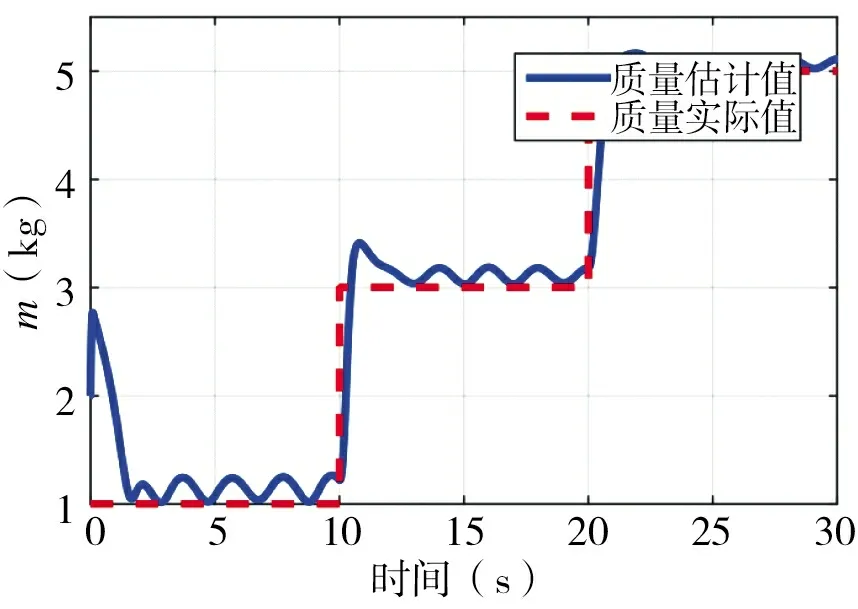
图11 质量自适应估计

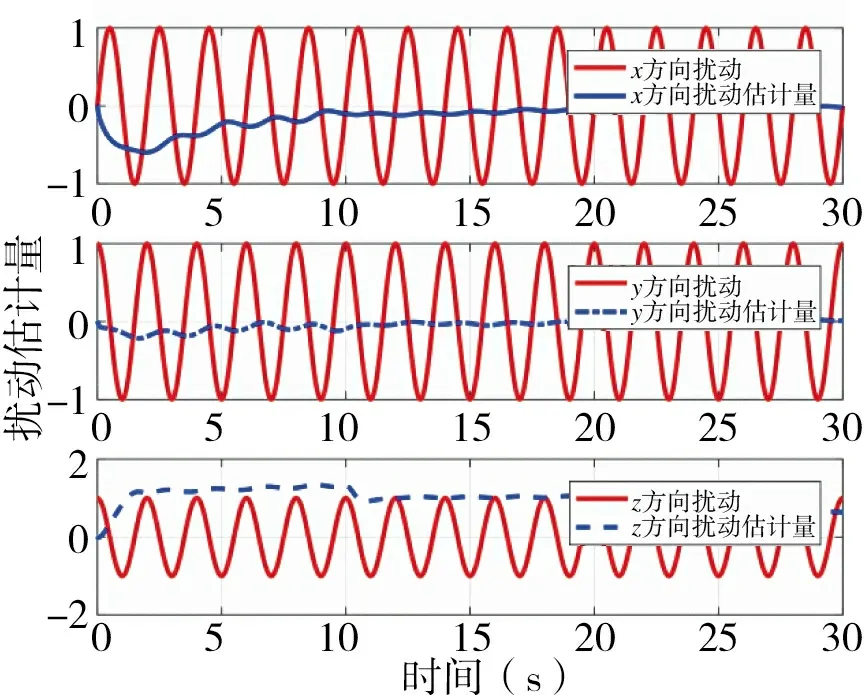
图12 位置方向干扰力自适应估计

通过以上仿真分析研究可以看出，在考虑四旋翼飞行器动态特性及外部扰动和系统不确定性的情况下，滑模自适应鲁棒控制方法设计的控制器能够准确稳定地跟踪给定参考轨迹，获得良好的控制性能，验证了控制算法的有效性。

4 实验研究

为了更好地验证提出控制算法的优越性，本文在实验部分加入经典的PID 控制策略和反步控制方法与本文提出的控制策略进行了对比实验，实验平台如下页图13 所示，实验平台可以实现四旋翼飞行器的悬停和定点飞行。实验平台采用的硬件系统部分为：主控芯片的型号为STM32F427 的PIX 系列飞控；姿态获取部件选择的是MPU6050 传感器；位置参数的测量选择的是型号为M8N 的GPS 模块和MS5611-01BA 气压传感器。实验主要以风作为干扰的情况下，比较四旋翼飞行器的飞行状态，从而验证本文提出控制策略的优越性。

图13 实验平台

实验场地为一般通用的篮球场。实验所设计的轨迹是以篮球场3s 区的罚球线，矩形的具体尺寸为长5.8 m 宽4.9 m，并且在此区域上建立坐标系，如图14 所示。四旋翼飞行器进行轨迹跟踪的实验过程中，首先从原点出发，先垂直起飞一定的高度，高度经自稳后测量为1.2 m，如图15 所示。将四旋翼飞行器按照预先定义好的轨迹在水平方向飞行，本文的实验是让飞行器先后经过（0，0）、（5.8，0）、（5.8，4.9）、（0，4.9），最后回到（0，0）点。采用地面站来接收四旋翼飞行器在飞行中的姿态参数和理论参数进行对比，得到误差范围，以此来证明本文所提出控制算法的优越性。本文所提出的控制策略实验结果如表1 和表2 所示，采用滑模PID 控制算法的实验结果如表3 和表4 所示，反步控制算法结果如表5 和表6 所示。

图14 坐标系建立示意图

图15 实验过程

通过结合表1～表6 的实验数据可以看出，滑模自适应鲁棒控制算法相比滑模PID 控制算法和反步控制算法在稳定时间上更快。虽然作为对照组的两种算法最终也能跟踪到四旋翼飞行器的运动轨迹，但是从跟踪误差上看，两种算法的跟踪误差范围均大于滑模自适应鲁棒控制算法。滑模PID 算法虽然在稳定时间和跟踪精度上能达到不错的效果，但是在调节PID 参数时非常繁琐，参数选取不合适时超调现象严重。由此可以得出结论，在考虑扰动的情况下，通过对比其他两种控制算法的实验结果，滑模自适应鲁棒控制算法稳定性好，精度更高，有明显的优越性。

表1 位置轨迹跟踪指标

表2 姿态轨迹跟踪指标

表3 PID 算法位置轨迹跟踪指标

表4 PID 算法姿态轨迹跟踪指标

表5 反步控制算法位置轨迹跟踪指标

表6 反步控制算法姿态轨迹跟踪指标

5 结论

研究结果表明本文采用的滑模自适应鲁棒控制策略，能很好地实现对四旋翼飞行器既定轨迹的跟踪控制并且保证精度。在对照组的实验研究过程中，体现出了本文研究控制策略的优越性。