基于分治法搜索幻方所有解
丁怡心,廖勇毅
(广州民航职业技术学院,广州 510800)
0 引言
n阶幻方,就是把数字1到n2但放在n×n的正方形格子中,并且要满足每行、每列及两个对角线数字之和相等。

图1 三阶幻方
幻方不但是传统的数学游戏,还被应用到哲学、美术、教育及前沿科学技术中。对于幻方的构造方法有很多,包括针对奇阶幻方的Merzirac法与Loubere法,针对偶阶幻方有Hire法、Strachey法以及YinMagic法。
幻方构造方法的研究目前已非常成熟且成体系[2,3,4,5,6,7,8],然而对于搜索幻方所有解的研究目前尚是空白。要搜索所有解只能通过穷举,对于高阶幻方搜索空间太大,穷举难以实现或是不可能实现。文章研究如何降低搜索空间提高穷举效率。
1 幻方搜索空间
n阶幻方的搜索空间为n2的阶乘,见表1,3阶幻方的搜索空间是362880个,对于现代计算机是可以轻松完成的任务,然而4阶以上幻方的搜索空间开始爆炸式增长,任务变得不可完成。

表1 n阶幻方搜索空间
2 分治穷举法
对于n阶幻方,由于每行数之和相等,所以每行之“和”的值为所有n2个数之和除于n,即:

下面以3阶幻方为例,根据公式(1),3阶幻方每行数之和为15,以此为约束,从9个数中先取3个和为15的数放在第1行,再从剩下6个数中取3个和为15的数放在第2行,剩下的3个数放在第3行。如图2所示,文章称之为候选中间解。

图2 三阶幻方候选中间解
从9个数中取3个放在第1行,再从剩下6个数取3个放在第2行,剩下3个数放在第3行,整个过程产生的组合个数为C39×C36×C33,于是n阶幻方产生的候选中间解数见公式(2)。

然后对候选中间解的每行分别进行全排列,以寻找所有满足n阶幻方条件的解。算法流程如图3所示。

图3 算法盒图
根据公式(2)算得3阶幻方所有组合有1680个。其中满足每行之和相等的候选中间解有12个。
对n阶幻方每个候选中间解的每行进行全排列产生的搜索空间为个见公式(3),则3阶幻方一个候选中间解产生的搜索空间为3!×3!×3!=216,于是总搜索空间为12×216=2592。其中满足3阶幻方要求的最终解有8个。

算法的分治思想体现在把一个规模为n2的阶乘分解成n个规模为n的阶乘,缩小了问题的规模,减小了搜索空间。

图4 三阶幻方所有候选中间解
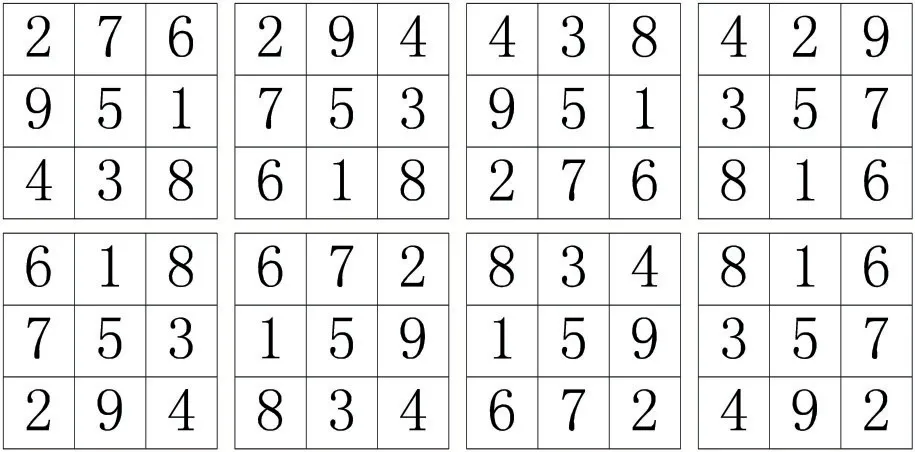
图5 三阶幻方所有解
3 搜索空间对比
根据分治穷举法的算法思想,n阶幻方的搜索空间大小为候选中间解数乘以每个候选中间解产生的搜索空间。其中每个候选中间解产生的搜索空间可由公式(3)算得。

通过表1与表2的对比,分治穷举法极大地缩小了搜索空间。

表2 分治穷举法搜索空间
4 关键代码
算法1递归函数,通过逐行组合获取所有候选中间解。
输入:square方阵二维数组,n幻方维数,line行号。
a)NEXT-COMBINATION(square,n,line)
b) if SUM(square[line])==lineSum
c) if line==n-2
d) NEXT-PERMUTATION(square,0,n)
d) else
e) NEXT-COMBINATION(square,line+1)
f) return
g) NEXT-COMBINATION(square,n,line)
算法2递归函数,通过逐行排列搜索候选中间解的所有最终解。
输入:square方阵数组,start参与全排列的开始位置,end参与全排列的结束位置。
a)NEXT-PERMUTATION(square,start,end){
b)if start==end-1//递归出口
c) if end d) NEXT-PERMUTATION(square,end,end+N) e) else if CHECK-SQUARE(square)==TRUE f) squareCount++ g) PRINT-MAGIC-SQUARE(square) h) return; i)for i=start to end j) SWAP(square,i,start) k) NEXT-PERMUTATION(square,start+1,end) l) SWAP(square,i,start) 使用配置为i5CPU/16G内存的电脑对两种算法的3阶、4阶幻方进行测试,测试结果见表3。 表3 实验数据对比 实验对比表明分治穷举法确实显著提高了搜索效率,而且问题规模越大效果越明显。 对于问题:搜索n阶幻方的所有解。随着n的变大搜索空间出现爆炸式增长,本文提出分治穷举法,把搜索空间从n2的阶乘分解成n个n的阶乘,显著地缩小了搜索空间。并通过实验对比表明分治穷举法极大地提高了搜索效率。5 实验

6 结语

