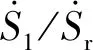利用应力加载速率变化与地震活动性模型探讨2013年吉林前郭震群成因的力学机制
尚园程,史保平
中国科学院大学地球与行星科学学院,北京 100049
0 引言
震群(earthquake swarm)是一类特殊的地震,通常指的是某一特定小区域在较短时间内发生的一系列没有明显主震的中小地震(Scholz,2002).震群的持续时间可以是一些天,几个月,甚至几年.震群中会存在多个震级较大且震级相近的地震,但整个震群的能量释放过程同常见的主震-余震序列由一个主震或几个大震占主导的方式明显不同.主震后发生的一系列余震不应该被称为震群,而震级特别大的多次破坏性地震,一般也不称为震群,比如1976年松潘—平武地区发生的2次7.2级强震和最大震级达6.7级的余震(梁晓峰,2020).理解震群的成因机制目前仍是地震科学的重要挑战.
北京时间2013年10月31日11时3分,在我国吉林省松原市前郭尔罗斯蒙古族自治县发生了MS5.5(ML5.6)地震,震中位置为44.67°N,124.12°E,11时10分,震中再次发生了MS5.0(ML5.3)地震,截至2013年11月23日,吉林前郭—乾安地区共发生MS≥5.0地震5次(吴微微等,2014),最大震级为MS5.8(ML5.6).此次地震是一起典型的板内震群事件(以下简称为前郭震群),其发震构造是一条与长岭—大山子断裂几乎垂直的隐伏断层(李君和王勤彩,2018).前人的研究表明前郭震群的发生与流体的运移有关(Zhang et al.,2019;刘俊清等,2017),但前郭震群的地震发生率相较于2008年9月—2013年9月提高了至少100倍,并且b值(古登堡-里克特定律)出现了明显的降低,现有的研究仍不能对震群出现的这两种现象进行统一的力学机制解释.因此研究前郭震群的成因机制对理解震群的形成机制具有重要的科学意义.
慢滑移是指以几个小时到几个月的时间尺度缓慢发生了有限的断层位错,但没有高频地震波辐射的断层慢滑动事件(吴忠良和许忠淮,2013).近期的研究总结了震群的驱动机制,表明板块内部震群的物理驱动机制主要是慢滑移或流体运移(王鹏,2019).而前人的观测结果还表明慢滑移现象的出现时常伴随着流体运移的发生(Szeliga et al.,2004;Shelly et al.,2006;Schwartz and Rokosky,2007;Audet and Bürgmann,2014),即慢滑移与流体运移有关.但流体运移和慢滑移如何影响断层的演化进而触发震群以及流体运移与慢滑移相关的物理机制仍需进一步研究.
随着岩石物理学实验的发展,前人已对断层演化的物理机制取得了深入的认识,表明地震的演化过程就是断层在不同的时空状态下克服摩擦的过程.基于实验室内岩石实验结果得出的速率-状态摩擦定律(Rate and State Dependent Friction Law,以下简称RSF)已成为定量化研究断层之间的复杂行为的一个基本的框架(Dieterich,1972,1978,1979a,b,1992,1994;Ruina,1980,1983;Rice,1983).
本文将在RSF框架下分析慢滑移和流体运移对断层演化的影响及其触发震群的机制,探讨流体运移与慢滑移之间的相关性,及探讨前郭震群成因的力学机制与其地震发生频率升高与b值减小的可能的原因.
1 理论模型
1.1 速率-状态摩擦定律
速率-状态摩擦定律(简称RSF)是通过对大量岩石摩擦实验结果的总结而得出的,该定律如今已成为研究地震机制和断层演化的有力工具.在RSF中,摩擦系数主要由滑移速率和状态变量θ决定.考虑断层上有效正应力对状态变量的影响,岩石摩擦实验给出(Linker and Dieterich,1992;Dieterich,1992)RSF可表示为:
(1)
(1)式中,τf为断层上的摩擦强度;σ为断层上的正应力;μ为摩擦系数;A与B为摩擦参数;V为断层的滑动速度,V*为参考速度,μ*为V=V*时的参考摩擦系数;Dc为临界滑动位移;θ为考虑正应力影响下的状态变量;α为实验测得的无量纲常数,其取值范围一般为0.2~0.5(Linker and Dieterich,1992).
1.2 1D弹簧-滑块模型
本文采用1D弹簧-滑块模型来类比真实断层,该模型由弹性的弹簧和刚性的滑块组成.其中,弹簧与滑块的接触面代表断层面,弹簧本身则同断层周围的弹性介质及断层或裂纹自身尺度相关,而刚度系数k则与断层面的几何形态有关.根据弹性理论给出的应力-应变关系,断层内部的剪切应力τd的方程可表示为:
τd=τ0+τ-kδ,
(2)
(2)式中,τ0为断层内部的初始应力或剩余应力;τ为外界加载于断层面的剪切应力,δ为滑块的位移;k为单位接触面上的弹簧刚度k≈G/l(Dieterich,1992,1994);其中,G为岩石的剪切模量;l为断层的特征尺度.影响外部加载应力τ的因素可以有很多,比如,远场板块运动、地震波扰动、地下流体扰动、人类活动等等,这些复杂因素综合后共同决定着断层面上的剪切应力状态.
1.3 Dieterich 模型近似解
设定断层在演化过程中始终保持准静态,即断层面上的摩擦力始终等于断层内部的剪切应力.当断层演化处于自加速阶段时,(1)式中的演化方程可近似为(Dieterich,1994):
(3)
将公式(1)中的摩擦定律和(3)式中的状态定律代入(2)式中,我们可以得到关于滑移速率V的演化方程(Dieterich,1994;Dieterich et al.,2015):
(4)
(4)式中,H0=B/Dc-k/σ0>0;S(t)=τ(t)-(μ0-α)σ(t)为修正的库仑应力方程(Dieterich et al.,2015);τ(t)和σ(t)分别为加载于断层上的剪切和有效正应力;摩擦系数μ0≈0.6(Byerlee,1978);S0为断层内部的初始应力,利用公式(4)可以定量研究断层成核过程时滑移速率V同库仑应力变化之间的关联性,其中库仑应力变化可包含静态或动态的应力扰动.与公式(4)相对应的地震发生率R可改写为(Dieterich,1994;Segall and Lu,2015):
(5)
1.4 流体作用下孔隙压力对断层滑移速率的影响
地下流体运移是指岩浆、水、气、油等流体在地下孔隙介质中的流动.地下流体运移可使断层上的孔隙压力升高,进而导致断层面上有效正应力降低.为使问题不失去一般性,本文假设远场加载剪切和有效正应力均随时间呈线性变化,即远场应力加载函数可表示为:
(6a)
(6b)
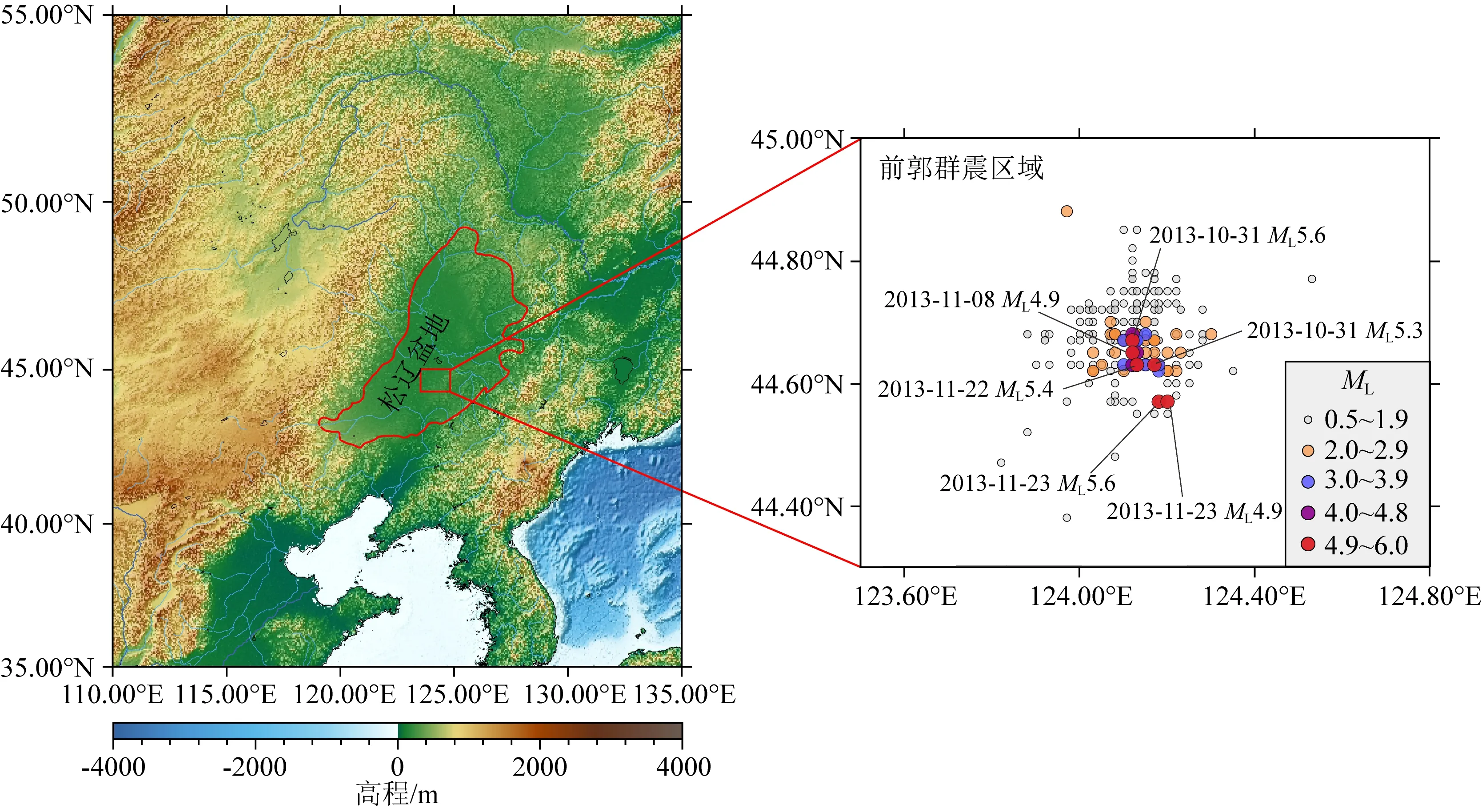
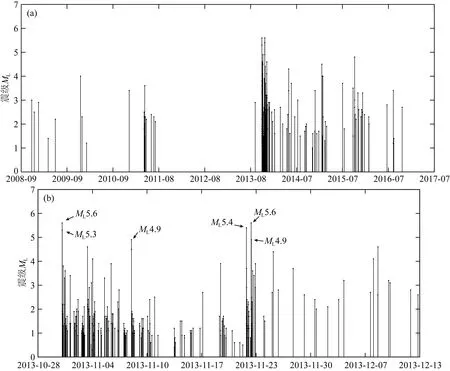
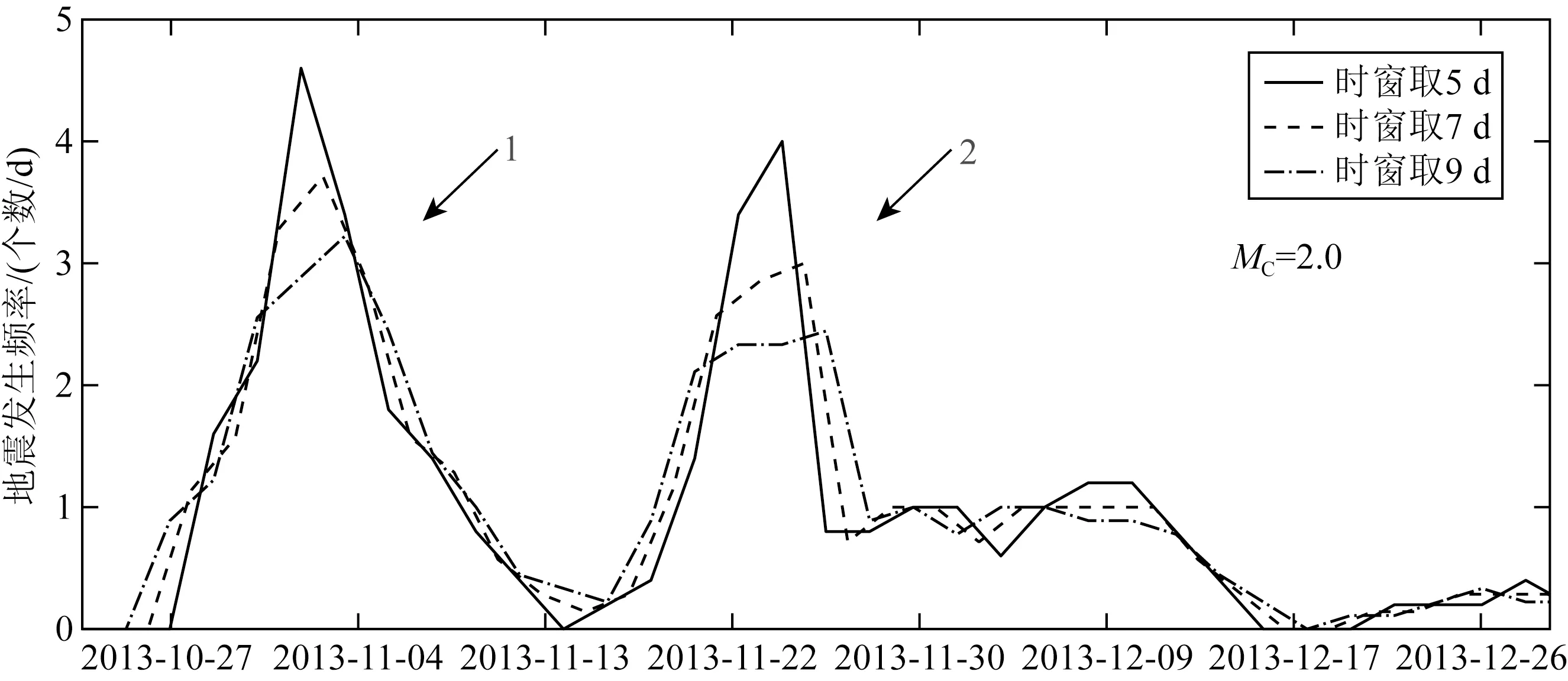
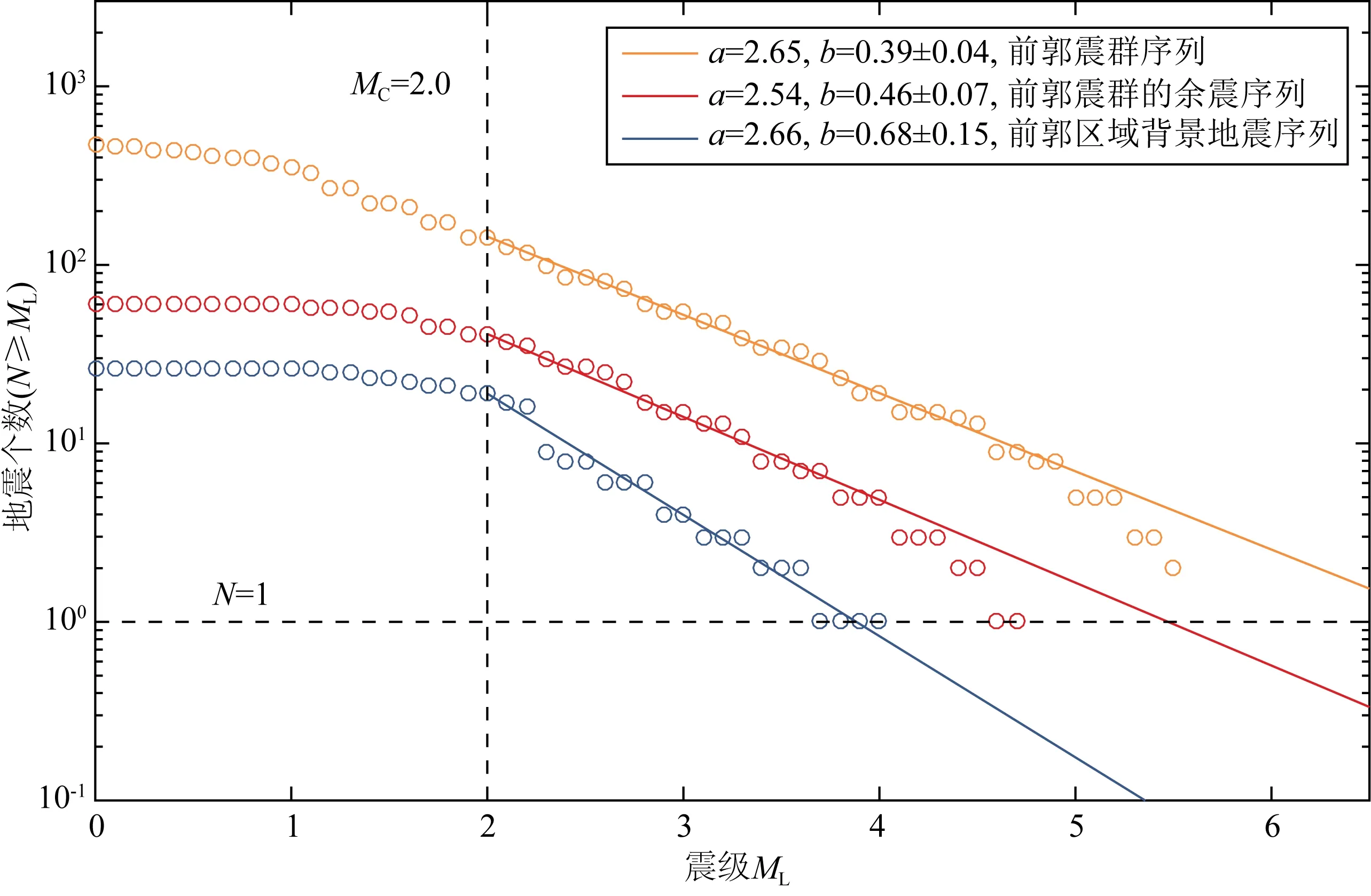
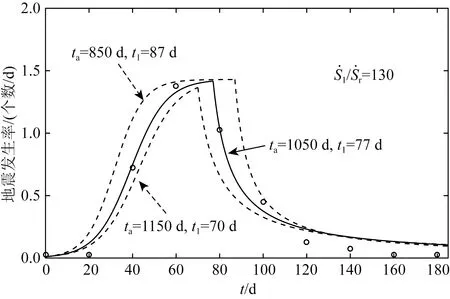
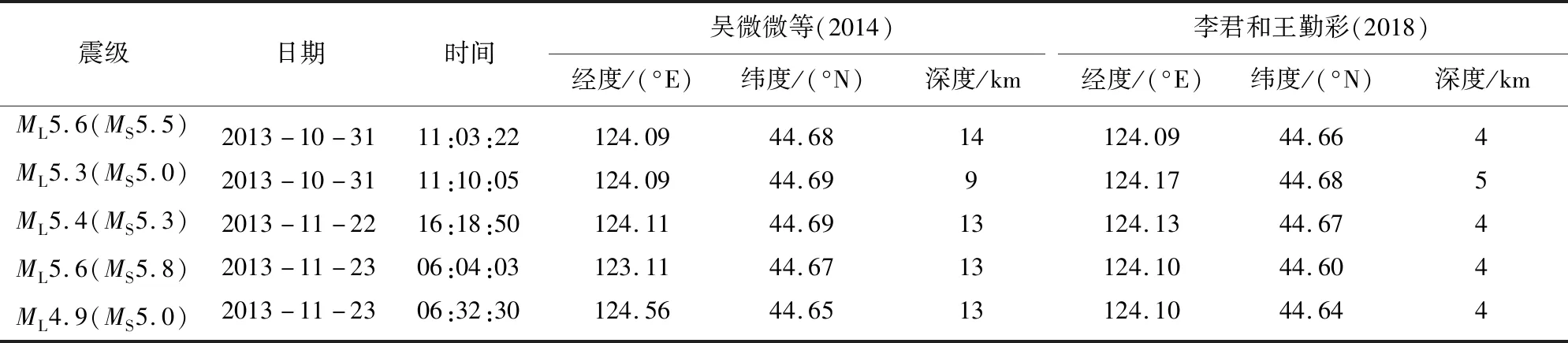
进一步,我们设定断层上的剪切应力的增加仅由远场加载函数(6a)式所主导,即剪切应力函数形式保持不变,而流体运移作用后断层上正应力的扰动量为Δσ(孔隙压力)可以是随时间变化的函数.在本文的研究中,我们仅考虑Δσ/σ0≪1情形时,Δσ的变化量对断层滑移速率的影响.孔隙压力Δσ与流体应力Δp之间的关系为Δp(t)=-B1Δσ(t),其中B1为Skempton系数(Cocco and Rice,2002).因此,当Δp>0,断层上的有效正应力则会出现明显的下降.若孔隙应力变化Δσ(t)可由扰动函数f(t)=Δσ0sin(ωt)表示,因而扰动量的变化由幅值Δτ0和角频率ω所决定,而角频率与扰动周期Tp相关(Tp=2π/ω).若流体压力变化发生在t0 (7) 当t0≤t≤t1时,且有Tp≪Δt=t1-t0及V0≈Vp l,公式(7)也可近似为: (8) 相应的滑动位移为: (9) 图1 断层相互作用概念模型图中用蓝色线围成的方块代表一个地质块体,地质块体中的黑色线段代表断层(或裂纹),数字i=1,2,3,…,N代表断层的编号,Vpl为远场对块体的加载速度,δR代表远场对块体的加载位移.Fig.1 Conceptual model of fault interactionIn the figure,the block surrounded by blue lines represents a geological block,the black line segment in the geological block represents the fault (or crack),the number i=1,2,3,…,N represents the number of the fault,Vpl represents the loading speed and δR represents the displacement. (10) (11) (12) 图2 由慢滑或非地震滑移所触发的地震发生率随时间演化特征示意图(a),(b)和(c)由本文公式(11)与(12)所给出.(a)的取值对地震发生率的影响;的取值对地震发生率的影响;(c)t1的取值对地震发生率的影响.Fig.2 Schematic diagram of the seismicity rate of earthquake swarms triggered by slow slip or aseismic slip(a),(b)and (c)are given by formulas (11)and (12)in this paper.(a)The influence of value on seismicity rate;(b)The influence of value on seismicity rate;(c)The influence of t1 value on seismicity rate. 完整的地震复发周期一般可分为4个主要阶段(Stein and Wysession,2003):①闭锁阶段;②自加速/成核阶段;③同震相;④震后松弛/滑移阶段.当震后松弛阶段结束后,断层又进入到闭锁阶段,表明新的地震循环的开始.根据Dieterich模型(1994),复发周期Tr可近似为: (13) (14) 松辽盆地位于中国的东北部,地跨黑龙江、吉林、辽宁和内蒙古,第四纪以来在盆地周边断裂控制下,总体活动趋势趋于沉降.控制松辽盆地演化发展的主要地球动力是地壳深部地幔物质的驱动和西太平洋板块向东亚大陆边缘的俯冲(高立新,2008;李恩泽等,2012).2013年前郭震群位于松辽盆地中部北东向扶余—肇东断裂和西北向查干花—道字井断裂的交汇部位附近(刘俊清等,2017),地处松辽盆地中央凹陷地区,是盆地内沉降速度最快、沉降幅度最大、坳陷最深的区域(吴微微等,2014). 本研究采用中国地震台网中心提供的2008年9月—2017年7月前郭区域(44.3°N—45°N,123.6°E—124.7°E)内的地震目录,其M-T图如图4a所示.为了便于定量研究,我们把2013年前郭震群的发生时间定为2013年10月31日—2013年12月13日,把2008年9月至2013年10月30日的地震定为背景地震,把2013年12月14日—2017年7月的地震定为前郭震群结束后的“余震”.前郭震群的空间分布和时间分布如图3和图4b所示,ML≥5.0的地震的空间位置比较集中.前郭震群序列起始于2013年10月31日11时3分的ML5.6(MS5.6)地震,结束于2013年12月13日ML1.8地震,此后研究区10日内没有探测到地震发生.前郭震群序列中地方震级ML≥5.0的地震共有4个(若采用面波震级,则MS≥5.0的地震共有5个,因为前郭震群中2013年11月23日6时32分发生的地震的震级为ML4.9或MS5.0),其中最大震级地震为2013年11月23日6时4分发生的ML5.6(MS5.8)地震.前郭区域背景地震(ML≥2.0)发生频率平均约为0.01个/d,前郭震群地震发生频率(ML≥2.0)平均约为1.56个/d,所以前郭震群地震发生频率相较于前郭区域背景地震发生频率平均提高了约156倍.图5给出了前郭震群地震发生频率随时间的变化关系,表明前郭震群序列之中有两个地震发生频率较高的时段(如图5中箭头所指),一段为2013年11月4日左右达到峰值,另一段在2013年11月23日左右达到峰值,这两个峰值点所在的时刻接近ML≥5.0地震发生的时刻. 图3 前郭震群序列空间分布图Fig.3 The spatial distribution of the Qianguo earthquake swarm 图4 不同时间尺度下的前郭区域内地震的M-T图(a)前郭区域2008年9月—2017年7月地震序列M-T图;(b)前郭震群序列M-T图.Fig.4 M-T diagram of Qianguo earthquakes with different time spans(a)M-T diagram of earthquake sequence in Qianguo area from September 2008 to July 2017;(b)M-T diagram of Qianguo earthquake swarm. 图5 前郭震群地震发生频率图由时窗推移法求得,时窗分别取5 d,7 d和9 d,每间隔2d计算一次,完备震级MC取2.0.Fig.5 Schematic of Qianguo earthquakes swarm seismicity rateThe seismicity rate is obtained by moving time window methods,the time window takes 5 days,7 days,9 days and calculated every 2 days.Minimum magnitude takes 2.0 Ross等(2020)利用美国南加州密集的台站记录到的连续地震波形数据和深度神经网络获取精确地震目录的方法,对南加州圣哈辛托(San Jacinto)断层和埃尔西诺(Elsinore)断裂之间的卡维拉谷(Cahuilla Valley)岩体附近2016—2019年发生的震群进行了分析,表明该地区地震活动的迁移是因为流体持续注入和迁移导致的,其中慢慢扩散的前锋面暗示这个震群主要是由流体运移来驱动的,而不是如典型的地震序列那样由静态或者动态应力触发来驱动.这为震群是由流体运移驱动而形成的机制提供了一个重要的依据. 由静态应力或动态应力触发的地震序列类似于由主震触发的余震序列,通常满足大森(Omori)定律和巴特(Båth)定律.前郭震群序列的地震发生率首次开始下降后,在2013年11月17日左右又开始回升(图4),因此前郭震群不满足大森定律.序列中的最大震级为MS5.8(ML5.6),第二大震级为MS5.6(ML5.6),面波震级差仅为0.2,且MS≥5.0的地震共有5个,因此前郭震群也不满足巴特定律.Dieterich(1994)地震发生率模型赋予了大森定律物理意义,描述了由应力扰动引起的地震序列的地震发生频率逐渐衰减的过程,然而同前郭震群不满足大森定律的原因相同,前郭震群也无法满足该物理模型.因此,前郭震群有可能同美国南加州卡维拉谷岩体附近的震群成因机制类似,简单的静态或动态应力触发无法解释地震的丛集现象. 古登堡-里克特定律(Gutenberg and Richter,1944)可表示为lgN(≥M)=a-bM,其中N(≥M)表示区域内震级大于等于M的地震总个数,a值代表区域内地震活动总体水平,b值的大小同区域介质特征、应力状态和不均匀性等有关,反映了区域内地震的震源特性(Rundle,1989;Marzocchi and Sandri,2003).大量资料统计的b值接近于1.0(陈培善等,2003;El-Isa and Eaton,2014),针对中国东北地区的研究表明东北地区地震的b值为0.73(吴兆营等,2005).利用古登堡-里克特定律,采用最大似然法(Marzocchi and Sandri,2003),我们分别计算了前郭区域内背景地震、前郭震群和前郭震群的余震的a和b值,得到的结果如图6所示,其中MC为完备震级.计算结果表明2008年9月—2017年7月期间前郭区域内地震的b值(<0.7)普遍小于东北地区的平均b值,前郭震群的b值小于前郭区域背景地震和前郭震群的余震的b值,说明该区域内的b值在前郭震群期间降低,而在前郭震群结束后又有上升.通过形变率与地震矩的关系,近期的研究定量地给出了b值的变化同断层上应力加载速率变化的近似关系(Hainzl et al.,2010;尚园程和史保平,2020),其关系式可表示为: 图6 不同时间尺度下的前郭区域内地震序列震级-频度(M-F)图,完备震级MC取值2.0Fig.6 The Magnitude-Frequency plot for Qianguo earthquake sequences with different time spans,Minimum magnitude takes 2.0 (15) 前人的研究表明2013年前郭震群是由流体运移的驱动而产生,这种流体可能与地幔上升所导致的深部流体向浅部的运移相关(Zhang et al.,2019),也可能与附近的油田开采相关(刘俊清等,2017).然而受限于观测条件和资料,目前无法对前郭震群序列中的全部地震进行高精度定位,从而也无法认识前郭震群发震区域内断层带的精细结构与震群的精细动态演化过程.由于该震群的震源深度平均分布在地下10 km处(吴微微等,2014),因此无法直接确定前郭震群震源区域及其附近是否存在断层的缓慢滑动现象.本文从理论上阐述了流体的运移可以触发慢滑移或非地震滑移,而慢滑移或非地震滑移可导致临近断层上剪切应力加载速率(库仑应力加载速率)上升,进而导致b值降低.因此地下流体活动所导致的慢滑或非地震滑移可能为前郭震群成因的力学机制. 图7 拟合2013年前郭震群地震发生频率(日期:2013-08-30—2014-03-03)圆圈代表实际数据,曲线代表拟合结果.实际数据由时窗推移法求得,完备震级MC取2.0,背景地震发生频率取0.011个/d.Fig.7 Fitting the seismicity rate of Qianguo earthquakes swarm in 2013 (date is 2013-08-30—2014-03-03)The circles represent the actual data,the curve represents the fitting result.The actual data is obtained by moving time window methods.Minimum magnitude takes 2.0.Background seismicity rate takes 0.011/d. 前震泛指主震发生之前的较短时间内,在主震附近发生的中小地震,加速发生的小震与古登堡-里克特定律中的b值变小是前震序列的典型特征.本文给出由流体运移而引发的慢滑移或非地震滑移所触发的震群序列的地震发生频率公式(11)在早期阶段也呈现出与前震相同的逐渐加速的特征.这是因为加速发生的前震是受主震成核所驱动的,前震断层上的剪应力加载速率在主震成核的作用下升高,与由慢滑或非地震滑移所触发的震群的力学机制相同,但前震与震群的物理过程和驱动机制是完全不同的.前震序列会伴随着破坏力较大的主震,而震群序列中大多是中小地震,若能在地震序列的初始阶段判断这段序列是前震还是震群将会十分有利于地震灾害的预测及防范,而我们对震群的研究可表明在现有的台网精度下利用地震是否加速发生的现象来分辨前震序列和受慢滑移或流体运移驱动的震群序列是不可行的.Gulia和Wiemer(2019)的研究表明,矩震级MW>6.0地震的余震的b值一般比该区域内背景地震的b值大20%左右,而若MW>6.0地震发生后所伴随的“余震序列”的b值相对背景地震的b值不变或变小,则该序列可能为后续更大震级地震的前震序列,并依此提出了FTLS(Foreshock Traffic Light System)以用于评估地震风险.流体运移所引发的慢滑或非地震滑移可以导致断层上剪应力加载速率的升高进而触发震群,断层上剪应力加载速率升高同样会导致震群序列的b值降低,因此,b值降低不是前震序列所独有的特征,利用b值变小判别前震序列是不完全准确的.FTLS成立的条件是矩震级MW>6.0,而前郭震群并不满足这一条件,未来还需针对含有MW>6.0地震的震群序列进行研究. 前郭震群序列中MS≥5.0的地震共有5个,均呈逆冲断层兼少量走滑性质(吴微微等,2014),且震源机制解整体上具有良好的一致性(李君和王勤彩,2018).针对这5个地震,表1给出了吴微微等(2014)及李君和王勤彩(2018)给出的精确定位结果,表明这5个地震的空间位置十分相近.本文的拟合结果表明前郭震群期间2级以上地震的平均复发周期降为原来的1/130,所以区域内的一些断层在前郭震群期间重复失稳多次的可能性是存在的.再考虑到这5个地震具有一定的相似性,因此本文认为目前不能排除前郭震群序列中MS≥5.0的5个地震是一个或几个(小于等于4)5级断层的重复失稳的可能性.但由于数据精度的限制,目前只能从理论上提出这种可能性,其验证方式与方法仍是一个尚待解决的问题. 表1 前郭震群序列中MS≥5.0地震的精确定位结果(吴微微等,2014;李君和王勤彩,2018)Table 1 Accurate location results of MS≥5.0 earthquakes in Qianguo earthquakes swarm (Wu et al.,2014;Li and Wang,2018)
1.5 断层相互作用模型和慢滑移/蠕变滑移触发震群的机制
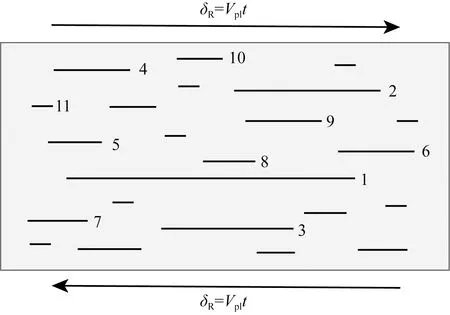
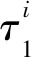
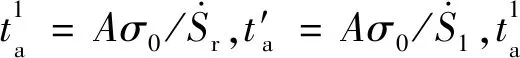
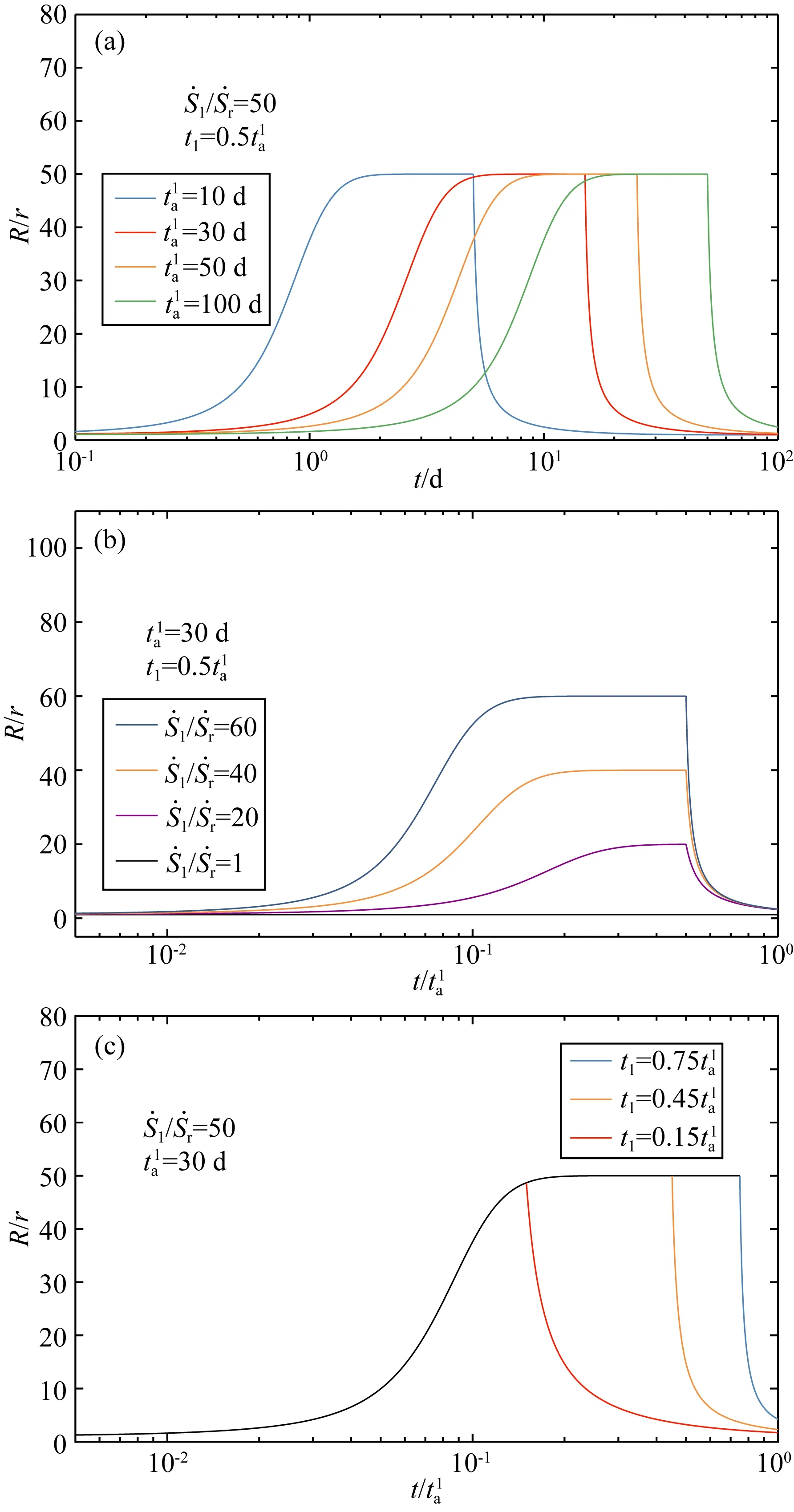
1.6 基于地震复发周期的近似解分析慢滑或非地震滑移对震群的影响
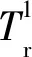
2 2013年前郭震群序列分析
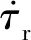
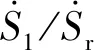
3 讨论
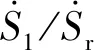
4 结论