单活塞线性斯特林制冷机半正定减振系统研究
孔德锐,夏 明,唐天敏,毕 翔
〈制冷技术〉
单活塞线性斯特林制冷机半正定减振系统研究
孔德锐,夏 明,唐天敏,毕 翔
(昆明物理研究所,云南 昆明 650223)
当前,对于吸振器和单活塞线性斯特林制冷机振动系统的研究,几乎都是在已知制冷机进行某种固定安装方式的正定模型上进行的。而这种正定方法由于缺乏对制冷机和吸振器系统固有频率的分析,当改变系统的安装方式后,可能会产生共振并减小吸振器的减振效果。基于此,本文将对制冷机和吸振器振动系统在未进行任何安装时的半正定模型进行理论分析,并通过悬挂测试法对制冷机适配吸振器前后进行振动实验。由此得到了系统在半正定模型下的理论固有频率值为78.6Hz。而通过实验可发现,受吸振器实际加工和装配的影响,系统的固有频率随吸其刚度的增大而增大,其增大的范围在78.1~80.8Hz之间。
单活塞线性斯特林制冷机;吸振器固有频率;半正定模型
0 引言
随着红外探测器朝着高温区发展,所需的制冷温度降低,增加了对制冷机小尺寸(size)、轻质量(weight)和低功耗(power)的SWaP要求,这使得单活塞线性斯特林制冷机的应用逐步广泛[1-2]。单活塞线性斯特林制冷机相较于旋转集成式而言具有可靠性高和降温时间短等特点,而较于双活塞对置式又具有质量轻、尺寸小和安装灵活性高等优点[3-4]。
尽管这种制冷机具有出众的性能优势,但因为压缩机独特的单活塞结构,使其运行时会在轴向上产生较大的惯性力,并对外输出振动,这也成为进一步提高单活塞线性斯特林制冷机竞争力的一大技术难点。基于此,目前许多著名的制冷机研发机构常通过适配吸振器对其振动进行消减和抑制,例如RICOR公司的K527,AIM公司的SX030和SUNPOWER公司的GT型制冷机等,图1所示为K527和GT型制冷机适配吸振器的实物图[5-8]。
这些研发机构在进行吸振器的相关理论分析和设计中,都是在已知制冷机固定安装方式下进行的,其振动模型如图2所示[9-11]。
在图2所示的几个振动模型中,质量为2,刚度和阻尼分别为2和2的吸振器与质量为1的制冷机相联,然后通过刚度1,阻尼1的柔性弹簧安装于固定支座。尽管这种正定振动模型结合傅里叶变换后可以很方便地分析并计算得到吸振器的相关参数,但当需要对制冷机采用悬挂法测试其相关性能或改变制冷机固定安装方式后,整个系统的固有频率也会随之改变,这极有可能使制冷机和吸振器系统在工作频率处发生共振。因此,需要对制冷机在未进行任何固定安装前,分析系统的固有频率和相关振动特性。
本文将在这种正定振动模型的基础上,同时引入无约束的半正定振动模型参与分析。
1 正定与半正定振动系统
1.1 正定振动系统
在图3所示的制冷机与吸振器正定振动模型中,质量、刚度和阻尼系数分别2、2和2的吸振器与质量为1的制冷机相联,然后通过刚度1,阻尼1的隔振弹簧安装于固定支座,为制冷机在时域输出的振动诱导力。
从上述模型可以得到以下双自由度振动微分方程:
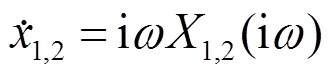
式中:i为虚数单位;为制冷机工作频率。
为方便后续分析,将傅里叶变化后的参数带入微分方程组(1),并将解析结果进行无量纲化后,可得到制冷机在适配吸振器后的振动表达式:

图1 K527(a)和GT(b)型制冷机适配吸振器实物图
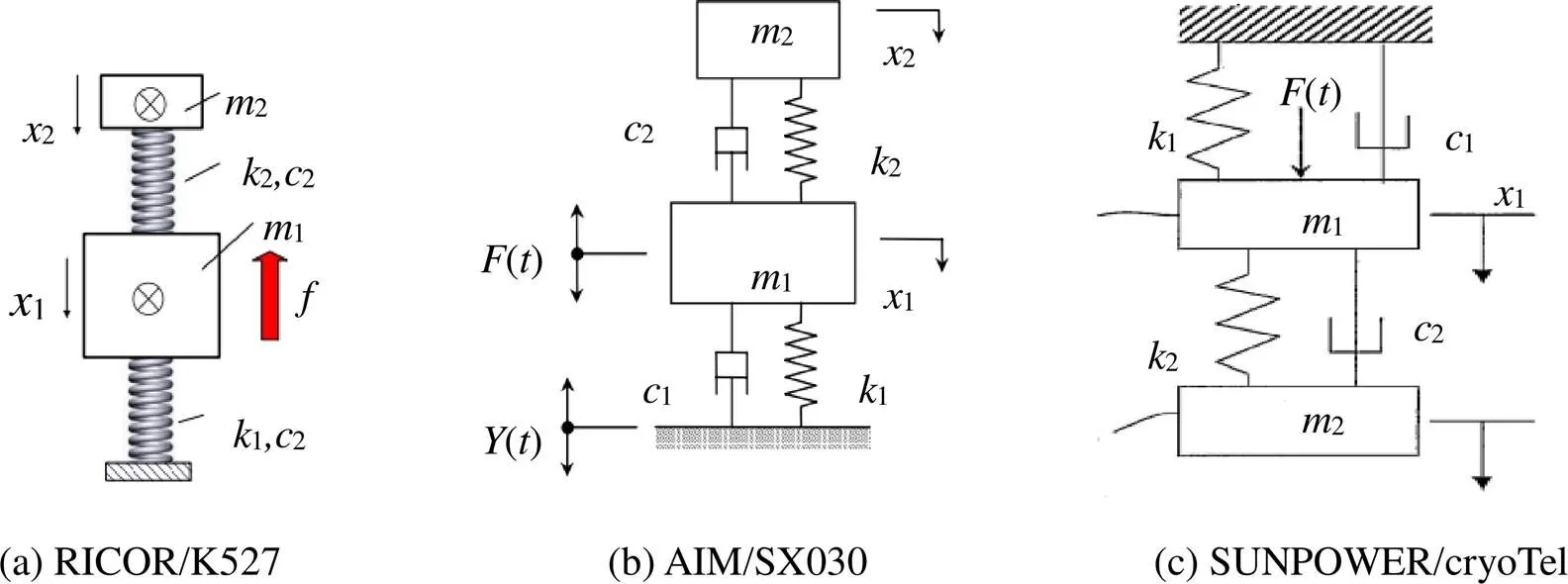
图2 吸振器与制冷机正定振动模型
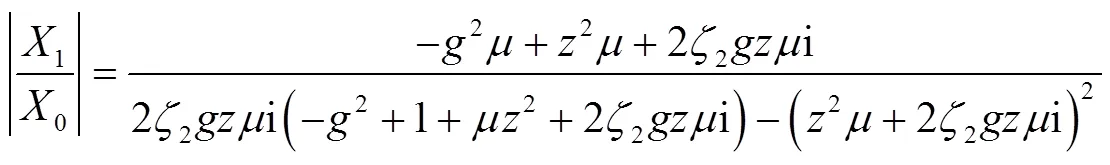
式中:=2/1;=2/1=(2/2)1/2/(1/1)1/2;=/1;2=2/[2(22)1/2];0=(i)/1;
从式(2)可以分析得知,制冷机相关参数和系统安装方式已知的前提下,制冷机的振动输出仅和质量比及吸振器阻尼比2有关。此外,还可以清楚地发现,当吸振器2等于制冷机工作频率时,制冷机输出的振动最小,且在振动最小值左右会出现两个共振点。图4分别为制冷机振动幅频特性与质量比和吸振器阻尼比2的关系曲线。
从图4(a)中可以看到,在制冷机工作频率75Hz处其振动随质量比的增大而减小。由于本文所参与分析的制冷机质量为1=300g,1=66620N/m为了同时兼顾系统轻质量的要求,所以可选择=1/10,即选择吸振器质量为30g。而根据在工作频率处制冷机振动最小的条件2=,可计算得到所需吸振器刚度为6662N/m。
1.2 半正定振动系统
通过前文对系统正定模型的分析,得到了吸振器重要的设计参数,而为了分析制冷机与吸振器系统的固有频率,在此将引入半正定振动模型。如图5所示,吸振器质量、刚度和阻尼系数分别为2、2、2的吸振器安装于质量为1的制冷机。
对于该系统而言,半正定模型与正定模型的区别在于是否对制冷机进行固定约束。而在对此模型求解固有频率时,根据公式(3)可知,仅与系统的刚度和质量有关,与吸振器阻尼和振动诱导力无关。

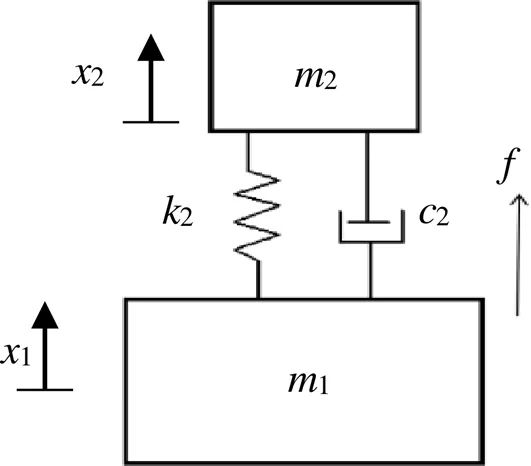
图5 制冷机与吸振器半正定振动模型
由此可建立式(4)的振动矩阵方程:

从该矩阵方程可以知道,因为半正定模型的刚度矩阵[]为奇异矩阵,所以在这种情况下,系统仅有一个不为零的固有圆频率sys,经计算可得:
sys2=1.12(5)
式中:2=(2/2)1/2,由此可解得系统得固有频率sys=78.6Hz。
由式(6)则可计算得到系统在此固有频率下的振型。
[-sys2]=0 (6)
由此解得制冷机和吸振器的振动幅值比为1/2=1/10,如图6所示。通过对该振型的计算,可对制冷机和吸振器系统进行悬挂测试,分析在不同工作频率下两者振动的位移幅度值比,当比值为1/10时,根据共振原理,此时对应的工作频率即为系统固有频率。
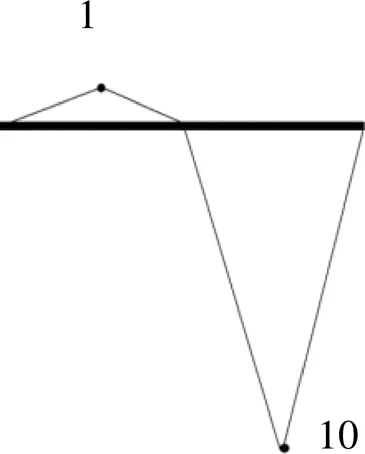
图6 半正定系统振型
2 半正定振动系统仿真分析
2.1 固有频率分析
通过上述的分析与计算,可得到系统的理论固有频率,但因为在实际过程中或多或少会受到吸振器阻尼的影响,因此还需进一步进行相关分析和验证。
式(7)为图5对应的双自由度振动微分方程:
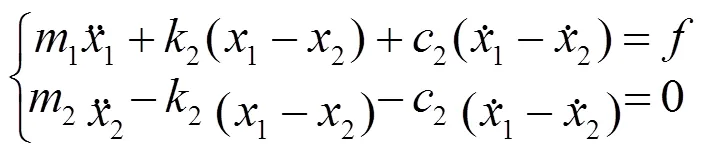
同样,对相关参数经傅里叶变换后,可得到如式(8)所示当制冷机在半正定情况下时,适配吸振器后的振动表达式:
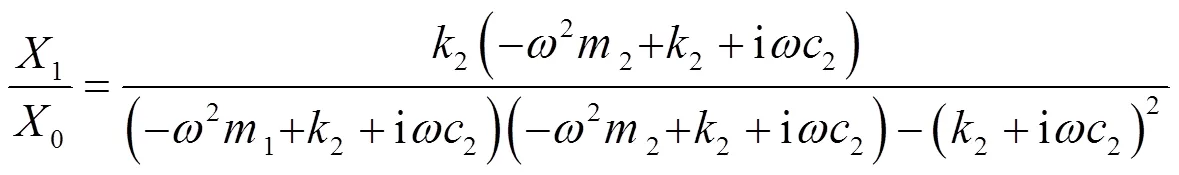
通过该式可以得到图7所示当吸振器质量2=30g时的制冷机振动幅频特性曲线。
从式(4)和仿真曲线可以看到,在这种半正定情况下,当吸振器2等于制冷机工作频率且在75Hz频率处工作时,其振动仍然为最小值。而从图中可以看到,无论吸振器阻尼如何变化,当制冷机工作频率为78.9Hz时均会出现一个共振点,此共振频率即为系统在半正定情况下的固有频率。该结果与1.2节的解析解较为接近,从而验证了系统固有频率与吸振器阻尼无关。
2.2 半正定系统MATLAB/Simulink仿真
前文通过计算和仿真的方法得到了半正定系统的固有频率,但因为在实际应用中无法达到这种理想的无固定约束状态,所以可借助Simulink的仿真方法得到一个理论值。图8是通过式(7)建立的Simulink仿真框图。

图7 半正定系统下制冷机振动幅频曲线
仿真结果见图9所示。
从仿真结果来看,在此半正定系统下,制冷机适配吸振器后,其输出的振动加速度峰值为6.56m/s2左右,因为输出的理论振动波形为正弦波,所以其有效值约为4.64m/s2。
3 实验分析
为了使制冷机在实验中接近半正定无约束状态,本文采用悬挂法测试,实验平台如图10(b)所示。
由前文理论分析可知,制冷机与吸振器半正定系统固有频率可通过测试不同工作频率下两者的振动幅值来确定,当其幅值比为1/10时,对应的工作频率即为系统的固有频率,测试结果如图11(a)所示。从图中可看到,在制冷机10W工作功率范围内,满足两者振幅比为1/10的频率值在78.1~80.8Hz之间,且呈增长趋势。
虽然从前文理论分析可知,系统的固有频率是系统的固有属性,它与吸振器阻尼及振动诱导力无关。但出现这种现象的原因在于实际的吸振器刚度2是非线性的,即当吸振器在不同幅值下做往复运动时,其刚度不是一个定值。因此,随着输入功率的增加,增大了驱动吸振器运行的振动诱导力,从而加大了吸振器振幅2,其刚度2也随之增大,如图11(b)所示。由此可知,系统的固有频率也相应地有所增大。但在制冷机可运行的功率下,其系统实变化的固有频率与理论值误差较小。
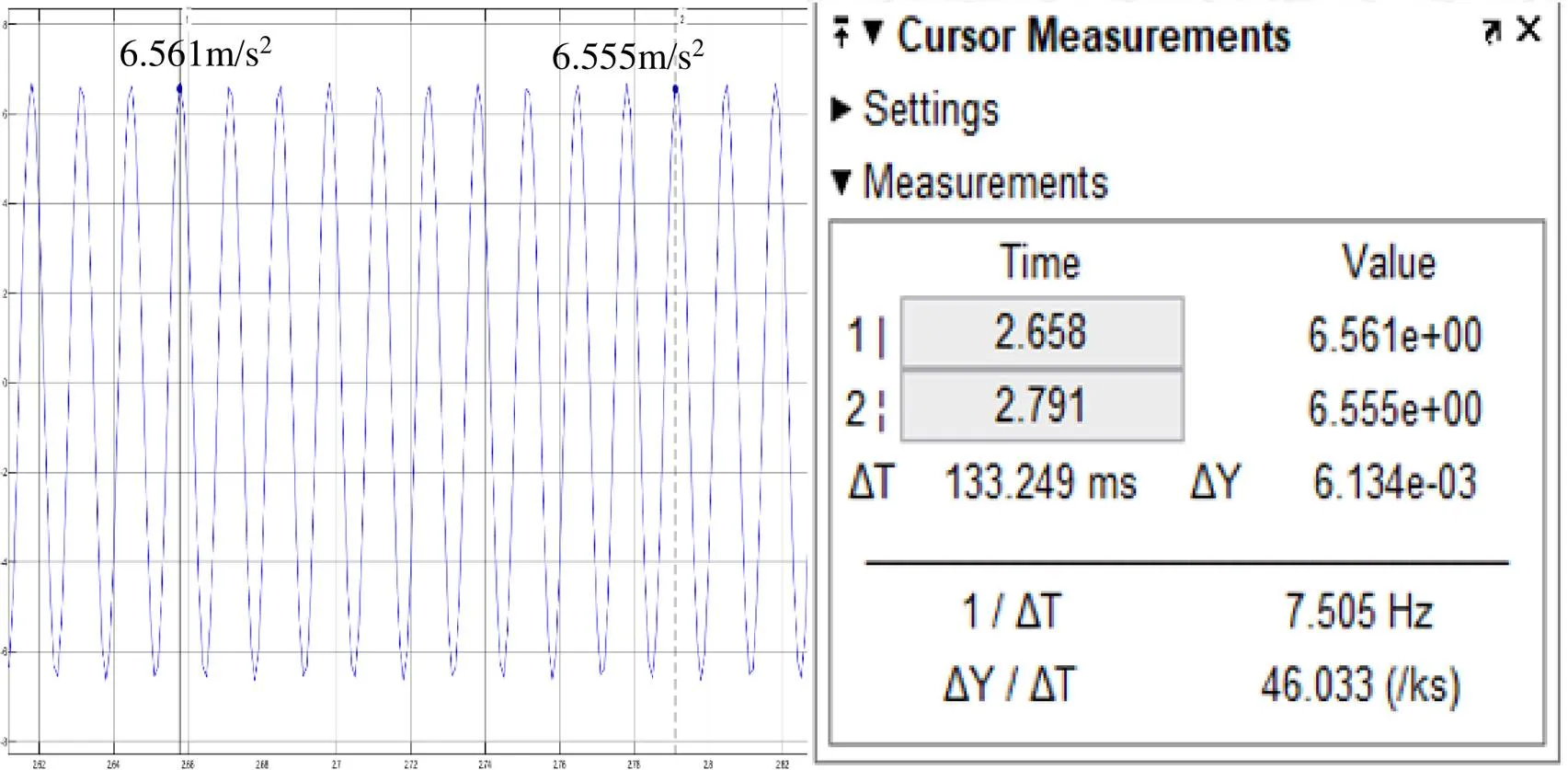
图9 半正定系统Simulink仿真结果

图10 制冷机与吸振器(a),测试实验台(b)
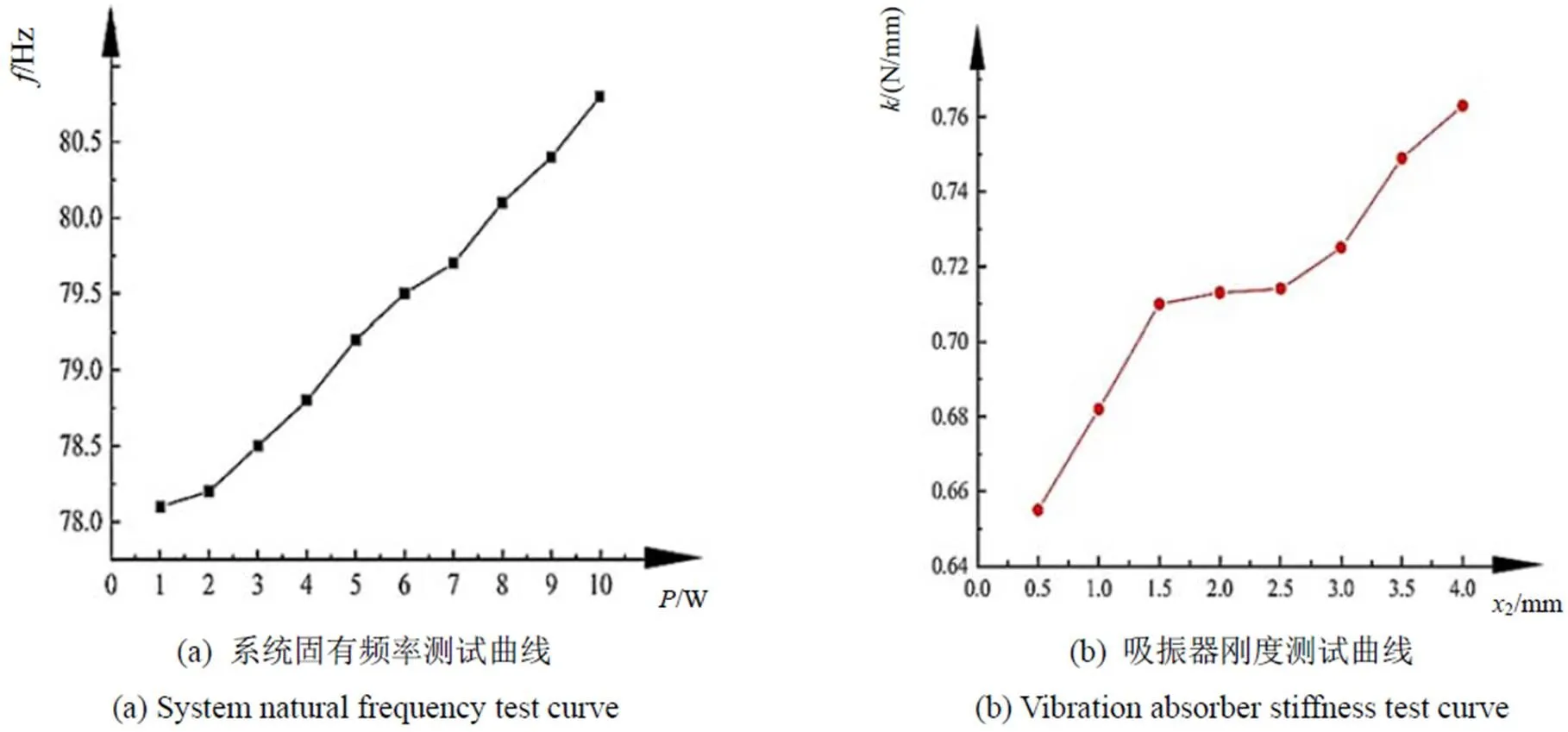
图11 系统固有频率和吸振器刚度测试曲线
而在对制冷机常用的6W输入功率下进行适配吸振器后,经悬挂测试得到的减振前后振动加速度值,见图12所示。从实验结果可以看到,制冷机在半正定系统下,经吸振器减振后,可以从减振前的有效值42.474m/s2降低至减振后的3.047m/s2,这与图9所示的仿真值存在一个可接受的误差。造成这种误差的原因在于,采用悬挂法测试时,在制冷机轴向上细绳仍会提供一个很小的约束刚度。而仿真则采用的是理想半正定模型,约束刚度为零,从而导致了实际值和仿真值存在一定的误差。
4 结论
单活塞线性斯特林制冷机在适配吸振器后,其振动可得到有效的抑制。在进行研究的过程中,本文引入了半正定模型参与分析,并得到以下几个结论。
①在半正定情况下,制冷机适配吸振器后,要使其在工作频率75Hz处的振动最小,仍要求吸振器固有频率2等于制冷机工作频率。而且在半正定情况下,系统仅会在制冷机振动最小值的右侧出现一个共振点。
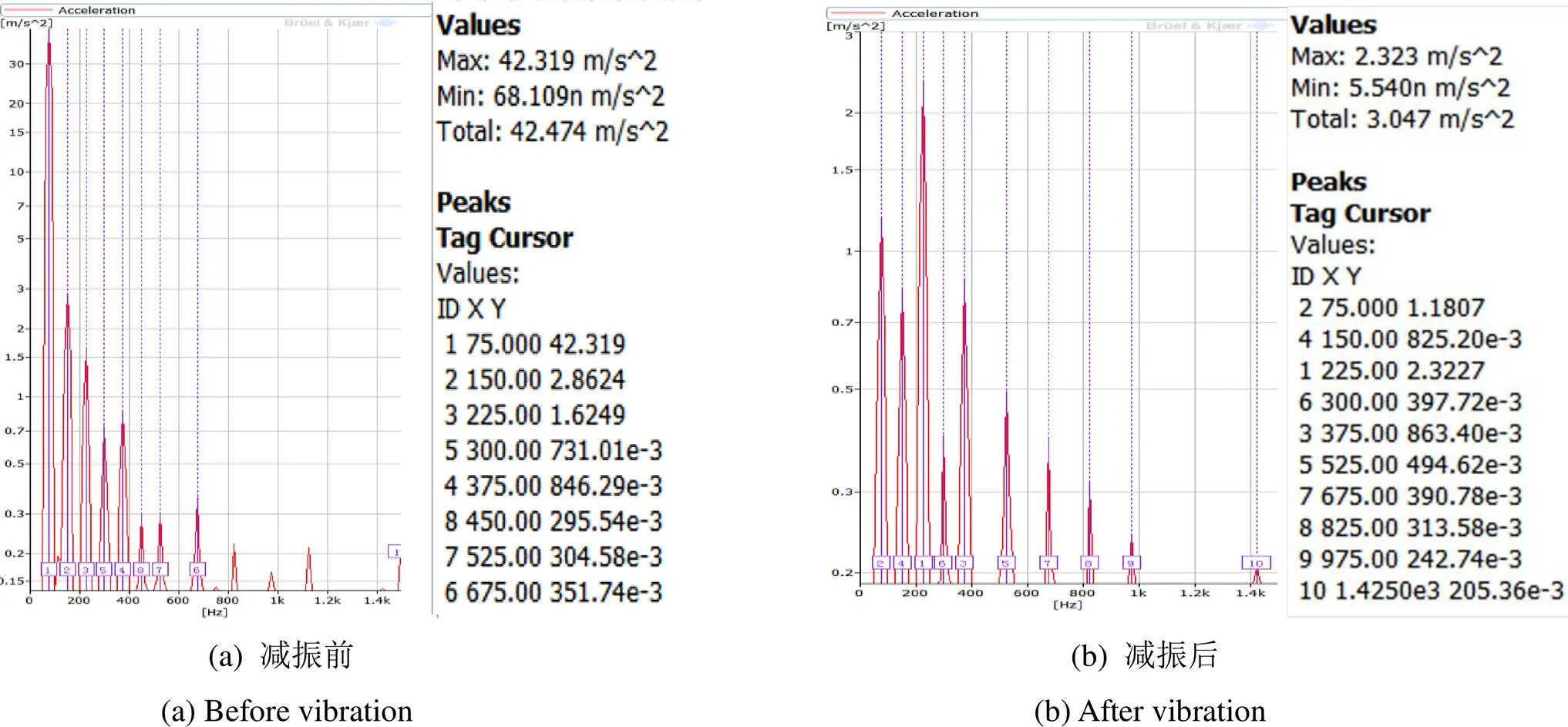
图12 制冷机减振前后振动频谱图
②本文通过相关理论得到的半正定系统固有频率解析解与仿真值较为接近,而通过实验得到的系统固有频率则与吸振器的刚度呈正相关增长,这主要是由于吸振器的非线性刚度造成的。但在制冷机可运行的输入功率范围内,其实际值范围78.1~80.8Hz与理论值78.6Hz的误差较小。
③通过悬挂测试制冷机在6W输入功率的情况下,其减振前后的加速度有效值分别为42.474m/s2和3.047m/s2,其中由于理论模型和实际测试条件存在一定的差异,导致减振后的数值与理论仿真值4.64 m/s2存在一定的误差。
[1] Epstein R I, Andresen B F, Hehlen M P, et al. Development and optimization progress with RICOR cryocoolers for HOT IR detectors[C]//, 2016, 9821: 98210N.
[2] Mai M, Ruehlich I, Rosenhagen C, et al. Development of the miniature flexure bearing cryocooler SF070[C]//, Kluwer Academic/Plenum Publishers, 2009: 133-138.
[3] Rühlich I, Mai M, Withopf A, et al. AIM cryocooler developments for HOT detectors[C]//, 2014, 9070: 90702P.
[4] Rühlich I, Mai M, Rosenhagen C, et al. Compact high efficiency linear cryocooler in single piston moving magnet design for HOT detectors[C]//,,, 2012, 8353: 83531T.
[5] 孔德锐, 夏明, 李海英, 等. 单活塞线性压缩机用动力吸振器理论分析与Matlab仿真[J]. 红外技术, 2021, 43(10): 1014-1021.
KONG Derui, XIA Ming, LI Haiying, et al. Theoretical analysis and Matlab simulation of dynamic vibration absorber for single-piston linear compressor[J]., 2021, 43(10): 1014-1021.
[6] Veprik A, Vilenchik H, Riabzev S, et al. Novel microminiature linear split Stirling cryogenic cooler for portable infrared imagers[C]//, 2007, 6542: 65422F.
[7] Veprik A, Zechtzer S, Pundak N. Compact linear split Stirling cryogenic cooler for high temperature infrared imagers[C]//, 2008, 16: 121-132.
[8] Rosenhagen C, Rühlich I. Compensating oscillation device: US20160153512A1[P]. European Patent WO, 2014: 358-361.
[9] Sunpower. Cryocoolers Overview[EB/OL][2020-12-28]. https://www. sunpowerinc.com/products/stirling-cryocoolers.
[10] Amiram Katz, Victor Segal, Avishai Filis, et al. RICOR's cryocoolers development and optimization for HOT IR detectors[C]//, 2014, 9070: 90702N.
[11] Avishai Filis, Zvi Bar Haim, Tomer Havatzelet, et al. RICOR's rotary cryocoolers development and optimization for HOT IR detectors [C]//, 2012, 8353: 83531U.
Research on Positive Semi-Definite Vibration Damping System of Single-Piston Linear Stirling Cryocooler
KONG Derui,XIA Ming,TANG Tianmin,BI Xiang
(,650223,)
At present, research on the vibration system of the vibration absorber and the single-piston linear Stirling cryocooler is almost entirely carried out on the positive definite model of a certain fixed installation method for the known cryocooler system. Owing to the lack of analysis of the system’s natural frequency using this method, resonance may occur, and the damping effect of the vibration absorber may be reduced when the installation method is changed. Therefore, this study conducts a theoretical analysis of the positive semi-definite model of the cryocooler and the vibration system of the vibration absorber without any installation and performs vibration experiments before and after the cryocooler is fitted with the vibration absorber through the suspension test method. The theoretical natural frequency value of the system under the positive semi-definite model is 78.6 Hz. Through experiments, it can be found that, due to the actual processing and assembly of the vibration absorber, the natural frequency of the system changes with the vibration absorber’s stiffness within the range of 78.1 to 80.8 Hz.
single-piston linear Stirling cryocooler, vibration absorber, natural frequency, positive semi-definite model
TB652
A
1001-8891(2022)01-0096-07
2021-09-06;
2021-10-07.
孔德锐(1993-),男,云南昭通人,硕士研究生,研究方向:小型低温制冷机。E-mail:1024197919@qq.com。
夏明(1977-),男,研究员,主要从事小型低温制冷机研究。E-mail:15969586435@163.com。

