基于力位混合控制的机器人充电枪装配寻孔算法

(浙江工业大学 信息工程学院，浙江 杭州 310023)

随着电动汽车的普及，电动汽车充电的问题也随之而来。目前，电动汽车充电主要靠驾驶员来完成，需要花费大量的人力、物力。实现电动汽车自动化充电将是大势所趋。现阶段实现电动汽车自动化充电的技术难点是充电枪的装配。随着机器人技术的发展，使用机器人代替人类完成充电枪的装配不再遥不可及。搭载传感器的机器人完成充电枪装配面临如下挑战：区别于常见的圆形轴孔装配，充电枪装配是一个类圆形孔轴装配；充电枪头的半径为25.50 mm，充电枪座半径为25.75 mm，两者配合公差仅为0.25 mm；初始定位不准确，很容易导致装配失败。为了解决上述问题，笔者提出了利用机器人搭载双目视觉与力传感器进行充电枪装配的寻孔控制方法，先通过双目视觉获取充电枪座的位姿，再通过改进的梯形线速度规划阿基米德螺线寻孔算法配合速度环的力位混合控制，实现充电枪柔顺快速寻孔作业。

目前，机器人轴孔装配分为被动柔顺控制[1]和主动柔顺控制。被动柔顺控制凭借一些辅助的柔顺机构，使其在与环境接触时能够对外部作用力产生自然顺从来完成装配；主动柔顺控制利用各类传感器的反馈信息，采用一定的策略控制接触力从而完成装配。主动柔顺控制中有一小部分是先通过视觉反馈提取图像边界，再对整个装配过程进行控制[2-4]，绝大部分还是通过力信息的反馈来实现接触力的控制，从而完成对整个装配过程的控制。国外Damme等[5-7]通过基于伺服电机的电流信息估计获得机器人末端的接触力从而完成装配，不过无力传感器对接触力的估计存在较大的误差，不适用于高精度的场合；Shirinzadeh等[8]通过在机器人手臂上安装力传感器对圆柱形桩孔进行综合研究。Newman等[9-12]提出了力-力矩图，包括每个点的力信息，通过六维力传感器反馈的接触力定位寻孔方向；Kamal等[13]将轴孔装配搜索转化为最优化搜索问题去解决。国内芦俊等[14]提出了基于自适应阻抗控制[15]的轴孔装配方法；张庆伟等[16-17]进行了基于速度环的力位混合控制的仿真；吴炳龙等[18]在此基础上提出了力位混合控制和螺旋搜索策略，从而实现工业机器人大臂减速机的装配，但是阿基米德螺线搜索需要遍历所有工作范围，从而导致寻孔效率低的问题。此外，阿基米德螺旋搜索会因为轴孔异面产生较大的位置偏差而导致装配失败。笔者在该方法的基础上进行改进，提供了一种类圆形孔的解决方案，提高了寻孔算法的效率和稳定性。

针对电动汽车充电枪装配问题，提出一种基于速度环的力位混合控制快速寻孔算法。在位置空间，考虑到双目视觉的初始定位不能满足装配要求，设计了一种基于梯形线速度规划的阿基米德螺线轨迹规划，在此基础上对类圆形轴孔装配中充电枪头与充电枪座的两点接触进行静力分析，引入向心力引导使得螺线旋转中心向装配中心移动，改进了阿基米德螺线轨迹规划。实验结果验证了笔者算法的优势和应用价值：针对充电枪装配作业，笔者算法能在保证寻孔成功率的前提下，极大地提升寻孔效率，有效地降低寻孔过程中接触力的波动。

1 问题定义

电动汽车充电枪装配系统示意图如图1所示，系统主要包括双目视觉系统、机器人、六维力传感器、电动汽车充电枪头和电动汽车充电枪座。在系统中建立了机器人基坐标系{B}、传感器坐标系{S}、充电枪头坐标系{T}和充电枪座坐标系{G}。电动汽车充电枪装配主要分为3个阶段：充电枪座定位阶段、寻孔阶段和孔内装配阶段。充电枪座定位阶段：双目视觉系统根据图像使用中值滤波、边缘特征的提取以及基于边缘特征的模板匹配算法等得到充电枪插座的六维位姿信息并发送给机器人[19]。寻孔阶段：系统通过引入寻孔算法来完成双目视觉系统初始定位误差的补偿。孔内装配阶段：寻孔成功后，使用导纳控制实现柔顺装配，同时根据力信息和位置信息，判断是否完全装配。

图1 电动汽车充电枪装配系统示意图Fig.1 Schematic diagram of electric vehicle charging gun assembly system

在充电枪装配过程中，因为充电枪插座表面结构复杂，内部为金属材质的多轴孔，图像背景特征难提取，作业现场光照变化大、反射不均，所以会对最后得到的充电枪座六维位姿造成较大的误差，从而导致直接进行充电枪装配的成功率变低。充电枪插头和充电枪座近距离接触后，双目视觉系统处于视觉盲区，不能再次定位充电枪座的位姿，需要通过其他方法完成对初试定位误差的补偿，因此引入充电枪寻孔算法。由于导致装配失败的主要原因是位置误差，因此笔者使用阿基米德螺线轨迹搜索方法的同时结合向心力引导来实现位置最大误差范围内的快速稳定寻孔。在下文中将阿基米德螺线简称为螺线，将阿基米德螺线轨迹搜索的同时结合向心力引导的寻孔算法简称为改进的螺线寻孔算法。

2 充电枪寻孔的力位混合控制

充电枪寻孔阶段的控制器采用了基于速度环的力位混合控制，控制系统结构图如图2所示。控制器负责的力位混合控制由两部分组成：机器人在{G}坐标系Z方向的力控制和XY方向的位置控制。此外控制器还向机器人发送{B}坐标系的速度指令，从而完成对机器人的控制[20]。

图2 力位混合控制系统结构图Fig.2 Structure of force position hybrid control system

在六自由度的力位混合控制中，不同的自由度使用了对应自由度的信息分量。当选择矩阵对应自由度的元素为1时，表示这个自由度的信息分量被使用，当选择矩阵对应自由度的元素为0时，表示这个自由度的信息分量没有被使用。XY方向与Z方向的选择矩阵分别为

SXY=diag(1,1,0,0,0,0)

(1)

SZ=diag(0,0,1,0,0,0)

(2)

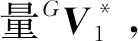
(3)

(4)

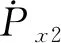
(5)

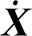
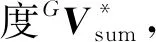
(6)

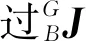
3 阿基米德螺线轨迹规划

阿基米德螺线轨迹如图3所示，螺线轨迹规划属于力位混合控制中的位置控制，通过扫描搜索实现双目视觉初始定位最大误差范围内的寻孔操作。为了实现对螺线线速度的速度规划，在螺线表达式中引入时间函数f(t)，则螺线极坐标表达式为

ρ=rθ

(7)

r(t)=Δrf(t)

(8)

θ(t)=ωf(t)

(9)

式中：ρ为极径；r为搜索半径；θ为搜索角度；ω为固定角速度；Δr为半径增量。Δr取充电枪头和充电枪座配合公差的2倍，若半径增量过大，会出现扫描搜索盲点，导致寻孔失败。若半径增量过小，则会出现搜索区域重合，增加搜索时间。XY平面的螺线寻孔轨迹如图3所示。

图3 阿基米德螺线轨迹图Fig.3 Archimedes spiral trajectory

螺线线速度幅值的表达式为

(10)

随着时间的增加，(ωf(t))2≫1，则线速度可以简化为

v(t)≈Δrωf(t)f′(t)

(11)

虽然此时不是真正意义上的螺线，但是对于本寻孔方法的影响完全可以忽略。

线速度规划前的螺线时间函数表达式为f(t)=t，线速度规划前的螺线方程为

ρ=r(t)θ(t)=Δrtωt=Δrωt2

(12)

线速度规划前的螺线线速度表达式为

v(t)≈Δrωt

(13)

线速度规划前的螺线的线速度会随着时间的增加而增加，{G}坐标系Z方向误差也会越来越大，导致寻孔失败。为了保证运动的稳定性，需要将线速度设定成一个恒定值，此外启动时加速度过大，容易产生抖动，故把速度分为2 段。在t0到t1时刻设定加速度为a+的匀加速运动，在t1到t2时刻设定最大线速度为Vmax的匀速运动，即

(14)

将式(14)代入式(11)可以求解出线速度规划后的时间函数，其中k为速度比例常数，即

(15)

(16)

对应XY平面线速度规划的螺线笛卡尔坐标系表达式为

Px1=r(t)cos(ωt)=Δrf(t)cos(ωf(t))

(17)

Py1=r(t)sin(ωt)=Δrf(t)sin(ωf(t))

(18)

4 向心力轨迹规划

向心力轨迹规划用于改进螺线寻孔算法。通过对静态接触力进行分析，确定充电枪头中心和充电枪座中心之间的相对关系。充电枪座是一个类圆形孔，在不接触竖梁的情况下可以按圆形孔分析，根据接触状态可以分为4 种情况：平面接触、两点接触、三点接触和面接触，其分类图如图4所示。

图4 接触状态分类图Fig.4 Contact state classification diagram

在不同的接触状态下，充电枪头和充电枪座的静力分析都不相同，笔者只针对两点接触进行静力分析。一方面是因为两点接触出现的概率最大；另一方面是在充电枪装配前，可以通过倾斜策略在{G}坐标系Ry方向转动偏转角β，将接触状态都转化为两点接触[21]，同时又能避免竖梁的接触，如图5所示。双目视觉系统初始定位的充电枪座的位置可能在充电枪左边或者右边，通过倾斜策略调整为虚线表示的位置，随后沿着虚线的中心轴线即{G}坐标系Z方向向前运动，直到接触到充电枪座，从而变成两点接触状态。此外，在充电枪寻孔过程中也不会出现由两点接触转变为三点接触的情况，造成三点接触的主要原因有充电枪和充电枪座之间配合公差较大和充电枪座初试定位姿态误差较大。因为本方法适用的控制系统已经通过双目视觉系统初始定位将姿态误差控制在较小的范围之内，而且实际充电枪轴孔配合公差仅为0.25 mm，所以在实际的寻孔过程中不会出现三点接触情况。

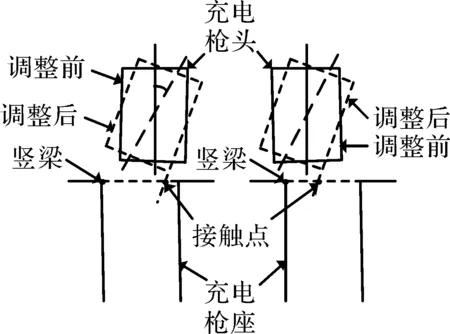
图5 倾斜策略后接触状态分类Fig.5 Contact state classification after tilt strategy

对于两点接触状态，在基于静态接触力的分析下，可以得到充电枪头中心和充电枪座中心之间的相对关系，其示意图如图6所示。由于充电枪对充电枪座保持一个恒定的接触力，所以充电枪座会分别在接触点A和接触点B对充电枪生产反作用力Fa和Fb，其合力方向就是指向装配方向的向心力Fsum，而Fx和Fy则是向心力在{T}坐标系上的受力分解。向心力Fsum的方向α可根据静态接触力分析结果计算得到，即

α=atan2(Fx,Fy)

(19)

将螺线轨迹规划的最大线速度施加到向心力的方向，则{G}坐标系XY方向的速度分量分别为

(20)

(21)

图6 两点接触状态静力分析示意图Fig.6 Static analysis diagram of two point contact state

5 实 验

为了验证笔者充电枪装配寻孔算法，采用大族六轴协作机器人Elfin10、ATI六维力传感器作为开发平台，将带有Codesys的ARM工控机、六维力传感器和大族机器人组建成局域网，利用带有Codesys的ARM工控机通过TCP通讯发送机器人运动指令，实现机器人的运动，实验平台实物图如图7所示。实验分为3部分：第1部分为梯形速度规划前后螺线寻孔算法的对比，以验证速度规划的必要性；第2部分为改进的螺线寻孔算法寻孔实验，分析寻孔过程中的各个方向的实际运动轨迹和接触力曲线情况；第3部分为3种寻孔算法对比实验，以验证笔者算法的优势。

图7 电动汽车充电枪装配系统Fig.7 Electric vehicle charging gun assembly system

5.1 线速度规划对比实验

为了验证螺线寻孔轨迹速度规划的必要性，进行了线速度规划前后的对比实验。设计系统在{G}坐标系Z方向保持-10 N的期望接触力，XY平面上分别进行线速度规划前后螺线寻孔算法的对比，实验结果如图8所示。速度规划前螺线寻孔算法的实际接触力成正弦变化，且随着时间的增加，幅值也在不断增加；速度规划后的螺线寻孔算法的实际接触力基本稳定在-10 N左右。

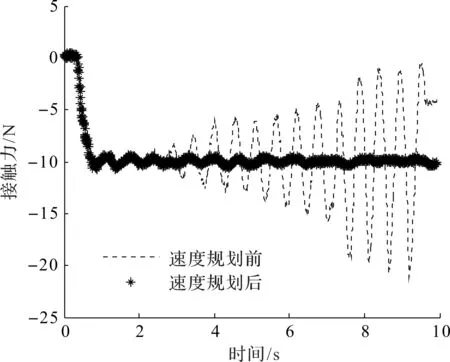
图8 速度规划前后螺线寻孔算法对比图Fig.8 Comparison of spiral hole finding algorithm before and after speed planning

因为充电枪头与充电插座异面，所以距离中心点越远，Z方向存在的位置偏差越大。速度规划前，随着时间的增加，螺线的半径也越来越大，线速度也随着无限增加，然后导致Z方向的位置偏差越来越大，实际控制器的响应不能满足需求，从而出现Z方向接触力的波动，且随着时间的增加而增加，最后甚至会出现充电枪头和充电枪座悬空的情况，即Z方向接触力为0 N，出现系统错误判断工作状态导致装配失败的情况。速度规划后，随着时间的增加，螺线的半径也越来越大，但线速度成梯形变化，最后稳定在设计的最大线速度。因为Z方向的位置偏差在控制器能调节的范围内，所以实际接触力可以保持一个稳定的值。

5.2 改进的螺线寻孔算法寻孔实验

为了方便观察改进螺线寻孔算法的轨迹，将系统初始定位误差设定为较大的值。设定系统在{G}坐标系Z方向保持恒定的接触力-10 N，Ry方向添加β=5°的偏转角，起点的坐标为[618.10 55.48 809.70 -87.84 3.42 -102.10]，终点的坐标为[615.40 56.04 812.70 -87.84 3.42 -102.10]。改进的螺线寻孔算法寻孔轨迹如图9所示。

图9 寻孔轨迹图Fig.9 Hole-finding trace

由图9可知：寻孔轨迹呈螺旋状，且螺线的中心也向充电枪座方向移动。改进的螺线寻孔算法从0.7 s开始寻孔操作，经过5.1 s完成整个寻孔过程。寻孔过程中力、力矩的变化如图10所示。在整个寻孔过程中，除了Z方向外其他力、力矩变化不大，只有在快接近充电枪座时，充电枪与充电枪座内壁接触，产生一定的接触力，Fx在-2.5 N附近，Fy在5.0 N附近，只有Fz一直处于力控制状态，所以重点分析Fz的数据。在0～0.7 s时，系统处于准备状态，充电枪开始靠近充电枪座，所以Fz均为0 N。在0.7～5.8 s时，系统处于寻孔状态，充电枪和充电枪座开始接触，Fz开始变化。螺线轨迹规划虽然减少了Fz的力波动，但是引入向心力之后会存在一个指向装配方向的速度，从而导致Fz额外产生5 N左右的波动。实际寻孔过程中，Fz在-5～-15 N之间变化。在5.4～5.8 s时，Fz从10 N开始逐渐变小，最后变成0 N，此时表示寻孔已经成功。

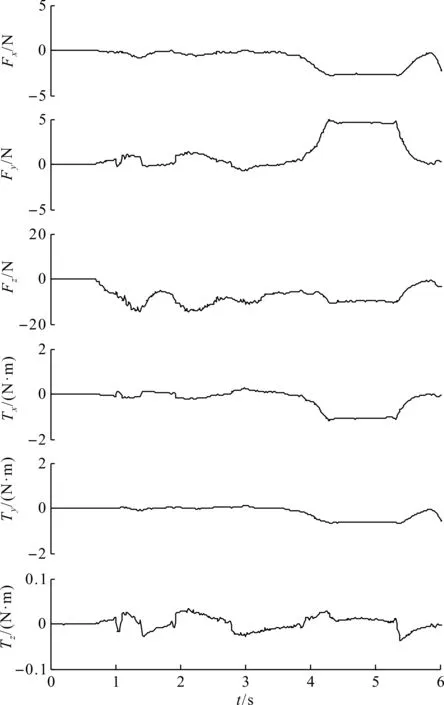
图10 寻孔实验过程的力、力矩传感器数据Fig.10 Force, torque sensor data during holefinding experiment

5.3 寻孔算法对比实验

为了验证本系统寻孔算法的优势，进行3 种寻孔算法的对比实验。设计系统在{G}坐标系Z方向保持恒定的接触力-10 N，Ry方向添加β=5°的偏转角，在XY平面坐标正负误差为5 mm区域内，对每1 mm2都分别进行螺线寻孔算法、改进的螺线寻孔算法和向心力引导寻孔算法的对比实验，且每种算法均进行了121 次实验，实验结果如图11～13所示。

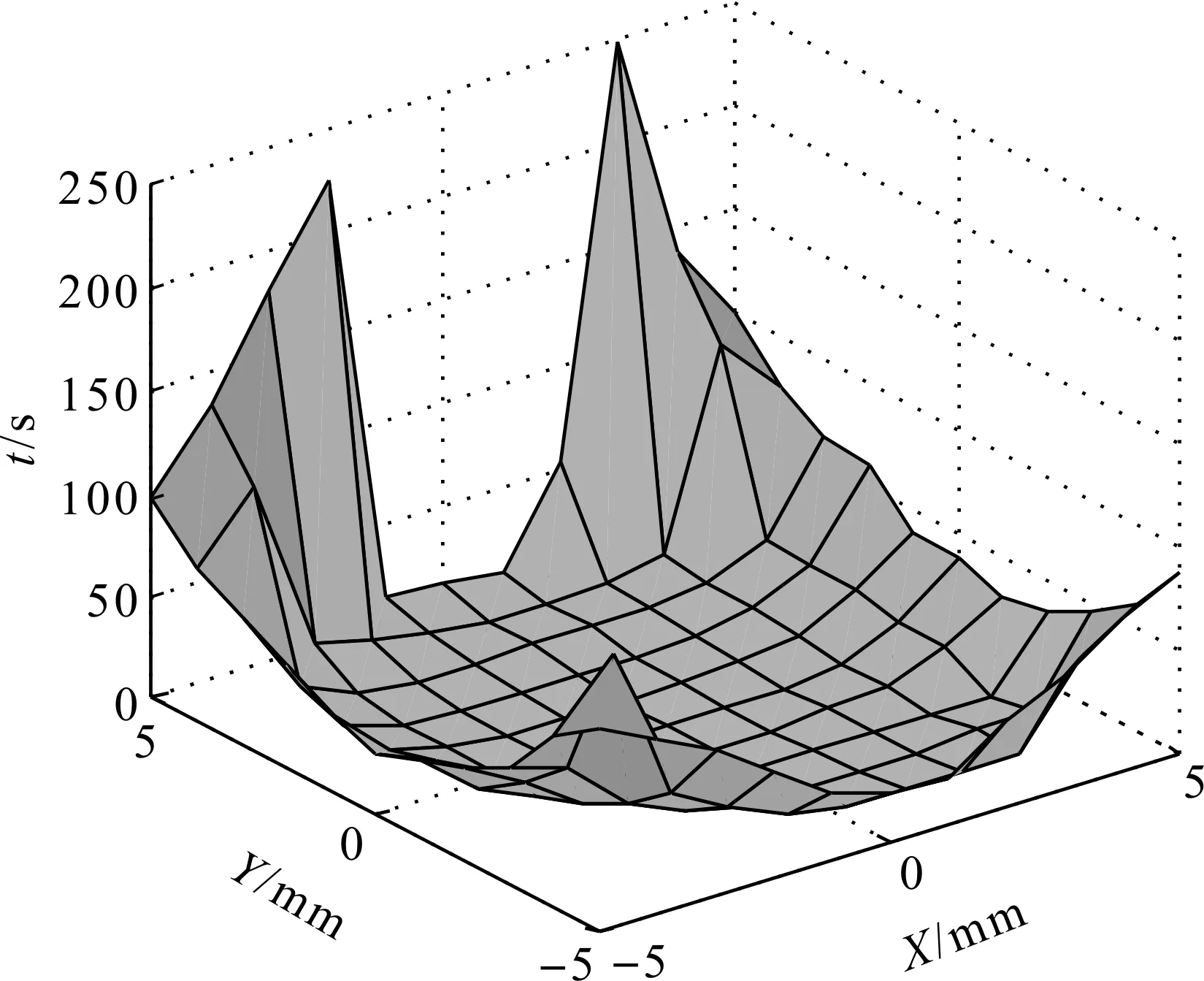
图11 螺线寻孔算法耗时图Fig.11 Time-consuming graph of spiral hole finding algorithm

图12 向心力引导寻孔算法耗时图Fig.12 Time-consuming graph of centripetal force guided hole finding algorithm

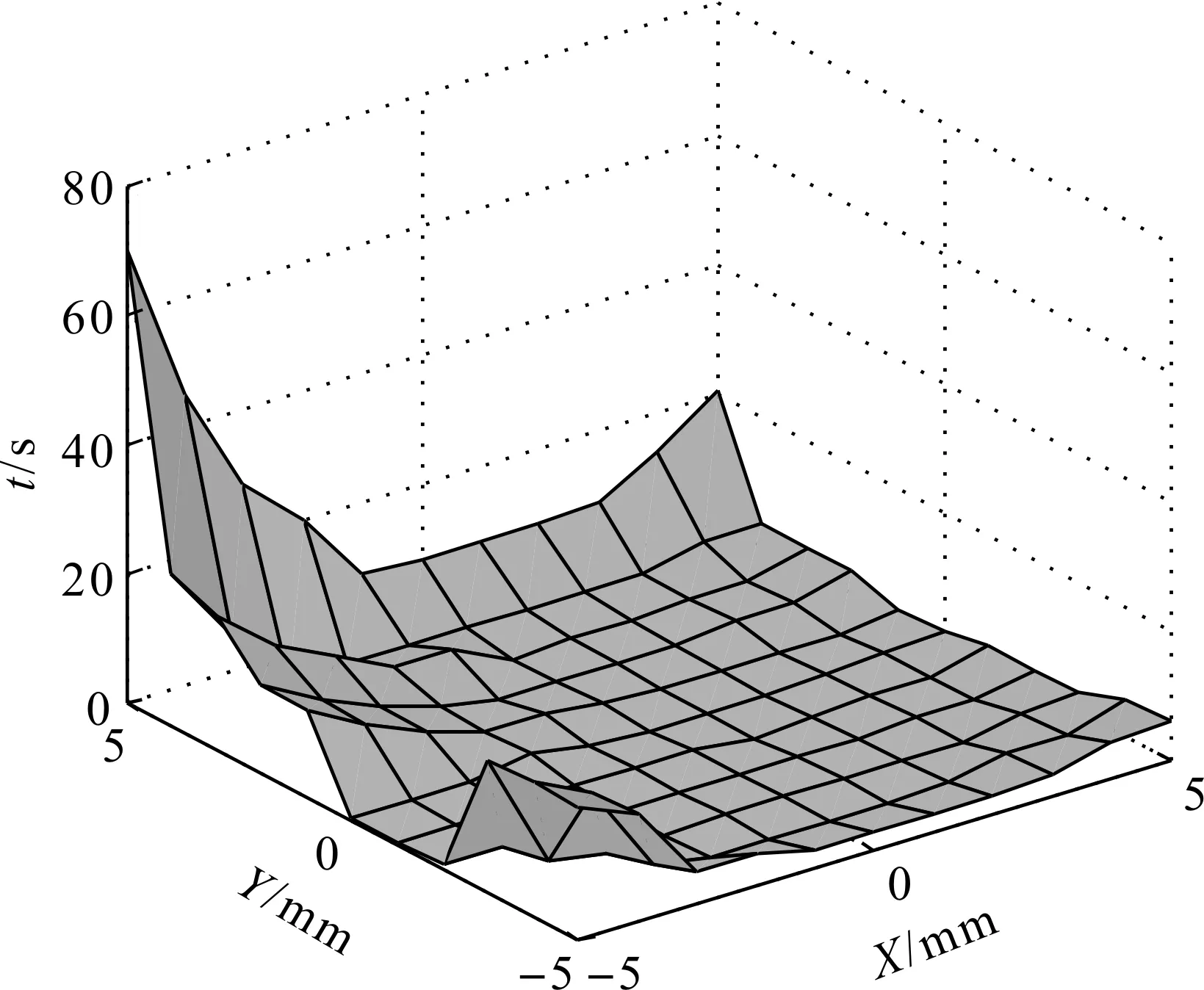
图13 改进的螺线寻孔算法耗时图 Fig.13 Time-consuming graph of improved spiral hole finding algorithm

线速度规划螺线寻孔算法寻孔耗时如图11所示，平均用时34.96 s，寻孔时间随着离中心点的路径增大而增长。寻孔最长时间出现在最大误差附近(249.53 s)，寻孔最短时间出现在离中心点误差为1 mm半径的圆内，此时可以直接完成装配。此算法寻孔成功率为100%。向心力引导寻孔算法耗时如图12所示，平均用时2.50 s，寻孔时间随着离中心点的路径增大而增长。寻孔最长时间出现在最大误差附近(9.04 s)，寻孔最短时间出现在离中心点误差为1 mm半径的圆内，可以直接完成装配。在X方向误差为-5 mm时，充电枪头会与充电枪座在竖梁接触，直接导致向心力方向不指向充电枪的装配方向，从而导致寻孔失败。此算法寻孔成功率为97.52%。改进的螺线寻孔算法耗时如图13所示，平均用时5.16 s，寻孔时间随着离中心点的路径增大而增长。寻孔最长时间出现在最大误差附近(70.38 s)，在X方向误差为-5 mm时，充电枪头会与充电枪座在竖梁接触，直接导致向心力方向不指向充电枪的装配方向，螺线部分的速度可以继续使得充电枪头运动，充电枪离开竖梁，系统能继续完成寻孔。寻孔最短时间出现在离中心点误差为 1 mm 半径的圆内，可以直接完成装配。此算法寻孔成功率为100%。

3 种寻孔算法的对比如表1所示。螺线寻孔算法虽然成功率高，但是寻孔效率低，需要花费大量的时间。向心力引导寻孔算法具有寻孔效率高、耗时短的优点，但是在接触竖梁的情况下会出现寻孔失败的情况。改进的螺线寻孔算法具有两者的优点，其寻孔时间为螺线寻孔算法耗时的1/7，其寻孔成功率为100%。在实际生活中，考虑到系统的工作效率和工作稳定性，采用改进的螺线寻孔算法。

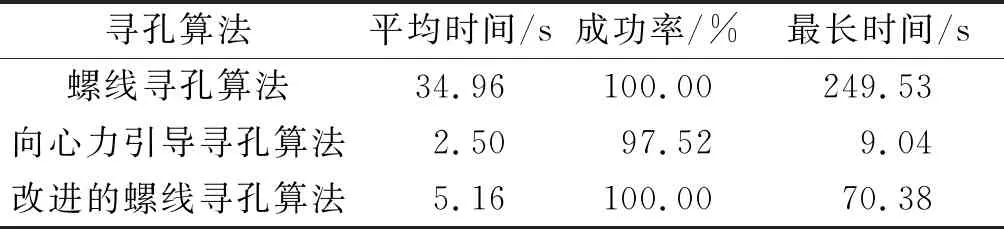
表1 寻孔算法对比Table 1 Comparison of hole finding algorithms

6 结 论

以电动汽车充电枪装配作业为背景，提出了一种基于力觉和视觉引导的电动汽车充电枪寻孔算法。首先，针对双目视觉初始定位不能满足直接装配要求的问题，设计了一种螺线轨迹规划，并对其进行梯形线速度规划，避免了充电枪头和充电枪座两者悬空导致装配失败；然后，为了提升寻孔效率，通过倾斜策略将接触状态转化成两点接触并对其进行静力分析，得到了指向装配方向的向心力并将其转换成附加速度，从而改进了寻孔算法；最后，验证了笔者提出的寻孔算法的可行性。笔者算法在保证成功率的前提下大大提高了寻孔效率，后续将进一步研究孔内装配阶段参数和控制方法的优化。