双层波纹夹芯结构的弯曲性能

吴龙飞,刘 杨,朱晓磊,陆晓峰

(南京工业大学 机械与动力工程学院,江苏 南京 211800)

复合材料夹芯结构相较其他轻质多孔材料具有结构简单、加工制造方便等优点,在满足结构强度要求的同时可大大减小结构质量,因此被广泛应用于航空航天、船舶及交通运输等领域[1-4]。近年来,对于复合材料夹芯结构的力学性能,国内外学者进行了大量的研究。高峰等[5]制备了点阵式和格构式两类界面增强型复合材料夹芯板,通过试验和有限元分析发现泡沫芯材经树脂柱点阵增强后,其剪切强度得到了提高,而剪切模量的增强效果不明显;格构式界面增强技术可有效提升泡沫芯材的剪切强度和剪切模量。史慧媛等[6]对轻木复合材料夹芯结构进行四点弯疲劳试验,建立了该类型结构的非线性疲劳损伤模型。Yan等[7]研究了三点弯载荷作用下的泡沫填充金属波纹夹芯结构的力学性能,发现填充泡沫块能显著提高整体结构的抗弯性能。Rejab等[8]研究了3种不同材质的波纹夹芯板在压缩情况下的失效模式,以及胞元数量和壁厚对面板整体变形和局部塌陷行为的影响。欧阳懿桢等[9]采用理论与试验结合的方式研究了不同设计参数下复合材料夹芯板的侧压性能,对极限承载力及失效模式进行了分析。蔡婧[10]针对蜂窝夹芯和泡沫夹芯进行了层间剪切对比试验,对其应力分布、失效模式进行了总结分析。Atashipour等[11]研究并讨论了剪切变形对复合材料夹芯板横向剪切刚度的影响。Zhang等[12]针对复合材料波纹夹芯结构,考虑了纤维类型、波纹角度、芯材厚度以及黏接长度对弯曲性能的影响。洪俊青等[13]采用高阶剪切理论和有限元方法对3种复合材料夹芯结构进行了单向受弯应力分析,研究结果对复合材料夹芯板的分析和设计提供了指导。俸翔等[14]同样采用高阶剪切理论对复合材料夹芯板的屈曲强度分散性进行了分析。陈向前等[15]制备了一种双向纤维腹板增强复合材料夹芯板,通过试验研究发现双向纤维腹板增强复合材料夹芯板可显著提高试件承载能力,还能有效减缓面层的剥离破坏。Vitale等[16]研究了复合材料夹芯板在三点弯试验下的力学性能和失效模式。Ghazali等[17]研究了四点弯试验下含孔及修复后夹芯板的极限强度,并通过有限元分析预测了修复后夹芯板的强度。Safari等[18]研究了添加泡沫对复合材料夹芯板力学性能的影响。韩丽婷等[19]对复合材料型材连接的夹芯结构进行了受弯试验研究, 确定了复合材料夹芯结构胶结节点的合理搭接长度。

综上所述,针对复合材料夹芯结构的研究主要集中在泡沫夹芯,而单层波纹以及三维点阵中未见双层波纹夹芯结构。考虑到单层波纹属于单向增强结构，同时三维点阵夹芯结构的面芯力学性能较弱,本文设计并制备了一种复合材料双层波纹夹芯结构,并对其进行三点弯试验,探究夹芯结构在弯曲载荷下的极限承载力及失效模式,同时建立与之对应的有限元模型,从而进一步讨论波纹方向和角度以及单向增强波纹位于受压侧或受拉侧对结构弯曲性能的影响,为双层波纹夹芯结构的设计与应用提供指导。

1 试验

1.1 试样制备

本文试样均采用真空辅助成型(VARI)工艺进行制备,复合材料夹芯结构采用高强玻璃纤维平纹布,单层布的厚度为0.2 mm,泡沫芯子采用聚氯乙烯(PVC)泡沫,树脂采用环氧乙烯基树脂。上、下面板厚度均为2 mm,中间面板厚度为0.8 mm,波纹筋的厚度为0.8 mm,结构尺寸如图1所示。将切割好的纤维布和泡沫按顺序排好(图2(a))，利用真空辅助成型工艺进行制备(如图2(b))，加工好的试样如图2(c)所示,试样尺寸为270 mm×90 mm×37 mm。

1.2 三点弯试验

双层波纹夹芯结构弯曲试验依据《夹层结构弯曲性能试验方法》(GB/T 1456—2005)[20]进行,跨距为200 mm。在压头和试样之间放置橡胶垫块,利用MTS万能试验机进行位移加载,加载速度为2 mm/min；利用电子千分表采集跨中挠度,采集频率为2 Hz,试样装夹后如图3所示。

图1 结构尺寸(mm)Fig.1 Geometrical parameters(mm)

图2 试样加工过程Fig.2 Sample processing

图3 三点弯试验Fig.3 Three-point bending test

1.3 试验结果

试验测得的3个试样的载荷-位移曲线如图4所示。在试验过程中3个试样呈现相似的失效过程,即面板的局部压溃,结果如图5所示。由图4可以看出:3条曲线趋势一致,曲线大致可以分为3个阶段,在加载的初始阶段,载荷呈线性增长,夹芯结构发生弹性变形(图6(a));随着位移的继续加载,面板和泡沫变形量逐渐增大,在达到第一个拐点后,载荷-位移曲线迅速下降,原因是上面板纤维发生断裂(图6(b));随着位移的继续加载,曲线缓慢上升,直到中间面板逐渐发生开裂(图6(c)),之后曲线不再上升。从试验的载荷-位移曲线获得3个试样的极限承载力分别为6.44、6.27、6.81 kN,计算得到的平均极限承载力为6.51 kN。试验过程中的失效模式主要是上面板和中间面板先后发生开裂,最终导致结构失去承载能力。相较发生同样失效模式的单层波纹结构,双层夹芯结构在上面板发生损伤后,中间面板的存在会使得双层结构能继续承载。

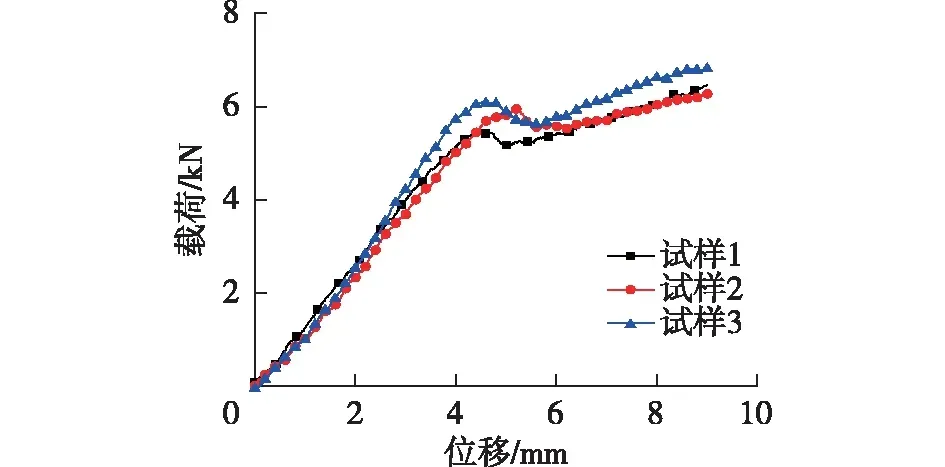
图4 3个试件载荷-位移曲线Fig.4 Load-displacement curves of three specimens

双层波纹结构的弯曲刚度(D)可由式(1)计算得到。

(1)

式中:ΔP为试验初始段载荷增量,l为试样的跨距,S为ΔP对应的试样跨中挠度增量。

试样达到极限承载力时的面板应力(σ)可表示为

(2)

式中:b为试样宽度，H为试样厚度，tf为面板厚度。

计算得到的弯曲刚度和面板应力如表1所示。

图5 试验后的双层波纹夹芯结构试样Fig.5 Double-layer corrugated sandwich structure samples after test

图6 双层波纹夹芯结构试验过程Fig.6 Test process of double-layer corrugated sandwich structures

表1 双层波纹夹芯结构的弯曲性能

2 数值分析

2.1 有限元模型

双层波纹夹芯结构采用三维实体建模,模型如图7所示。上、下压头设置为刚体,压头与双层波纹夹芯结构的接触设为“刚性”接触。对上面板以及上层波纹进行网格细化处理,网格类型为C3D8R,全模型共110 898个网格单元。下压头的边界条件设为完全固支,上压头设置位移加载。复合材料的损伤起始采用3D-Hashin准则[21],损伤扩展采用Chang-Chang准则[22]。纤维增强树脂基复合材料中纤维材料参数如表2所示;由于泡沫芯子可压缩,故采用crushable foam模型,泡沫材料参数如表3所示。

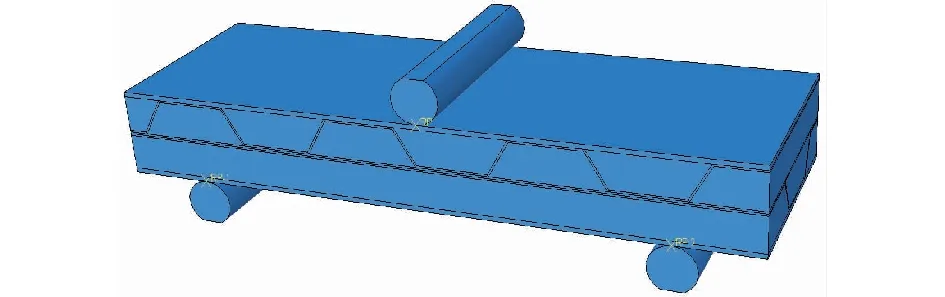
图7 有限元模型Fig.7 Finite element model

表2 纤维材料属性

表2中:E11、E22、E33分别为材料1、2、3方向的弹性模量;μ12、μ13、μ23分别为材料12、13、23方向的泊松比;G12、G13、G23分别为材料12、13、23方向的剪切模量;XT、YT、ZT分别为材料1、2、3方向的拉伸强度;XC、YC、ZC分别为材料1、2、3方向的压缩强度;S12、S13、S23分别为材料12、13、23方向的剪切强度。

表3 泡沫材料属性

2.2 模拟与试验结果对比

图8为有限元计算与试验的载荷-位移对比曲线。由图8可知:在加载的初始阶段,载荷随着位移的增大而线性增大；当曲线达到拐点后,载荷随着位移的增大而下降,这是因为双层波纹结构的上面板发生纤维压缩损伤(图9(a)),这与试验中出现的上面板发生断裂相对应(图6(b));随着位移的继续加载,载荷出现轻微上升,但变动幅度不大,此时,中间面板发生纤维压缩损伤(图9(b))。有限元计算得到的极限承载力为5.85 kN,弯曲刚度为5.62×108N·mm2,与试验结果相比，误差分别为10.14%和9.98%。三点弯试验与有限元计算模型在极限承载力和失效模式上都对应良好,这表明有限元模型是可靠的。此外,由于有限元模型未在上压头和试样间设置橡胶块,这使得有限元计算曲线在初始段的斜率大于试验段的斜率,而橡胶垫的存在可以延缓试样局部损伤,使得载荷-位移曲线的拐点更晚到来。

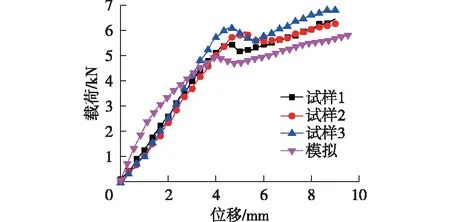
图8 模拟与试验的载荷-位移曲线Fig.8 Load-displacement curves of simulated and tested specimens

图9 模拟的失效模式Fig.9 Simulated failure modes

试验中的加载点位于夹芯结构上层波纹的波谷处,现对加载点位于波峰处的情况进行模拟计算,结果如图10所示。由图10可知:除上面板发生纤维压缩失效外,压头下方在受压变形后发生树脂基体的压缩失效,两次失效分别发生在位移加载到5.8和7.9 mm时。通过计算得到结构的极限承载力为6.79 kN,相较加载点位于波谷处时的结果提高了16.1%,这主要是由于波纹芯子参与了结构的承载,对结构有加强作用。计算得到的结构弯曲刚度为5.77×108N·mm2,与加载点位于波谷处时的结果相差并不明显,这是因为两个模型的厚度和波纹排布的方式相同,加载点的位置不同主要影响压头处局部失效的载荷,而整个结构的抗弯截面模量变化不大。由于所设计结构的芯子参数变化对芯子抗剪性能的影响在小跨距条件下更为显著,因此对上、下两层波纹角度和方向进行讨论,探究其对结构弯曲性能的影响。

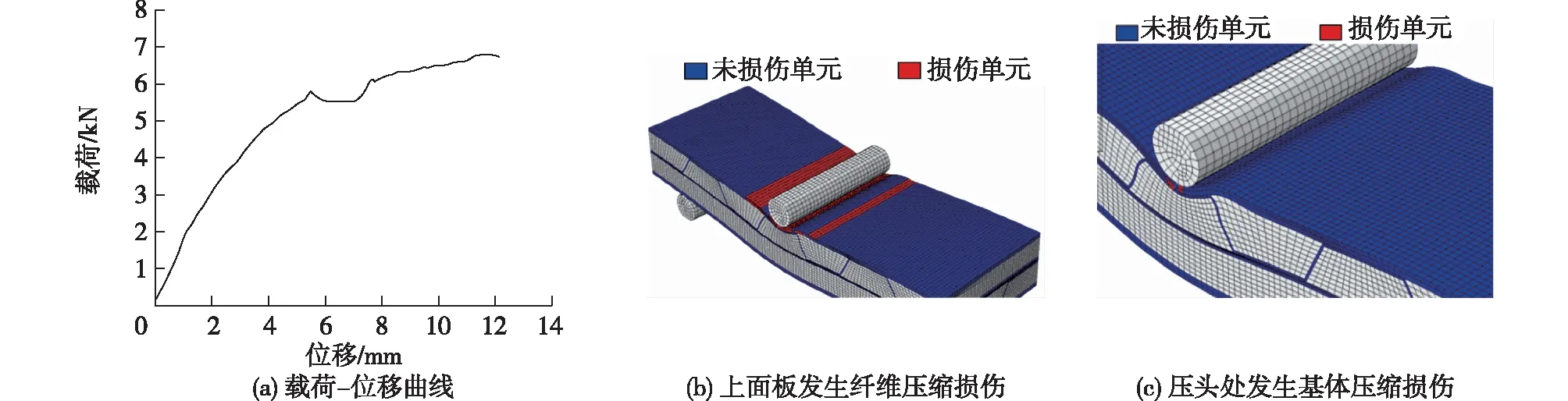
图10 加载点位于波峰处的模拟结果Fig.10 Simulated results of loading point at wave crest

2.3 波纹方向对结构弯曲性能的影响

双层波纹夹芯结构包含两层增强波纹,当波纹板的增强方向与试样长度方向一致时,试样弯曲性能增强效果较好,否则增强效果较差。将单向增强波纹板置于受拉侧的命名为模型A,置于受压侧的命名为模型B(图11),探索波纹方向对双层波纹板弯曲性能的影响。对于模型A,上、下两层波纹的波纹角度均为60°,采用前文所述有限元分析方法对两个模型进行计算,得到的载荷-位移曲线以及损伤变量云图如图12所示。

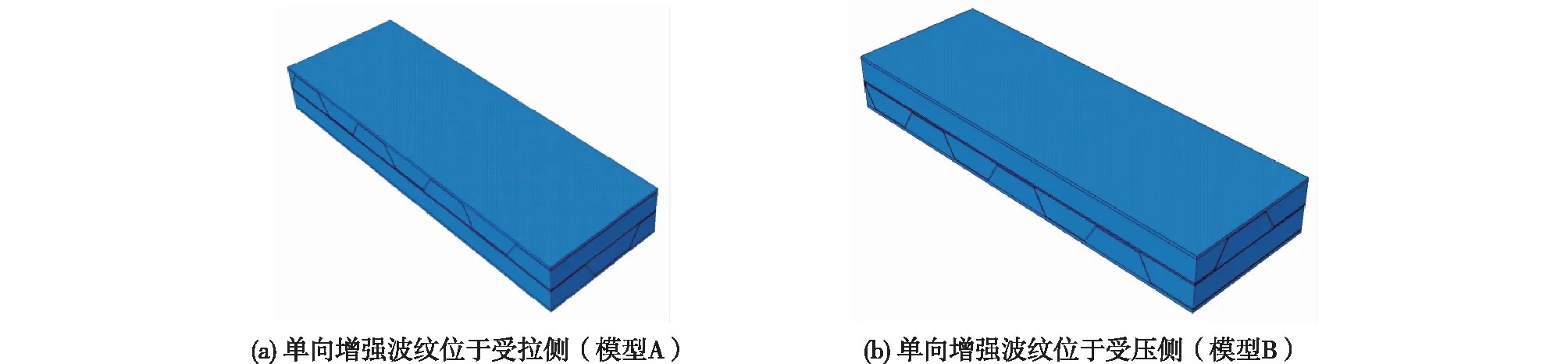
图11 单向增强波纹位于不同侧的模型Fig.11 Models of unidirectional reinforced corrugation on different sides

图12 模型计算所得载荷-位移曲线和损伤变量云图Fig.12 Load-displacement curves and cloud diagram of damage variables calculated by models

由图12(a)可以看出:模型A的初始失效载荷为5.07 kN,模型B的初始失效载荷为11.64 kN,即纵向波纹位于加载侧时的初始失效载荷提高了129.59%。通过计算可得模型A和B的弯曲刚度分别为5.62×108和7.03×108N·mm2，即纵向波纹位于加载侧时的弯曲刚度提高了25.09%,这是因为波纹板的峰值载荷所对应的失效模式是上面板发生纤维压缩损伤,对于模型A而言,上面板主要承担压头载荷;对于模型B而言,除了上面板以外,波纹芯子也参与了承载,即波纹芯子对上面板有增强作用,故导致模型B的承载能力大于模型A的承载能力。同时,模型A和B的结构总体厚度一致,结构抗弯截面模量相差不大,导致两个模型的背板变形相差不大,所以模型A的弯曲刚度小于模型B的弯曲刚度。由图12(b)和12(c)可以看出:模型A和B的失效模式均为上面板的纤维压缩失效。综上所述,对于双层波纹夹芯结构的两种模型(梁结构),当纵向增强波纹位于受压侧时弯曲性能更优。

2.4 波纹角度对结构弯曲性能的影响

对于模型A,设置下层纵向波纹角度为60°,固定不变;上层横向波纹角度依次设置为40°、50°、60°和70°,计算结果如表4所示。另外，设置上层横向波纹角度为60°不变时,下层纵向波纹角度依次设置为40°、50°、60°和70°,计算结果如表5所示。

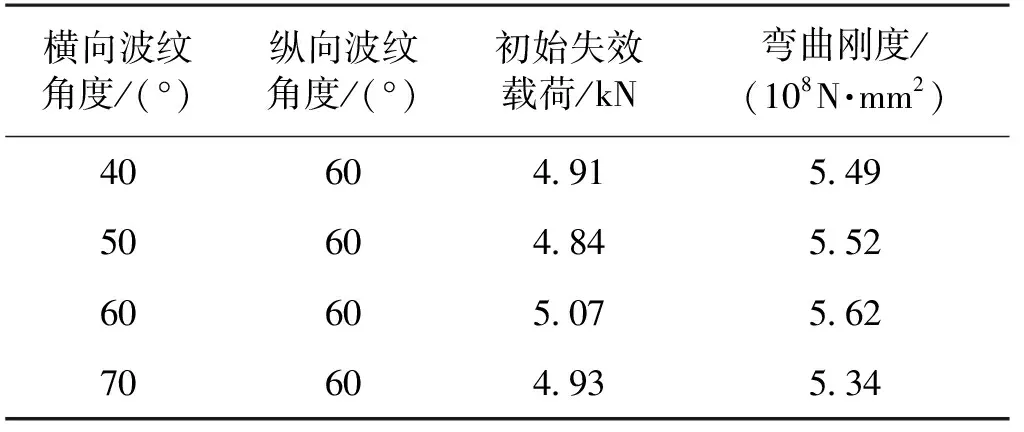
表4 改变模型A横向波纹角度的计算结果

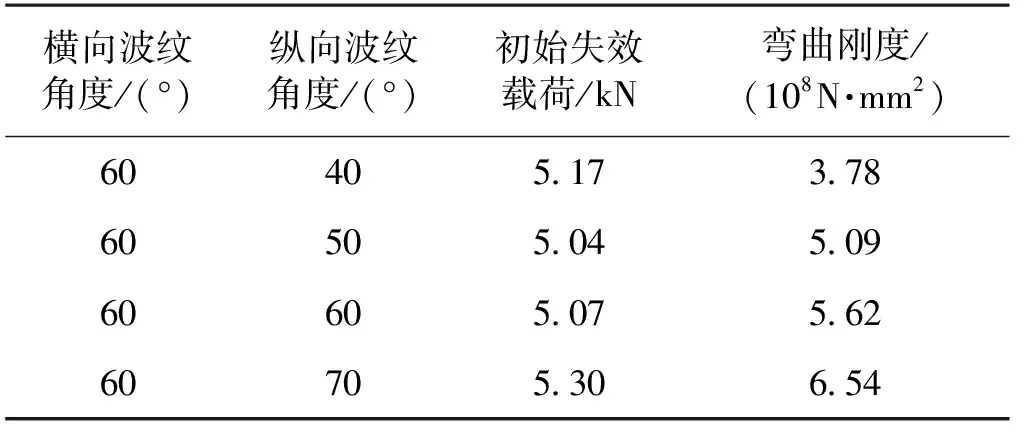
表5 改变模型A纵向波纹角度的计算结果

由表4可知:对于模型A,上层横向波纹角度的变化对双层波纹夹芯结构的初始失效载荷和弯曲刚度影响不明显,这是因为在达到峰值载荷时,失效模式是上面板发生纤维压缩损伤,模型A的上面板主要承担压头载荷,波纹芯子对上面板没有增强作用,故改变波纹角度无法改变其承载能力,而改变上面板厚度可以有效提高模型A的承载能力。由表5可知:下层纵向波纹角度的改变对结构的初始失效载荷影响不大,但对结构的弯曲刚度影响较大,且随着纵向波纹角度的增大,弯曲刚度随之增大,这是因为双层波纹板以上面板的局部损伤为主要失效模式,导致改变下层纵向波纹角度对初始失效载荷的影响较小。然而,随着下层纵向波纹角度的增大,使得双层波纹板的抗弯截面模量增大,造成双层波纹板背板变形减小,故随着下层纵向波纹角度的增大,模型A的弯曲刚度逐渐增大。

参照模型A的研究方法,对模型B开展研究,即当横、纵向波纹角度分别取60°时,另一层波纹角度取40°、50°、60°和70°,计算得到双层波纹夹芯结构的初始失效载荷和弯曲刚度,结果如表6和7所示。

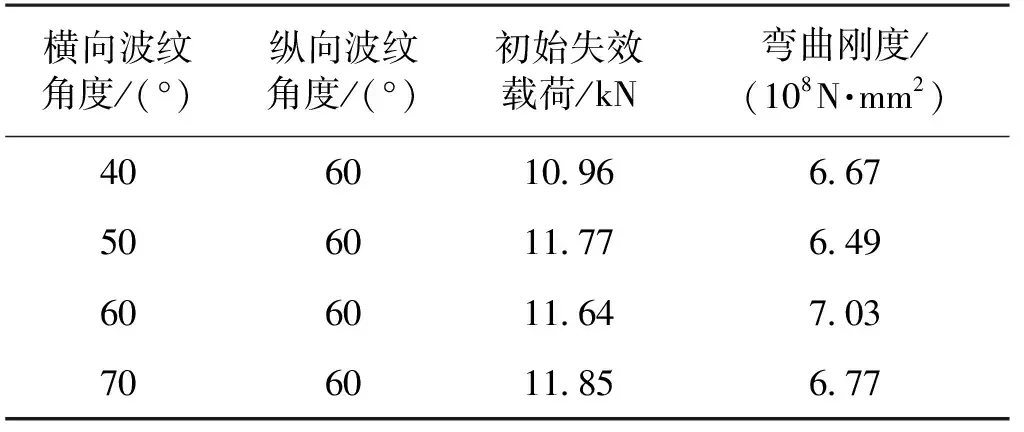
表6 改变模型B横向波纹角度的计算结果

表7 改变模型B纵向波纹角度的计算结果

由表6可知:对于模型B,下层横向波纹角度的变化对双层波纹夹芯结构的初始失效载荷影响不明显,对结构弯曲刚度有一定影响,这是由于下层横向波纹主要参与结构受载变形,随着波纹角度的变化,抗弯截面模量发生变化。由表7可知:上层纵向波纹的角度变化对双层波纹夹芯结构的初始失效载荷和弯曲刚度影响均较大,且随着纵向波纹角度的增大,初始失效载荷和弯曲刚度随之增大,这是因为在载荷作用下模型B的失效过程中,除了上面板以外,波纹芯子也参与了承载,上层纵向波纹角度增大使得双层波纹板的抗弯截面模量增大,从而使得结构的弯曲性能得到提升,结构的承载能力也有一定增大。结合表5分析发现:对于本文所设计的双层波纹夹芯结构,无论是模型A或B,增大纵向波纹角度均可以增大整体结构抗弯截面模量,使得结构的弯曲刚度增大,即两种结构的纵向波纹角度与结构弯曲刚度是正相关的。此外,两种模型的失效载荷变化主要与结构的失效模式有关。

3 结论

1)双层波纹夹芯结构试样在三点弯试验中,呈现的主要失效模式为上面板和中间面板先后发生压溃,基于损伤扩展的有限元方法对结构进行数值模拟,模拟与试验所得极限承载力和弯曲刚度的误差分别为10.14%和9.98%,有限元模拟的失效模式与试验所得结果一致,验证了数值模拟的可靠性。

2)加载位置的不同,对结构的极限承载力有一定影响,但对弯曲刚度的影响不大。当加载处有波纹支撑时,压头下方树脂基体会发生压缩失效。

3)对于双层波纹夹芯结构的两种模型,当纵向波纹位于加载侧时的初始失效载荷和弯曲刚度比横向波纹置于加载侧时高出分别提高了129.59%和25.09%。

4)对于双层波纹夹芯结构(梁结构),当横向波纹位于结构下层时,随着波纹角度的增大,结构的弯曲刚度增大;而无论纵向波纹层置于结构上层或下层时,增大纵向波纹角度均可以提升结构的弯曲刚度。当纵向波纹置于受压侧时,增大纵向波纹角度能够提高结构的承载能力。