The generating fields of two twisted Kloosterman sums
ZHANG Shenxing
CAS Wu Wen-Tsun Key Laboratory of Mathematics, School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China
Abstract: The generating fields of the twisted Kloosterman sums Kl (q, a, χ) and the partial Gauss sums g(q, a, χ) are studied.We require that the characteristic p is large with respect to the order d of the character χ and the trace of the coefficient a is nonzero.When p≡±1 mod d,we can characterize the generating fields of these character sums.For general p,when a lies in the prime field,we propose a combinatorial condition on (p, d) to ensure one can determine the generating fields.
Keywords: Kloosterman sum; exponential sum; cyclotomic field; algebraic number
1 Introduction
1. 1 Background


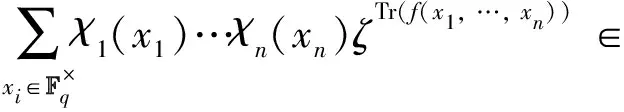
wheredis the least common multiplier of orders ofχ1, …,χn,ζis a fixed primitivep-th root of unity and Tr=Tr. If allχiare trivial andfis a polynomial,we denote by
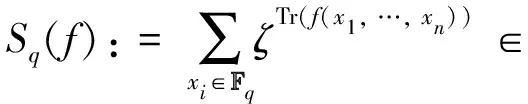
the exponential sum off. Ifζis replaced by another primitivep-th root of unity,the twisted exponential sum is replaced by a Galois conjugate and its degree does not change. There are various results about estimation on the exponential sums,their absolute values andp-adic valuations we will not list here. What we will discuss is their generating fields for some specialf,χi.

① degf=1:Sq(f)=0.

Sq(x2)=(-1)k-1Sp(x2)k.
HenceSq(x2+a)=(-1)k+1Sp(x2)kζTr(a)and

See Ref.[2, Example 3.10].
④f=axdd2+xdd1with coprimed1,d2: Ifp≡1 modd,pis large with respect to degfand Tr(a-d1)≠0, then
See Ref.[3, Theorem 1.1].
⑤ Forf∈q[x], (p-1)/degSp(f) is a factor of

See Ref.[2, Theorem 3.16].
⑥ The sequence {Sqk(f)}kis periodic fork≥Nfor some constantN,see Ref.[4, Theorem 1]. Zhang gave a bound on the period in Ref.[3, Corollary 2.4]. Combining this result and the bound on the degree of theL-function offin Ref.[5, Theorem 1], Zhang showed that: under certain coprime condition, the degree ofSpk(axd+1+x)=(p-1)/dfor sufficiently largekifp≡1 moddandpis large with respect tod. See Ref.[3, Corollary 1.2(2)].
The exponential sum of
is called the Kloosterman sum Kln(q,a). When Tr(a)≠0,the degree of Kln(q,a) is (p-1)/(n+1,p-1),see Ref.[6, Theorem 1.1]. When Tr(a)=0,the degree offcan be obtained by the work in Ref.[7, Corollary 4.24] and [6, Theorem 5.1] ifpis large orpdoes not divide a certain integer,with respect tonandk.But no simple formula is known in general,see also Ref.[8, Theorem 2].
1.2 Main results
We see that all of these results are about untwisted exponential sums. In this article,we will consider the generating field of the general Kloosterman sum
Kln(χ1, …,χn;d1, …,dn)(q,a)=


When Tr(a)≠0,we study the generating field of the twisted Kloosterman sum
Kl(q,a,χ):=Kl2(χ,1;1,1)(q,a)=
and the generating field of the partial Gauss sum
g(q,a,χ):= Kl1(χ;q+1)(q2,a)=
These character sums are motivated from the exponential sums of cubic polynomials. Whenχis cubic,the exponential sum
See Proposition 2.1.
Fix isomorphisms
σ-:(/p)×→Gal((μp)/)
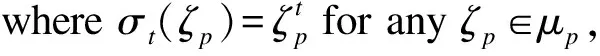
τ-:(/d)×→Gal((μd)/)
whereτw(ζd)=ζdwfor anyζd∈μd. Bothσtandτwcan be viewed as elements in Gal((μdp)/) sincepd.
Theorem 1.1Letdbe the order ofχ.
① Whend=2,
· Kl (q,a,χ)=0 ifχ(a)=-1;
· Kl (q,a,χ) generates(μp)+ifχ(a)=1,χ(-1)=1 and
· Kl (q,a,χ) generates(μp) ifχ(a)=1,χ(-1)=-1 and.
② Whend≥3 andp>5d-2, Kl(q,a,χ) generates(μdp)H,where
ifp≡±1 moddand Tr(a)≠0.
See Propositions 3.1 and 3.4.
Theorem 1.2Letdbe the order ofχ. Assume that Tr(a)≠0.
① Ifd|(q-1) andp>2,theng(q,a,χ) generates(μdp)H,where
H={τwσ±1|w≡1 modd1}
andd1|dis the order ofa(q-1)/d.
② Ifd|(p+1) andp>7d-2,theng(q,a,χ) generates(μdp)H,where
See Propositions 4.1 and 4.4.
For generald,if (p,d) satisfies a combinatorial condition,we characterize the generating fields of these character sums whena∈p. Letnbe the order ofpmodd. For anyr∈or/d,writeaj≡rp-jmoddwith 0≤aj≤d-1. Define
where
Denote by
Tp, d={r∈(/d)×|Vrs=Vs,∀s∈(/d)×}.

① Ifd≥3,p>5d-2 andTp, d=〈-1,p〉,then Kl(q,a,χ) generates(μdp)H,where
In particular,this holds ford≤31 withp≢±(d/2+1) moddif 4|d.
② Ifd|(q+1),p>7d-2 andTp, d/(2, d)=〈p〉,theng(q,a,χ) generates(μdp)H,where
In particular,this holds ifd/(2,d)≤31.
See Theorems 3.1 and 4.1.
It’s an interesting phenomenon that these two different Kloosterman sums depend on similar conbinatorial conditions. It seems that there should be a direct relation between these two Kloosterman sums.
We will express the Kloosterman sums as a Fourier expansion and use Stickelberger’s congruence theorem to determine the first several terms of the P-adic expansions for a fixed prime P in(μ(q-1)p). The main estimation is in Lemma 3.3. Then the generating fields are obtained by these results.
2 Preliminaries
2.1 The Stickelberger’s congruence theorem
We will use this theorem to estimate the valuations of Gauss sums. The primepsplits intof=φ(q-1)/kprimes as
p[μq-1]=p1…pf
pi

Letκbe the residue field of p andωthe Teichmüller lifting of the quotient map[μq-1]×→→κ×associated to p. We can viewωas a character onif we fix an isomorphismq≅κ. Different choice of the isomorphism may cause a composite by a power of the Frobenius map. Takeω(0)=0 for convention. Thenωis multiplicative and
ω(a)+ω(b)-ω(a+b)∈p.
In particular,its P-adic valuation is at leastp-1. Denote by
the Gauss sum ofω-m. Clearly,g(0)=-1 andg(pm)=g(m). Recall the Stickelberger’s congruence theorem,see Ref.[10;11,Chap.6].
Theorem 2.1For 0≤m where m=m0+m1p+…+mk-1pk-1, 0≤mi≤p-1. In particular,v(g(m))≡mmod (p-1) has same parity withm. In this subsection,we will show the relations between the cubic exponential sums and the twisted Kloosterman sums or the partial Gauss sums. This fact is well known to experts. Let’s show it briefly. ① Ifq≡1 mod 3,then Sq(x3-3ax)=Kl(q,a3,χ) From this,Sq(x3-3ax) generates (μp)+=(ζ+ζ-1) if Tr(a3)≠0 andp>19. ProofDenote byNcthe number of the equation f(x)=x3-3ax=c∈q with multiplicities.The discriminant off-cis ·Nc=1,f-cdecomposes into a linear factor and a degree 2 irreducible polynomial.Thus the splitting field off-cisq2andq. ·Nc=0,f-cis irreducible and Fix a nontrivial cube root of unityλ∈q2. Then. ① In this case,λ∈q. Assume thatThat’s equivalently to say,Nc=0 or 3. By Cardano’s formula,the solutions off(x)=cinqare u+au-1,λu+λ2au-1,λ2u+λau-1, Then and Ifa∉q×2,the termsζTr(±2a3/2)disappear. Now Sq(f)=B1+3B3+2ζTr(2a3/2)+2ζTr(-2a3/2)= 2B3-B0+ζTr(2a3/2)+ζTr(-2a3/2)= ζTr(2a3/2)+ζTr(-2a3/2)= by Lemma 3.1①. ② In this case,p≡-1 mod 3,k=2l+1 is odd andλ∈q2-q. Thus -27 is not a square inq. Assume that (2λ+1)∈q. That’s equivalently to say,Nc=0 or 3. Letδ:xxqbe the nontrivial element in Gal(q2/q). The solutions off(x)=cinqare u+uδ,λu+λ2uδ,λ2u+λuδ, by Lemma 4.1①. Finally,the claim on the generating field ofSq(x3-3ax) follows from Propositions 3.4 and 4.4. Remark 2.1The condition onpcan be weaken top>11,see Ref.[3, Corollary 1.2]. In this section,we will study the generating field of the twisted Kloosterman sum whered|(q-1) is the order ofχ. Lemma 3.1We have ② Kl(q,a,χp)= Kl(q,ap,χ). ProofWe substitutexbya/xorxprespectively,then the result follows. There is an integerwprime todsuch thatχ=ω-(q-1)w/d. Then Kl(q,a,χ)=τwKl(q,a,ω-(q-1)/d). Since we are interested in the generating field of Kl(q,a,χ),we may assume thatχ=ω-(q-1)/dfrom now on. Lemma 3.2We have a Fourier expansion ProofWe have Thus Proposition 3.1Assume thatd=2. ① Kl(q,a,χ)=0 ifχ(a)=-1. ② Writea=b2.By Lemma 3.2, we have Write with 0≤mj,nj≤p-1. Then and The equality holds if and only allm′j=′j=0,that′s to say,m=0. There are two cases such that the valuation is secondly minimal. (i) Allm′j=′j=0 exceptm′i=1 for a uniqueiwith 0≤i≤k-1. That’s to say,m=pi, m+(q-1)/2≡pi(q+1)/2 mod (q-1). The summation of Fourier terms over thesemis (ii) Allm′j=′j=0 except′i=′i′=1 for a unique pairi,i′ with 0≤i m+(q-1)/2≡(pi′+pi+k)/2 mod (q-1). The summation of Fourier terms over thesemis Cω(Tr(b)2-Tr(b2))πV+2mod PV+3. Now we have (q-1) Kl(q,a,χ)≡ (1) Ifσtfixes Kl(q,a,χ),we have σtKl(q,a,χ)=χ(t)-1Kl(q,at2,χ)=Kl(q,a,χ) and thenχ(t)=1, ω(Tr(bt))2≡ω(Tr(b))2mod P. Note that Tr(b)≠0. Ifχ(-1)=-1,we havet=±1 and Kl(q,a,χ) generates(μp)+. Ifχ(-1)=1,we havet=1 and Kl(q,a,χ) generates(μp). We need the following lemma to obtain the P-adic expansion of Kl(q,a,χ). Lemma 3.3Let be an integer less thanq-1,satisfyingsj≠(p-1)/2 for allj. Denote by and V:=v(g(M)g(M+s))= where Considerv(g(m)g(m+s)) for 0≤m ① If |(p-1)/2-sj|>1 for allj,then the valuation is minimal:m=M,v=V. ② If |(p-1)/2-sj|>2 for allj,then the valuation is secondly minimal:m≡M+pimod (q-1) for somei,v=V+2. ③ If |(p-1)/2-sj|>3 for allj,then the valuation is thirdly minimal:m≡M+pi+pi′mod (q-1) for somei,i′,v=V+4. ProofDenote bysj′=min{sj,p-1-sj}. Write m+s-(q-1)k-1= nj=mj+sj+j-1-pj, whereδj′=δj-j. Assume that |(p-1)/2-sj|>λfor allj. ① Placeδ′0, …,δ′k-1in a circle. If allδ′j=0, Otherwise there areαstrings of ±1’s,with total lengthz. Ifδ′j=δ′j+1=0,then′j=|δj-δj+1|. Thus V+2λz-2z=V+2(λ-1). Therefore,v(g(m)g(m+s))≥Vwith equality holds if and only ifm=M. ② Note that the valuation has same parity withs. Whenz≥1,we have thatv(g(m)g(m+s))>V+2. Thus the valuation is secondly minimal if and only if allδ′j=0 and only onemi′=1. The result then follows. ③ Whenz≥1,we have thatv(g(m)g(m+s))>V+4. Thus the valuation is thirdly minimal if and only if allδj′=0,m′i=2 for someiorm′i=m′i′=1 for somei≠i′,and other entries are zero. The result then follows. Definition 3.1Letpbe a prime prime tod. Letnbe a positive integer such thatpn≡1 modd. For anyr∈or/d,writeaj≡rp-jmoddwith 0≤aj≤d-1. Define (2) where This definition does not depend on the choice ofn. Proposition 3.2Ifp>3d-2,then the valuation of Kl(q,a,χr) iskVr. ProofIfr≡d/2 modd,Vr=(p-1)/2 and the valuation of Kl(q,a,χr)= Kl(q,a,ω(q-1)/2)= is (p-1)k/2 by Equation(1). Ifr≢d/2 modd,thenaj≠d/2 and Thus satisfies the condition in Lemma 3.3① and then the valuation of Kl(q,a,χr) iskVrby Lemma 3.2. Definition 3.2For anys∈or/d,define Vrs=Vs}⊆(/d)× (3) Define Proposition 3.3Assume thatp>3d-2. ①Tp, dis a group containing {±pλmodd|λ∈}. ② Ifp≡±1 modd,thenTp, d={±1}. ③ If 4|d≥16 andp≡d/2±1 modd,thenTp, d=(/d)×. ④ If 3≤d≤31 and (p,d) does not satisfies ③,thenTp, d={±pλmodd|λ∈}. Proof① Ifr1,r2∈Tp, d,thenVr1r2-1s=Vr2-1s=Vs. Thusr1r2-1∈Tp, dandTp, dis a group. SinceV±pr=Vrby the definition,the groupTp, dcontains -1,p. ② That’s because ifp≡±1 modd,we have (4) ③ Ifp≡d/2±1 modd,then ThusVr=(p±1)k/4 andTp, d=(/d)×. When 4|d≥16,φ(d)>4. HenceTp, ddoes not equal 〈-1,p〉. ④ We have already know the casep≡±1 moddin ②. Clearly the assertion holds ifpand -1 generate (/d)×. The rest cases are listed in Table 1. Table 1. Vrfor d≤32, (r, d)=1. ③ It seems thatTp, d=Tp′, difp′≡pmoddand bothp,p′>3d-2. But I do not have a proof or a counterexample. Proposition 3.4Assume thatd≥3 andp>5d-2. Ifp≡±1 moddand Tr(a)≠0,then Kl(q,a,χ) generates(μdp)H,where ProofWe may assume thatχ=ω-(q-1)/d. Denote byMrtheMin Lemma 3.3 fors=(q-1)r/d. By Lemma 3.3 and Proposition 3.2, we have (q-1)Kl(q,a,χr)≡ CπkVr+2ωMr(a)ω(Tr(a)) mod PkVr+3 (5) whereCis a constant prime top. By Lemma 3.1①,we have τwσtKl(q,a,χ)=χ(t)-wKl(q,t2a,χw)= χ(ta)wKl(q,t2a,χ-w) (6) Ifτwσtfixes Kl(q,a,χ),thenVw=V1. Thusw=±1 by Proposition 3.3②. Ifw=1,χ(t)-1Kl(q,t2a,χ)= Kl(q,a,χ) and we have χ(t)-1ωM1(t2a)≡ωM1(a) mod P. This forcesχ(t)-1ωM1(t2)=1 and then χ(t)-1ωM1(t2a)ω(Tr(t2a))≡ ωM1(a)ω(Tr(a)) mod P. Sinceω(Tr(a))≠0,we haveω(t2)=1,t=±1 andχ(t)=1. Ifw=-1,χ(ta)-1Kl(q,t2a,χ)= Kl(q,a,χ) and we have χ(ta)-1ωM1(t2a)≡ωM1(a) mod P. This forcesχ(ta)-1ωM1(t2)=1 and then χ(ta)-1ωM1(t2a)ω(Tr(t2a))≡ ωM1(a)ω(Tr(a)) mod P. Sinceω(Tr(a))≠0,we haveω(t2)=1,t=±1 andχ(ta)=1. The result then follows. In particular,this holds ford≤31 withp≢±(d/2-1)moddif 4|d. ProofIfτwσtfixes Kl(q,a,χ),it also fixesτrKl(q,a,χ)= Kl(q,a,χr). ThusVwr=Vrby Equations(5), (6) and Proposition 3.2. Thenw∈Tp, dandw≡±pλmoddfor someλ. Forw≡pλ,by Lemma3.1②,we have Kl(q,a,χw)= Kl(q,a,χpλ)= Kl(q,apλ,χ)= Kl(q,a,χ). Similar to the proof of Proposition 3.4, if Tr(a)≠0,we haveω(t2)≡1 and thent=±1,χ(t)=1. Forw≡-pλ,by Lemma 3.1②, we have Kl(q,a,χ-w)= Kl(q,a,χ). Similarly,if Tr(a)≠0,we havet=±1 andχ(ta)=1. The last claim follows from Proposition 3.3④. In this section,we will study the partial Gauss sum Lemma 4.1We have ②g(q,a,χp)=g(q,ap,χ). ③ Whendis even,we have g(q,a,χd/2+1)=χ2(a)g(q,a,χ), ProofWe substitutexbyxδ=a/xorxprespectively,then ① and ② follows.Ifxxδ=a,thenχd/2(x)=ω(q-1)/2(a)=χ2(a) and ③ follows. Similar to Section 3, we may assume thatχ=ω-(q2-1)/dsince we are interested in the generating field ofg(q,a,χ). Lemma 4.2We have a Fourier expansion (q-1)g(q,a,χr)= Thus We will consider the casesd|(q±1) respectively. Proposition 4.1Assume thatd|(q-1) andp>2. If Tr(a)≠0,theng(q,a,χ) generates(μdp)H,where H={τwσ±1|w≡1 modd1} andd1|dis the order ofa(q-1)/d. ProofWe have g(q,a,χr)=ω-(q-1)r/d(a)g(q,a,1) (7) and (q-1)g(q,a,1)≡ 1+ω(Tr(a))g(q+1) mod P3 (8) by Lemma 4.2. Since χ-w(t)g(q,at2,χw) (9) ifτwσtfixesg(q,a,χ),we have χ-w(t)ω-(q-1)(w-1)/d(a)=1. Thus we have ω(Tr(t2a))≡ω(Tr(a)) mod P. If Tr(a)≠0,thent=±1 andχ(t)=ω-(q-1)/d(tq+1)=1. Thenw≡1 modd1andg(q,a,χ) generates(μdp)H. We need the following lemma to obtain the P-adic expansion ofg(q,a,χ). Lemma 4.3Letsbe a positive integer less than (q-1)/2. Letsj,δj,M,Vbe the notations as in Lemma 3.3. Assume that |(p-1)/2-sj|>3 for allj;s0≥2 and not allδjare same. ① The valuationv(g((q+1)m+s)) is · minimal:m=M,v=V; · secondly minimal:m=M+pj,v=V+2. ② The valuationv(g((q+1)m-s)) is · minimal:m=M+s,v=V; · secondly minimal:m=M+s+pj,v=V+2. ProofBy the assumptions,p≥11 andsk-1≤(p-9)/2. Thens<(p-7)pk-1/2 and Thus M+2δ0-1+pi+pi′+s< (10) Denote bygqthe Gauss sum with respect toq. ① Ifm+s≥q,then v(g((q+1)m+s))=v(gq(m+s-q)gq(m+1))= v(gq(m+s-1)gq(m+1)). Sinces-2 has sameδisequence ass,by Lemma 3.3,the valuation is · minimal:m=M+2δ0-1,v=V+4δ0-2; · secondly minimal:m=M+2δ0-1+pi,v=V+4δ0; · thirdly minimal:m=M+2δ0-1+pi+pi′,v=V+4δ0+2. But by (10), these three cases do not happen and the valuation is at leastV+4. Ifm+s v(g((q+1)m+s))=v(gq(m)gq(m+s)). By Lemma 3.3, the valuation is · minimal:m=M,v=V; · secondly minimal:m=M+pi,v=V+2. The result then follows. ② Ifm v(g((q+1)m-s))= v(gq(m-1)gq(m+q-s))= v(gq(m′)gq(m′+s-2)), wherem′=m+q-s. Sinces-2 has sameδisequence ass,by Lemma 3.3, the valuation is · minimal:m=M+2δ0-1+s,v=V+4δ0-2; · secondly minimal:m=M+2δ0-1+s+pi,v=V+4δ0; · thirdly minimal:m=M+2δ0-1+s+pi+pi′,v=V+4δ0+2 by (10). Butm Ifm≥s,then v(g((q+1)m-s))=v(gq(m-s)gq(m)). By Lemma 3.3, the valuation is · minimal:m=M+s,v=V; · secondly minimal:m=M+s+pi,v=V+2. The result then follows. Proposition 4.2Ifp>7d-2,then the valuation ofg(q,a,χr) iskV2r. ProofIfr≡0,d/2 modd,thenV2r=0 and the order ofχris at most 2,which dividesq-1. Thus the valuation ofg(q,a,χr) is zero by (7) and (8). Ifr≢0,d/2 modd,by Lemma 4.1① and the fact thatV2r=V-2r,we may assume that 1≤r Then wherebjpj≡2rmoddwith 0≤bj≤d-1. By Lemmas 4.2, 4.3 and the valuation ofg(q,a,χr) iskV2r=kVd-2r. Definition 4.1Letp>7d-2 be a prime prime tod. V2rs=V2s,∀(s,d)=1}⊂(/d)×, Proposition 4.3Assume thatp>7d-2. ① Ifdis odd,thenT′p, d=Tp, d. Ifdis even,thenT′p, d={r|rmodd/2∈Tp, d/2}. ThusT′p, dis a group containing 〈d/2+1, -1,p〉. ② Ifp≡±1 modd,thenT′p, d={±1, ±(d/2+1)}. ③T′p, d=〈d/2+1, -1,p〉 if and only if Tp, d/(2, d)=〈-1,p〉. ④ If -1 is a power ofpmodd,thenT′p, d=〈d/2+1,p〉 ifd/(2,d)≤31. Here,d/2+1 appears only if 4|d. ProofNote that (d/2-1,d)=(d/2-1, 2)=1 holds only if 4|d. ① follows from the definition directly. ② follows from ① and Proposition 3.3②. ③ follows from ①. For ④,p≢±(d/4+1)modd/2 if 4|d/2≥16.Then the result follows from ① and Proposition 3.3④. Proposition 4.4Assume thatp>7d-2. Ifp≡-1 moddand Tr(a)≠0,theng(q,a,χ) generates(μdp)H,where ProofWe may assume thatχ=ω-(q2-1)/d. The casesd=1, 2 is shown in Proposition 4.1 and we may assume thatd≥3. (q-1)g(q,a,χr)≡ ωMr(a)g(Nr)+CπkV2r+2ωMr(a)ω(Tr(a)) mod PkV2r+3 (11) g(q,a,χ-r)=g(q,a,χr), g(q,a,χd/2±r)=χ2(a)g(q,a,χr). Ifτwσtfixesg(q,a,χ),then by (9),V2w=V2. Thusw≡±1, ±(d/2+1)moddby (4). Ifτ±1σtfixesg(q,a,χ),we have ωM1(t2a)≡ωM1(a) mod P. This forcesωM1(t2)=1 and then ωM1(t2a)ω(Tr(t2a))≡ωM1(a)ω(Tr(a)) mod P. Since Tr(a)≠0,we haveω(t2)=1 andt=±1. If 4|dandw=d/2±1,we haveχ2(a)=1 andσtfixesg(q,a,χ).Since Tr(a)≠0,we havet=±1. The result then follows. In particular,this holds ifd/(2,d)≤31. ProofIfτwσtfixesg(q,a,χ),it also fixes τrg(q,a,χ)=g(q,a,χr). ThusV2wr=V2rby (9), (11) and Proposition 4.2. Note that -1 is a power ofpmodulod. Thenw∈T′p, dandw≡pλor (d/2+1)pλmoddfor someλ. Forw≡pλ,by Lemma 4.1②,we have g(q,a,χw)=g(q,apλ,χ)=g(q,a,χ). Similar to the proof of Proposition 4.4, if Tr(a)≠0,we haveω(t2)=1 and thent=±1. For 4|dandw≡(d/2+1)pλmodd,by Lemma 4.1②③, we have g(q,a,χw)=χ2(a)g(q,a,χ). Thusχ2(a)=1 by (11). Similarly,if Tr(a)≠0,we havet=±1. Acknowledgments This work is supported by the NSFC (No. 12001510), the Fundamental Research Funds for the Central Universities (No. WK0010000061) and Anhui Initiative in Quantum Information Technologies (No. AHY150200). The author would like to thank WAN Daqin, OUYANG Yi and XU Yue for many helpful suggestions and discussions. Conflictofinterest The author declares no conflict of interest. Authorinformation ZHANGShenxingis a post-doctoral fellow at the University of Science and Technology of China. He received his PhD from the University of Science and Technology of China, under the supervision of Professor OUYANG Yi. His research interests focus on elliptic curves, class groups and character sums.2.2 Relation to the exponential sums of cubic polynomials












3 The twisted Kloosterman sums
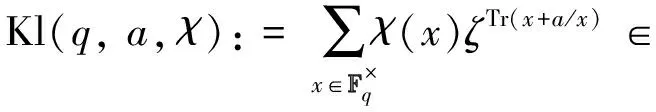

3.1 The quadratic twist
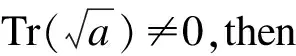
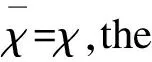




3.2 The d-th twist with d≥3









4 The partial Gauss sums





4.1 The case d|(q-1)
4.2 The case d|(q+1)




