Statistical test for high order stochastic dominance under the density ratio model

ZHOU Yang, QIU Guoxin, ZHUANG Weiwei

1. School of Management, University of Science and Technology of China, Hefei 230026, China;2. School of Business, Xinhua University of Anhui, Hefei 230088, China;3. International Institute of Finance, School of Management, University of Science and Technology of China, Hefei 230061, China

Abstract: In economics, medicine and other fields, how to compare the dominance relations between two distributions has been widely discussed. Usually population means or medians are compared. However, the population with a higher mean may not be what we will choose, since it may also have a larger variance. Stochastic dominance proposes a good solution to this problem. Subsequently, how to test stochastic dominance relations between two distributions is worth discussing. In this paper, we develop the test statistic of high order stochastic dominance under the density ratio model. In addition, we provide the asymptotic properties of test statistic and use the bootstrap method to obtain p-values to make decisions. Furthermore, the simulation results show that the proposed test statistics have the high test power.

Keywords: stochastic dominance; density ratio model; bootstrap test; empirical likelihood

1 Introduction

Stochastic dominance (SD) is a method based on the expected utility theory, which can sort stochastic variables and reduce the effective set to help investors to make decisions. Stochastic dominance theory was originally proposed by Lehmann[1]. Later, Hadar and Russell[2], Hanoch and Levy[3], Rothschild and Stiglitz[4], and other scholars applied stochastic dominance theory and criteria to practice. Some scholars combined stochastic dominance with statistics to consider testing stochastic dominance. Regarding the test of stochastic dominance, it can be roughly divided into two categories: comparing the distributions at a finite number of grids, and comparing the distributions over the whole support. For the first type of test statistics, Anderson[5]established a test based on thet-statistic for two independent populations. Although their test statistic follows a normal distribution, the test power is not high. Davidson and Duclos[6]based on Anderson’s test, used a new method to handle finite data. For the latter, McFadden[7]proposed the KS statistic to test first degree stochastic dominance, but the sample sizes of two populations are required to be equal. Eubank et al.[8]put forward a second degree stochastic dominance test, but the null hypothesis is that the distributionFdominates a known distributionF0. In reality, both distributions may be unknown. Kaur et al.[9]advised to use the infimum of distributions to test the dominance relations. The advantage of this method is that the limiting distribution of test statistic can be given. However, the disadvantage is that if one distribution almost dominates the other one, the null hypothesis cannot be rejected. Schmid and Trede[10]proposed a test for second degree stochastic dominance and gave its critical value, but the test required one known distribution with the monotonically decreasing density. The strict assumption results in the narrow scope of application. Barrett and Donald[11]presented a test statistic based on KS and gave its asymptotic distribution. Donaid and Hsu[12]offered a method to improve the power of stochastic dominance test. Estimators chosen in these papers generally used empirical distributions. Such nonparametric methods sometimes may have large errors. Especially, in reality, the populations under comparison are usually of the same nature: In economics, they can be income distributions of several socio-demographic groups; in finance, they can be asset return distributions. In these cases, the density ratio model (DRM) provides a semiparametric model to connect these populations. When the density functions of populations meet certain assumptions, we can estimate each cumulative distribution function based on the pooled sample, therefore this model can improve estimation efficiency compared to that of nonparametric model[13-19].

The DRM originated from the logistic discriminant analysis of Anderson[20,21]. Anderson[13]formalized this model by setting the ratio of density functions of certain samples with similar information as the parameters family. Owen[22,23]proposed that the empirical likelihood can effectively handle the basic function in the DRM. Qin and Zhang[14]showed that the DRM could be used to solve the case-control logistic regression problem, estimated the parameters in the DRM using empirical likelihood, and finally gave a test to illustrate the feasibility. Qin[24]applied the DRM to the expected likelihood of case-control data. Keziou and Leoni-Aubin[15]formally equated the maximum empirical likelihood estimation of the parameters in the density ratio model with the maximum dual likelihood estimation. The dual empirical likelihood can be written as a specific expression, so it is more convenient to calculate and apply. Chen and Liu[16]gave the asymptotic distributions of quantile estimations based on the DRM. Zhuang et al.[25]estimated the relaxation indexes of stochastic dominance under the DRM. Compared with parametric models with the given distributions, the DRM can compensate for the loss of distribution errors and effectively reduce the risk of misprediction of the model distributions. Meanwhile, compared with nonparametric models, the DRM can make full use of similar information by making fewer assumptions, and improve the estimation accuracy.

In this paper, we use a semiparametric method to estimate the distribution functionsFandGby using the empirical likelihood under the DRM. Based on the resulting estimators, we propose the test statistics of high order stochastic dominance, obtain the asymptotic properties of the test statistics, and construct the critical values. We conduct inferences of the test byp-value simulation using the bootstrap method. We select normal distributions and gamma distributions for the artificial data simulation, and use an actual example of stocks to illustrate the validity of our test. Simulation studies show that our test statistics substantially improve the estimation efficiency compared to the test statistics based on empirical distributions.

The rest of paper is organized as follows. In Section 2, a brief introduction of stochastic dominance and the DRM is given. In Section 3, our test statistics of high order stochastic dominance are proposed, the asymptotic properties of the test statistics are given, and a bootstrap method is developed to obtainp-values to make decisions. In Section 4, we apply our method to analyze two artificial examples and one actual example of stocks. Section 5 concludes the paper.

2 Notations and definitions

2.1 Stochastic dominance

Here are three commonly used dominance relations: first degree stochastic dominance (FSD), second degree stochastic dominance (SSD) and third degree stochastic dominance (TSD). As a simple example, if the return of the assetXin any case is higher than that of the assetY, we will choose the assetXwithout hesitation. This is the simplest FSD relationship, but the conditions of FSD are too strict and hard to meet in daily life. Compared with FSD, SSD is more common, and it is aimed at the avaricious and risk averse people. TSD is aimed at the investors who are not only avaricious and risk averse, but also have diminishing levels of risk aversion. Let the cumulative distribution functions of random variablesXandYbeFandG, respectively. Now we give the definition of stochastic dominance. Before giving the definition, we need to make the following assumptions:Assumption 2.1Assume that:

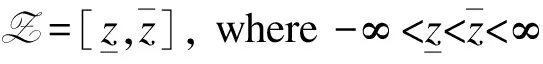
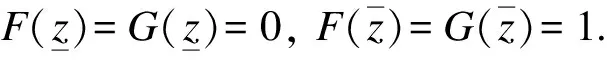
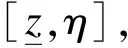
Next, we give the definition of stochastic dominance.

Definition 2.1[6]Forj≥1,Fis said to dominateGof orderj, denoted byFjG(XjY), if and only if

Fj(z;F)≤Fj(z;G), ∀z∈Z

(1)

where

F1(z;H)=H(z),

In order to make the concept better understood, we give the following figures of FSD and SSD.

Figure 1. F (red line) and G (green line) satisfying FSD relationship.

Figure 2. F (red line) and G (green line) satisfying SSD relationship.

It can be seen from Figures 1 and 2 that the area ofFbelowGis always more than the areaFaboveG. It is worth mentioning that stochastic dominance of different orders satisfies the following relationship:

FSD⟹SSD⟹TSD

(2)

But the reverse is not true. The relationship (2) implies that we can test from low order to high order. If there is dominance relationship in the low order case, the high order dominance naturally exists. However, even if the higher order dominates, the lower order may not hold.

2.2 Density ratio model

In this subsection, we first briefly introduce the density ratio model. Suppose thatF0,F1, …,Fm,m≥1, are continuous cumulative distributions. These distributions are said to satisfy the density ratio model if they are linked through

(3)

Givenk=0, 1,…,m, supposenk>0 is the number of observations fromFk, andxkjrepresents thejth observation value fromFk(j=1,2,…,nk). Givenk,xk1,xk2, … ,xknkare independent and identically distributed. The total number of observations isn=n0+n1+…+nm, and denoteρk=nk/n(k=0, 1,…,m) as the sample proportion. We first estimate the model parametersθandF0through maximum likelihood estimation.

Letpkj=dF0(xkj). We have the log empirical likelihood function[27]:

(4)

(5)

(6)

Assumption 2.2[16]Assume that

④ the components ofq(x) are linearly independent and its first element is one.

Ω=(ωri, rj(xi,xj))1≤i≤j[16].

The analytical expression ofΩis complex, and the (r,s)th entry ofΩis determined as follows. Denotex∧y=min{x,y}. Letδrs=1 ifr=s, and 0 otherwise. Let

Then, the generic form ofωri, rj(xi,xj) is

ωrs(x,y)=σrs(x,y)-

(7)

where

andBr(x) is a length-dvector, with itssth segment being

3 Test statistics and asymptotic properties

Select two different continuous distributionsFrandFs(r≠s) from the distributions in the DRM. For the convenience of presentation, letFdenoteFr, and letGdenoteFs. To test thejth order dominance relations betweenFandG,j≥1, we first formulate the null and alternative hypotheses as follows:

Barrett and Donald[11]and Donald and Hsu[12]considered the same hypotheses. They used empirical distributions to estimate the distribution functionsFandG. AssumeX1,X2,…,XNandY1,Y2,…,YMare independent and identically distributed samples fromFandG, respectively. Their test statistics are defined as

(8)

However, in applied problems, the populations under comparison are generally of the same nature: In economics, they can be income distributions of several socio-demographic groups[5,6,29]; in finance, they are often asset return distributions[30,31]. In these cases, the density ratio model provides a semiparametric model to connect these populations. When the density functions of populations meet certain assumption, we can estimate each cumulative distribution function based on the pooled sample, therefore this model can improve estimation efficiency compared to that of nonparametric model[15-19].

(9)

In order to state the properties of test statistics, we first introduce the following lemma.

(10)

F1(x;F)=F(x),

and

Suppose

We want to prove

Note that

By mathematical induction, the lemma is proved.

Next, we study the asymptotic properties of our test statistics. Before giving the theorem, we introduce the following notation. Let

which converges weakly to a Gaussian processW(x) in any finite dimensional distributions under Assumption 2.2[16]. The Gaussian processW(x) has a continuous sample path, mean zero and covariance function

Cov(W(x),W(y))=ωrr(x,x)+

ωss(y,y)-ωrs(x,y)-ωsr(y,x)

(11)

where theωrsare given in (7). Whenx=y, we obtain the variance function

Var{W(x)}=

ωrr(x,x)+ωss(x,x)-2ωrs(x,x)

(12)

Theorem 3.1Suppose thatF0,F1,…,Fmare continuous population distributions satisfying the DRM. For any 0≤r,s≤m, we denoteFr=FandFs=G. Let

[Fj(·;F)-Fj(·;G)]},j≥1.

Then, under Assumption 2.2, we have

Ω1(x,y,W)=

ωrr(x,x)+ωss(y,y)-ωrs(x,y)-ωsr(y,x).

ProofFirst, we need to show that for anyj≥1,

(13)

The casej=1 is obvious. Forj=2, note the fact that

Consequently,

Now assume that whenj=k,k>2, we have

Thus, whenj=k+1,

Therefore, (13) is proved.

Next, it is easy to see from (10) that, for anyj≥1,

Fj(z;Wn)

(14)

Under Assumption 2.2, it is known from Chen and Liu[16]thatWnweakly converges to the Gaussian processWin any finite dimensional distributions. Since Fjis a continuous function, it can be seen from Continuous Mapping Theorem[32]that Fj(z;Wn) weakly converges to Fj(z;W). Especially, whenj=1, F1(·;W)=W. From (11), we have known that,Wis the Gaussian process with mean zero and covariance function

Ω1(x,y,W)=

ωrr(x,x)+ωss(y,y)-ωrs(x,y)-ωsr(y,x).

Then, this theorem is proved.

For anyj≥1, we choose the critical valuescjsatisfying

The following theorem presents asymptotic power properties of our test.

Theorem 3.2Suppose the same conditions as in Theorem 3.1, andcjis a positive finite constant. Then, forj≥1, we have

(15)

(16)

Part (i) is proved.

Next, we prove the second part. If the alternative hypothesis is true, there exists somez*∈Z such that

Fj(z*;F)-Fj(z*;G)=δ>0.

Thus,

It follows from Bahadur representation of DRM-based estimator[16]that

and

From (14), note that

Then, this theorem is proved.

The inequalities in (i) imply that the tests will never reject more often thanα. Moreover, the result in (ii) implies that the tests are capable of detecting any violation of the full set of implications of the null hypothesis.

4 Simulation results

Although in the previous section, we construct the critical valuecjfor the test, the value ofcjis difficult to obtain since the complex form of Fj(z;W). In this section, we conduct inferences of the test byp-value simulation using the bootstrap method. First, we select normal distributions and gamma distributions for the artificial data simulation. Then, we use the actual example of stocks to illustrate the validity of our test.

4.1 Bootstrap hypothesis tests

Assume that {X1,X2,…,XN} are independently and identically distributed samples fromF, and {Y1,Y2,…,YM} are independently and identically distributed samples fromG. Define the pooled samples as {X1,X2,…,XN;Y1,Y2,…,YM}. The detailed steps of the bootstrap approach are as follows:

In addition, about the selection of critical valuecj, we can use the quantile instead. Sorting theKtimes bootstrap samples from small to large, we get

4.2 Two sample normal distributions

Table 1. The dominance relationship of two normal distributions.

Figure 3.Estimation of distribution functions F (red line) and G (green line) under the density ratio model.

Figure 4.Estimation of functions F2(z;F) (red line) and F2(z;G) (green line) under the density ratio model.

Figure 5.Estimation of functions F3(z;F) (red line) and F3(z;G) (green line) under the density ratio model.

In the special case 1a, the two distributions are always the same, no matter what value ofj. For the remaining cases 1band 1c, we will infer the dominance relations based on the distribution plots, and then give the rejection rates of the tests. We take the case 1cas the example. First, we present the distribution function plots of 1cforFandGunder the density ratio model, as shown in Figure 3. From Figure 3 we can see that there is a crossover between the two distributions, so there is no first order stochastic dominance betweenFandG.Secondly, we want to judge whether there is second order stochastic dominance between the two distributions. We give the plots of

and

as shown in Figure 4. From Figure 4, we can see that the two functions still have intersecting parts.FandGshould not have second order stochastic dominance relationship.

Finally, we discuss whether there exists third order stochastic dominance. Figure 5 shows the plots of

and

From the figure, we find that there is a crossover between the two functions, so there is still no third order stochastic dominance relationship.

Now we give the rejection rates under different orders. EMP represents the test statistic under empirical distributions; DRM represents the test statistic under the density ratio model. The numbersj=1, 2, 3 in parentheses in the table indicate thejth order dominance. From Table 2, we can see that in the case of rejecting the null hypothesis, the rejection rates under the density ratio model are greater than those under empirical distributions. In the case of accepting the null hypothesis, the rejection rate should tend to 0, and the rejection rates under the density ratio model are smaller than those under empirical distributions. These all indicate that our test statistics under the density ratio model have better performance than the test statistic under empirical distributions.

4.3 Two sample gamma distributions

The DRM not only performs well in the case of common normal distributions, but also in the case of gamma distributions. We generate data from gamma distributions with the density function

f(x;α,β)=βαxα-1exp(-βx)/Γ(α),x>0,

whereαis the shape parameter andβis the scale parameter. For the same null and alternative hypothesises as Subsection 4.2, the sample sizes areN=M=200. Different from the normal distributions, the basis function for gamma distributions is chosen to beq(x)={1,x,log(x)}T. The numbers of repetitions areK=300 andB=500. The symbols in Table 3 have the same meanings as those in Table 1. Next, we take the case 2bas the example. It can be seen from Figure 6 that there is an intersection between the two distributions, and there is no phenomenon that one distribution is always above the other distribution. Hence, there is no first order stochastic dominance.

Table 2. Rejection rate of two normal distribution, α=0.05.

Table 3. The dominance relationship of two gamma distributions.

Figure 6. Estimation of distribution functions F (red line) and G (green line) under the density ratio model.

Figure 7. Estimation of functions F2(z;F) (red line) and F2(z;G) (green line) under the density ratio model.

Figure 8. Estimation of functions F3(z;F) (red line) and F3(z;G) (green line) under the density ratio model.

In Figure 7, there is a partial region at the left end, where the function F2(z;F) is above F2(z;G). Therefore, we can infer that there is no second order stochastic dominance between the two distributions.

Figure 8 shows that the plots of

and

still have an intersection area, so there is no third order stochastic dominant relationship.

From Table 4, we can see that the rejection rates under empirical distributions are very close to those under the density ratio model. However, when rejecting the null hypothesis, the rejection rates under the density ratio model are slightly larger; when accepting the null hypothesis, the rejection rates under the density ratio model are slightly smaller. This phenomenon shows that our test statistics under the density ratio model are relatively more effective than the test statistics under empirical distributions.

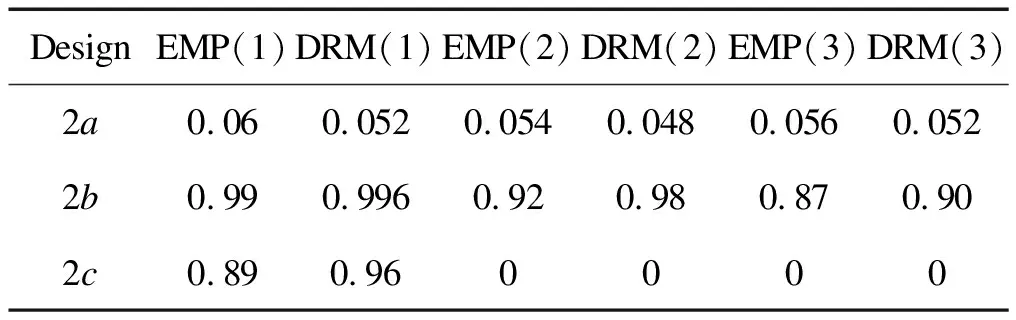
Table 4. Rejection rate of two gamma distribution, α=0.05.

Figure 9. Estimated distribution functions of DVN (dashed) and NOV (solid ) under the density ratio model.

Figure 10. Second order function estimates for DVN (dashed) and NOV (solid) under the density ratio model.

4.4 Real data example

Finally, we will apply our method to the real data example of stocks. In recent years, the topic of stocks has become more and more popular. Using the stochastic dominance method to compare the strength and weakness of two stocks is an effective method. We select two stocks from Devon Energy Corporation (DVN) and National Oilwell Varco (NOV) over the last three years (2017-2019) for analysis. The reason for choosing the two stocks is that their closing prices are not much different, and it is difficult to determine the pros and cons. We scale the data due to the large magnitude of the data in the likelihood estimation. The null hypothesis is taken as DVNNOV. Sample sizes areN=M=753, and the number of repetitions isK=300. The basis function of the density ratio model is selected asq(x)=(1,x,x2)T. Now, we give the distribution function plots of two stocks under the density ratio model.

From Figure 9, we can see that there is no first order stochastic dominance between the two stocks, but there may exist second order stochastic dominance. Next, we give the second order function plots of two stocks under the density ratio model.

It can be seen from Figure 10 that the second order function plot of DVN is always below that of NOV, which means that in the second order case, DVN dominates NOV. In addition, the value of the test statistic in second order case is -4.62× 10-4, which falls into the 95% confidence interval (-∞,4.17×10-2], and thep-value is 0.52. These all show that we cannot reject the null hypothesis, so we can infer that the stock DVN is second stochastic dominant the stock NOV. For risk averse people, we would recommend the stock DVN.

5 Conclusions

In this paper, we propose a semiparametric method to test high order stochastic dominance relations between two different populations. We introduce the test statistics based on the DRM and prove their asymptotic properties. A bootstrap method is developed to obtainp-values for making decisions. The normal distributions and gamma distributions are selected for artificial data simulation. Simulation studies show that our test statistic substantially improves the estimation efficiency compared to the test statistic based on empirical distributions. Finally, we apply our method to an actual example of stocks. A topic for further work is the extension of our method to test almost stochastic dominance relations. Another possible application of the current inference framework is to test factional stochastic dominance, for example, stochastic dominance of order 1+γ, for 0<γ<1, which is related to stochastic optimization.

Acknowledgments

The work is supported by the National Nature Science Foundation of China (Nos. 71971204, 71871208, 11701518), and the Provincial Natural Science Foundation of Anhui (No. 1908085MG236).

Conflictofinterest

The authors declare no conflict of interest.

Authorinformation

ZHOUYangis currently pursuing the master degree in Statistics and Finance with the School of Management, University of Science and Technology of China. His research interests include stochastic dominance and statistical test.

ZHUANGWeiwei(corresponding author) received the PhD degree in Probability and Statistics from the University of Science and Technology of China (USTC) in 2006. She is currently an Associate Professor with the Department of Statistics and Finance, USTC. Her research interests include statistical dependence, stochastic comparisons, semiparametric model, and their applications.