面向光学遥感影像的高效编码与重构

辛 蕾，李 峰*，鲁啸天，赵智祎，2，赵纪金

（1.中国空间技术研究院 钱学森空间技术实验室，北京 100094；2.北京信息科技大学 仪器科学与光电工程学院，北京 100192；3.北京市遥感信息研究所，北京 100192）

1 引言

卫星遥感是获取目标信息的重要技术手段，其获取的具备高空间、高时间、高光谱和高辐射分辨率“四高”特征的遥感图像数据，可为国防和民生提供信息和服务。随着空间遥感技术和数字成像技术的快速发展，大面阵高帧频探测器［1］已进入研制阶段，空间大面阵高帧频探测器获取的图像包含的信息量显著增加。海量高分辨率图像数据给有限的卫星存储容量和计算资源造成了巨大压力，同时对下行数据传统通道的实时传输能力形成考验。

为了减少传输和存储的数据量，星载数据处理分系统通常带有数据压缩模块，在星上进行压缩，在地面站进行解压缩。Beijng-1，ALOS，RapidEye 等卫星均采用基于离散余弦变换（DCT）图像压缩算法［2］，将空域信号变换到频域处理，对能量集中的少数系数进行量化编码达到压缩目的，但存在块效应，很难满足压缩比大于4的星上图像压缩；基于DWT 的压缩编码算法可以将变换后的能量大部分集中于低频系数，便于编码，如JPEG2000［3］，是遥感图像压缩比较理想的解决方案［4］，但存在的主要问题是计算量较大。无论是基于DCT 还是DWT 对图像进行编码，均需在探测器采样后进行，以减少采用过程中的冗余信息，因而如何将采样与压缩合二为一，减少资源浪费，也是研究者关注的领域。

在传统的信号处理领域，采样过程必须遵守香农采样定理，而当信号带宽较高时，需要更高的采样速率，使得采样与压缩处理成本显著增加。因而能够“突破”香农采样定理的压缩感知理论提供了一个全新的视角。压缩感知（Com⁃pressed Sensing，CS）［5］利用自然信号特有的稀疏性，采样冗余极少，在显著降低采样速率的同时重构出高质量的信号，已应用于医疗［6］、光谱分析［7］、成像［8］等领域。与传统信号处理方式相比，压缩感知方法将运算量从信号获取的编码端转移至解码端，采样数据量远远小于传统采样方法所获的数据量，并且能够抑制随机噪声，这在资源有限的遥感成像具有显著优势［9］及良好应用前景［10-11］。

本文借鉴压缩感知理论，根据大面阵相机所面临的数据采集与传输压力，提出一种光学遥感影像高效编码与重构方法，该方法利用多域联合感知矩阵获取多重压缩域信息，并基于该信息实现图像的快速重构。基于该方法设计了一套高效光学图像编码与重构系统，能够实现星上快速压缩和高保真的需求。

2 高效光学影像编码与重构系统工作原理

2.1 压缩感知理论

Candés 在2006 年从数学上证明了可以从部分傅里叶变换系数精确重构原始信号［12］，为压缩传感理论奠定了理论基础。Candés 和Donoho 在相关研究的基础上于2006 年正式提出了压缩传感的概念。其核心思想是将压缩与采样合并进行，首先采集信号的非自适应线性投影（测量值），然后根据相应重构算法由测量值重构原始信号。

根据调和分析理论，一个长度为N的一维离散时间信号f，可以表示为一组标准正交基的线性组合：

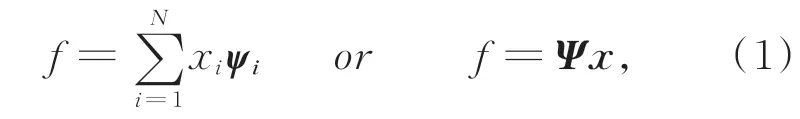
构造观测矩阵，测量过程可以表示为：

将（1）代入（2）可得：

其中：Φ为观测矩阵，为表示矩阵，观测矩阵Φ的列数远多于行数，这种数学表示即标准压缩感知框架。为确保现实环境中稀疏信号可重构的条件，需要感知矩阵满足约束等距特性。然而约束等距特性是为解决所有稀疏信号而推演出来的，事实上我们已知图像的一些固有特点，例如，非负性、平滑性等，所以在构建感知矩阵时严格遵守约束等距特性将严重限制该理论在图像压缩领域的实际应用。针对式（3），可以通过逆问题求解实现图像重构，即求解：

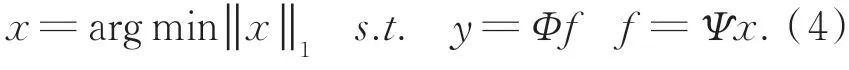
可以采用最优化方法对上式进行求解，如最小L1 范数法［13］、匹配追踪系列算法、迭代阈值法［14］等。

2.2 基于JPEG 的图像压缩方法

常用的JPEG 算法［15］将图像分为8×8 的块，在每个块上进行DCT 变换。DCT 变换为：

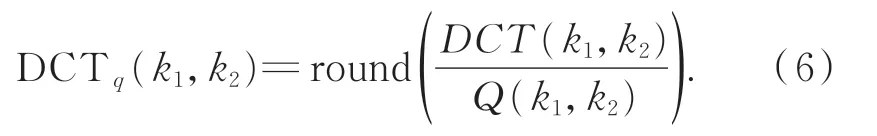
对量化后的矩阵进行霍夫曼编码，以完成压缩过程。解压缩过程即是上述过程的逆过程，即：

2.3 基于压缩采样的光学影像高效编码与重构方法

本文提出一种光学遥感影像高效编码与重构方法，在获取光学遥感影像同时进行高保真压缩，并实现快速重构。首先，突破约束等距特性构建利用硬件实现的多域联合感知矩阵，获取多重压缩域信息，然后，提出了一种基于Huber 函数的快速重构算法，能够实现图像高保真重构，重构效果优于传统JPEG 算法。该方法能够压缩采样一步完成，降低数据传输压力，实现信息高效编码和高保真重构。

2.3.1 多域联合感知矩阵构建

本文突破约束等距特性，充分利用成像探测器硬件内部构造，通过空域快速采样与压缩感知域变换结合实现多域信息的感知，以实现在数据快速压缩的同时提升数据特征丰富度。

多域联合感知矩阵Φ=RM×N包含两个子矩阵，同时获取压缩域与空域信息，即，其中，ΦD∈RM2为空域binning 下采样，可以最大程度的保留图像在空间域的边缘轮廓特征信息；ΦN∈RM1为经过压缩采样后得到的压缩感知域观测信息，M=M1+M2。在硬件设计上，将ΦN与ΦD的获取全部在探测器内部实现。

空域压缩利用探测器内部的binning 功能实现原始图像数据的下采样，即将相邻像元感应的电荷累加进行平均值求取，以提高灵敏度，减少数据量。公式为：

其中：Pi代指进行平均binning 步骤时像素点的周围像素点，n为像素点的个数，SAvr为所求平均binning 像素点像素值。

压缩感知观测值采用noiselet 变换［16］实现观测值数据的生成。noiselet 变换是一种将信号的全部能量分散到测量域的变换，且与Haar 小波变换满足不相关性，所以可以利用noiselet 域的随机下采样构建采样矩阵。noiselet 变换基函数的构成与小波变换基函数类似，都是由母函数进行多尺度迭代阈值收缩得到的。noiselet 的母函数χ（x）为：

利用母函数χ（x）进行迭代，在区间［0，1］的noiselet 基函数可以表示为：

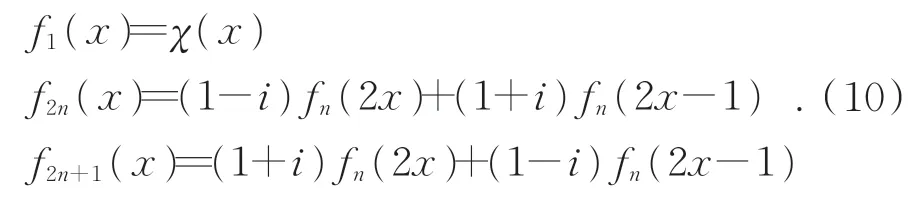
可以看出，利用上述迭代变换产生的noiselet变换矩阵中存在虚部，但是工程应用中虚部的实现比较困难，因此本文采用蝶形real-noiselet 变换，即一种不包含虚部，只包含实数的变换。变换方式采用如下步骤进行：

对于一个长度为n的向量x=[x1，x2，…，xn−1，xn]，使用图1 方法经过m步变换，最终得到的f=[f1，f2，…，fn−1，fn]中每一个元素都包含x中全部元素的信息，使得数据信号量全部分布在新生成数据元素当中，即原始信号通过real-noiselet 变换，其信号量被拆分到了各个观测值中。基于压缩感知原理，对经过realnoiselet 变换后的数据进行随机采样，实现数据压缩。

图1 Real-noiselet 变换过程Fig.1 Real-noiselet transformation process

2.3.2 基于Huber函数的高保真重构算法

基于多域联合感知矩阵对光学遥感影像进行压缩编码的过程可以描述为

其中：ΦN是real-noiselet 变换，ΦD是binning 下采样矩阵。需对原始影像f进行求解以得到重构影像。

本文提出一种基于Huber 函数的遥感影像重建算法，相比于迭代收缩阈值算法可以实现快速重构，且峰值信噪比（Peak-signal-noise-ratio，PSNR）和视觉效果更好。

Huber 函数表示为：

其中，α 为阈值。对于绝对值不大于α 的x，ρ(x，α)为二次曲线形式，对于绝对值大于α 的x，ρ(x，α)为线性形式。当α 取不同的值时，可以看到分段Huber 函数的曲线变化如图2 所示。根据Huber 函数的分段变换性质可知，随着梯度值增大，正则项对梯度值的惩罚力度由二次曲线变为线性曲线，因此，既有效地去除了高分辨率图像中可能出现高频噪声干扰，保证了重建图像的像素平滑性；同时，增大了对大梯度值的容忍度，使得图像中原有的边缘信息不会因为正则项而模糊掉。Huber 函数将L1 与L2 范数进行结合，使得Huber 函数即具备抗噪性，又具备稳定性，在噪声的影响下也能得到较好的反演结果。

图2 不同参数下的Huber 函数曲线Fig.2 Huber function curve under different parameters

引入以Huber 函数为目标函数的图像先验概率分布为：

其中，D表示高分辨率图像z的一阶导数的近似计算，即在高分辨率图像z中的每一个像素点位置上，分别在水平方向、垂直方向以及两个互相垂直的对角方向上计算一阶差分的二范数，以此来代表图像的一阶导数。在当前正则项下，可推导出目标函数及其导数的表达式为：

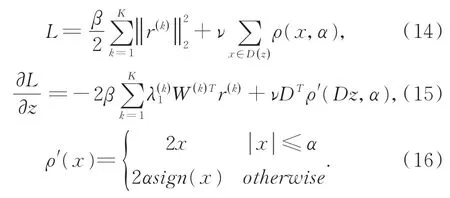
公式（16）为分段Huber 函数的一阶导数形式。此时，残差项和正则项均满足凸函数性质，所以可以通过梯度下降算法迭代求解上式。

3 结果与讨论

3.1 仿真实验结果

为了验证算法有效性，本文选择了四组影像进行仿真实验，如图3 所示，分别为标准影像Le⁃na，吉林一号影像，以及以单一目标红外影像［17］和场景红外影像［17］。

图3 原始影像Fig.3 Original images

基于本文所提出的光学遥感影像高效编码与重构方法，对上述影像进行多域感知编码，获得4 倍压缩数据，其中binning 下采样率为原始影像的1/16，其余数据均为压缩感知域数据，采用基于Huber 函数的重构算法对原始影像进行重构，结果如图4 所示。

图4 基于多域联合感知压缩数据的重构图像Fig.4 Reconstructed images based on multi-domain joint sensing compressed data

本文采用峰值信噪比（PSNR）和结构相似性（structural similarity，SSIM）作为评价指标，定量化评价重构效果。PSNR 定义为：

其中：x是原始影像，xR是重构后的影像，N2是影像包含的像素个数，p是灰度影像的最大像素值。PSNR 是最普通和使用最为广泛的图像客观评价指标，是基于误差敏感的图像质量评价。考虑到人眼的视觉特性，PSNR 作为单一指标经常会出现评价结果与人的主观效果不一致的情况，因而增加结构相似性作为图像质量评价指标。SSIM 定义为：

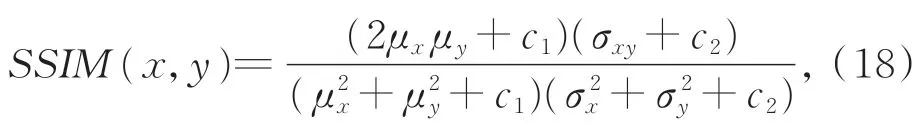
其中：μx，μy分别为x和y的平均值；σx，σy分别为x和y的标准差；σxy表示x和y的相关性；c1和c2是为避免分母为0 的常数。在4 倍压缩情况下，本文所提出的方法与JPEG 方法进行比对，两种方法分别得到的结果如表1 所示。由表1 可知，本文所提出的图像压缩编码方法重构结果优于JPEG 方法。

表1 重构效果对比（4 倍压缩）Tab.1 Comparison of reconstruction results（Compres⁃sion ratio=4）

为了进一步评价本文所提出的图像压缩编码与重构方法的性能，针对8 倍压缩比的情况作了实验验证，重构效果如表2 所示。由表2 可知，随着压缩比的增大，本文所提出的方法与JPEG方法的效果均有所下降，但本文的方法仍优于JPEG 方法。值得注意的是，在本文所提出方法的基础上，可以采用哈夫曼编码进一步降低信息熵冗余，因而为了更好的说明本文提出的方法可以达到的压缩比和重建效果，作为对比的JPEG算法也没有采用哈夫曼编码。

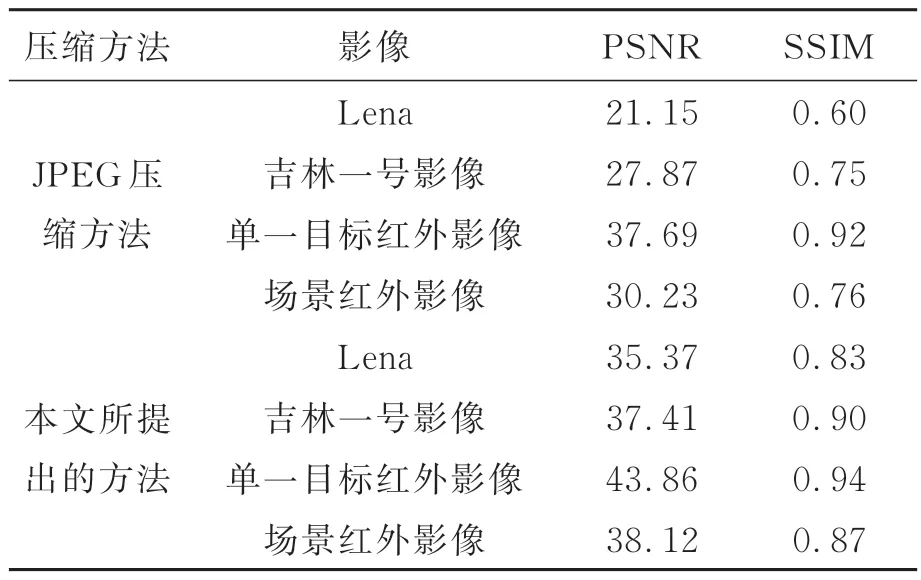
表2 重构效果对比（8 倍压缩）Tab.2 Comparison of reconstruction results（Compres⁃sion ratio=8）

3.2 高效光学图像编码与重构系统

为了验证基于多域感知的图像压缩与重构方法的可行性，本文搭建了相应的基于多域感知的高效光学图像编码与重构系统，如图5 和图6所示。

图5 高效光学图像编码与重构系统Fig.5 System of high-efficiency optical image coding and reconstruction

图6 高效光学图像编码与重构系统结构图Fig.6 Structure diagram of high-efficiency optical image coding and reconstruction system

系统采用Xilinx Spartan6 系列XC6SLX45 作为核心处理器，具有43 661 个逻辑单元，时钟单 元CMT 为4，Block RAM 为2 088 Kb，采 用1000 M 以太网RJ-45 接口用做数据交换。

本文利用上位机实时显示binning 下采样数据，同时获得binning 下采样数据和noiselet 感知数据存入存储空间，按需对影像进行快速重构。图7 为不同压缩倍率下数据的传输速率，由于相机的读取速率一定，因而当固定时间内传输的数据量减少时（压缩倍数增大），以太网口的传输速率降低，表明图像得到了压缩。

图7 上位机速率变化示意图Fig.7 Schematic diagram of host computer rate change

4 结论

本文根据大面阵相机所面临的数据采集与传输压力，借鉴压缩感知理论，提出一种光学遥感影像高效编码与重构方法，该方法利用多域联合感知矩阵获取多重压缩域信息，并基于该信息实现图像的快速重构。实验结果证明：本文所提出的光学图像编码与重构方法，PSNR 和SSIM均优于JPEG 压缩方法，针对吉林一号、单一目标红外影像、场景红外影像，在4 倍压缩前提下，PSNR 达到40 dB，SSIM 优于0.8。本文基于该方法设计了一套高效光学图像编码与重构系统，能够实现星上快速压缩和高保真重构的需求。