面向在轨装配的冗余索并联机构变刚度控制

于金山，李 潇，王国星，陶建国*，王浩威

（1.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001；2.北京空间飞行器总体设计部，北京 100094；3.北京卫星制造厂有限公司，北京 100094）

1 引言

随着航天技术的发展，航天器的结构尺寸越来越大。很多大型航天器如空间天线、大型SAR卫星等，其结构尺寸超出了运载火箭的装载体积。因此，大型空间结构需要采用在轨装配的方式［1］。按照有无人直接参与，在轨装配可分为有人在轨装配和无人在轨装配两种类型［2］。有人在轨装配是指由航天员操纵工具直接进行在轨装配作业，在此过程中航天员身体会暴露在恶劣的空间环境中，因此该方式具有很大的危险性。无人在轨装配是指借助空间机器人或机械臂采用遥操作或自主操作的方式进行在轨装配作业。该方式具有很高的安全性，可以满足长期工作要求，因此成为了在轨装配的主要方式。

目前，空间在轨装配操作任务所采用的机械臂多为杆支撑串联机械臂［3］。这种机械臂的特点是控制方便；但是当关节数量较多时质量会极大地增加，提高了系统能耗，此外，当臂杆较长时机械臂的刚度会降低，因此难以满足大跨度、高精度的在轨装配需求。相对于杆支撑串联机构，索并联机构结合了绳索驱动的优势和并联机构［4-5］的特性，具有结构简单、易于构建、质量轻、工作空间大以及承载能力强的特点［6］，广泛应用在起重［7］、天文观测［8］及飞行器风洞试验［9］等领域。由于具有这些特点，索并联机构在空间在轨装配领域具有良好的应用前景。

索并联机构的刚度是影响其工作性能的一项重要指标，它在提高系统稳定性以及降低系统振动方面扮演着重要角色。绳索作为柔性体具有弹性，这不可避免地对系统的刚度产生了消极的影响，尤其是在绳索较长的情况下。这种影响造成机构定位精度下降。然而，较低的刚度能提高机构的柔顺性，这对于一些接触性作业是有利的。Verhoeven 等研究了索并联机构的工作空间、刚度和奇异性，并通过仿真分析了不同位置处机构的刚度，但在研究过程中忽略了绳索拉力对机构刚度的影响［10］。事实上，由于应力刚化原理［11］，绳索拉力对索并联机构的刚度具有重要影响。王克义等对一种索牵引康复机器人进行了研究，在运动学和动力学方程的基础上，通过仿真分析了绳索弹性对机器人运动控制的非线性影响，但在绳索弹性对机器人影响机理方面缺乏更为深入的研究［12］。隋春平等根据微分变换原理对一种3 自由度索驱动并联操作臂的刚度进行了分析，发现操作臂的刚度与绳索拉力有关，在此基础上通过位置和张力混合控制策略对操作臂进行了刚度控制［13］。但该方法只针对具有一个冗余度的四索三自由度并联机构，对于更多冗余度的索并联机构的刚度控制有待进一步的研究。Behzadipour 等首先建立了单根绳索的刚度模型，然后进一步建立了多根绳索组成的索并联机构的刚度模型［14］。该研究在建立索并联机构完整刚度模型的基础上，重点研究了机构稳定性与刚度模型的关系，却未对机构的变刚度问题进行深入研究。刘欣等基于微分变换和线几何理论，建立了包含关节弹性变形以及绳索张力等因素的索并联机器人刚度模型，通过大射电望远镜5 m 缩尺模型进行了实验验证［15］，但未在该模型的基础上进行刚度控制方面的研究。Yeo 等研究了索并联机构的变刚度特性，考虑到在绳索张力范围较小的情况下，通过改变绳索张力难以使机构刚度产生有效的变化，因此设计了一种由扭矩弹簧组成的变刚度机构，但该机构的引入增加了系统设计和控制的复杂性［16］。Jamshidifar 等设计了一种冗余运动学约束的索并联机构，对冗余绳索张力对机构刚度的影响进行了研究，并且以期望方向的刚度最大化为目标对机构进行了刚度控制［17］，但在控制过程中只考虑了绳索拉力约束，未进一步考虑避免外界扰动力导致绳索过度张紧或松弛的安全边界。Nelson 提出了一种提高索并联机构刚度的方法，即将绳索与运动平台铰接点变为滑轮，绳索穿过该滑轮后再与支架固连，这种方法可以使实际绳索数量增加为原来的一倍，显著提高了机构的刚度［18］，但该方法增加了滑轮的数量，一定程度上也增加了绳索的数量，提高了系统的复杂性，还会导致机构的工作空间有所减小。Picard 等提出了一种面向刚度的索并联机构张力分布算法，用来降低运动平台因外力干扰导致的位移，通过仿真和实验验证了算法的有效性［19］，但该研究只考虑了机构某单一方向（侧向）的刚度，未能建立考虑多个方向刚度的张力分布算法，在应用中具有一定的局限性。

以上研究中，有些对影响索并联机构刚度的因素考虑不全面，所建立的刚度模型不完整，从而限制了它在控制中的应用；有些改变机构刚度的策略只能应用于某一种特定构型的机构，局限性很大；还有一些研究提出了用来改变机构刚度的设计方案，但增加了机构元件的数量，提高了系统的复杂性。本文针对大型空间结构的在轨装配任务，提出了大跨度索并联机构方案，即通过驱动多根绳索牵引执行器进行在轨装配作业。针对该冗余索并联机构的刚度展开研究，为了提高它在不同工况下的工作性能，提出了一种变刚度控制算法，该算法无需增加元件，通过直接调节绳索张力的方式使期望方向的刚度达到理想要求；同时考虑机构不同方向的刚度，通过分配权重的方式对多个方向的刚度进行不同优先级的控制。仿真与实验验证了该变刚度控制算法的性能，尤其在改变索并联机构薄弱方向的刚度方面具有良好的效果。本文所提的变刚度控制算法也可应用于不同类型的冗余索并联机构中。

2 机构描述及刚度模型建立

2.1 机构描述

图1 为面向在轨装配的索并联机构示意图，它主要由框架、驱动单元、绳索以及运动平台组成。驱动单元包含电机、减速器及滑轮等元件，通过驱动绳索牵引运动平台实现大范围的运动。运动平台上面安装有各种适配器［20］，用于执行在轨装配过程中的夹持、旋拧等操作。

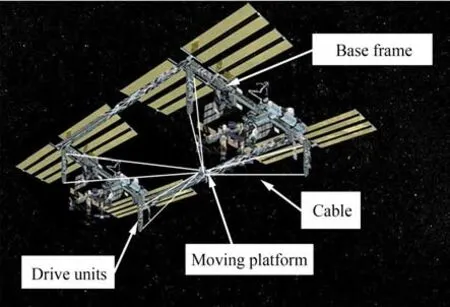
图1 面向在轨装配的索并联机构示意图Fig.1 Schematic diagram of cable-driven parallel mecha⁃nism for on-rail assembly

本文所设计的索并联机构预期安装空间为一长方体区域，运动平台形状为长方体，其几何参数如表1 所示。由于绳索具有单向受力性，因此索并联机构必须采用冗余驱动的方式，即绳索数量必须大于运动平台的自由度数，从而实现对运动平台的完全约束［21］。在轨装配作业中，运动平台需要实现空间内6 个自由度的运动。为了满足机构约束要求，同时使布局具有对称性，选取绳索数量为8，其构型如图2 所示。

图2 索并联机构构型示意图Fig.2 Schematic diagram of cable-driven parallel mecha⁃nism configuration

表1 索并联机构几何参数Tab.1 Geometric parameters of cable-driven parallel mechanism

该构型采用绳索上下交叉布局的方式，即顶部的4 个出绳点通过绳索与运动平台底部的4 个顶点相连，底部的4 个出绳点与运动平台上部相连。为了避免绳索发生干涉，运动平台上部的4个绳索连接点并不位于顶点位置，而是向中间移动一段距离。这种构型可以使机构具有更大的承载能力，同时可以使运动平台实现更大的倾转角度［22］。

在空间环境中，绳索不会产生由于重力作用导致的悬链线变形，因此可以直接建立为直线模型。图2 中，O-XYZ为全局坐标系，P-xyz为局部坐标系。Bi和Pi（i=1，2，...，8）分别表示绳索出线点和运动平台连接点。Obi为出绳点在全局坐标系中的位置矢量，O p为局部坐标系原点在全局坐标系中的位置矢量，pi为绳索与运动平台连接点在局部坐标系中的位置矢量，ORP为局部坐标系到全局坐标系的旋转矩阵。

单位绳索矢量可表示为：

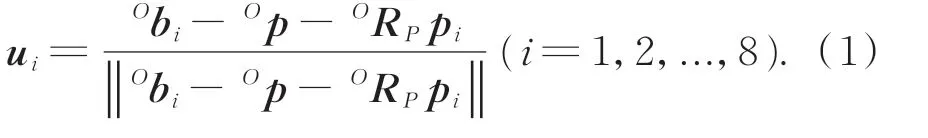
令ti=tiui(i=1，2，...，8)为绳索拉力矢量，ti为绳索拉力值，fp为运动平台所受外力，τp为运动平台所受外力矩。由力平衡条件可得：

式（2）和式（3）合并得到：

2.2 刚度矩阵

当作用在运动平台上一个微小外力旋量dF时，运动平台会产生一个微小位姿变化dX，因此索并联机构的刚度可表示为：

式中K为索并联机构的刚度矩阵。把式（4）代入式（5），得：

可以看到索并联机构的刚度矩阵由两部分组成，将这两部分分别设为K1和K2。对K1进行计算得到：

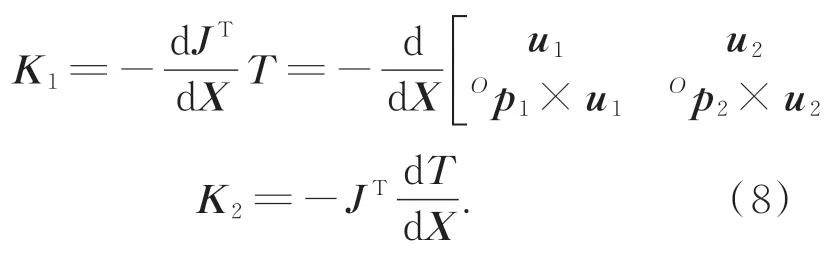
索并联机构的雅可比矩阵为：

式中：L为绳索长度矩阵，L=[l1l2...l8]T。J与索并联机构的结构矩阵互为转置。

把式（9）代入式（8），得：

令ki为绳索i的刚度，则：

式中：Ei为绳索i的弹性模量，Ai为绳索i的截面面积，loi为绳索i的初始长度。则式（10）中：

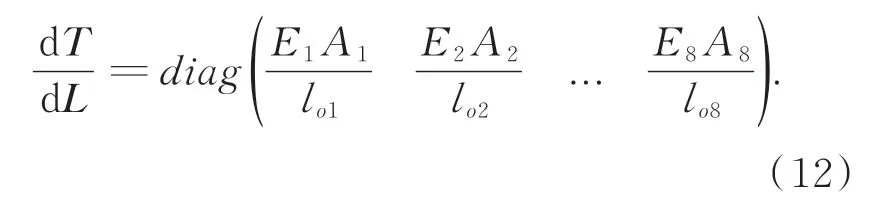
把式（12）代入式（10），得到：

于是得到索并联机构的完整刚度矩阵：

3 索并联机构变刚度控制策略

由式（14）可以看出，索并联机构的刚度不仅与绳索刚度有关，还与绳索张力有关，因此，与绳索刚度有关的K2称为被动刚度，与绳索张力有关的K1称为主动刚度［15］。在索并联机构位姿确定的情况下，通过调节绳索张力可以改变索并联机构的刚度，实现机构的变刚度控制。对式（4）进行求解，得：

式中：JT+为JT的Moore-Penrose 逆，JT+F为式（4）的特解。N=nul（lJT）为结构矩阵JT的零空间，N∈R8×2，λ=[λ1λ2]T为任意矢量。Nλ为式（4）的齐次（零空间）解，其表现为索并联机构的内力，对运动平台整体不产生力作用。由于绳索只能受拉而不能受压，因此绳索张力必须大于零。而在求解过程中，并不能保证特解JT+F的所有元素为正，这会违反绳索张力大于零的要求，因此可以通过设置任意矢量λ的值来调节齐次解部分，使整体绳索拉力大于零。

在实际应用过程中，为了避免绳索发生虚牵，索并联机构的绳索拉力应高于一个最小值-t。此外，受驱动器最大驱动力矩以及绳索许用拉力（与绳索抗拉强度、绳索横截面积等有关）的限制，绳索拉力存在上限值-t。因此，绳索拉力的约束条件为：

于是，求解索并联机构绳索拉力矩阵T的问题可以简化为求解λ，使之满足绳索拉力约束条件式（16）。令满足约束条件的矢量λ的集合为Λ，其在二维空间内呈现为多边形，如图3所示。

图3 矢量λ 集合Λ 的可行多边形Fig.3 Feasible polygon of λ set Λ

综上，当索并联机构的位姿确定时，在满足绳索拉力约束条件的情况下，通过调节任意矢量λ可以改变绳索的拉力分布，从而实现对机构的变刚度控制。

刚度矩阵中的主对角线元素分别为机构沿x，y，z轴的平动刚度Kx，Ky，Kz以及绕各轴的旋转刚度Kα，Kβ，Kγ，非对角线元素为不同方向的耦合刚度，如下：

由于非对角线元素相对整个刚度矩阵的影响很小，因此在研究中通常只针对主对角线元素进行分析。以运动平台位姿X=［00 12.5000］T为例，设置绳索拉力下限值-t和上限值-t分别为100 N 和2 000 N，绳索采用直径为2 mm 的Dyneema 绳。当运动平台所受外力为0 时，计算得到不同绳索拉力分布对索并联机构刚度的影响，如表2 所示。

由表2 可以看出，主动刚度K1与被动刚度K2相比较小。以绳索张力约为100 N 时为例，索并联机构由主动刚度K1产生的3 个平动方向的刚度（K1（1，1），K1（2，2），K1（3，3））远小于被动刚度K2的3个平动方向刚度（K2（1，1），K2（2，2），K2（3，3））。随着索并联机构张力的增加，主动刚度K1的值显著增大，但与被动刚度K2相比仍然具有很大差距。因此，在被动刚度较大的情况下，通过改变绳索张力的方式调整机构整体刚度不会产生明显的效果。值得注意的是，在被动刚度较小的方向（绕z轴的旋转刚度Kγ），通过增大绳索拉力可以显著提高该方向的刚度。在绳索拉力约为100 N 时，绕z轴的旋转刚度Kγ=1 714 N/rad；当绳索张力增加到约1 000 N 和2 000N 时，该方向的旋转刚度分别达到7 130 N/rad 和13 200 N/rad，因此，在索并联机构刚度较低的方向，通过改变绳索张力的方式可以取得良好的变刚度效果。此外，非主对角线元素位置的耦合刚度相对极小，对整体刚度的影响可以忽略。

表2 不同绳索拉力分布对索并联机构刚度的影响Tab.2 Influence of different tension distribution on stiffness of cable-driven parallel mechanism

进一步分析矢量λ变化对旋转刚度Kγ的影响，如图4 所示。可以发现，随矢量λ的变化，旋转刚度Kγ变化显著，且刚度极值发生在绳索约束条件的极限部分。

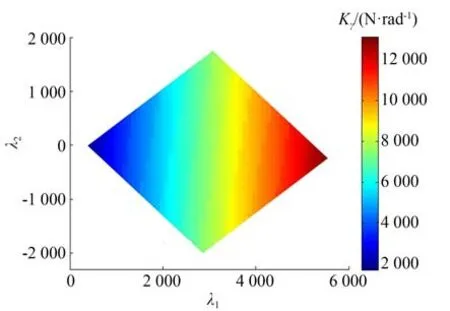
图4 矢量λ 变化对Kγ 的影响Fig.4 Influence of λ on Kγ

考虑到在矢量λ集合Λ 的可行多边形边界位置处，绳索拉力处于约束条件的极限值，此时在有外力扰动的情况下，绳索会发生过度张紧或松弛，使得绳索拉力超出约束条件的边界值，导致系统失效或破坏。为了避免这种情况，定义了可行多边形的安全边界［19］，如图5 所示。图中，λBC为可行多边形的质心，λM和λSM分别是可行多边形边界和安全边界上的点，且为介于(0，1)之间的系数，用于限定安全边界所包含区域的范围。

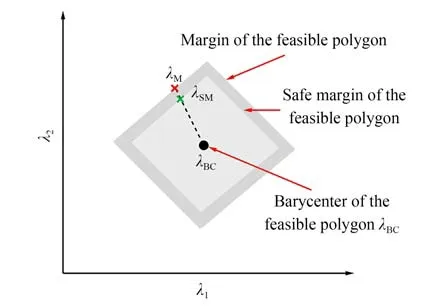
图5 矢量λ 可行多边形安全边界Fig.5 Safe margin of feasible polygon of λ set

为提高计算效率，消除刚度矩阵中对整体影响极小的耦合项，只保留主对角线元素，将它改写为矢量形式：

期望刚度为：

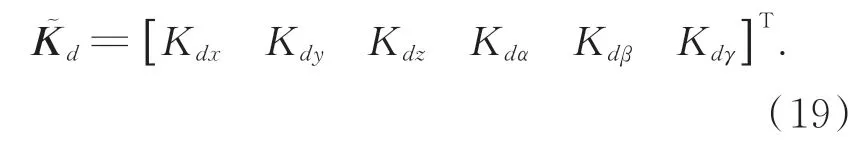
期望刚度与实际刚度的差值为：

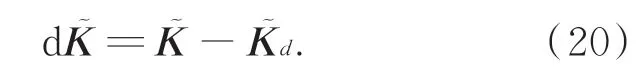
于是索并联机构的变刚度控制可转化为优化问题（见式（21）），即在满足安全边界条件的情况下，通过调节矢量λ来改变绳索张力，从而使实际刚度最大程度接近期望刚度。

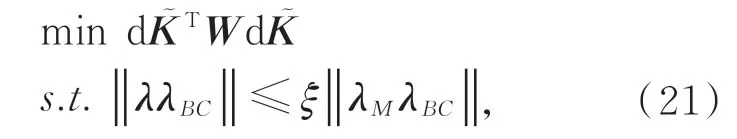
式中 ：W为权重对角矩阵，W=由于使索并联机构所有方向的刚度均达到期望刚度值是不可能也是不必要的，因此，可以通过分配权重的方式使机构某个方向的刚度优先被控制，从而达到理想的变刚度效果。该优化问题的求解算法流程如图6 所示。

图6 求解优化问题算法的流程Fig.6 Flow chart of algorithm for solving optimization problems

4 仿真与实验

4.1 ADAMS 仿真

以运动平台搭载适配器进行旋拧操作为例，如图7 所示。操作时，运动平台需要承受z向的扰动力fp和扰动力矩τp，因此要求机构在这两个方向上具有较强的刚度。设在位姿X=［0012.5000］T处，z方向平动刚度的期望值Kdz=8 000 N/m，转动刚度期望值Kdγ=12 000 N/rad。由表2 知z方向的平动刚度较大，且绳索拉力分布对其影响不明显，因此只考虑z方向旋转刚度的控制，取权重对角矩阵W的元素w66=1，其余元素为0，安全边界系数ξ设为0.8，则通过变刚度控制算法计算得出绳索张力分布为：

图7 旋拧操作时运动平台受力Fig.7 Force diagram of moving platform during screwing operation

此时Kz=9 309 N/m，Kγ=10 091 N/rad。由于受安全边界限制，为了避免绳索张力在扰动力的作用下超出约束条件，转动刚度值Kγ未能达到期望值，而在安全边界处达到最大值。

在ADAMS 环境下采用绳索模块建立索并联机构的模型，如图8 所示。对8 根绳索分别施加由变刚度控制算法得出的拉力分布值，在运动平台上施加微小载荷，求解载荷方向的变形量，从而测量索并联机构的实际刚度，计算结果与理论结果如表3 所示。

图8 ADAMS 中索并联机构的模型Fig.8 Model of cable-driven parallel mechanism in AD⁃AMS

表3 索并联机构刚度的理论值与测量值比较Tab.3 Comparison of theoretical and measured stiffness of cable-driven parallel mechanism

对比刚度的测量值与理论值，发现测量值相对理论值较小，这是由于在ADAMS 环境中建模时，为了使绳索可以绕过滑轮，对绳索进行了一定程度的延长，从而降低了机构的刚度。此外，引入滑轮使得出线点的实际位置相对理论位置发生了较小的变化，带来了一定的误差。整体来看，测量值与理论值的误差不大，验证了刚度模型的正确性。

在该模型的基础上，进一步验证变刚度控制的性能。在运动平台的z方向施加扰动力fpz（t）和扰动力矩τpz（t）如下：

分别对8 根绳索施加采用本文提出的变刚度控制算法求解出的绳索张力以及未考虑变刚度的质心法（即λ取值为可行多边形质心λBC［23］）求解出的绳索张力，分析施加上述扰动时运动平台的振动情况，结果如图9 所示。

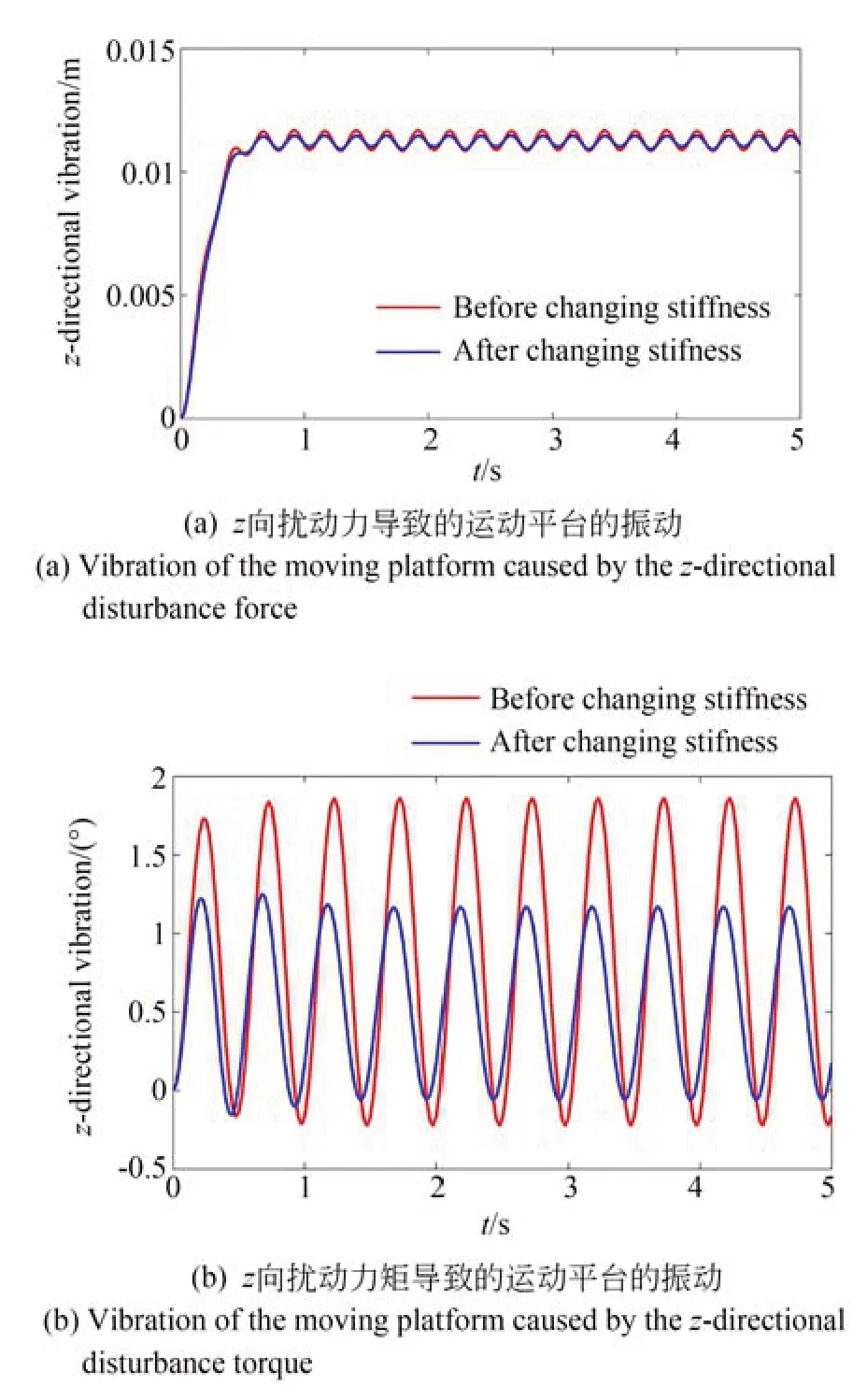
图9 扰动力和力矩导致的运动平台的振动Fig.9 Vibration of moving platform caused by distur⁃bance force and torque respectively

由图9（a）可以看出，两种不同求解方法求解得到的绳索张力在抵抗z向扰动力方面的作用没有明显区别。这是由于本文所研究的索并联机构在z向具有较强的被动刚度，因此在该方向上，由绳索张力产生的主动刚度对整体刚度无显著影响。而对于z向转动刚度，由于该方向的被动刚度较弱，因此通过改变绳索张力的方法可以明显改善整体刚度。由图9（b）可以看出，对绳索施加由未考虑刚度的绳索张力分布算法得出的绳索张力时，运动平台在扰动力矩的作用下产生较强的振动。而在该方向设定较强的期望刚度时，对绳索施加通过变刚度控制算法得出的绳索张力后，运动平台的振幅明显减弱，由2°降为1.3°，振动降低了35%。因此，本文提出的变刚度控制算法可以有效改变索并联机构薄弱方向的刚度，使该方向的刚度满足期望要求，从而极大地改善系统的性能。

4.2 样机实验

本文所提出的索并联机构变刚度控制算法不只适用于冗余度为2 的索并联机构，也可适用于冗余度为1 或更高冗余度的索并联机构。其区别在于当冗余度为1 时，λ可行多边形降维成一条线段，而对于冗余度较高的索并联机构，λ可行多边形转化为空间三维多面体或更高维度的超多面体，其安全边界也会相应发生变化。本文在已有的一种四索并联机构样机（图10）的基础上，对变刚度控制算法的性能进行了实验验证。该四索并联机构由4 台伺服电机驱动卷轴转动，进而带动绳索牵引运动平台进行运动。每根绳索一端与卷轴连接，另一端绕过拉力传感器与运动平台相连。拉力传感器可以对绳索拉力进行实时测量，用于样机的力反馈过程。样机的相关参数如表4 所示。

图10 四索并联机构样机Fig.10 Prototype of four-cable driven parallel mechanism

表4 四索并联机构样机参数Tab.4 Prototype parameters of four-cable parallel mecha⁃nism （mm）

该索并联机构在竖直方向上（z向）的被动刚度为0，因此，可以通过控制绳索拉力的方式提高其z向的主动刚度，从而提高该方向的整体刚度。以运动平台处于中心位置为例，设置绳索拉力为[10，300]N，只考虑z向刚度，取权重对角矩阵W的元素w33=1，其余元素为0，安全边界系数ξ设为0.9，通过变刚度控制算法使其z向理论刚度值分别达到800 N/m 和1 000 N/m。将运动平台悬空放置，在z向施加一系列不同大小的力，测量其微小位移量，计算得出实际刚度。实验结果如图11 所示。

从图11 可以看出，四索并联机构样机在z方向的刚度测量值小于理论值，这是因为每根绳索的实际长度大于理论长度。此外，卷轴受力后也产生了一定的变形量，这也是造成样机刚度测量值降低的一个重要因素［19］。两种情况下刚度测量值的相对理论值误差分别为16.3% 和14.6%，结合文献［19］，该误差在可接受的范围内。

图11 四索并联机构刚度测量结果Fig.11 Measurement results of stiffness of four-cable driven parallel machenism

5 结论

本文对一种面向在轨装配的冗余索并联机构的刚度进行了分析，建立了其完整刚度模型。其次，分析了绳索张力分布对不同方向刚度的影响。然后，考虑影响绳索张力分布的矢量λ的安全边界，建立了索并联机构的变刚度控制算法，该算法消除了刚度模型中对整体影响较小的耦合刚度，提高了计算效率，并且可以通过分配权重的方式对不同方向的刚度进行不同优先级的控制。最后，以旋拧操作为例进行仿真，结果表明：在对运动平台施加扰动力时，相较于未考虑变刚度的索力分布，采用变刚度控制算法求解出的索力分布可以使薄弱方向的振动降低35%。样机实验结果表明，在对索并联机构样机进行刚度控制后，刚度的测量值与理论值具有较强的拟合性，误差分别为16.3%和14.6%。本文的变刚度控制方法可以有效改变索并联机构薄弱方向的刚度，使其达到预期刚度值。这对于提高系统的性能具有重要意义。