CVOFLS 方法在多涡剪切流场问题中的应用

崔立营 杨英歌

（1.西安欧亚学院，陕西 西安 710065； 2.西安北方光电股份有限公司，陕西 西安 710043）

现实生活中很多现象与运动界面密切相关，如水滴下落、气体爆炸等问题[1]，因此，研究运动界面的数值模拟具有深远意义。在欧拉方法中，Level Set 方法[2]和VOF 方法[3]因其内存占用小，易解决结构复杂的流体运动界面问题以及实现简单等优点而被广泛采用。基于此，有学者提出了耦合两类方法优点的CLSVOF 方法。

孙东亮等[4]于2010 年给出了一种新的CLSVOF方法，该方法虽然简化了原始的CLSVOF 方法，但其方法理论以及重构界面的过程比较复杂。李强等[5]于2011 年创造了一种全新的CLSVOF 方法。该方法自带质量校正公式，并且计算自由运动界面精度很好，但其计算效率不高。

Level Set 方法在模拟运动界面方面会计算得到更为准确界面法向和曲率,又考虑到VOF 方法具有计算效率高以及质量守恒性好的优点和界面法向与曲率较差的缺点；因此,若将Level Set 方法耦合到VOF 方法中，便可克服其缺陷。本文采用了耦合Level Set 与VOF 的新方法─CVOFLS 方法[6]，并通过对多涡剪切流场问题的模拟，验证了CVOFLS 方法效率更高,界面守恒性更好。

1 输运方程

CVOFLS方法是一种新的耦合VOF与Level Set方法。运动介质的速度场为u(u,v)，Level Set 函数φ(X,t)以及VOF 函数F(X,t)所满足的输运方程表达式分别如下：

CVOFLS 方法中采用周文等[7]的数值方法对方程（1）和（2）进行离散。

Level Set 函数的运算过程中需对函数φ(X,t)进行重新初始化，进而获得新的点X 到界面 Γ (t)的符号距离函数；该方法可以保证Level Set 函数的数值稳定性，并使得其在求解域内具有优良的光滑性。

对方程（3）进行离散得到的稳态解来重新初始化符号距离函数。其中τ是伪时间，使用sign(φ0)=近似计算sign(φ0)，∆x、∆y为离散坐标下的x 轴与y 轴的空间步长。

2 数值方法

2.1 VOF 输运方程的离散

为了计算方便，方程（2）可写为守恒形式：

Sussman 和Puckett[8]提出用通量分裂算法来求解方程（4），其离散形式如下：

2.2 Level Set 输运及重新初始化方程的离散

2.2.1 空间离散

方程（1）和方程（3）同属于Hamilton-Jacobi 型方程。

其中Level Set 函数方程（1）可写为：

Jiang和Peng[9]专门针对Hamilton-Jacobi型方程求解，给出了经典的五阶WENO（Weighted Essentially Non-Os cillatory）格式。故本文空间离散采用该格式，进而可得该方程的离散形式[10]：

2.2.2 时间项离散

采用三阶TVD-R-K(Total Variation Diminishing Runge-Kutta)格式对方程（1）、（3）进行离散，可以有效避免数值振荡，其表达式为：

3 数值算例

为了验证本文提出的CVOFLS 方法的有效性，下面以模拟多涡剪切流场的界面运动为例，检验CVOFLS方法的模拟效果，即考察圆心在（0.5，0.5）、半径为0.15 的圆在速度场中的运动情况，整个流场计算区域为[0,1]×[0,1]，时间步长为0.002s。

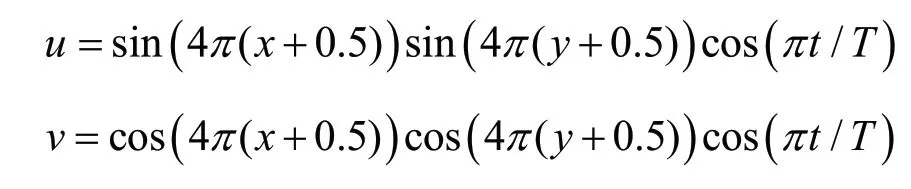
其中t 为模拟时间，T 为多涡剪切流场的周期。

图1、图2 分别给出了周期T=1s 和T=2s 时采用CVOFLS方法模拟多涡剪切流场的数值结果。由图可知，CVOFLS 方法在T=1s 时模拟的数值结果与初始时刻的结果基本重合，表明其具有很好的稳定性及守恒性。而在T=2s 时模拟的数值结果效果良好，具有较好的守恒性。

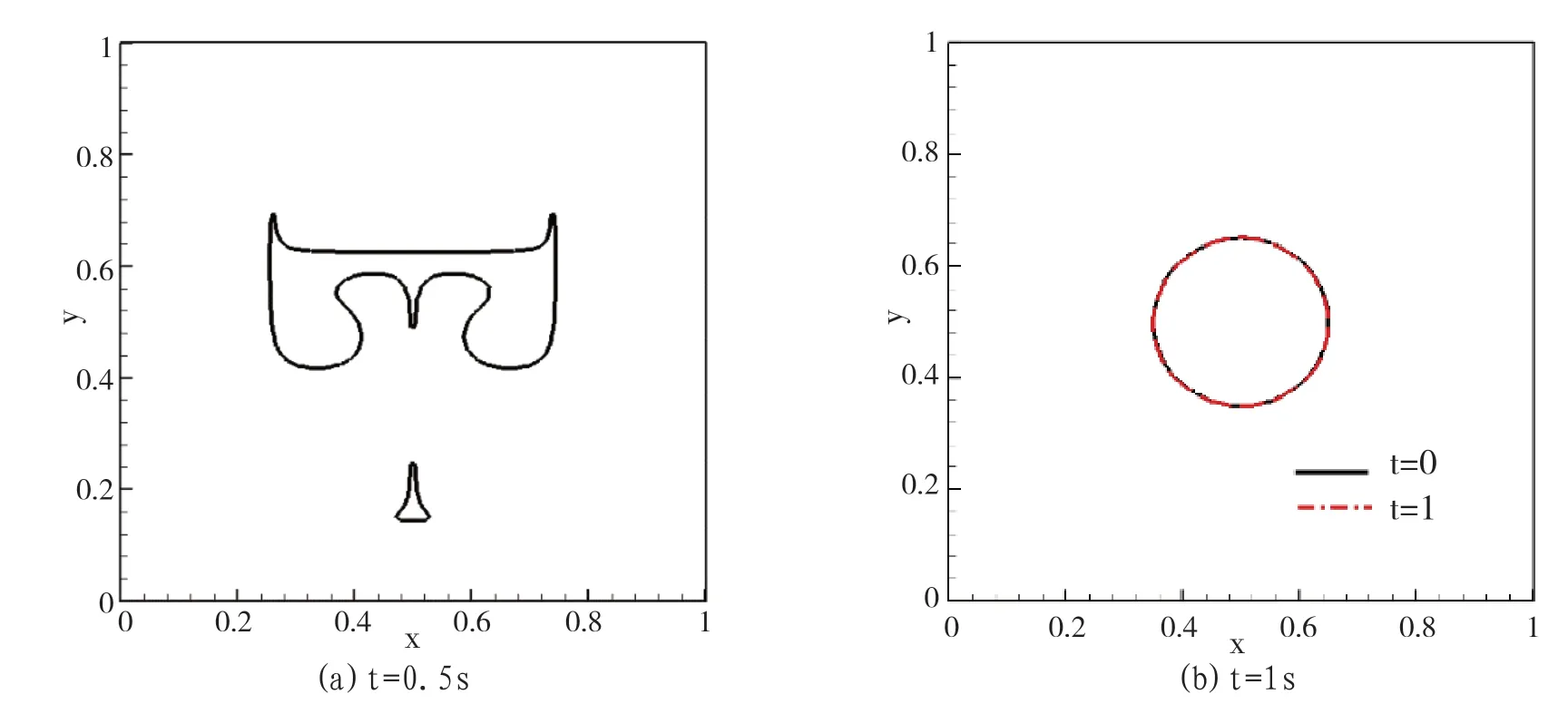
图1 多涡剪切流场的模拟结果(T=1s)

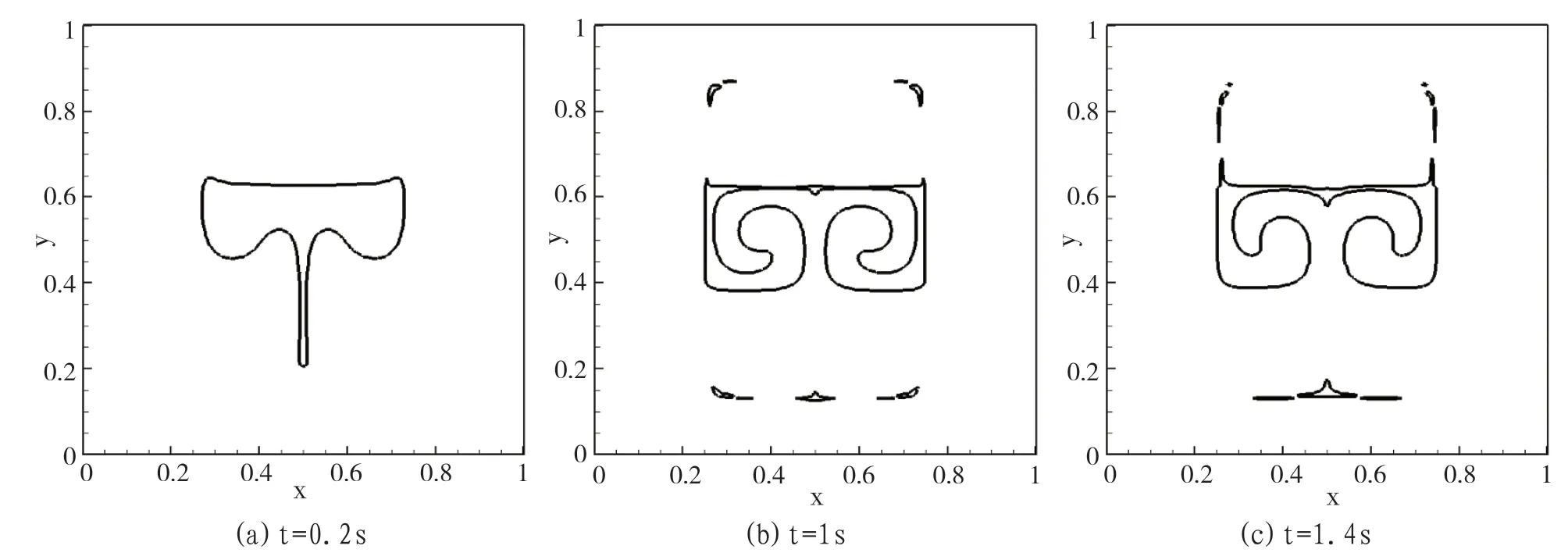
图2 多涡剪切流场的模拟结果(T=2s)

4 结论

数值结果表明：CVOFLS 方法对多涡剪切流场的数值模拟效果良好，其数值结果验证了CVOFLS 方法的准确性，同时表明该方法在数值界面模拟方面，具有更高的计算效率以及更好的界面模拟精度。