一种快速的软件频率计算方法

李肖博，姚 浩，于 杨，习 伟，蔡田田

一种快速的软件频率计算方法

李肖博，姚 浩，于 杨，习 伟，蔡田田

(南方电网数字电网研究院有限公司，广东 广州 510640)

频率测量是电力系统测控装置和保护装置的基本功能。频率测量的快速性和准确性将深度影响电力系统测控和保护装置的性能，从而影响到电力系统的稳定性。为提高频率测量的快速性，提出了一种全新的频率测量算法。该算法可以在5/4周波内测量出被测对象的频率，具有极强的实时性。首先对计算傅里叶级数实部的核函数进行移相。然后分别采用移相前后的核函数对原始信号进行傅里叶变换，求取实部信号。接着利用两个实部信号过零点的时间差计算出信号频率。最后使用Matlab仿真和保护装置实测对该算法进行了验证。验证结果显示：所提测频算法对频率的测量满足精度要求；相对于现有算法，对渐变频率的跟踪速度有较大的提高。

频率测量；傅里叶级数；核函数；移相；Matlab

0 引言

频率测量是电力系统的一个重要基础功能，频率测量的准确性对电力系统有非常重要的作用。电网中只要需要控制的部分大多需要用到频率测量，例如水轮机等发电系统控制[1-2]、电网调频[3-4]、新能源应用和微电网调度[5-7]、负荷特性判断等[8-9]。在相量计算领域，频率测量的快速性和准确性对数字电能计算算法[10]、交流信号有效值计算精度[11]、谐波分析算法的精度[12]、模拟量有效值计算[13]、谐波相量测量算法[14]，同步相量修正[15]和模拟量基波幅值计算[16]等相量计算有非常大的影响。

基于不同的原理，已有相当多的频率测量方法。文献[17]通过调整采样间隔来进行频率跟踪，方法简单易用，但是采样间隔的调整精度本身依赖频率的测量精度。文献[18]通过设置一个自适应陷波器来更精确地测量频率，但是方法相对比较复杂。文献[19]通过曲线拟合结合泰勒级数展开的方法来测量频率；文献[20]通过3个连续模拟量的采样点来测量频率。文献[19]和文献[20]的测频速度都比较快，但是频率测量误差较大。文献[21]通过设计数字滤波器来滤除测频信号中的谐波分量，该频率测量算法对含有谐波的信号也具有有效性。

众所周知，周期信号的最小正周期的倒数为其频率。对于没有任何噪声的正弦信号，其相邻的同方向变化的两个过零点之间的时间差即为这个正弦信号的正周期，这个正周期的倒数即为正弦信号的频率。这种通过检测同方向变化的两个过零点来测量频率的方法概念清楚，方法简单，但是容易受到噪声的影响。

电力系统中大部分交流量的主要成分一般为正弦信号。但是这些正弦信号基本都含有噪声。其中一种噪声是由频率偏移造成的。文献[17]提出了一种频率跟踪方法，通过调整采样间隔的方法来减少频率偏移时的频率测量误差，方法简单但仅适用于频率偏移额定频率不多的情况。文献[20]提出了一种通过3个连续采样点来快速计算频率的方法，该方法简单，容易实现，对于任何频率的信号都能够准确测量，频率偏移额定频率较多的场合也能够应用，但是未能解决噪声的影响。

在电力系统中，另外一种典型的噪声为谐波和直流分量。对于噪声主要为谐波和直流分量的信号，傅里叶级数是去除噪声最有效的方法。文献[22]经过理论推导得出傅里叶级数得到的基波实部和虚部两个信号的频率与原信号的频率一致。通过测量基波实部或者虚部的相邻同方向变化的两个过零点之间的时间差来测量正周期，继而对正周期求倒数来计算频率。该方法能够消除谐波和直流分量的影响，但是测频的时间窗为2个周波，测频速度较慢。文献[23]对实部信号和虚部信号相乘，并采用相邻过零点的方法测频，测频的时间窗缩小到1+1/4个周波，但是在有些实时性要求较高的场合，速度仍然较慢。

1 傅里叶级数基波实虚部的特征

1.1 实虚部频率等于原信号频率

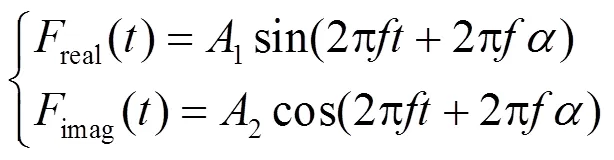
1.2 实虚部过零点相差1/4周期

正弦信号相邻同方向过零点之间的时间差为一个周波，而相邻过零点之间的时间差为半个周波，以相邻过零点之间的时间差来计算频率，可以节省半个周波的时间。

傅里叶级数基波实部是一个正弦信号，虚部是一个余弦信号，这两个信号之间的相位相差1/4周期。文献[23]把傅里叶级数基波实部和虚部相乘，得到一个相邻过零点之间时间差为原信号1/4周期的信号，利用相乘后的信号相邻过零点测频，测频的时间窗缩小到1+1/4个周波。

2 新型频率测量算法原理

2.1 算法原理

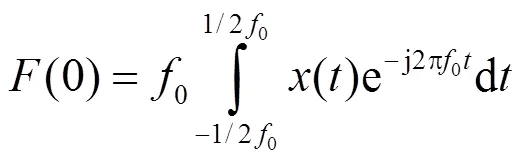
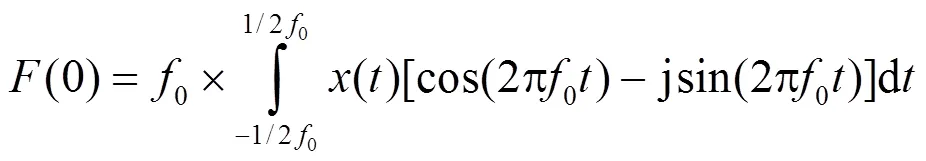
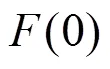
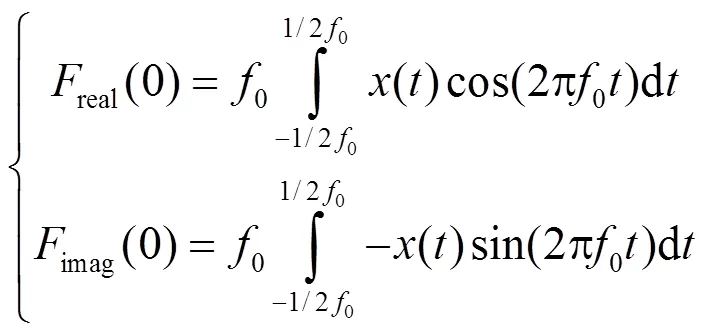
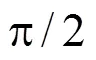
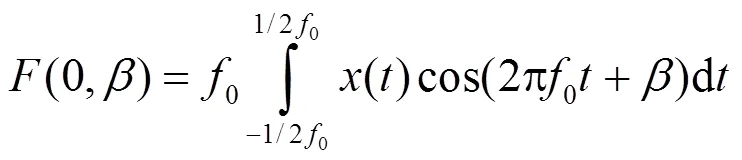
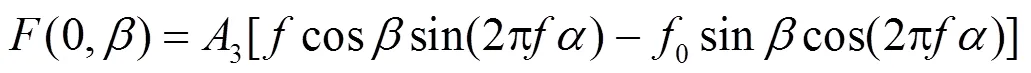
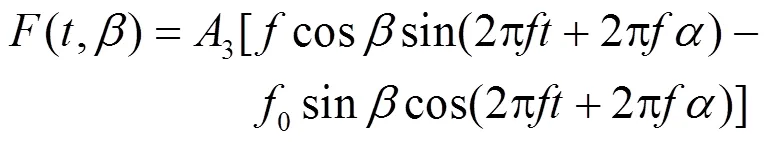
令：

则：

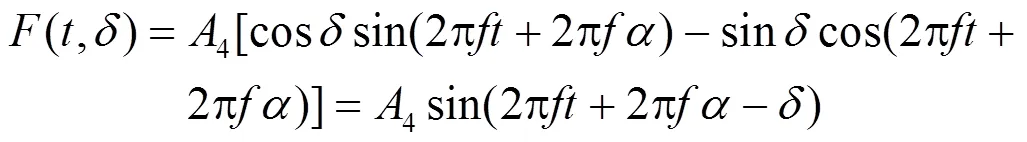
由式(9)可以得到

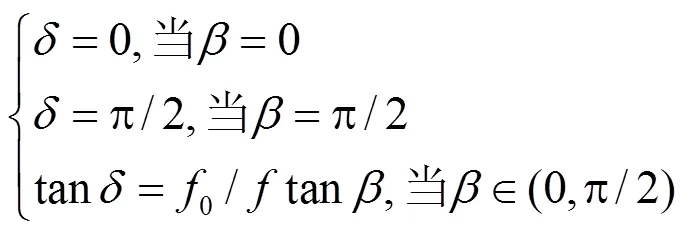
2.2 算法实现

依据2.1节的分析结果，可以采用如下方法来测频，提高测频的速度。

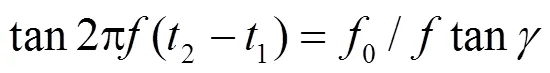
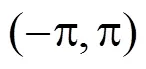
Matlab仿真和装置采用离散方法测量出来的频率乘以对应的修正系数得出实际的频率。

在保护测控装置中，可以把计算出来的修正系数作为一个表格存储起来，实际测频时，可以通过查表的方式查询修正系数。对于存储空间比较紧张的场合，可以事先采用拟合的方式得出图1所示曲线的函数表达式，实际测频时，根据频率计算修正系数。

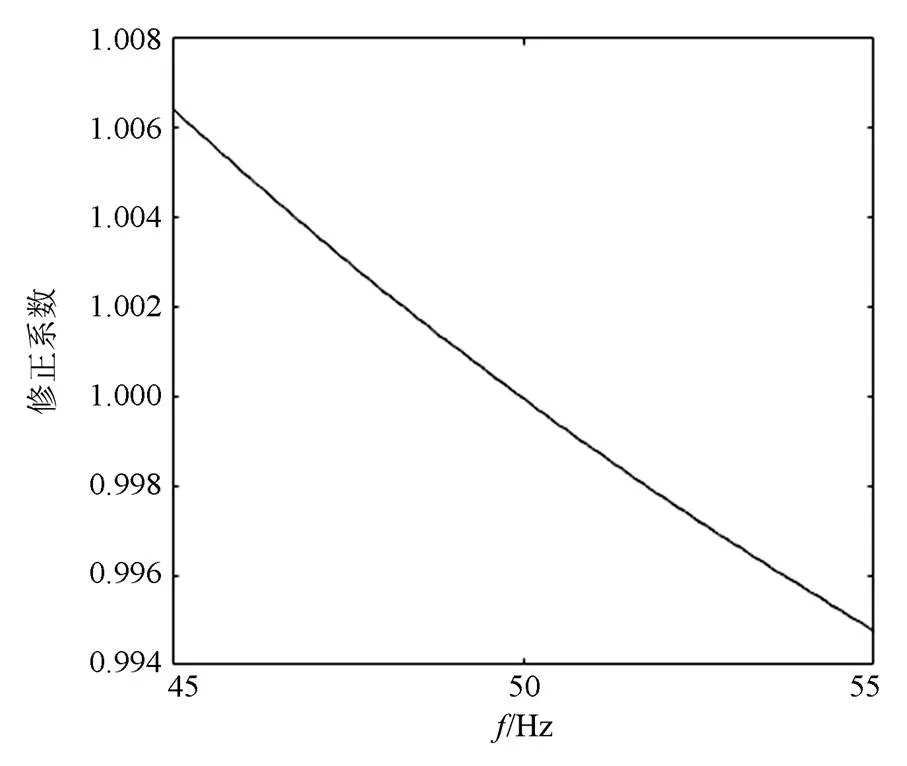
图1 修正系数与频率的关系

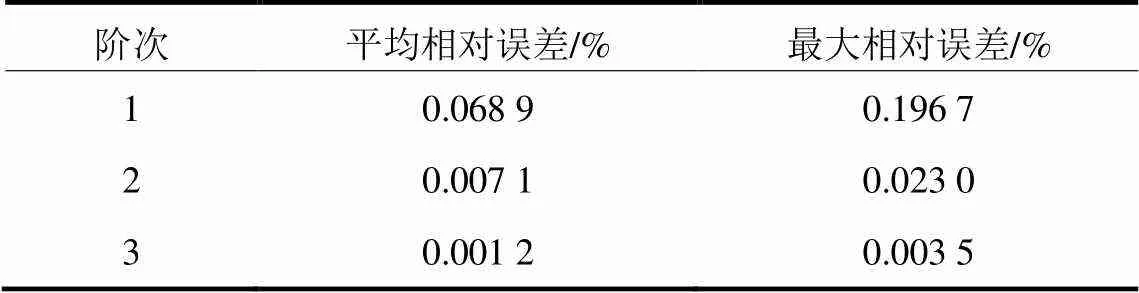
表1 多项式拟合误差分析

从表1可以看出，多项式阶数为1，即线性拟合时，修正系数的最大误差接近0.2%，当频率为50 Hz时，其带来的误差为0.1 Hz，不能满足频率测量精度的要求。随着多项式阶次的提高，修正系数的拟合误差快速降低，当多项式阶次为3时，修正系数的最大误差为0.003 5%，当频率为50 Hz时，其带来的误差为0.001 8 Hz，基本不会影响频率的测量精度。

3 仿真分析

3.1 单一频率仿真

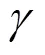
在图2中所示的200 ms区间内，各个频率的平均绝对误差和最大绝对误差如表2所示。

从图2可以看出，在200 ms区间内，频率仿真曲线的误差均没有超过0.02 Hz。从表2可以看出，实测频率的最大绝对误差仅为0.018 1 Hz。频率测量精度较高。

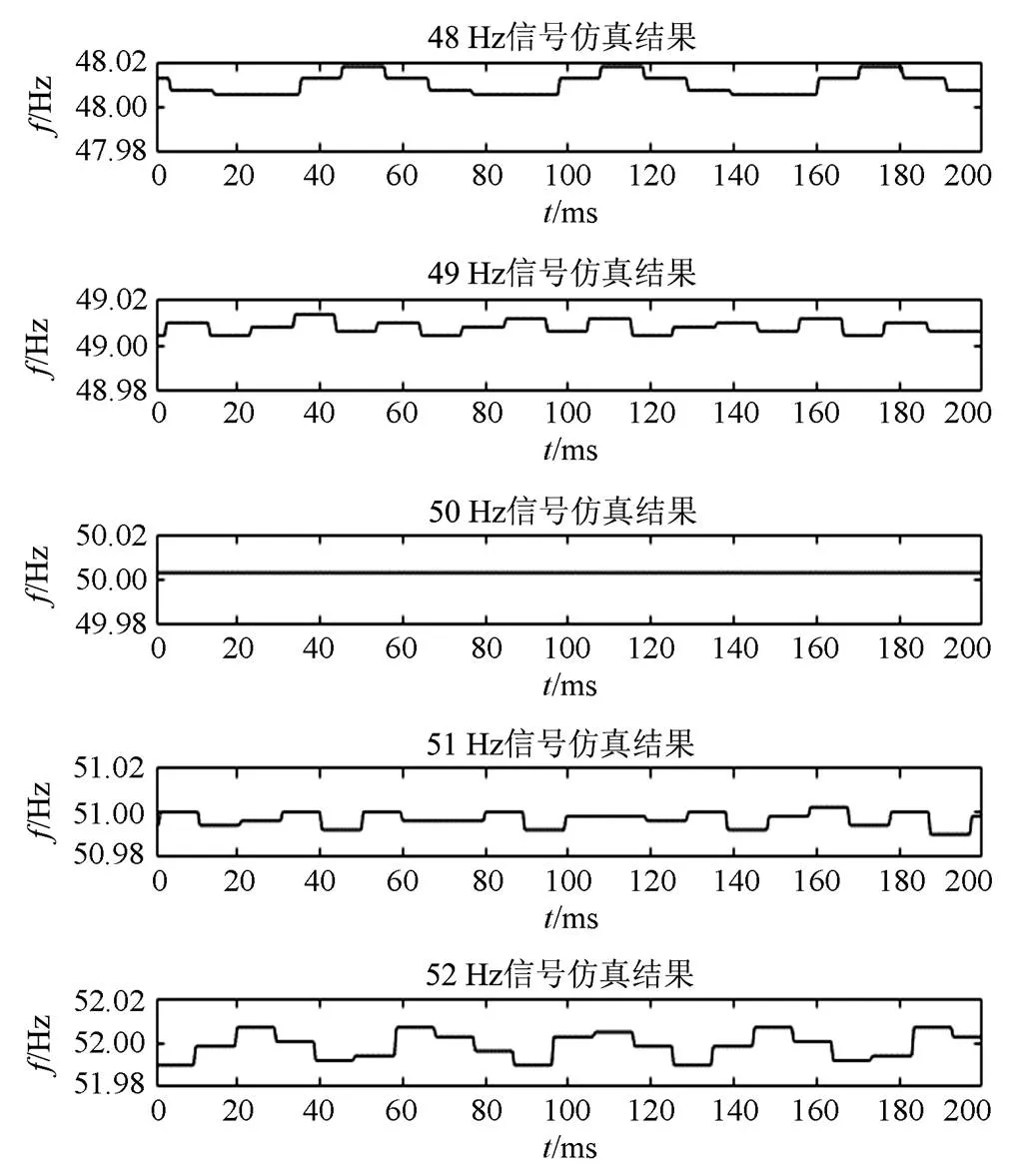
图2 各种频率的仿真结果

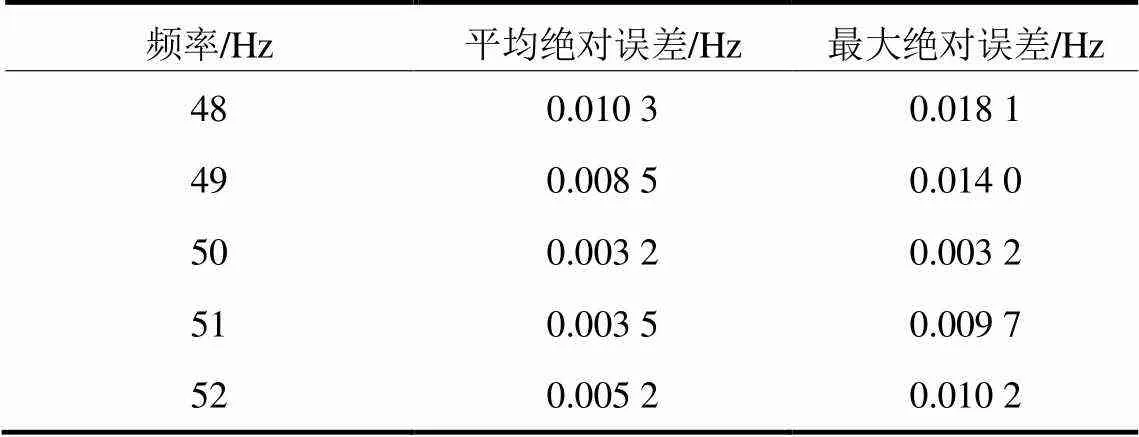
表2 各种频率的仿真误差分析

3.2 渐变频率仿真

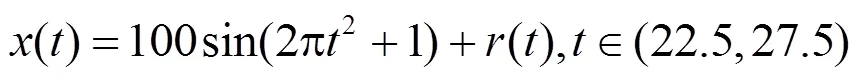
图3中：两个小图中的实线为理论计算的频率曲线；虚线为采用文献[23]中的测频算法计算的频率曲线；点画线为采用本文测频算法计算的频率曲线。上半部分图形为45～55 Hz整个频率范围的仿真结果图；下半部分图形为局部放大的仿真结果图。

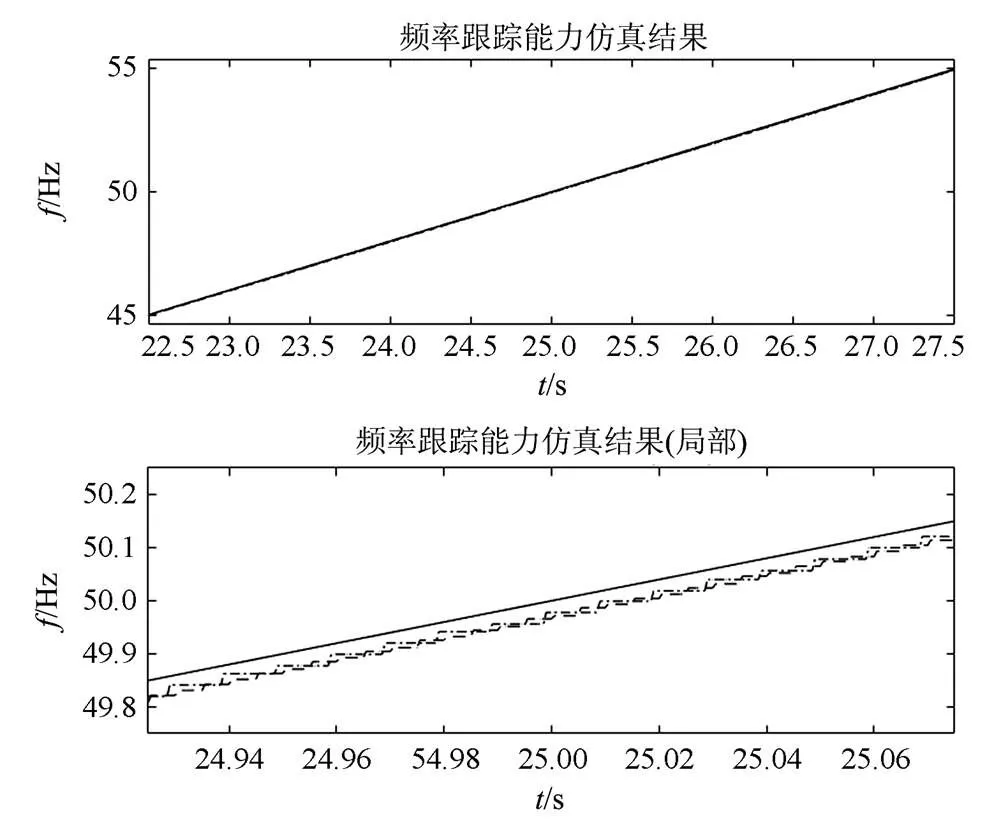
图3 渐变频率的仿真结果

从图3中可以看出，相对于虚线，点画线更加接近实线，验证了本文测频算法对渐变频率具有更快的跟踪速度。

在45～55 Hz整个范围内，文献[23]和本文测频算法的平均绝对误差如表3所示。

表3 渐变频率的跟踪误差

从表3中可以看出，本文算法的跟踪误差比文献[23]的跟踪误差小0.0322-0.0277=0.0045 Hz。本文算法对频率的跟踪速度更快，相应的跟踪精度更高。

4 保护测控装置实际分析

在保护测控装置中用本文的算法进行频率测量，保护测控装置采用TI公司的OMAPL138作为CPU，使用16位的ADC芯片对输入模拟量以每秒2 000点的固定采样率进行采样。

装置在初始化程序中对系统频率、采样率和核函数移相角等进行初始化，初始化程序的流程图如图4所示。

装置采用电压通道来进行测频，输入装置的电压有效值为50 V，频率为48～52 Hz范围内的不同频率。装置实测时的接线图如图6所示。

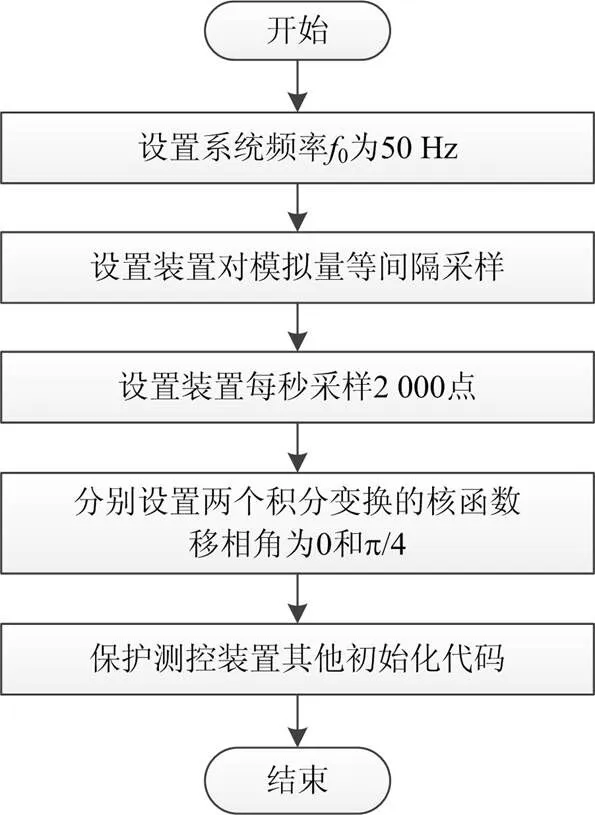
图4 初始化程序流程图

图5 中断程序流程图

图6 装置实测的接线图

图6中，继电保护试验仪AB端输出的电压接到保护测控装置用于测频的电压通道的外部端子C和D上。改变继电保护试验仪输出电压的频率，验证装置对频率测量的准确性。装置对输入模拟量实测的频率如图7所示。

图7 各种频率的装置实测结果

在图7所示的200 ms区间内，各个频率的平均绝对误差和最大绝对误差如表4所示。

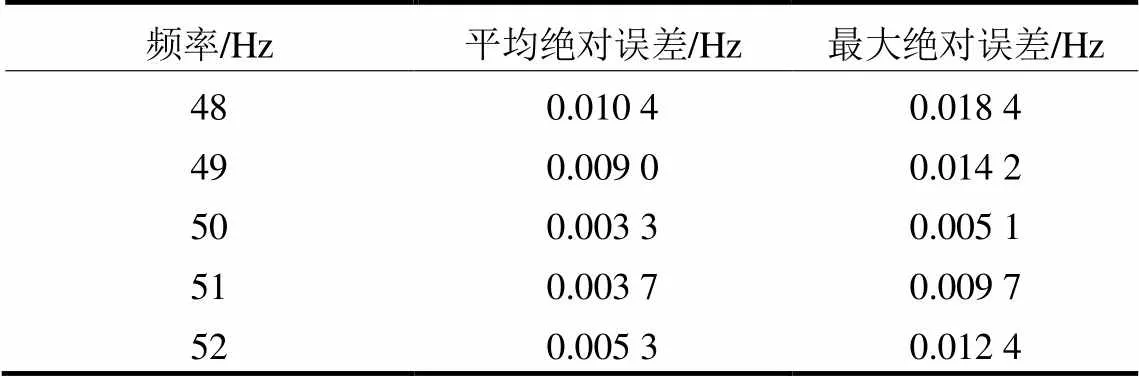
表4 不同频率的装置实测误差分析

对比表4和表2可以看出，装置实测结果的平均绝对误差和最大绝对误差相对于Matlab仿真都有所增大，这是因为Matlab仿真时输入的是一个完美的信号，而装置实测时，输入的信号或多或少存在一定的噪声。

虽然装置实测的误差比仿真有所增大，但是从图7可以看出，在200 ms区间内，频率仿真曲线的误差也均没有超过0.02 Hz。从表4可以看出，实测频率的最大绝对误差仅为0.018 4 Hz。频率测量精度比较高，能够满足保护测控装置的精度要求。

5 结论

本文提出了一种新的测频方法，通过采用两个经过不同移相核函数的傅里叶变换后的曲线来进行测频，可以在小于1+ 1/4周波的时间内测量出信号的频率。相对于现有的基于过零点的系列测频算法，测频速度大幅提高。经过Matlab仿真和保护测控装置实际测试，结果表明测频的精度满足现场的需求。由于测频速度的提高，本方案对渐变频率的跟踪速度相对于现有算法有较大的提高。

应用于保护测控装置时，本文提出的算法未考虑保护测控装置可以根据频率调整采样周期，即频率跟踪能力。后续可以研究考虑频率跟踪之后，本文提出的算法在保护测控装置中的性能。

[1] 丁理杰, 刘姗梅, 史华勃. 水电高占比电网中水轮机模型对频率振荡特性影响及其适应性分析[J]. 电力系统保护与控制, 2021, 49(12): 174-180.

DING Lijie, LIU Shanmei, SHI Huabo. Influence of a turbine model on frequency oscillation characteristics and its adaptability in a high hydro-ratio power grid[J]. Power System Protection and Control, 2021, 49(12): 174-180.

[2] 海世芳, 孙士云, 范小红, 等. 计及频率特性的感应电动机参数变化对负荷特性的影响[J]. 电力系统保护与控制, 2019, 47(8): 17-25.

HAI Shifang, SUN Shiyun, FAN Xiaohong, et al. Influence of induction motor parameter change considering frequency characteristics on load characteristics[J]. Power System Protection and Control, 2019, 47(8): 17-25.

[3] WANG Cuihong, ZHAO Yafei, CHEN Yangquan. The controllability, observability, and stability analysis of a class of composite systems with fractional degree generalized frequency variables[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(3): 859-864.

[4] 李咸善, 董鑫, 程杉, 等. 微电网群频率调整的分层协调控制策略[J]. 电力系统保护与控制, 2020, 48(21): 1-14.

LI Xianshan, DONG Xin, CHENG Shan, et al. Hierarchical coordinated control strategy for frequency adjustment of microgrid groups[J]. Power System Protection and Control, 2020, 48(21): 1-14.

[5] PADHY S, PANDA S. Application of a simplified Grey Wolf optimization technique for adaptive fuzzy PID controller design for frequency regulation of a distributed power generation system[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 21-36.

[6] 郄朝辉, 黄慧, 李威, 等. 周期通信对储能系统参与电网调频的影响分析[J]. 电力系统保护与控制, 2020, 48(1): 41-47.

QIE Zhaohui, HUANG Hui, LI Wei, et al. Analysis of the influence of periodic communication on the participation of energy storage system in power grid frequency modulation[J]. Power System Protection and Control, 2020, 48(1): 41-47.

[7] 张刘杰, 肖仕武, 黄松柏. 基于灵敏度的孤网动态频率偏移峰值分析和调速系统参数优化[J]. 电力系统保护与控制, 2020, 48(2): 137-143.

ZHANG Liujie, XIAO Shiwu, HUANG Songbai. Dynamic frequency offset peak analysis and speed control system parameter optimization of isolated networks based on sensitivity[J]. Power System Protection and Control, 2020, 48(2): 137-143.

[8] AZARBAHRAM A, AMINI A, SOJOODI M. Resilient fixed-order distributed dynamic output feedback load frequency control design for interconnected multi-area power systems[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(5): 1139-1151.

[9] ZHANG Yi, LIU Xiangjie, QU Bin. Distributed model predictive load frequency control of multi-area power system with DFIGs[J]. IEEE/CAA Journal of Automatica Sinica, 2017, 4(1): 125-135.

[10] 张秋雁, 魏伟, 李红斌. 基于Lagrange插值频率估计的数字电能计量算法[J]. 电测与仪表, 2017, 54(5): 80-84.

ZHANG Qiuyan, WEI Wei, LI Hongbin. Digital power metering algorithm based on Lagrange interpolation frequency estimation[J]. Electrical Measurement & Instrumentation, 2017, 54(5): 80-84.

[11] 孙俊香. 提高交流信号真有效值测量精度的改进方法[J]. 电测与仪表, 2011, 48(11): 20-23.

SUN Junxiang. The method to improve the accuracy of true effective value in ac-sampling measurement[J]. Electrical Measurement & Instrumentation, 2011, 48(11): 20-23.

[12] 王纲, 李剑飞, 陈隆道, 等. 一种基于频率补偿的改进插值谐波分析算法[J]. 电力系统保护与控制, 2018, 46(24): 1-7.

WANG Gang, LI Jianfei, CHEN Longdao, et al. An improved interpolation harmonic analysis algorithm based on frequency compensation[J]. Power System Protection and Control, 2018, 46(24): 1-7.

[13] 付振虎, 赵鑫. 一种频率偏移时求取有效值的方法[J]. 山东理工大学学报(自然科学版), 2012, 26(2): 91-94.

FU Zhenhu, ZHAO Xin. A method for valid value measurement with frequency deviation[J]. Journal of Shandong University of Technology (Natural Science Edition), 2012, 26(2): 91-94.

[14] 陈克绪, 陈垒, 胡涛, 等. 计及较大频率偏移的谐波相量测量算法[J]. 电测与仪表, 2020, 57(24): 22-28.

CHEN Kexu, CHEN Lei, HU Tao, et al. Harmonic phasor estimation algorithm considering large frequency deviations[J]. Electrical Measurement & Instrumentation, 2020, 57(24): 22-28.

[15] 李梅, 丁涛, 顾伟, 等. 频率偏移情况下的同步相量修正[J]. 东南大学学报(自然科学版), 2011, 41(4): 744-749.

LI Mei, DING Tao, GU Wei, et al. Synchronous phasor correction under frequency offset[J]. Journal of Southeast University (Natural Science Edition), 2011, 41(4): 744-749.

[16] 郑作伟, 江卫良, 郝后堂, 等. 频率偏移时基波幅值计算误差对保护的影响及其改进算法[J]. 电力科学与工程, 2016, 32(3): 17-21.

ZHENG Zuowei, JIANG Weiliang, HAO Houtang, et al. Effects of the fundamental amplitude’s calculational errors when frequency offset on protections and its improved algorithm[J]. Electric Power Science and Engineering, 2016, 32(3): 17-21.

[17] 曾院辉, 李延新. 一种软件频率的跟踪方法[J]. 电力系统自动化, 2005, 29(21): 92-94.

ZENG Yuanhui, LI Yanxin. Method of soft frequency tracking[J]. Automation of Electric Power Systems, 2005, 29(21): 92-94.

[18] 王雅丽, 虞莉娟, 张华军, 等. 基于自适应陷波器的电网频率估计方法[J]. 电测与仪表, 2018, 55(24): 121-127.

WANG Yali, YU Lijuan, ZHANG Huajun, et al. Frequency estimation method for power grid based on adaptive notch filter[J]. Electrical Measurement & Instrumentation, 2018, 55(24): 121-127.

[19] 王东, 毕潇映. 一种电力系统频率的实时估算方法[J]. 继电器, 2004, 32(18): 17-19.

WANG Dong, BI Xiaoying. A new method of real-time estimation for power system frequency[J]. Relay, 2004, 32(18): 17-19.

[20] 张英, 牟龙华. 电力系统频率测量及跟踪[J]. 电力系统及其自动化学报, 2003, 15(3): 35-36.

ZHANG Ying, MU Longhua. Frequency measuring and tracking of power systems[J]. Proceedings of the CSU-EPSA, 2003, 15(3): 35-36.

[21] 郭彦东, 张占江. 一种新的电力系统频率实时测量方法[J]. 自动化技术与应用, 2006, 25(12): 62-64.

GUO Yandong, ZHANG Zhanjiang. Real-time measurement of the power system frequency[J]. Techniques of Automation and Applications, 2006, 25(12): 62-64.

[22] 方存洋, 陈玉兰, 潘汉广. 一种实用的软件测频算法[J]. 电力自动化设备, 2007, 27(12): 36-39.

FANG Cunyang, CHEN Yulan, PAN Hanguang. Power frequency measurement algorithm[J]. Electric Power Automation Equipment, 2007, 27(12): 36-39.

[23] 郑作伟, 江卫良, 郝后堂, 等. 一种快速软件频率跟踪法[J]. 广东电力, 2012, 25(7): 75-77.

ZHENG Zuowei, JIANG Weiliang, HAO Houtang, et al. A fast software frequency tracking method[J]. Guangdong Electric Power, 2012, 25(7): 75-77.

A fast software frequency calculation method

LI Xiaobo, YAO Hao, YU Yang, XI Wei, CAI Tiantian

(China Southern Power Grid Digital Grid Research Institute Co., Ltd., Guangzhou 510640, China)

Frequency measurement is the basic function of power system measurement and of a control device and protection device. The rapidity and accuracy of frequency measurement will seriously affect the performance of power system measurement and the protection device, thus affecting the stability of the power system. In order to improve the rapidity of frequency measurement, a new frequency measurement algorithm is proposed. The algorithm can measure the frequency of the measured object in 5/4 cycle, and has strong real-time performance. First, the kernel function for calculating the real part of a Fourier series is phase shifted. Then the kernel function before and after phase shift is used to Fourier transform the original signal to obtain the real part of the signal. After that, the signal frequency is calculated by using the time difference between the zero crossing of two real part signals. Finally, the algorithm is verified by Matlab simulation and actual measurement of a protection device. The tests show that the proposed algorithm meets the accuracy requirements; the tracking speed of gradually changed frequency is greatly improved compared to that of existing algorithms.

frequency measurement; Fourier series; kernel function; phase shift; Matlab

10.19783/j.cnki.pspc.210477

中国南方电网有限公司科技项目资助(ZBKJXM 20180500)；国家重点研发计划资助(2017YFB0904900, 2018YFB0904902)

This work is supported by the Science and Technology Project of China Southern Power Grid Co., Ltd. (No. ZBKJXM20180500).

2021-04-23；

2021-08-13

李肖博(1980—)，男，工学硕士，高级工程师，主要研究方向为电力系统继电保护。E-mail: lixb1@csg.cn

(编辑 魏小丽)