基于VSG控制的微网逆变器工频振荡现象研究

马 也，史丽萍，李 衡，李 昊，孙裔峰，缪荣新

基于VSG控制的微网逆变器工频振荡现象研究

马 也，史丽萍，李 衡，李 昊，孙裔峰，缪荣新

(中国矿业大学电气与动力工程学院，江苏 徐州 221008)

分布式电源多采用电力电子变流器作为接口与电网进行能量交互，虚拟同步发电机控制技术因模拟传统同步机内外部性能优良的特点成为目前研究的热点。但电力电子装置因其动作快速性容易激发线路电感，其电流的瞬态过程会对系统产生不利影响。考虑线路电感的瞬变过程，建立系统输出功率的动态小信号模型，分析产生振荡的原因与系统输出阻抗有关。采用一种新型阻尼控制策略，在电压外环引入虚拟复阻抗，可以重塑系统阻抗特性，达到抑制功率振荡的目的。通过仿真与实验，验证了VSG中的工频振荡现象以及所提控制策略的有效性。

虚拟同步发电机；动态小信号模型；工频振荡；虚拟复阻抗

0 引言

能源匮乏与环境恶化的双重压力迫使人类寻找可替代的能源。随着人类对光伏、风电利用技术的不断突破，各种新能源发电得到蓬勃发展[1-2]。为了应对大规模分布式电源并网对系统稳定性的不利影响，采用微电网形式接纳分布式电源逐渐成为电力系统的另一种工作模式[3-7]。与传统依靠同步发电机发电模式不同，分布式能源发电大多采用电力电子装置与大电网相连接。然而，电力电子设备作为电网接口不同于传统同步机，几乎不具备转动惯量与阻尼特性。虚拟同步发电机(Virtual Synchronous Generator, VSG)由此提出，并成为研究热点[8-12]。

虚拟同步发电机控制技术通过在功率环引入有功与无功下垂特性，并将同步发电机的电磁方程引入到控制环路中，不仅可以参与电网的调频调压，还增强了系统的惯性与阻尼[13-17]。但是电力电子器件的快速反应能力不可消除，可能会给系统带来稳定性问题，比如激发线路电感，使电流、功率等参量产生剧烈波动[18-19]。文献[20-23]重点关注了风力发电系统的次同步振荡问题，主要源于机组与换流器之间的相互作用对系统阻抗产生影响，导致系统阻抗呈现主感性。文献[24]论证了光伏系统可能与感性电网发生次同步频率的电气谐振，指出电流功率中可能在工频附近存在谐波分量的问题，改变内环控制参数可在一定程度上阻尼谐振现象。文献[25]针对高频谐振进行研究，设计一种修改内环控制算法，将逆变器等效输出阻抗修正呈正阻性以抑制高频谐振。文献[26]分析了并网逆变器的谐波谐振特性，提出有源阻尼控制策略，重塑系统阻抗以抑制高频谐振。但是对于系统输出的功率振荡未做详细阐述。文献[27-29]指出同步角频率谐振的问题，通过建立VSG功率环的小信号模型分析了振荡产生机理，而在抑制策略上没有给出理论分析。

文章在上述文献研究的基础上，对同步频率振荡现象进行理论层面详细分析，建立了考虑电感磁链瞬态过程的功率环小信号模型，推导出有功功率与阻抗角、无功功率与电压的小扰动下的精确关系，得到了功率发生工频振荡的原因在于微电网系统输出阻抗中电阻过小，使得功率环开环传递函数的极点在工频处靠近平面的虚轴引发输出功率发生振荡。因此，提出一种新型阻尼控制策略，通过在电压电流双环控制里引入虚拟复阻抗，重塑系统输出阻抗为阻性，实现对工频振荡的抑制。通过仿真与实验，结果证明了所提控制策略的有效性。

1 VSG工频振荡原因分析

典型虚拟同步发电机控制的并网逆变器控制框图如图1所示。VSG本体主要包含有功控制环与无功控制环，通过这两个环节的构造，可以模拟传统同步发电机调压调频的功能。再通过对VSG控制输出的两个参量进行双闭环控制，便可以生成开关管的驱动电压信号。

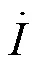
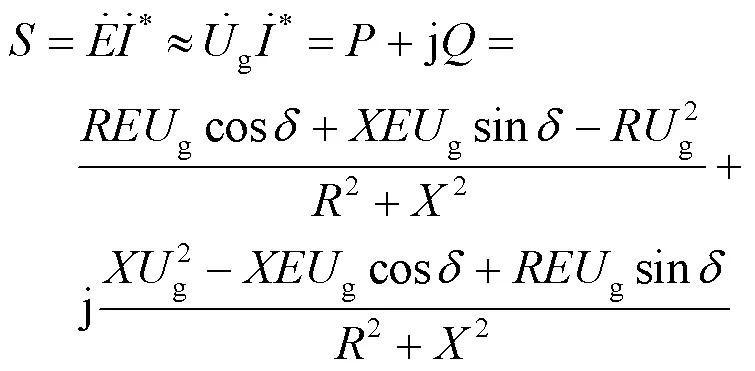
不考虑线路电阻时式(1)化简为

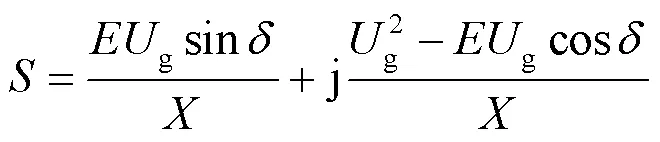
在电力系统潮流分析中，有功-阻抗角，无功-电压是两组非常重要的关系，考虑到传统同步发电机有较大的转动惯量和阻尼系数，所以对于传统的电力系统，工程上常采用准静态分析法，其表现形式为有功功率对阻抗角、无功功率对逆变输出电压采用求偏微分方程的方式，可以得到式(3)。

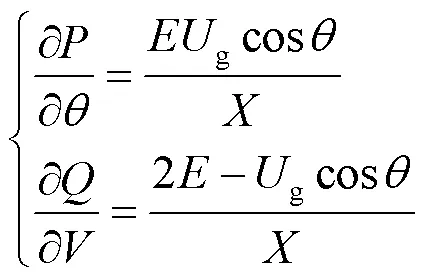
但准静态分析法的弊端在于考虑系统的各部分均处于稳定状态或者相对缓慢的动态过程，不考虑电感、电容等无源元件的电磁瞬变。但是对于大多数的微电网系统，大都采用电力电子器件实现对电网的接入，对于电力电子器件来说，电磁瞬变将对系统产生极大的干扰，所以要给出更严格的数学推导，以表征电压与电流的微小扰动对整个系统输出的影响，文章借助于小信号模型分析。

有功功率与无功功率影响因素不同，所以要对这两者分别进行研究。有功功率可以表示为

写成分量形式为

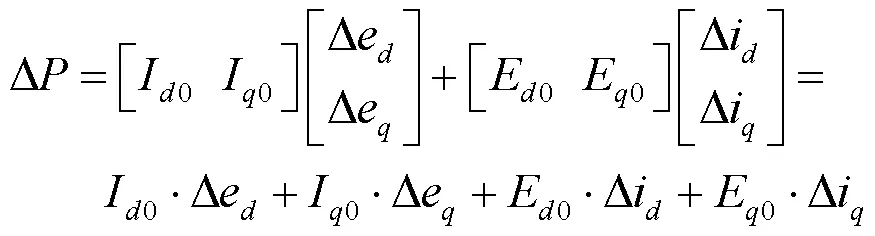
由基尔霍夫电压定律以及空间向量理论，求取式(5)中8个分量推导出精确的动态功角关系式：

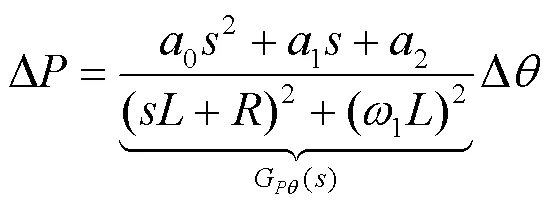
同理，无功功率关于电压的传递函数与有功功功率关于阻抗角的传递函数推导过程类似，给出表达式(7)。

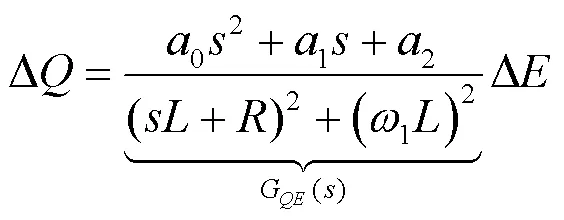
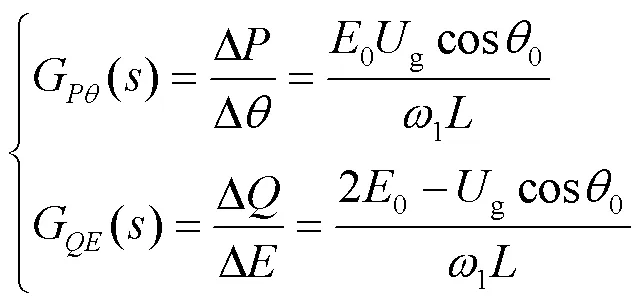
式(8)恰好符合传统同步发电机准静态分析的关系式(3)，验证了所推导精确模型具有一般性。式(6)与式(7)给出了全频域功率的表达式，通过观察两式可以发现一个共同点：即全频域的有功-阻抗角与无功-逆变输出电压的关系式含有相同的共轭极点：

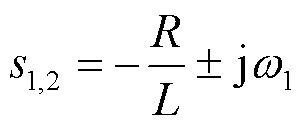
在中高压微网系统，电阻通常较小。当这两个极点要靠近虚轴时，由自动控制理论可知，将在同步角频率1处产生谐振现象。通过对有功功率与无功功率精确计算式的推导可知，有功与无功响应都将在同步角频率处发生振荡[19]。

2 工频振荡特性分析

2.1 有功环特性分析

对VSG有功环做小信号模型分析，可以得到图2所示的控制框图。

图2 VSG有功环小信号模型控制框图

图2中，为转动惯量，为阻尼系数，G()是功角传递函数，是有功环的重要环节。根据图2，推导出有功功率开环传递函数为

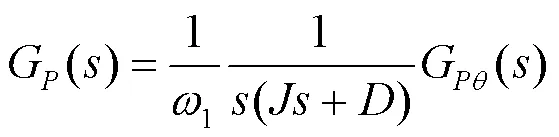
图3 GP(s)的伯德图

Fig. 3 Bode diagram of GP(s)

由图4可以看出，在1 s时刻阻抗角发生了5º的跳变，而对应的有功功率会产生逐渐衰减的振荡，通过观察1.5～1.6 s的波形，可以发现其振荡的频率是50 Hz，充分验证了在VSG控制的微网逆变器系统中存在着功率工频振荡现象。

2.2 无功环特性分析

同有功环分析一样，首先建立无功电压环的小信号模型控制框图如图5所示。

图4 GPθ(s)的阶跃响应

图5VSG无功环小信号模型控制框图

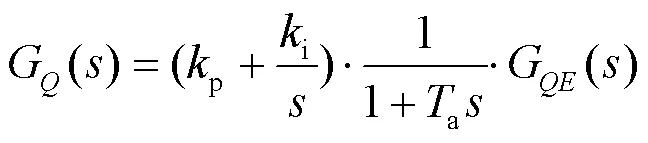
绘制无功控制环的开环传递函数伯德图，如图6所示。

图6 GQ(s)的伯德图

Fig. 6 Bode diagram of GQ(s)

通过图6可以发现，同步发电机系统无功控制环的开环传递函数的相角裕度与幅值裕度均大于零而且两者均变化平缓，说明其具有相当大的稳定性和系统抗扰动能力；而对于VSG控制下的逆变系统而言，尽管其相角裕度与幅值裕度也大于零，但是不可忽视谐振峰的影响，其后果必然导致在时域阶跃响应下系统的超调将远超出稳态值。

对动态小信号模型下的传递函数G()进行时域阶跃响应分析，如图7所示。给定输入在1 s时刻产生0.2 V的阶跃变化，可以看到输出∆发生了振荡现象，且振荡的频率依然为50 Hz。所以，VSG输出的无功功率易发生工频振荡。

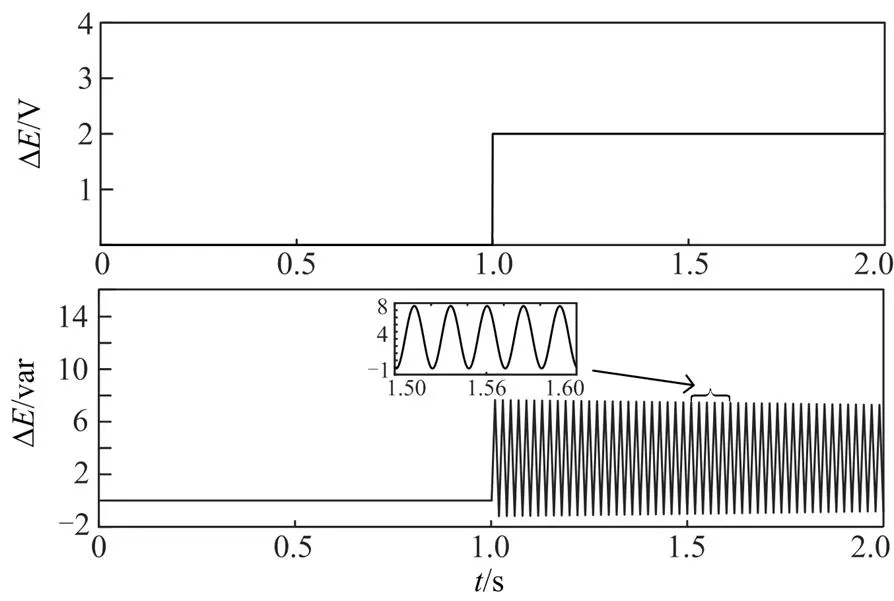
图7 GQE(s)的阶跃响应

3 工频振荡的抑制策略研究

对于中高压微电网系统，VSG输出阻抗呈现出电感性，而整个VSG系统的阻抗从理论上为VSG输出阻抗与传输线路阻抗之和，如果保证这个和值不再呈现出明显的感抗时，也就可以抑制功率工频振荡的发生。

通过对谐振产生的理论分析可知，造成谐振现象的主要原因在于线路电阻过小，导致有功环与无功环的开环传递函数的极点靠近虚轴，尽管极点的实部小于0，系统最终趋于稳定状态，但是需考虑谐振处的幅值影响，易在工频处引发功率振荡。已提出的虚拟复阻抗技术成为解决问题的方法。引入虚拟阻抗后，VSG电路模型如图8所示。

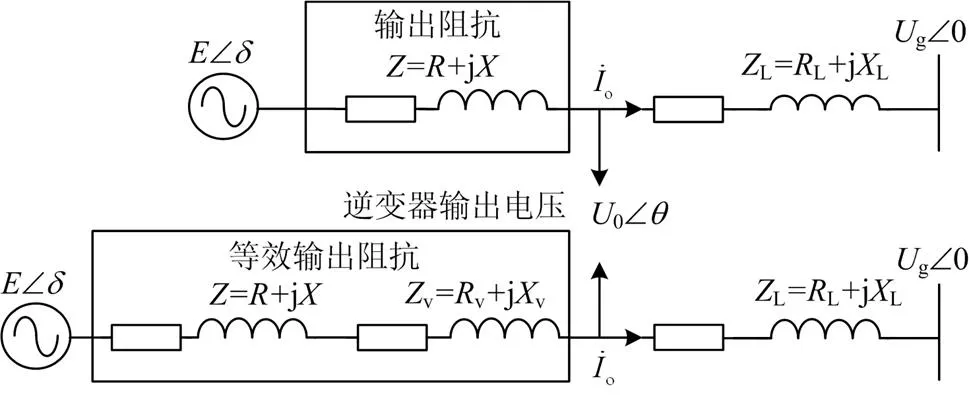
图8 引入虚拟阻抗前后VSG电路模型

引入虚拟阻抗后系统等效输出阻抗可以表示为

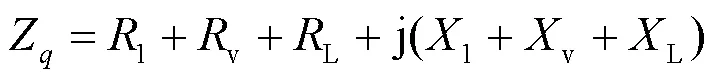
通过以上分析，在电压与电流的控制环引入复阻抗，重塑系统的输出阻抗，可以实现目标极点远离虚轴，落在平面的左半边。基于虚拟复阻抗的电压控制策略，设计方案为：VSG功频调节器与励磁调节器输出计算合成参考电压ref()，在电压外环引入虚拟复阻抗v对参考电压进行跟踪控制，具体控制结构如图9所示。

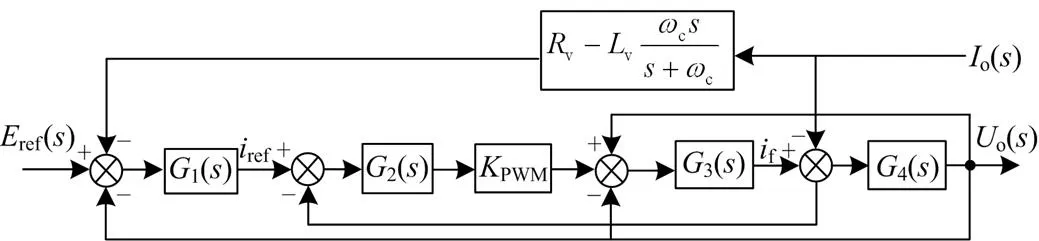
图9 引入虚拟复阻抗的双环控制框图

由图9可以得到VSG双环控制传递函数为

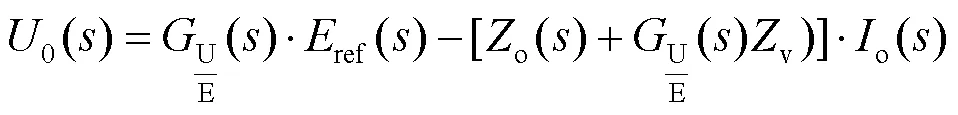
其中：

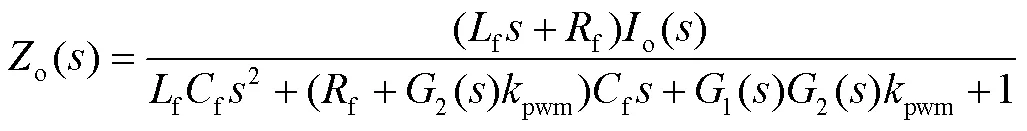
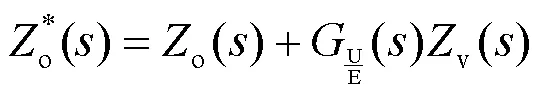
给定具体的仿真参数，保持虚拟电感V=1 mH，绘制出引入虚拟阻抗后的控制系统传递函数的伯德图如图10所示。

图10 虚拟电阻改变时系统输出阻抗伯德图

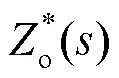
考虑裕度问题，v取值不宜过小，但是虚拟电阻v的上限有相关要求。文献[30]指出较大的输出阻抗会引起实际的VSG输出电压相比于参考电压产生较大压差，而且在多机并联系统，过大的输出阻抗对于均流效果也会产生负面影响。故本文综合考虑裕度与误差问题，选取虚拟电阻v的值为1 Ω。虚拟电感构成的环节包含了低通滤波环节，对于滤除电流因微分产生的高频噪声有很大增益。综合考虑选取虚拟电感的值为1 mH。

4 仿真与实验验证

4.1 仿真分析

在Matlab/Simulink中搭建了基于VSG的微网逆变器控制模型，逆变器参数如表1所示。

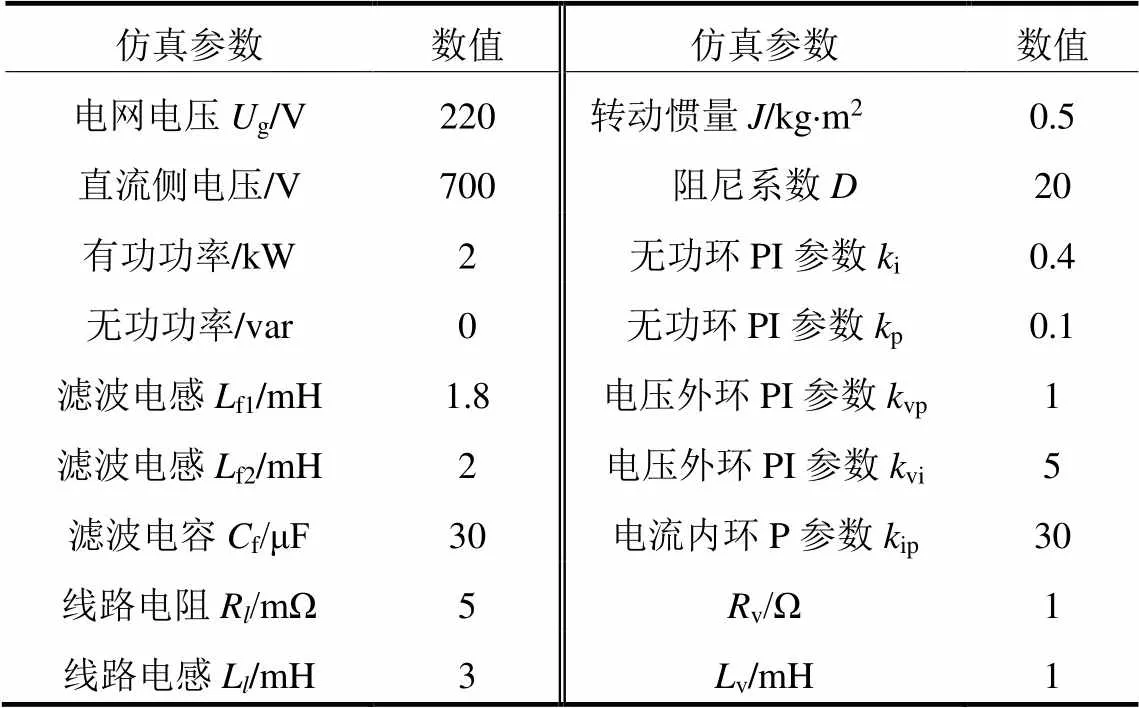
表1 仿真参数

在未加抑制策略前，VSG输出电流产生畸变，如图11(a)；输出有功功率与无功功率在电网频率处发生振荡如图11(b)、图11(c)所示，且通过对有功功率与无功功率傅里叶分析可以看出，两者振荡的频率均为50 Hz。与前面理论分析一致。

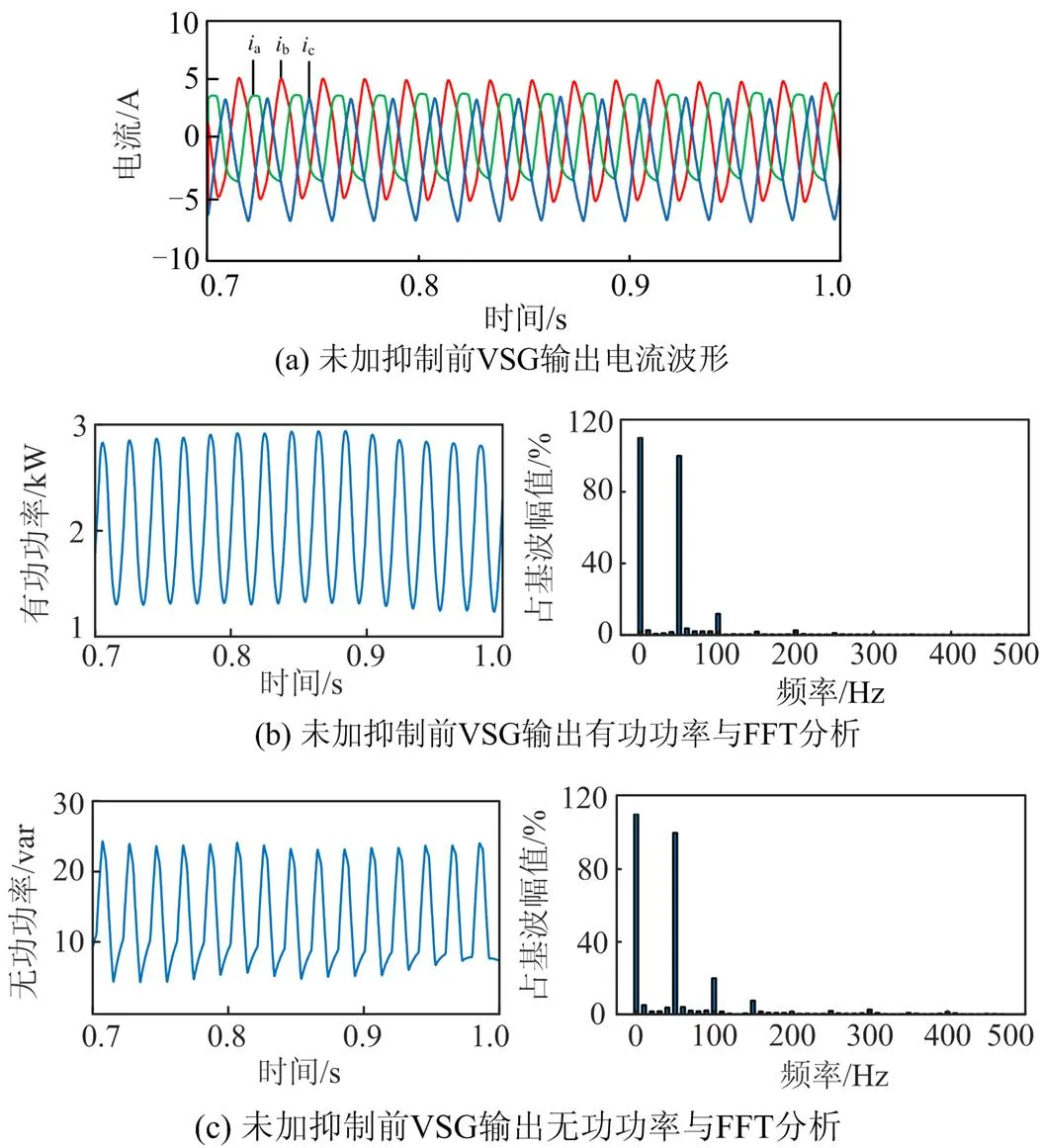
图11 未施加抑制策略前VSG输出电流与功率分析

在电压电流环引入虚拟复阻抗(v=1 Ω,v= 1 mH)之后，可以看到三相电流波形正弦度良好且三相对称，电流畸变完全被抑制，如图12(a)所示。另外为了验证阻抗参数对输出功率的影响，选取了两个不同的虚拟电阻值。图12(b)和图12(d)分别为v为0.2 Ω时系统输出的有功与无功功率，图12(c)和图12(e)分别为v为1 Ω时系统输出的有功与无功功率。通过不同阻值下的系统输出功率对比可以发现，选取v为0.2 Ω时振荡呈现衰减趋势，大约10个周期振荡才逐渐稳定，当选取v为1 Ω时，功率基本无振荡，且稳定速度也优于前者。

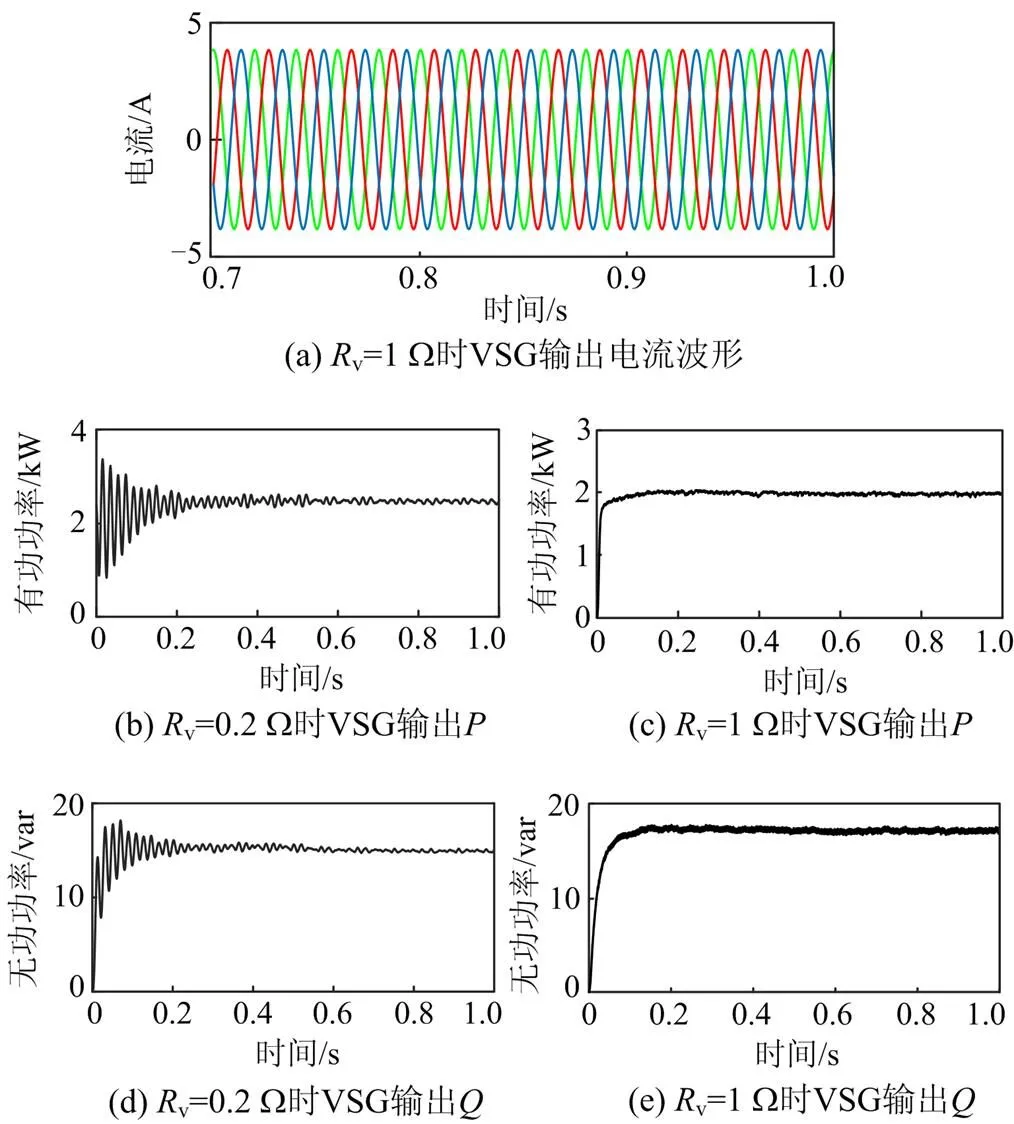
图12 施加抑制策略后VSG输出电流与功率波形

4.2 实验验证

为验证所提抑制策略的有效性，在实验室中搭建了一台并网逆变器实验样机，为了减小实验复杂度，直流侧采用稳压直流源，控制器采用TI公司的TMS320F28335，功率开关器件为Infineon公司的IGBT模块，驱动电路采用Avago公司的HCPL-316J光耦驱动芯片，利用上位机对系统进行监控。实验参数如表2所示。

实验硬件电路整体控制图如图13所示。

图 14(a)给出了在未加抑制策略时系统输出的电流、功率实验波形，可以看到逆变器输出的三相交流电流每一相都出现了畸变，其中A相电流幅值明显低于B、C两相，系统输出呈现不平衡；对于输出功率，有功功率与无功功率振荡周期都约为20 ms，振荡频率接近工频，实验结果与仿真结果基本吻合。而在引入复阻抗后输出波形如图14(b)所示，VSG输出电流波形得到修正，电流的畸变明显减小，电流平衡度良好；观察图14(b)，系统输出功率基本平稳，工频振荡基本被抑制。

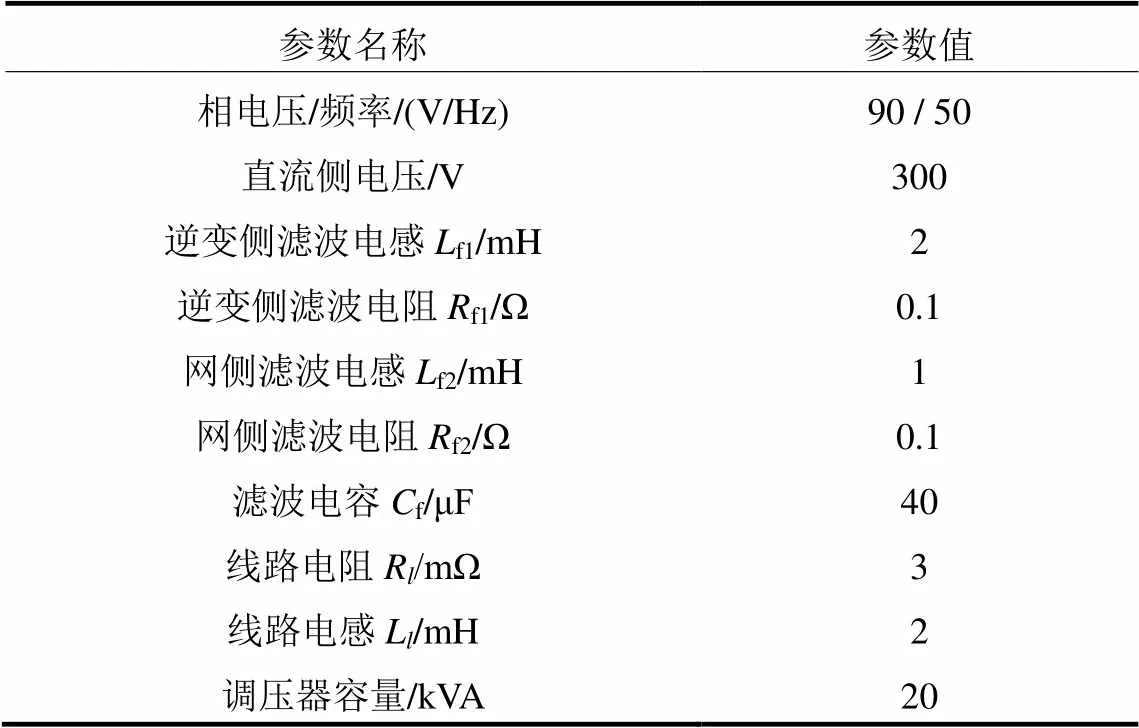
表2 实验参数

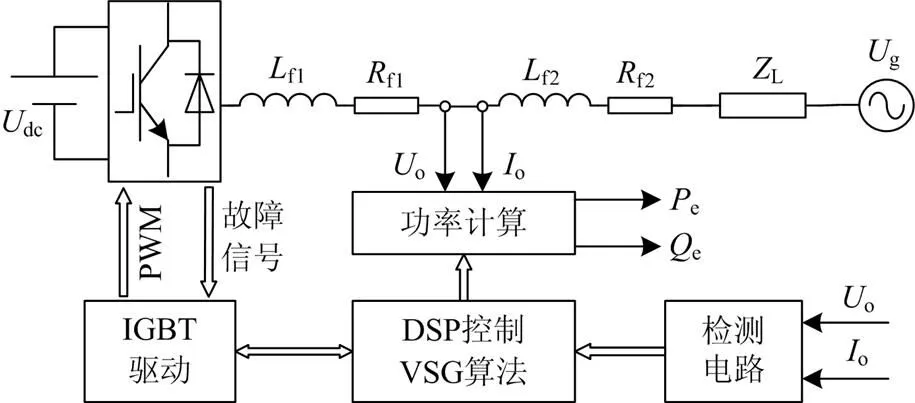
图13 硬件电路整体控制结构

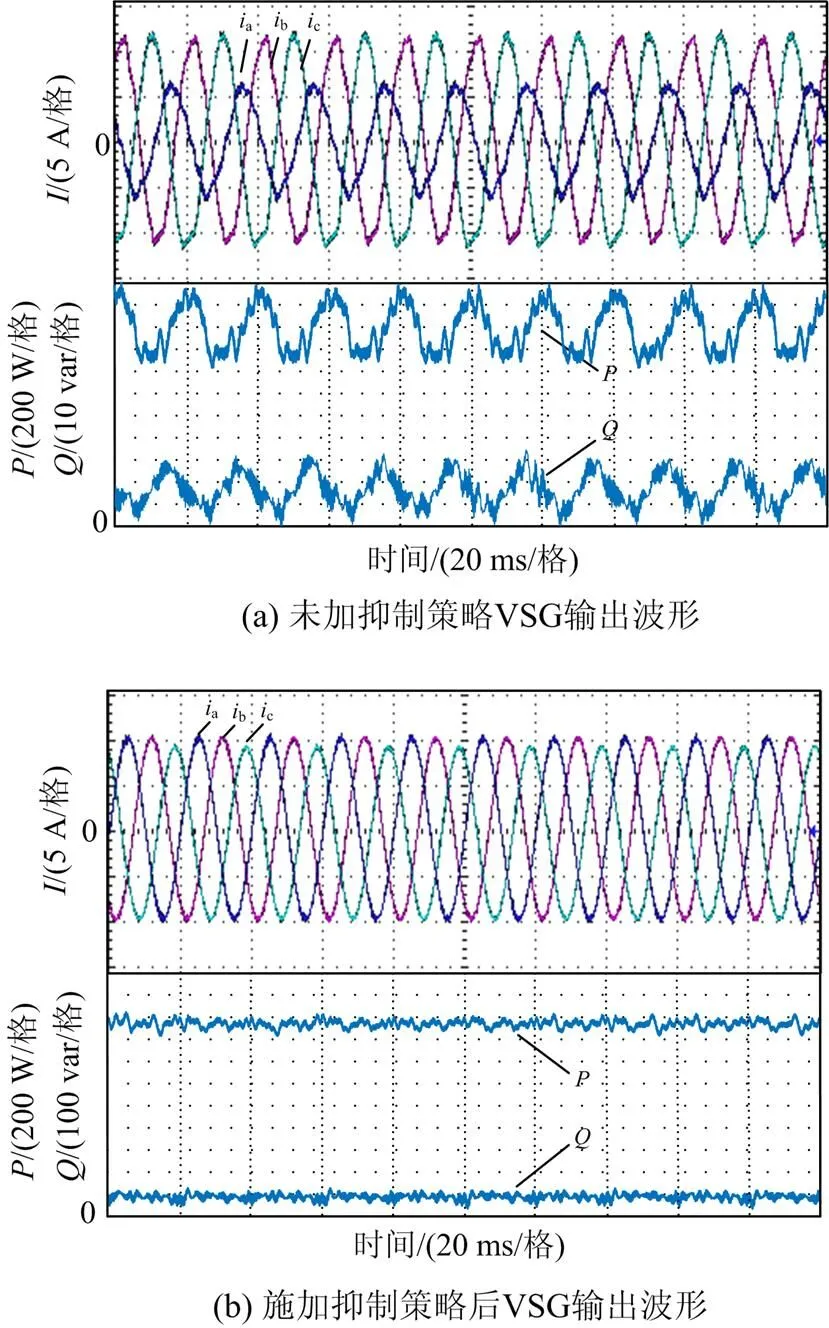
图14 虚拟复阻抗引入前后系统输出量比较

图15给出了系统在引入阻尼抑制策略后的A相输出电压与电流波形以及两者的FFT分析，可以看到此时输出电压与电流保持同相且谐波畸变率符合国家规定标准。据此，通过实验与仿真两方面验证，均体现出所提策略对抑制功率工频振荡具有有效性。

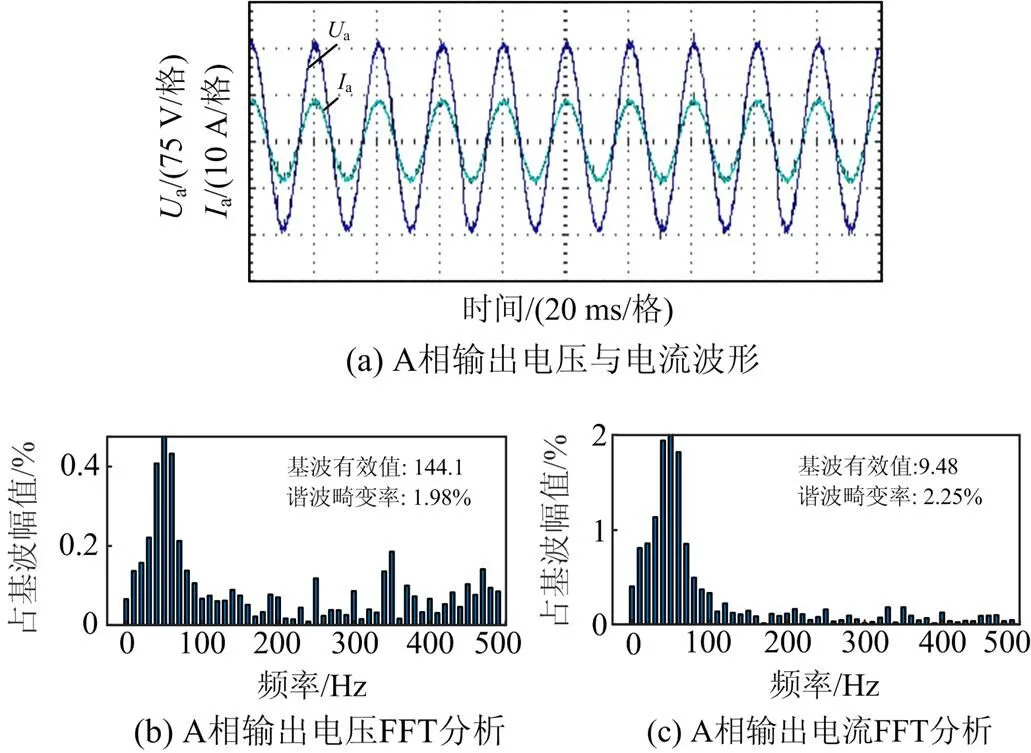
图15 系统A相输出电压与电流及谐波分析

5 结论

本文采用一种基于虚拟复阻抗的功率工频振荡抑制策略，定性分析了引入策略前后对系统输出功率的影响，得到如下结论。

1) 在传统VSG控制的微电网系统，系统输出总阻抗往往呈偏感性，在系统处于动态过程下容易导致系统输出功率发生工频振荡、电流失衡等问题。

2) 在电压电流双环控制环节，引入虚拟复阻抗可以实现重塑系统输出阻抗的目的，但是对于阻抗参数的选取需要根据系统的实际条件而定。

3) 通过Simulink仿真与实验平台的验证，可以证明在VSG控制下的微网系统会产生工频振荡现象；在引入虚拟复阻抗之后，振荡现象可以被抑制，证明了所提算法的有效性。

[1] 董凌, 李延和, 刘锋, 等. 区域全清洁能源供电的发展路径与实践—以青海省为例[J]. 全球能源互联网, 2020, 3(4): 385-392.

DONG Ling, LI Yanhe, LIU Feng, et al. Development path and practice of regional fully clean power supply: a case study of Qinghai province[J]. Journal of Global Energy Interconnection, 2020, 3(4): 385-392.

[2] 范坤乐, 杨承, 王平, 等. 高比例新能源渗透下天然气发电装机容量分配研究[J]. 广东电力, 2020, 33(1): 1-8.

FAN Kunle, YANG Cheng, WANG Ping, et al. Study on capacity allocation for gas-fired power generation units based on high penetration of renewable energy[J]. Guangdong Electric Power, 2020, 33(1): 1-8.

[3] 沈珺, 柳伟, 李虎成, 等. 基于强化学习的多微电网分布式二次优化控制[J]. 电力系统自动化, 2020, 44(5): 198-206.

SHEN Jun, LIU Wei, LI Hucheng, et al. Reinforcement learning based distributed secondary optimal control for multiple microgrids[J]. Automation of Electric Power Systems, 2020, 44(5): 198-206.

[4] OLUJOBI O J. The legal sustainability of energy substitution in Nigeria's electric power sector: renewable energy as alternative[J]. Protection and Control of Modern Power Systems, 2020, 5(4): 358-369.

[5] 张宇涵, 杜贵平, 雷雁雄, 等. 直流微网混合储能系统控制策略现状及展望[J]. 电力系统保护与控制, 2021, 49(3): 177-188.

ZHANG Yuhan, DU Guiping, LEI Yanxiong, et al. Current status and prospects of control strategy for a DC micro grid hybrid energy storage system[J]. Power System Protection and Control, 2021, 49(3): 177-188.

[6] 张明锐, 王俊凯, 王佳莹, 等. 微网混合式孤岛检测及运行模式切换研究[J]. 电力系统保护与控制, 2020, 48(2): 1-8.

ZHANG Mingrui, WANG Junkai, WANG Jiaying, et al. Study on hybrid islanding detection and operation mode transition of microgrid[J]. Power System Protection and Control, 2020, 48(2): 1-8.

[7] EMAD G M, MOHAMED A, SHABIB G, et al. Microgrid dynamic security considering high penetration of renewable energy[J]. Protection and Control of Modern Power Systems, 2018, 3(3): 236-246.

[8] 孙大卫, 刘辉, 吴林林, 等. 虚拟同步发电机对低频振荡的影响建模与特性分析[J]. 电力系统自动化, 2020, 44(24): 134-144.

SUN Dawei, LIU Hui, WU Linlin, et al. Modeling and characteristic analysis on influence of virtual synchronous generator on low-frequency oscillation[J]. Automation of Electric Power Systems, 2020, 44(24): 134-144.

[9] 丁明, 杨向真, 苏建徽. 基于虚拟同步发电机思想的微电网逆变电源控制策略[J]. 电力系统自动化, 2009, 33(8): 89-94.

DING Ming, YANG Xiangzhen, SU Jianhui. Control strategy of micro-grid inverter based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2009, 33(8): 89-94.

[10] ZHONG Q, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[11]张兴, 朱德斌, 徐海珍. 分布式发电中的虚拟同步发电机技术[J]. 电源学报, 2012, 10(3): 1-6, 12.

ZHANG Xing, ZHU Debin, XU Haizhen. Review of virtual synchronous generator technology in distributed generation[J]. Journal of Power Supply, 2012, 10(3): 1-6, 12.

[12]朱慧敏, 苑舜. 基于功率解耦控制的虚拟同步发电机功率振荡抑制策略[J]. 智慧电力, 2020, 48(4): 70-76.

ZHU Huimin, YUAN Shun. Power oscillation suppression strategy of virtual synchronous generator based on power decoupling control[J]. Smart Power, 2020, 48(4): 70-76.

[13] 吕志鹏, 盛万兴, 钟庆昌, 等. 虚拟同步发电机及其在微电网中的应用[J]. 中国电机工程学报, 2014, 34(16): 2591-2603.

LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its application in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.

[14] 侍乔明, 王刚, 付立军, 等. 基于虚拟同步发电机原理的模拟同步发电机设计方法[J]. 电网技术, 2015, 39(3): 783-790.

SHI Qiaoming, WANG Gang, FU Lijun, et al. A design method of simulative synchronous generator based on virtual synchronous generator theory[J]. Power System Technology, 2015, 39(3):783-790.

[15] BABAYOMI O, LI Z, ZHANG Z. Distributed secondary frequency and voltage control of parallel-connected VSCS in microgrids: a predictive VSG-based solution[J]. Transactions on Power Electronics and Applications, 2020, 5(4): 342-351.

[16]那广宇, 王亮, 刘雨桐, 等. 基于VSG的改进型虚拟阻尼控制策略与特性分析[J]. 智慧电力, 2020, 48(4): 48-54.

NA Guangyu, WANG Liang, LIU Yutong, et al. VSG based improved virtual damping control strategy and characteristics analysis[J]. Smart Power, 2020, 48(4): 48-54.

[17] 周建萍, 胡成奕, 茅大钧, 等. 基于模糊控制的自适应虚拟同步发电机控制策略[J]. 广东电力, 2020, 33(1): 53-60.

ZHOU Jianping, HU Chengyi, MAO Dajun, et al. Adaptive virtual synchronous generator control strategy based on fuzzy control[J]. Guangdong Electric Power, 2020, 33(1): 53-60.

[18] RAGHAVAN S V, JAYABARATHI R. Simulation and analysis of power synchronization control for voltage source inverter[C] // 2017 Recent Developments in Control, Automation & Power Engineering (RDCAPE), October 26-27, 2017, Noida, India: 348-353.

[19] ZHANG L, NEE H, HARNEFORS L. Analysis of stability limitations of a VSC-HVDC link using power-synchronization control[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1326-1337.

[20] 单碧涵, 王宝华, 刘洋, 等. 基于定子侧模拟电阻的双馈风电场次同步振荡抑制策略研究[J]. 电力系统保护与控制, 2020, 48(5): 10-16.

SHAN Bihan, WANG Baohua, LIU Yang, et al. Research on subsynchronous oscillation suppression strategy of doubly-fed wind farm based on stator side analog resistance[J]. Power System Protection and Control, 2020, 48(5): 10-16.

[21] LI Y, FAN L, MIAO Z. Wind in weak grids: low-frequency oscillations, subsynchronous oscillations, and torsional interactions[J]. IEEE Transactions on Power Systems, 2020, 35(1): 109-118.

[22] 王杨, 张兴, 郭梓暄, 等. 虚拟同步发电机次同步振荡抑制策略[J]. 电力电子技术, 2021, 55(4): 20-25.

WANG Yang, ZHANG Xing, GUO Zixuan, et al. Suppression strategy of subsynchronous oscillation of virtual synchronous generator[J]. Power Electronics, 2021, 55(4): 20-25.

[23] 邢华栋, 张叔禹, 尹柏清, 等. 风电并网系统次同步振荡稳定性分析与控制方法研究综述[J]. 电测与仪表, 2020, 57(24): 13-21.

XING Huadong, ZHANG Shuyu, YIN Baiqing, et al. Review of sub-synchronous oscillation stability analysis and control method for grid-connected wind power system[J]. Electrical Measurement & Instrumentation, 2020, 57(24): 13-21.

[24] 高志强, 李松, 周雪松, 等. 线性自抗扰在光伏发电系统MPPT中的应用[J]. 电力系统保护与控制, 2018, 46(15): 52-59.

GAO Zhiqiang, LI Song, ZHOU Xuesong, et al. Application of linear active disturbance rejection in MPPT of photovoltaic power generation system[J]. Power System Protection and Control, 2018, 46(15): 52-59.

[25] 杜燕, 崔林波, 杨向真, 等. 并网逆变器的阻抗自适应控制方法[J]. 电力系统自动化, 2018, 42(6): 120-127.

DU Yan, CUI Linbo, YANG Xiangzhen, et al. Adaptive control method of impedance for grid-connected inverters[J]. Automation of Electric Power Systems, 2018, 42(6): 120-127.

[26] 曾正, 赵荣祥, 吕志鹏, 等. 光伏并网逆变器的阻抗重塑与谐波谐振抑制[J]. 中国电机工程学报, 2014, 34(27): 4547-4558.

ZENG Zheng, ZHAO Rongxiang, LÜ Zhipeng, et al. Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems[J]. Proceedings of the CSEE, 2014, 34(27): 4547-4558.

[27] 王金华, 王宇翔, 顾云杰, 等. 基于虚拟同步发电机控制的并网变流器同步频率谐振机理研究[J]. 电源学报, 2016, 14(2): 17-23.

WANG Jinhua, WANG Yuxiang, GU Yunjie, et al. Synchronous frequency resonance in grid-connected VSCs with virtual synchronous generator technology[J]. Journal of Power Supply, 2016, 14(2): 17-23.

[28] 李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-391.

LI Wuhua, WANG Jinhua, YANG Heya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391.

[29] 李新, 肖龙, 刘国梁, 等. 基于相位补偿和交叉前馈补偿的VSG功率振荡抑制策略[J]. 浙江大学学报(工学版), 2018, 52(3): 569-576.

LI Xin, XIAO Long, LIU Guoliang, et al. VSG power oscillation suppression strategies based on phase compensation and cross feedforward compensation[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(3): 569-576.

[30] 张庆海, 罗安, 陈燕东, 等. 并联逆变器输出阻抗分析及电压控制策略[J]. 电工技术学报, 2014, 29(6): 98-105.

ZHANG Qinghai, LUO An, CHEN Yandong, et al. Analysis of output impedance for parallel inverters and voltage control strategy[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 98-105.

Power frequency oscillation of a microgrid inverter based on VSG control

MA Ye, SHI Liping, LI Heng, LI Hao, SUN Yifeng, MIAO Rongxin

(School of Electrical and Power Engineering, China University of Mining and Technology, Xuzhou 221008, China)

Distributed generation mostly uses a power electronic converter as interface to interact with the power grid. Virtual synchronous generator (VSG) control technology has become a new scheme of inverter control because of its excellent internal and external performance in simulating a traditional synchronous generator. However, it is easy to excite the current transient process of the line inductance in fast-moving power electronic devices, and this will have adverse effects on the system.Considering the transient process of line inductance, a dynamic small signal model of system output power is established. From the model, the reason for oscillation is related to the output impedance of the system.In this paper, a new damping control strategy is adopted. By introducing virtual complex impedance into the voltage outer loop, the impedance characteristics of the system can be reshaped and the power oscillation can be suppressed. Both simulation and experiment verify the power frequency oscillation in VSG and the effectiveness of the proposed control strategy.

VSG; dynamic small signal model; power frequency oscillation; virtual complex impedance

10.19783/j.cnki.pspc.210306

国家自然科学基金面上项目资助(62076243)

This work is supported by the National Natural Science Foundation of China (No. 62076243).

2021-03-23；

2021-06-22

马 也(1996—)，男，通信作者，硕士研究生，主要研究方向为微网逆变器并网运行；E-mail: 1572213599@qq.com

史丽萍(1964—)，女，博士，教授，研究方向为煤矿机电设备及其自动化、电力电子在电力系统中的应用、设备与电网运行及故障诊断等。E-mail: shiliping98@126.com

(编辑 周金梅)