基于下垂控制的单台换流器-无穷大系统数学模型及直流系统稳定的解析条件
陈建新,张 旭,孟浩杰,徐寅飞,任新卓,邓小电,李宇骏
基于下垂控制的单台换流器-无穷大系统数学模型及直流系统稳定的解析条件
陈建新1,张 旭2,孟浩杰1,徐寅飞1,任新卓1,邓小电1,李宇骏2
(1.杭州电力设备制造有限公司,浙江 杭州 310018;2.西安交通大学电气工程学院,陕西 西安 710049)
基于功率-电压下垂控制的换流器因其较好的控制灵活性在多端直流输电系统中的应用日益广泛,同时也为直流电网稳定运行带来了新的挑战。利用单输入单输出分析法研究了单台并网换流器直流系统的稳定性问题。首先,建立系统扰动后的直流电压变化量和直流电流变化量间的传递函数。其次,利用Routh判据得到不同控制模式下系统的稳定判据。然后,定义了一个评价系统稳定性的关键指标—直流功率传输极限。最后,数值仿真结果验证了稳定性分析的准确性,以及所提稳定判据的正确性。
基于功率-电压下垂控制换流器;直流侧稳定性;单输入单输出;Routh判据;直流功率传输极限
0 引言
基于功率-电压下垂控制的换流器具有较高的可靠性和控制灵活性,其在多端直流输电系统(Multi-terminal DC, MTDC)中的应用日益广泛[1-2]。为保障多端直流输电系统的稳定运行,有必要研究并网换流器的控制作用对多端直流输电系统稳定性的影响。已有文献详细介绍了应用于多模块多电平换流器的控制策略[3-5],及并网换流器的控制作用对交流系统稳定性的影响[6-10],发现重载场景下以及不合适的锁相环控制参数会导致系统失稳[7-9],并针对现有控制策略存在的不足,提出了对应的改进方案[11-14]。文献[10]提出了一种含阻尼控制的附加有功控制策略,能够消除直流电压和输出有功功率的偏移。文献[12-13]提出了分散接入式混合直流系统的机电暂态建模方法和控制策略以提升其在交流故障下的运行特性。然而,鲜有文献分析研究换流器直流系统的稳定性问题。因此,本文将着重研究并网换流器的控制作用对直流系统稳定性的影响。
目前,用于分析直流系统稳定性的方法主要有两类:模态分析法和基于阻抗模型的分析法(Impedance-Based Analysis, IMA)。前者是将直流电网数学模型写成统一的状态空间表达,通过求解矩阵特征值来分析系统的稳定性[15]。该方法的主要优势在于可以分析系统在若干关键运行状态下的稳定性。同时,利用从该分析法中获得的参与因子可识别出与主导特征值有关的状态变量,找出影响稳定性的主要因素,并优化系统的控制策略[16-19]。但模态分析法过度依赖复杂的数值计算,无法对系统失稳的机理做出物理解释,且基于模态分析得到的稳定性判据无法给出影响系统的关键参数。后者需要分别求解两个串联子系统的阻抗,两个子系统的阻抗比若满足Nyquist稳定性判据,那么整个系统便能保持稳定[20]。文献[21-22]分别导出了换流器直流系统和交流系统的阻抗表达式。文献[23-24]利用阻抗法研究了两端基于电压源型换流器的高压直流输电(VSC-HVDC)系统的稳定性,并指出当电压源型换流器表现出负阻尼特性时,系统可能会失稳。文献[25-26]通过阻抗分析表明,若换流器的下垂控制参数设置不当,将给系统引入负阻尼,进而导致系统失稳。文献[27]引入了多输入多输出(MIMO)系统的相对增益阵列(RGA),并较好地评价了换流器间的相互作用。但阻抗法无法得到保证系统稳定的各参数间满足的解析关系,导出系统稳定的充分条件,得到稳定性判据。
本文采用单输入单输出(Single Input Single Output, SISO)分析法研究并网换流器的控制作用对直流系统稳定性的影响。首先建立单台换流器-无穷大系统的数学模型,推导选定的输入量与输出量之间的传递函数,基于Routh判据,得到控制器参数与系统稳定间的数学关系,导出系统稳定的充分必要条件。最后,基于PSCAD/EMTDC的仿真分析验证了所提稳定判据的正确性。
1 单台换流器-无穷大系统数学模型
1.1 换流器数学模型
换流器模型包括系统模型与控制模型,阶数较高,对研究并网换流器的控制作用对直流系统稳定性的影响带来诸多不便。因此,本文忽略换流器锁相环与内环电流控制的动态过程,同时认为交流系统理想,从而得到用于分析直流系统稳定性的换流器简化模型。
两电平电压源型换流器的直流系统等效电路如图1所示。换流器直流系统的动态过程为
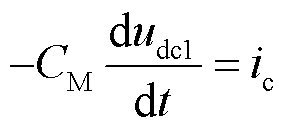
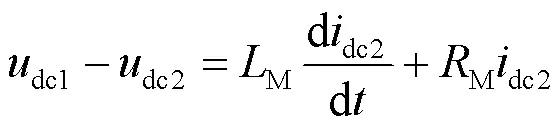
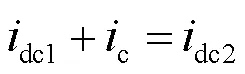
式中:M是换流器直流母线电容;M和M分别是直流线路的等效电感和等效电阻;dc1dc2分别是电容电压和系统受端的直流电压;c是电容电流;dc1是交流系统馈入电流;dc2是线路上传输的直流电流。
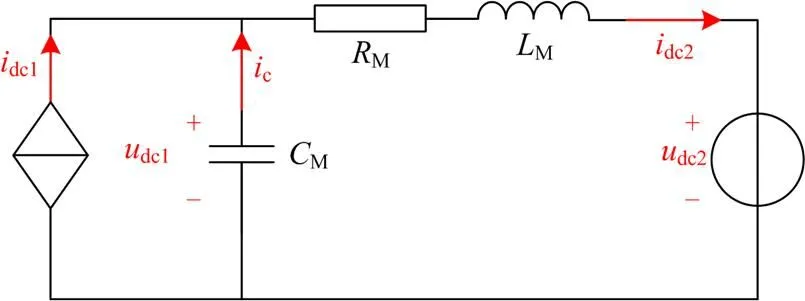
图1 换流器直流侧等效电路图
在传统的主从控制策略下,直流电网只有一端控制直流电压,其余端口调控各自的传输功率。一旦维持直流母线电压的主换流器退出运行,多端直流输电系统便会崩溃。而在功率-电压下垂控制策略下,所有端口按照下垂系数自动分配功率,提高了系统的可靠性,因而在直流电网中具有更广阔的应用前景[28-29]。功率-电压下垂控制策略如图2,数学表达式为
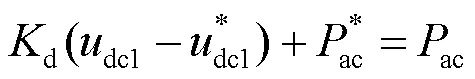
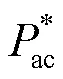
图2 换流器下垂控制框图
Fig. 2 Power-voltage droop-based control for two-level VSC
忽略换流阀的开关损耗,换流器的交、直流系统间传输的有功功率应保持平衡。

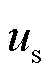
将式(5)代入式(4),控制方程可写为
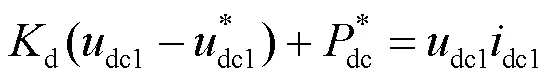
由式(1)—式(6)描述的换流器原始方程和控制方程构成用于分析单台换流器-无穷大系统稳定性的换流器数学模型。
1.2 传递函数的建立
根据上述建立的换流器数学模型,可以建立单台换流器-无穷大系统的小干扰分析模型,通过选择合适的输入量和输出量,建立它们之间的传递函数关系,进而得到系统的特征方程。
将系统方程在稳态运行点处线性化,得到小扰动形式的数学模型为
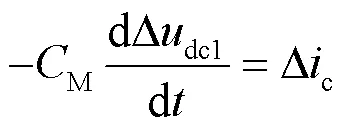



对式(7)—式(10)进行Laplace变换,写成小扰动形式下的频域方程。其频域等效电路如图3所示。

图3 换流器频域等效电路图

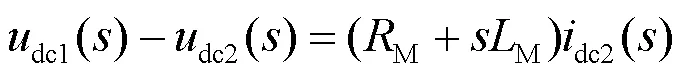
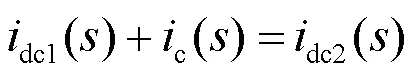



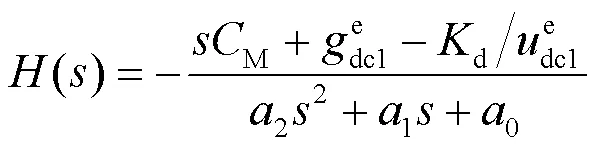
其中,
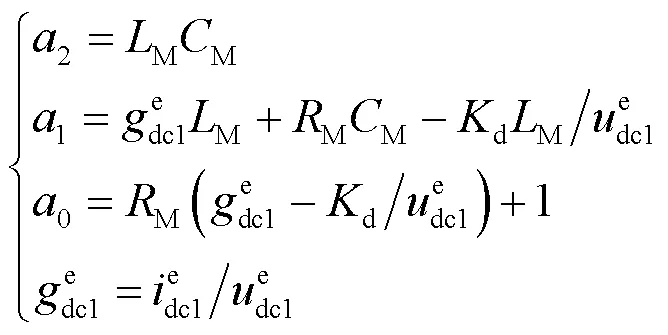
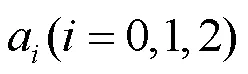
式(17)和式(18)描述的是系统受扰后直流电流变化量与直流电压变化量间的传递函数。基于此传递函数,利用相关的复频域分析方法,分析单台换流器-无穷大系统的稳定性,导出系统稳定的充分必要条件,进而得到系统的稳定判据。
2 单换流器-无穷大系统的稳定性分析
2.1 系统稳定的充分必要条件
本节基于经典的Routh判据,对单台换流器-无穷大系统的小干扰稳定性进行研究,导出系统稳定的充分必要条件。
由式(17)和式(18)表示的系统传递函数可以得到系统的特征多项式:
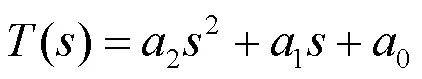
其中,
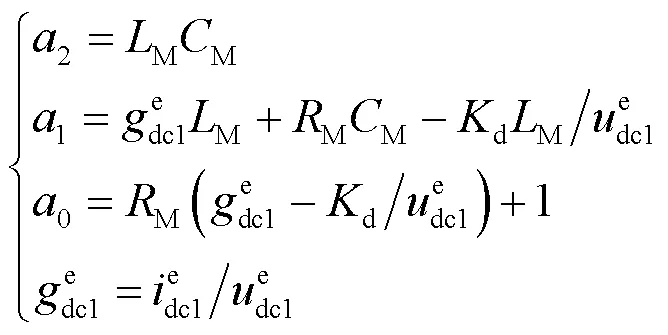
根据经典两阶线性系统的Routh判据,可以列出特征多项式()的Routh阵列。
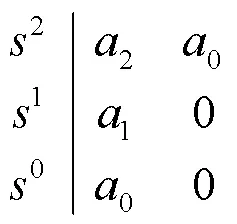

2.2 参数灵敏度分析
由式(22)可以看出,影响系统稳定的电气参数和控制参数较多且关系复杂。为了找出影响系统稳定性的主要因素,需要对式(22)中的各参数进行灵敏度分析。
根据二阶线性系统的阻尼系数的定义,通过式(19)和式(20)可以求得该系统的阻尼系数,具体表达如下:
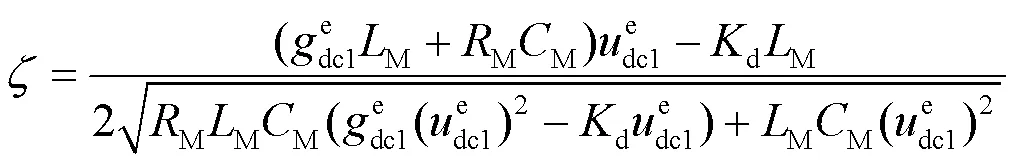
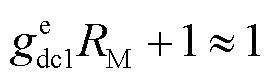
将式(24)代入式(23)中,可以得到系统近似的阻尼系数的表达式,如式(25)。

为了评价各参数对阻尼系数的贡献程度,计算式(25)中出现的各参数的灵敏度,具体结果如下:
参数M的灵敏度为
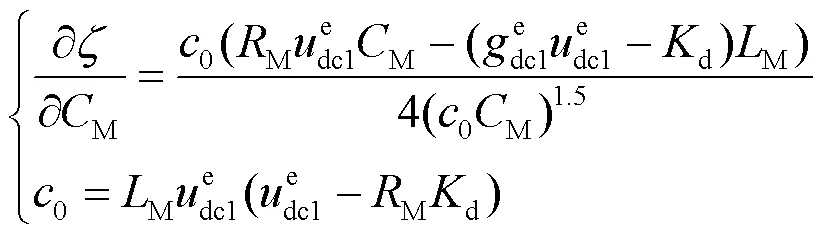
参数M的灵敏度为

其中,
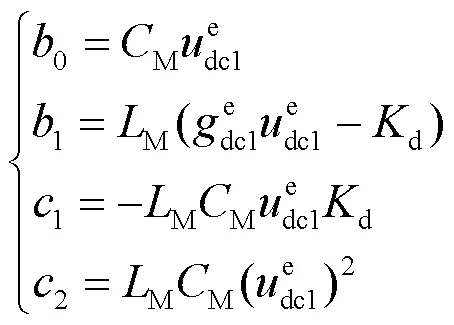
参数d的灵敏度为
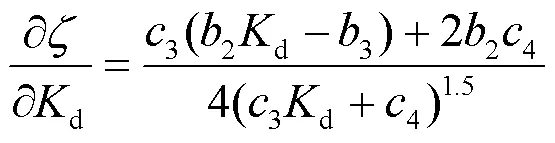
其中,

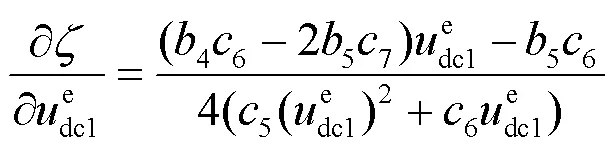
其中,

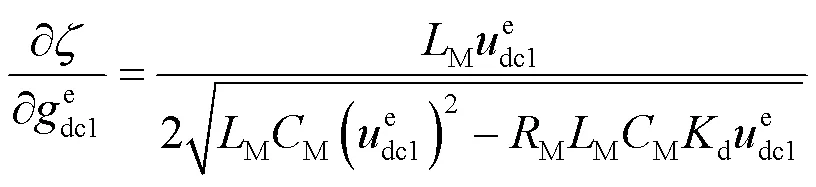
参数M的灵敏度为

对式(26)—式(34)进行分析,可知各参数灵敏度公式的分母是相同的,故只考察分子的正负即可判断各参数对系统稳定性的贡献程度。在实际的高压直流输电工程中的典型电气参数和控制参数代入以上式子中估算后,可以得出以下结论:
1) 增加换流器直流母线电容值有利于系统稳定;
2) 增加线路额定电流与额定电压的比值有利于系统稳定;
3) 增加线路电阻值有利于系统稳定;
4) 增加线路电感值不利于系统稳定;
5) 增加输电线路的额定电压有利于系统稳定;
6) 当下垂控制参数在规定的取值范围内时,下垂控制参数取值越小越有利于系统稳定。
综合以上分析,可以得出:下垂控制参数d对系统稳定性影响最大,且如果设置不当,极有可能会给系统引入负阻尼从而导致系统失稳;其余参数对于系统稳定性的影响相对较小。所以本文将对不同d取值下的系统稳定性进行讨论。
3 不同控制模式下系统的稳定性分析
3.1 定有功功率控制模式
当下垂控制参数d等于0时,换流器处于定有功功率控制模式。此时系统稳定的充分必要条件可改写为



由于直流系统传输线的电阻值通常较小,所以在定有功功率控制模式下,始终满足式(37)的不等关系。
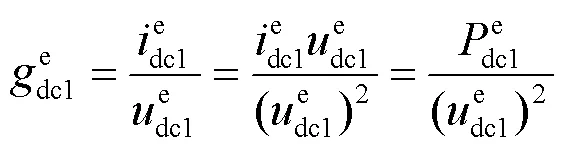
将式(38)代入式(36)并进行相应的数学变换,得到并网换流器的稳定域。具体表达为

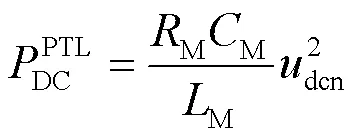
式中,dcn是直流线路的额定电压。
综上所述,在定有功功率控制模式下,只要系统中传输的有功功率不超过系统的直流功率传输极限,系统将始终保持稳定。
3.2 定电压控制模式
当下垂控制参数d选取一个足够大的负数时,换流器处于定电压控制模式。此时,式(22)中的两个不等式将满足式(41)。

由式(41)可知,当换流器处于定电压控制模式时,将始终满足系统稳定的充分必要条件,系统不存在稳定性问题。
综上所述,在定电压控制模式下,系统将始终保持稳定,不存在稳定性问题。
3.3下垂控制模式
当下垂控制参数d的取值处于负无穷大和零之间时,式(22)为系统稳定的充分必要条件。由式(22)求出下垂控制参数的取值范围:

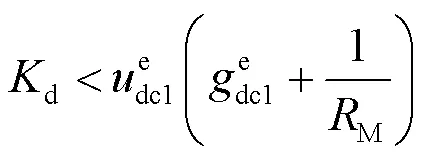
由于直流输电系统的传输线的电阻值通常较小,式(43)的不等关系是始终成立的。所以下垂控制参数d只要满足式(42)的不等关系,系统就能保持稳定。
特别地,若要求系统在任意工况下始终处于稳定状态,d必须满足以下条件:无论d取何值,式(42)的不等关系始终成立。由此可推导出系统稳定的充分条件为


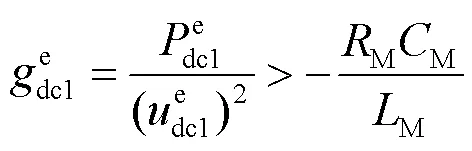
由式(46)可以解得系统的稳定域,具体为

式(47)所得稳定域结果与式(39)一致,两者所确定的直流功率传输极限也是一致的,这里不再赘述。
综上所述,当换流器处于下垂控制模式时,保证系统稳定的d取值与换流器的初始工作状态有关。若换流器工作在整流状态,式(42)的不等关系恒成立,系统始终保持稳定;若换流器工作在逆变状态,此时系统是否稳定取决于架空线上传输的有功功率的大小。若传输的有功功率不超过系统的直流功率传输极限,系统参数将始终满足式(45)的不等关系,系统不会出现稳定性问题;若传输的有功功率超过系统的直流功率传输极限,当下垂控制参数d满足式(42)的不等关系时,系统保持稳定,否则,系统失稳。
4 数值仿真结果
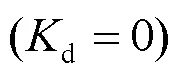
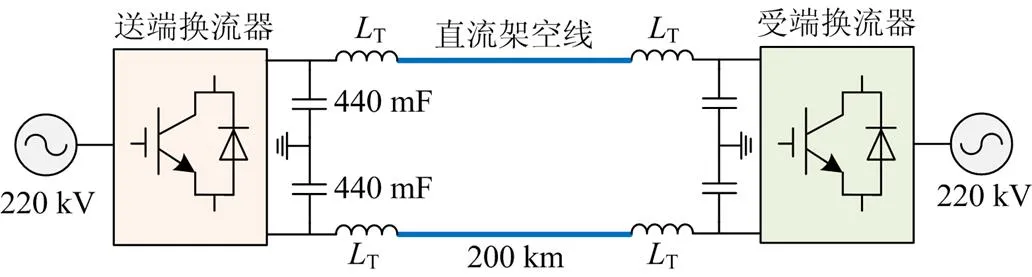
图4 VSC-HVDC系统仿真模型图
4.1送端换流器的参考功率对换流器直流系统稳定性的影响
图5为两端VSC-HVDC系统在传输功率变化时的动态过程。根据上述分析,当送端换流器工作在逆变状态且传输有功功率较高时,高压直流输电系统可能会失稳。在本次仿真中,送端换流器初始输送的有功功率设置为-100 MW,负号表示送端换流器工作在逆变状态。图5(a)和图5(b)分别为当送端换流器的参考功率突然发生变化时,直流电流和直流功率的动态响应。随着输送的有功功率的增加,直流电流和直流功率的振荡逐渐明显。当输送的功率达到-350 MW时,直流电流和直流功率均出现增幅振荡现象,系统的阻尼比为负数(-0.012 0),说明此时系统已经失稳。为了找出换流器工作在逆变状态时系统的直流功率传输极限,当送端换流器的参考功率以60 MW/s的速度减小时,换流器实际传输的有功功率的变化过程如图5(c)所示。可以发现,当送端换流器输送的功率达到247.31 MW时,流经换流器的有功功率开始出现增幅振荡。由此可以确定系统的直流功率传输极限是247.31 MW。由图5(c)进一步发现,因实际的电压源型换流器所采用的快速电流控制存在饱和,所以在经过12 s之后会出现等幅振荡现象。
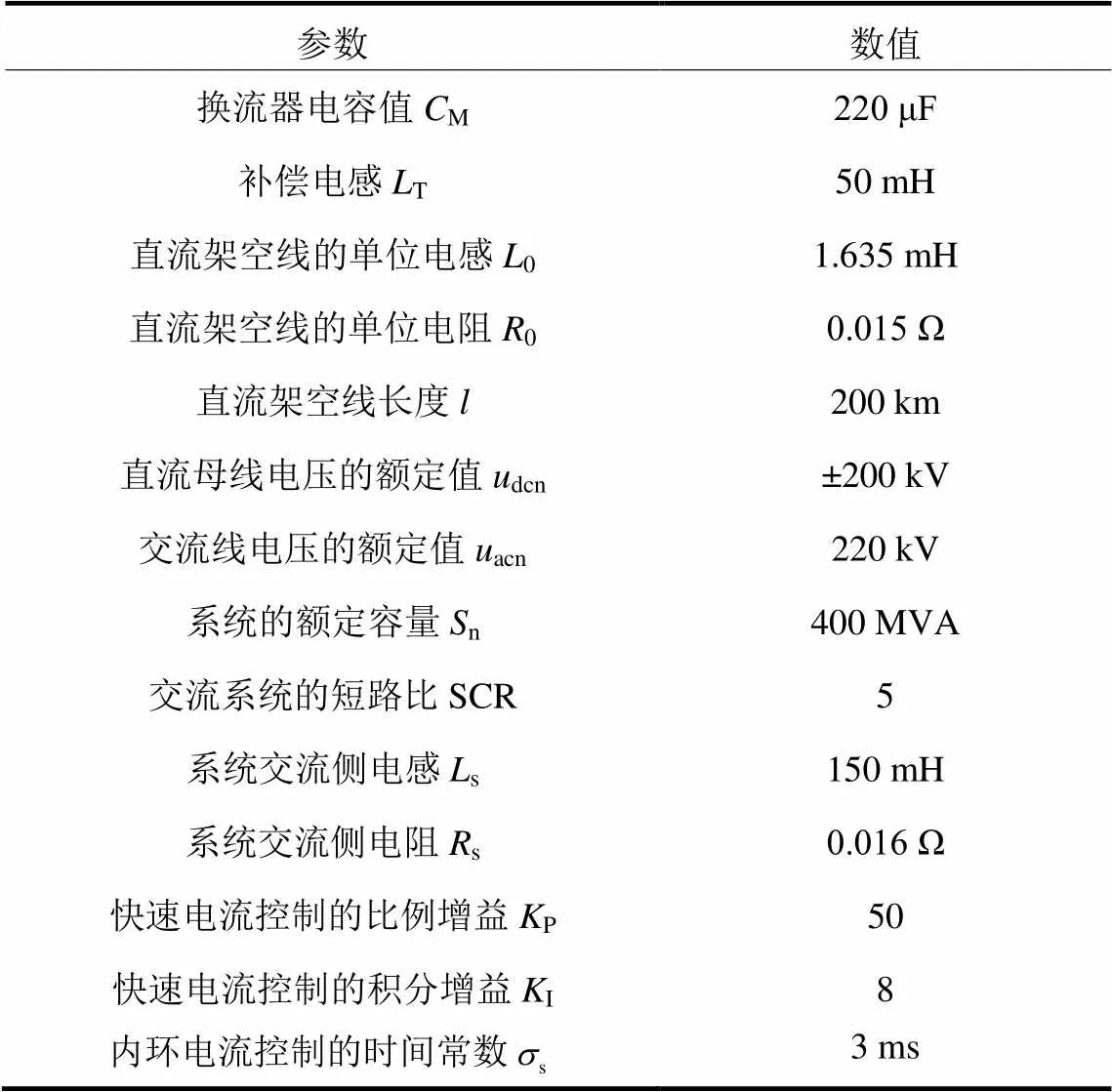
表1 测试用高压直流输电系统的相关参数

图5不同送端换流器参考功率下VSC-HVDC系统的动态响应
4.2 不同电气参数对换流器直流系统稳定性的影响
不同参数对换流器直流系统稳定性的影响如图6所示。图6(a)—图6(d)分别讨论了换流器直流母线电容、直流架空线长度、直流补偿电感以及换流器的下垂控制参数对系统稳定性的影响。在本次仿真中,通过短时间内改变有功功率参考值来施加扰动。由图6(a)可以看出,若采用数值较小的换流器直流母线电容(50 μF),直流传输功率的振荡幅度会逐渐增加;同时,通过计算每种电容值对应的阻尼系数可以看出,随着采用的电容的数值逐渐增加,系统的动态性能得到较大的提升,系统振荡得到明显抑制。由图6(b)可以看出,通过增加直流架空线的长度的方式可以增加线路的电阻,能够较大幅度地提高主导模式下系统的阻尼,系统的振荡幅度也能得到有效的抑制。相反地,随着直流线路端口处安装的补偿电感数值的增加,系统的阻尼系数会迅速下降,对系统的稳定性产生不利影响。由图6(c)可以看出,若线路上安装较大的补偿电感,主导模式下系统的振荡频率会明显下降。图6(d)为不同下垂控制参数对换流器直流系统稳定性的影响。从图中可以看出:当下垂控制参数为正数时,系统输送的有功功率会出现明显的增幅振荡现象;相反,当采用负的下垂控制参数时,系统的动态性能会有很好的改善,此时系统的阻尼系数能达到0.042 3;同时系统的振荡会在1 s内快速衰减。

图6 不同参数对系统动态性能的影响
5 结论
本文着重研究了高压直流电网的换流器直流系统的稳定性问题,详细分析了换流器的外环电压控制作用对系统稳定性的影响。首先,建立了系统受扰后直流电压变化量和直流电流变化量间的传递函数。其次,根据所求得的传递函数,基于Routh判据导出了不同控制模式下系统的稳定性判据。研究发现:在定有功功率控制模式下,当换流器工作在逆变器状态时会向系统引入负阻尼;若直流网络中的阻尼无法抵消此负阻尼,系统将出现增幅振荡现象。此外,本文还定义了系统运行的稳定边界,即直流功率传输极限。当换流器工作在逆变状态时,若线路上传输的有功功率超出此阈值,系统振荡的幅度可能会增加。通过对各参数的灵敏度分析可知,为了改善系统的稳定性,可以适当增加换流器直流母线电容值,适当增加输电距离,尽量减少补偿电感值,并将下垂控制参数控制在一个合理的范围内。对于多端直流输电系统而言,其模型阶数较单换流器-无穷大系统将会增加,该系统具有更高阶的特征方程,难以使用Routh判据导出系统解析的稳定条件。为解决上述问题,今后将在本文研究的基础上考虑内环电流控制、电压-功率外环控制和锁相环控制对单台换流器-无穷大系统稳定性的影响,探索能够分析高阶线性系统稳定性的方法,并基于得到的稳定判据设计合适的控制器来保障直流输电系统的稳定。
[1] 蒋冠前, 李志勇, 杨慧霞, 等. 柔性直流输电系统拓扑结构研究综述[J]. 电力系统保护与控制, 2015, 43(15): 145-153.
JIANG Guanqian, LI Zhiyong, YANG Huixia, et al. Research review on topological structure of flexible HVDC system[J]. Power System Protection and Control, 2015, 43(15): 145-153.
[2] HE Jinwei, LI Yunwei, LIANG Beihua, et al. Inverse power factor droop control for decentralized power sharing in series-connected-microconverters-based islanding microgrids[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7444-7454.
[3] 蔡永梁, 任成林, 周竞宇, 等. 基于MMC的柔性直流输电电容电压波动抑制方法[J]. 电力系统保护与控制, 2017, 45(5): 45-50.
CAI Yongliang, REN Chenglin, ZHOU Jingyu, et al. Control strategy for suppressing capacitor voltage ripple of MMC-HVDC[J]. Power System Protection and Control, 2017, 45(5): 45-50.
[4] 杨兴武, 杨帆, 薛花, 等. 基于占空比调制的模块化多电平换流器模型预测控制[J]. 电力系统自动化, 2021, 45(17): 134-142.
YANG Xingwu, YANG Fan, XUE Hua, et al. Duty-cycle modulation based model predictive control of modular multilevel converter[J]. Automation of Electric Power Systems, 2021, 45(17):134-142.
[5] 张夏辉, 韩民晓, 杨景刚, 等. 直流侧电压波动对MMC的环流影响机理分析及抑制方法[J]. 电力系统自动化, 2021, 45(15): 122-131.
ZHANG Xiahui, HAN Minxiao, YANG Jingang, et al. Analysis on influence mechanism of DC-side voltage fluctuation on circulating current of modular multilevel converter and its suppression method[J]. Automation of Electric Power Systems, 2021, 45(15): 122-131.
[6] 丁江萍, 吕煜, 赵西贝, 等. 适用于架空线柔直的嵌套式全桥型混合MMC方案[J]. 中国电机工程学报, 2019, 39(23): 6844-6851, 7098.
DING Jiangping, LÜ Yu, ZHAO Xibei, et al. The embedded full-bridge type hybrid MMC suitable for overhead line VSC-HVDC transmission system[J]. Proceedings of the CSEE, 2019, 39(23): 6844-6851, 7098.
[7] WEN Bo, BOROYEVICH D, BURGOS R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[8] WANG Xiongfei, HARNEFORS L, BLAABJERG F. Unified impedance model of grid-connected voltage-source converters[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1775-1787.
[9] LU Dapeng, WANG Xiongfei, BLAABJERG F, Impedance-based analysis of DC-link voltage dynamics in voltage-source converters[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3973-3985.
[10] 董桓锋, 唐庚, 侯俊贤, 等. 海上风电接入多端柔性直流输电系统中换流站退出运行时直流功率再分配策略[J]. 电网技术, 2017, 41(5): 1398-1406.
DONG Huanfeng, TANG Geng, HOU Junxian, et al. Optimized power redistribution of VSC-MTDC transmission with offshore wind farms integrated after onshore converter outage[J]. Power System Technology, 2017, 41(5): 1398-1406.
[11]孙冰, 包丹, 张磊. 考虑惯性与阻尼特性的MMC-HVDC附加功率控制策略[J]. 电力系统保护与控制, 2020, 48(17): 108-144.
SUN Bing, BAO Dan, ZHANG Lei. Supplementary power control scheme for an MMC-HVDC station considering inertia and damping[J]. Power System Protection and Control, 2020, 48(17): 108-144.
[12] 张文嘉, 蔡晖, 王国腾, 等. 分散接入式混合直流系统的机电暂态建模与控制策略研究[J]. 高压电器, 2020, 56(9): 230-239.
ZHANG Wenjia, CAI Hui, WANG Guoteng, et al. Research on electromechanical transient modeling and control strategy of decentralized hybrid HVDC systems[J]. High Voltage Apparatus, 2020, 56(9): 230-239.
[13] 陈凌云, 程改红, 邵冲, 等. LCC-MMC型三端混合直流输电系统控制策略研究[J]. 高压电器, 2018, 54(7): 146-152.
CHEN Lingyun, CHENG Gaihong, SHAO Chong, et al. Research on control strategy for a 3-terminal LCC-MMC HVDC transmission system[J]. High Voltage Apparatus, 2018, 54(7): 146-152.
[14] 高泽盟, 李卫国, 杨洪达, 等. 应用于配网的MMC直流双极短路无闭锁故障穿越控制策略[J]. 高压电器, 2020, 56(6): 274-281.
GAO Zemeng, LI Weiguo, YANG Hongda, et al. Non-locking fault ride-through control strategy under DC bipolar short circuit of MMC for distribution network[J]. High Voltage Apparatus, 2020, 56(6): 274-281.
[15] COLE S, BEERTEN J, BELMANS R. Generalized dynamic VSC MTDC model for power system stability studies[J]. IEEE Transactions on Power Systems, 2010, 25(3): 1655-1662.
[16] CHAUDHURI N R, MAJUMDER R, CHAUDHURI B, et al. Stability analysis of VSC MTDC grids connected to multimachine AC systems[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2774-2784.
[17] BAYO-SALAS A, BEERTEN J, RIMEZ J, et al. Analysis of control interaction in multi-infeed VSC HVDC connections[J]. IET Generation, Transmission & Distribution, 2016, 10(6): 1336-1344.
[18] GUAN Rui, DENG Na, XUE Ying, et al. Small-signal stability analysis of the interactions between voltage source converters and DC current flow controllers[J]. IEEE Open Access Journal of Power and Energy, 2020, 7: 2-12.
[19] 郑征, 黄旭, 杨明, 等. 弱电网下逆变侧电流反馈的并网逆变器稳定性分析及优化[J]. 电力系统保护与控制, 2019, 47(19): 31-37.
ZHENG Zheng, HUANG Xu, YANG Ming, et al. Stability analysis and improvement for LCL filter grid-connected inverter using inverter-side current feedback[J]. Power System Protection and Control, 2019, 47(19): 31-37.
[20] SUN Jian. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[21] XU Ling, FAN Lingling. Impedance-based resonance analysis in a VSC-HVDC system[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2209-2216.
[22] XU Ling, FAN Lingling, MIAO Zhixin. DC impedance- model-based resonance analysis of a VSC-HVDC system[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1221-1230.
[23] PINARES G, BONGIORNO M. Analysis and mitigation of instabilities originated from DC-side resonances in VSC-HVDC systems[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2807-2815.
[24] PINARES G, BONGIORNO M. Modeling and analysis of VSC-based HVDC systems for DC network stability studies[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 848-856.
[25] JI Ke, TANG Guangfu, YANG Jie, et al. Harmonic stability analysis of MMC-based DC system using DC impedance model[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1152-1163.
[26] BEERTEN J, D’ARCO S, SUUL J A. Identification and small-signal analysis of interaction modes in VSC MTDC systems[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 888-897.
[27] AGBEMUKO A J, DOMINGUEZ-GARCIA J L, PRIRTO-ARAUJO E, et al. Dynamic modelling and interaction analysis of multi-terminal VSC-HVDC grids through an impedance-based approach[J]. International Journal of Electrical Power & Energy Systems, 2019, 113: 874-887.
[28] 王子豪, 牟龙华, 方重凯. 基于下垂控制的低压微电网故障控制策略[J]. 电力系统保护与控制, 2020, 48(22): 84-90.
WANG Zihao, MU Longhua, FANG Chongkai. Fault control strategy of a low-voltage microgrid based on droop control[J]. Power System Protection and Control, 2020, 48(22): 84-90.
[29] 章德, 田国梁, 谭玉东, 等. 提升交流系统暂态稳定性的多端直流最优紧急功率控制[J]. 电力系统保护与控制, 2020, 48(17): 37-44.
ZHANG De, TIAN Guoliang, TAN Yudong, et al. Optimal control of MTDC for improving rotor angle stability of AC systems[J]. Power System Protection and Control, 2020, 48(17): 37-44.
Mathematical model and analytical stabilizing condition of a droop-based single converter-infinite DC system
CHEN Jianxin1, ZHANG Xu2, MENG Haojie1, XU Yinfei1, REN Xinzhuo1, DENG Xiaodian1, LI Yujun2
(1. Hangzhou Electric Equipment Manufacturing Co., Ltd., Hangzhou 310018, China;2. School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
The droop-based converter plays an important role in a multi-terminal DC (MTDC) system because of its control flexibility. However, this imposes a great challenge on the stability of the DC grid. The main purpose of the paper is to examine the DC side stability of a single grid-connected VSC with the single input single output (SISO) method. The transfer function between the small perturbation of DC-link voltage and DC current at the end of transmission line is first constructed. Based on the SISO model, the stability criteria for a single VSC converter in different control modes is proposed by using the classical Routh judgement. A critical operation index, namely the DC power transfer limit, is defined to assess system stability. Finally, numerical simulation results validate the accuracy of the proposed stability analysis and the criteria for the droop-based converter.
droop-based converter; DC side stability; single input single output (SISO); Routh judgement; DC power transfer limit (DCPTL)
10.19783/j.cnki.pspc.210255
国家自然科学基金项目资助(51807150);杭州电力设备制造有限公司科技项目资助“交直流柔性互联配电网规划及协同控制技术研究与示范”(HD020112001039)
This work is supported by the National Natural Science Foundation of China (No. 51807150).
2021-03-10;
2021-05-23
陈建新(1971—),男,高级工程师,研究方向为智能用电技术及高低压设备技术;E-mail: hd_miller@163.com
张 旭(1999—),男,本科,研究方向为多端直流系统稳定性分析与控制;E-mail: yzsrzhangxu@163.com
孟浩杰(1993—),男,助理工程师,研究方向为电力系统运行与控制。E-mail: 15858170078@163.com
(编辑 姜新丽)

