基于CEEMDAN和改进时间卷积网络的短期风电功率预测模型

赵凌云，刘友波，沈晓东，刘代勇，吕 霜

基于CEEMDAN和改进时间卷积网络的短期风电功率预测模型

赵凌云1，刘友波1，沈晓东1，刘代勇2，吕 霜3

(1.四川大学电气工程学院，四川 成都 610065；2.国网四川省电力公司德阳供电公司，四川 德阳 618000；3.国网四川省电力公司成都供电公司，四川 成都 610000)

近年来，风力发电逐渐成为可再生能源发电的关键部分。为了提高风力发电功率短期预测的准确度，提出了一种将自适应噪声完备集成经验模态分解与改进时间卷积网络结合的短期风电功率预测模型。首先，利用CEEMDAN对风电功率序列进行分解，得到子序列分量，并分别与关键气象变量数据构成训练集。然后，使用基于时间模式注意力机制的时间卷积网络对子序列分量分别进行预测。最后，重构预测结果后得到最终的预测值。整个预测过程有助于精准刻画风电的分量特性，并通过TPA机制捕捉变量间的关联性，有效地提高风电功率的预测准确率。

风电功率预测；自适应噪声完备集成经验模态分解；时间卷积网络；时间模式注意力机制

0 引言

随着新能源的发展，风力发电逐渐成为最重要的绿色能源之一。目前，我国的风力发电并网比例增长十分迅速，具有良好的发展前景。风力发电的出力功率具有间歇性和不稳定性，会随着一些气象因素而发生较大的波动，如日间风速、风向以及大气压的变化等[1]。在提高风力发电系统并网运行的比例的同时，风力发电也会对电网的运行安全和稳定性造成比较大的影响[2-3]。因此，如何提高对风电的预测能力，在目前的风力发电发展进程中尤为重要[4]。

风电功率预测中使用较多的方法可以分为三类：物理方法、统计预测方法以及人工智能方法。其中，物理模型的建立过程较为复杂，其通过建立函数关系模型实现对风电功率的预测[5-6]。相比较于物理预测方法，统计预测方法建模过程更加简单[7-8]，其平均预测精度也高于传统的物理预测模型。人工智能方法通过对大量的风电功率历史记录数据对神经网络模型进行训练，再利用训练完毕的模型对时间序列的发展趋势进行预测。其中经典的方法有支持向量机[9-10]和人工神经网络[11-14]等。人工智能的预测方法相比于前两种方法能够更加有效地在时序建模中反应时间序列的变化趋势，但是单一的神经网络预测模型精度较低。

单一的预测方法预测误差较大，其最主要的原因在于风电功率曲线是一种典型的非平稳非线性的时间序列。针对风电功率的不平稳性，先对序列进行分解，再对子序列分别预测，最后进行重构的组合预测方法能有效地提高精度。其中，经验模态分解(Empirical Mode Decomposition, EMD)、变分模态分解(Variational Mode Decomposition, VMD)和小波变换(Wavelet Transform, WT)及其变式算法均为分解非线性时间序列的有效方法。文献[15-16]利用小波变换对原始序列分解，并通过支持向量机和人工神经网络进行预测，但组合预测模型中未分析关键变量对风电功率变化的影响。文献[17-18]使用了集合经验模态分解算法(Ensemble Empirical Mode Decomposition, EEMD)对序列进行分解预处理，预测模型分别采用了最小二乘支持向量机和小波神经网络。但EEMD分解算法仍存在子序列模态混叠与白噪声难以消除的问题。同时，分解子序列数量过多会导致误差叠加，增大组合模型的预测误差。文献[19]在变分模态分解后利用子模式的样本熵分析其复杂度，提出了一种自适应多层级综合预测模型。综合上述研究，分解-预测-重构的组合预测模型能够有效地提高风电功率预测的准确度。在此模型组合的基础上，若能选择重构误差更小的分解算法和预测精度更高的神经网络模型，则可以进一步提高组合模型的预测精度。

基于上述研究成果，本文提出了自适应噪声完备集成经验模态分解与基于时间模式注意力机制的时间卷积网络短期风电功率组合预测方法。首先，利用自适应噪声完备集成经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)算法对风电序列进行分解预处理，再使用时间模式注意力机制-改进时间卷积网络(Temporal Pattern Attention-Temporal Convolutional Network, TPA-TCN)神经网络对其子分量分别预测，最后重构分量的预测结果，得到最终的风电功率预测结果。算例结果表明，CEEMDAN分解能够更加有效地解决子序列模态混叠与白噪声难以消除的问题。而TPA-TCN模型能够捕捉各因素之间的非线性关联，有效地提高短期风电功率的预测精度。

1 风电功率时间序列的预处理

1.1 时间序列分解算法

经验模态分解(EMD)能够自适应地将时间序列分解为若干个独立的本征模态函数(Instrinsic Mode Function, IMF)分量以及一个残余分量。传统的EMD分解在非线性信号分解中应用最为广泛，但容易出现模态混叠的问题。集合经验模态分解(EEMD)对EMD做出了改进——对原始信号添加白噪声信号，分别进行多次EMD分解，将所得IMF分量进行平均计算，从而得到最终的IMF分量。其整个过程能够有效地克服EMD方法的模态混叠缺陷，但并未对添加的白噪声信号进行进一步消除，导致残留噪声较大，额外增加了分量的重构误差。

自适应噪声完备集成经验模态分解(CEEMDAN)针对EEMD分解做出了进一步改进—添加自适应白噪声，并在得到第一阶IMF后就进行总体平均计算，得到最终的IMF分量。其分解过程具有完整性，相比EEMD算法，分量重构误差大大降低[20]。作为EEMD和EMD的改进算法，CEEMDAN能够同时具有较小的模态混叠现象和较小的分量重构误差。其具体的分解流程如下所述。

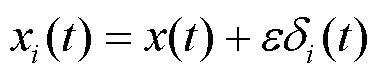
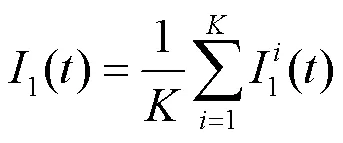
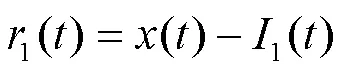
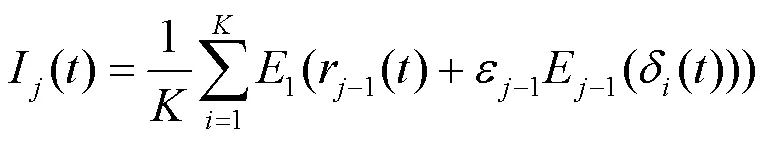
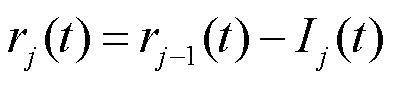
4) 重复上述步骤，直到残余分量极值点个数减小到一定数量(通常设定小于等于2)，不能够继续分解，则CEEMDAN分解结束。此时原始信号被分解为若干个IMF分量与一个残余分量。

本文对上述迭代停止准则进行改进，人为设定生成的IMF个数作为CEEMDAN算法的迭代停止条件[21]。通过调整分解生成的IMF个数，能够进一步降低模态混叠现象。

1.2 排列熵

针对每个分解得到的子序列分量，可以通过排列熵(Permutation Entropy, PE)的大小衡量时间序列的复杂度[22]。排列熵越大，说明时间序列越复杂，反之，说明时间序列越规律。对于不同的分解算法，若分解得到的各个子分量排列熵差异越小，则证明其分解结果的模态混叠现象越严重，反之，则证明其结果模态混叠现象越少。排列熵原理如下所述。

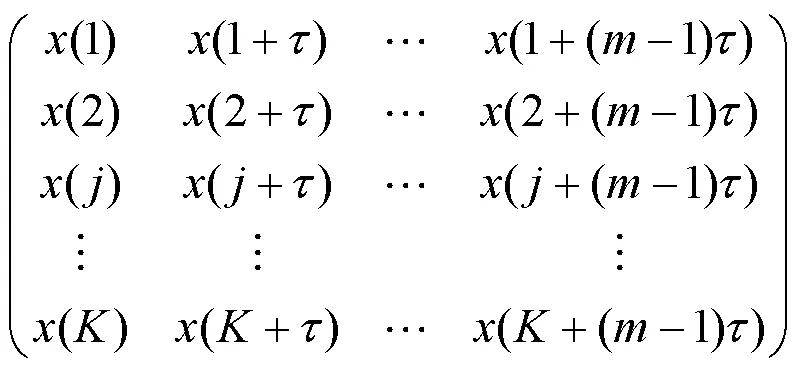
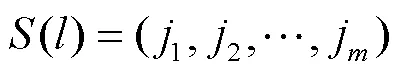
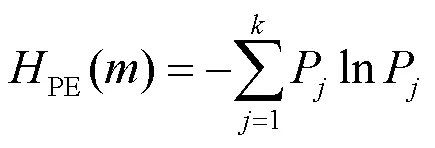
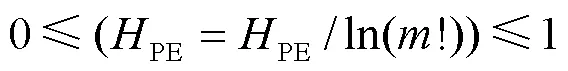
2 TPA-TCN预测模型

2.1 风力发电特性分析

风能具有可再生、无污染和成本低的优点，是一种有较大开发价值的新能源。拥有风能资源的各个地区所处的纬度不同，海拔也不同，导致气候类型有较大的差异，这对于风的特性具有重要的影响[23]。各个因素导致了自然风不可控，并且使得风电的输出功率具有较大的随机性和波动性。显然，一些关键的气象因素能够直接影响风电功率的大小，例如，风速是影响风电功率大小最直接的因素之一，风电输出功率与风速之间具有明显的正相关性质。

除此之外，根据风电场的位置与朝向，风向也会对发电功率产生影响。同时气温、大气压和湿度等因素的影响也会使风电功率发生变化，但是各个因素对风力变化的影响方式各不同，程度也有差异[24]。因此，对气象数据与风电功率的关联性的特征捕捉是提高风电功率预测准确度的关键。

2.2 时间卷积网络

时间卷积网络[25]是针对时间序列预测的有效模型，其针对一维卷积网络的预测模型做出了改造。TCN的核心组件是因果扩张网络，其结构如图1所示，其优点并不是与传统卷积网络一样经过池化过程，而是直接通过一系列的扩张卷积逐渐增加感受野，使输出拥有丰富的信息。在因果扩张卷积中，可以通过调整卷积核、卷积层数和扩张系数等参数实现对长时间序列整体特征的捕捉，使得序列对深层网络的影响进一步加深。

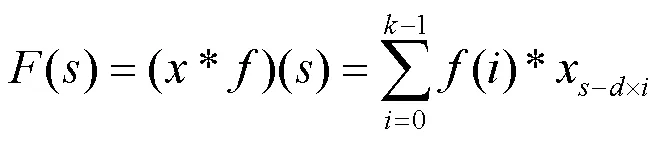
图1 因果扩张卷积

Fig. 1 Causal expansion convolution

因果扩张网络中，弧线连接的部分是残差模块，其可以解决TCN层数变深后可能出现的信息丢失问题。该模块的原理是在进行卷积操作之后，将输入叠加到输出上，从而使得信息不被丢失。将两个因果扩张卷积层加上与之配套的各种模块组成一个残差模块作为TCN网络的基本单元，其结构如图2所示。

HIV基因组全长约9.7 kb，含有gag、pol和env 3个结构基因、2个调节基因（tat反式激活因子和rev毒粒蛋白表达调节因子）和4个辅助基因 （nef负调控因子、vpr病毒蛋白r、vpu病毒蛋白u和vif病毒感染因子）。

图2 TCN残差模块

Fig. 2 TCN residual module

2.3 基于时间模式注意力的时间卷积网络模型

如上文所述，在风电功率的实际预测中，重要的数据不仅包括历史风电的功率数据，更包括风速、风向、温度等多元变量。多元变量与时间序列组成多元时间序列后，基于时间模式的注意力机制(TPA)[26]能够在预测模型中捕捉各变量对预测序列的影响，有效提高了预测精度。为了解决变量之间存在的复杂、动态并且相互依赖的关系，本文对时间卷积网络做出改进，并提出了TPA-TCN模型。在图3的TPA-TCN网络结构中，第一层使用TCN提取时间序列的特征，第二层使用TPA机制捕捉变量之间的依赖性，最终输出预测结果。其中彩色方框代表时间模式注意层的行卷积过程。

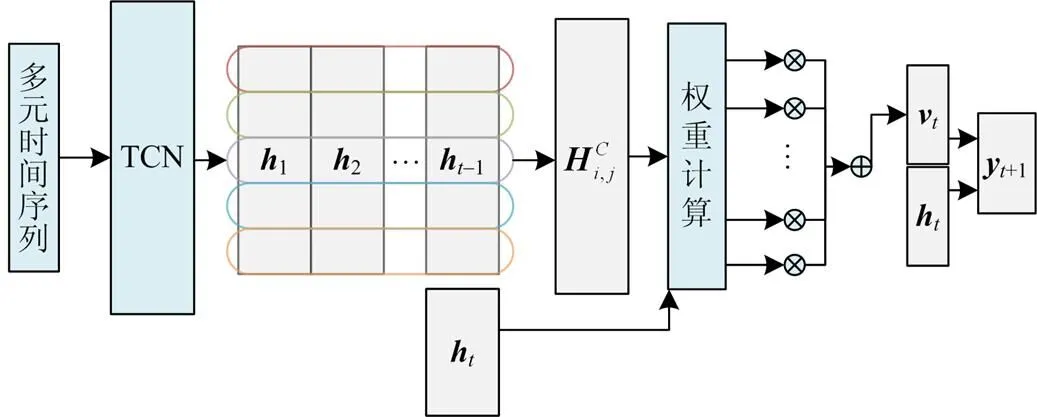
图3 TPA-TCN预测模型

1) TCN层

第一层是TCN时间卷积网络层，给定输入多维时间序列，使用TCN捕捉时序信息。TCN层的输出是每个时间步的隐藏状态，输出在时刻的隐藏信息，可由式(12)表示。

2) 时间模式捕捉层

单层CNN善于提取各种重要信号的特征，第二层使用CNN作为时间模式捕捉层。

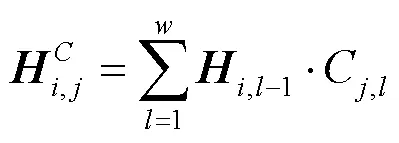
3) 时间模式注意层

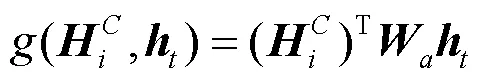
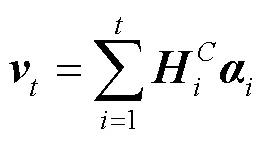
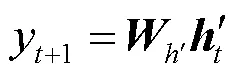
3 建模与数据预处理

3.1预测模型流程

综合上文的建模过程，可以得到CEEMDAN- TPA-TCN组合预测模型的预测流程，如图4所示。组合模型的具体预测步骤如下：

2) 将原始数据分解后的各个分量与关键变量数据组成训练集输入TPA-TCN模型，得到各个分量预测后的结果。

3) 将各个分量的预测值结果进行叠加重构，得到最终的风电功率预测值。

4) 将得到的风电功率预测值与实际的风电功率数据对比，分析误差。

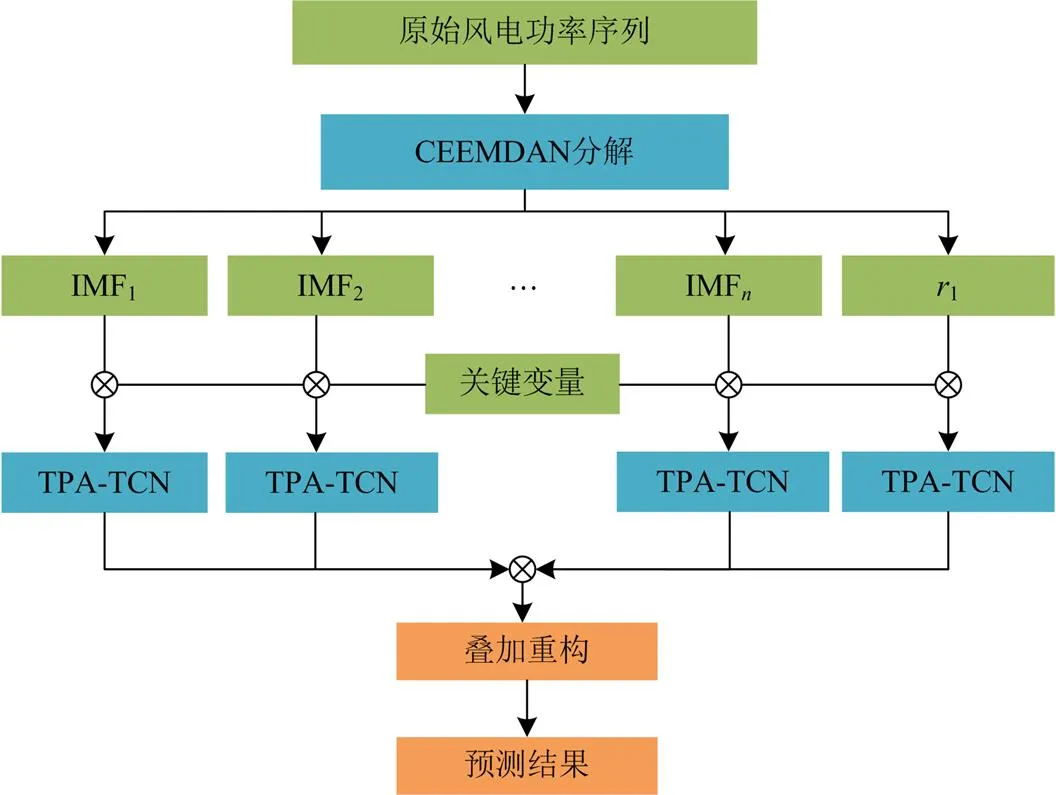
图4 风电功率预测流程图

3.2 数据预处理

3.2.1归一化

对于风电功率、风向、风速等采集的数据，数量单位和数量级都不同，同时神经元的输出范围在0和1之间。为了避免神经元过饱和，将所有样本的历史数据做归一化处理使其为[0,1]的数据。

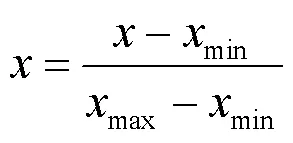
3.2.2预测误差评价指标选取

为了保证能够对整体模型的准确率进行有效评价，本文选择了两种用于评判时序序列预测模型的评价指标，分别为平均相对误差(Mean Absolute Percentage Error, MAPE)和均方根误差(Root Mean Squard Error, RMSE)，计算公式为

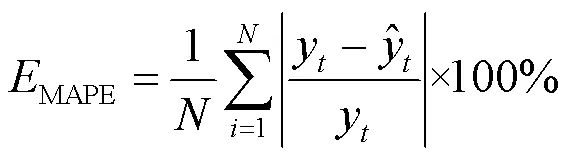
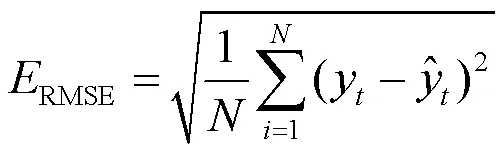
3.2.3风电功率序列预处理

原始风电功率序列具有较大的随机性和波动性，需要通过分解算法对其进行预处理。本节实验选用EEMD作为CEEMDAN的对比算法，比较二者的重构误差以及模态混叠现象。在EEMD与CEEMDAN分解中，一般取0.01～0.5倍标准差和150～300次范围内的白噪声得到的分解效果最好[27]。实验将EEMD与CEEMDAN加入的白噪声标准差设置为0.25，总集合次数设置为100次。

将CEEMDAN分解生成的IMF个数在3～9个内进行调整，不断计算在不同迭代停止条件下的分量重构误差。实验结果表明，IMF个数设置为4时，CEEMDAN能将重构误差降到最低。

将残余分量极值点小于等于1作为迭代停止条件，对原始的风电功率时间序列进行EEMD分解，逐步分离出了11个IMF分量和1个残余分量。两组分解结果如图5和图6所示，图中采样点为5 000个，采样间隔为15 min，图中第一个序列均为原始风电功率。

针对同一组风电功率序列，取子序列进行重构，并与实际的原始序列进行比较，计算两种算法的重构误差，结果如表1所示。

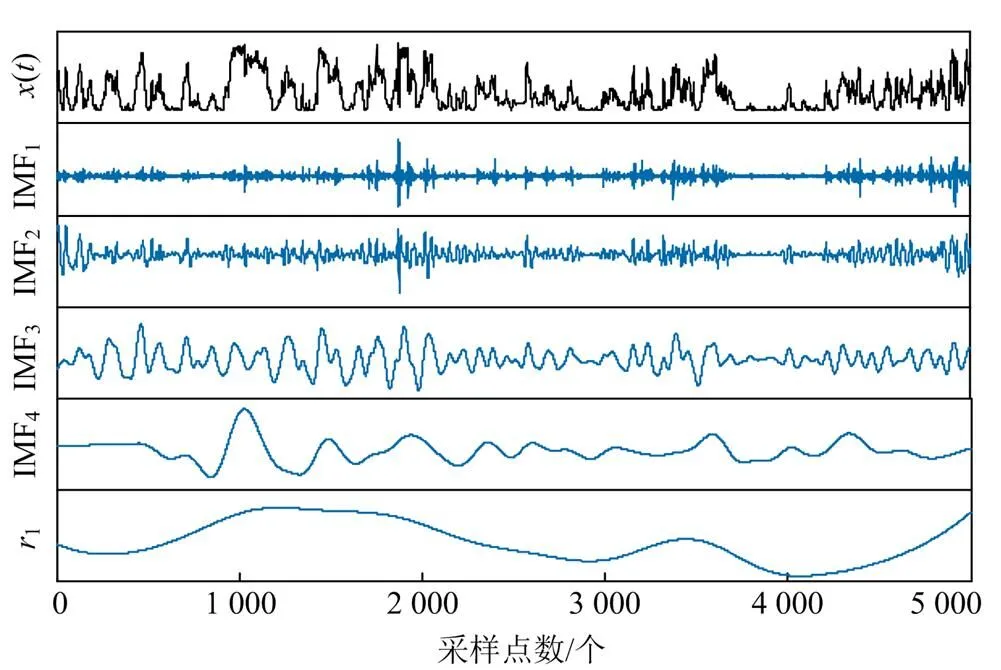
图5 风电功率序列的CEEMDAN分解结果

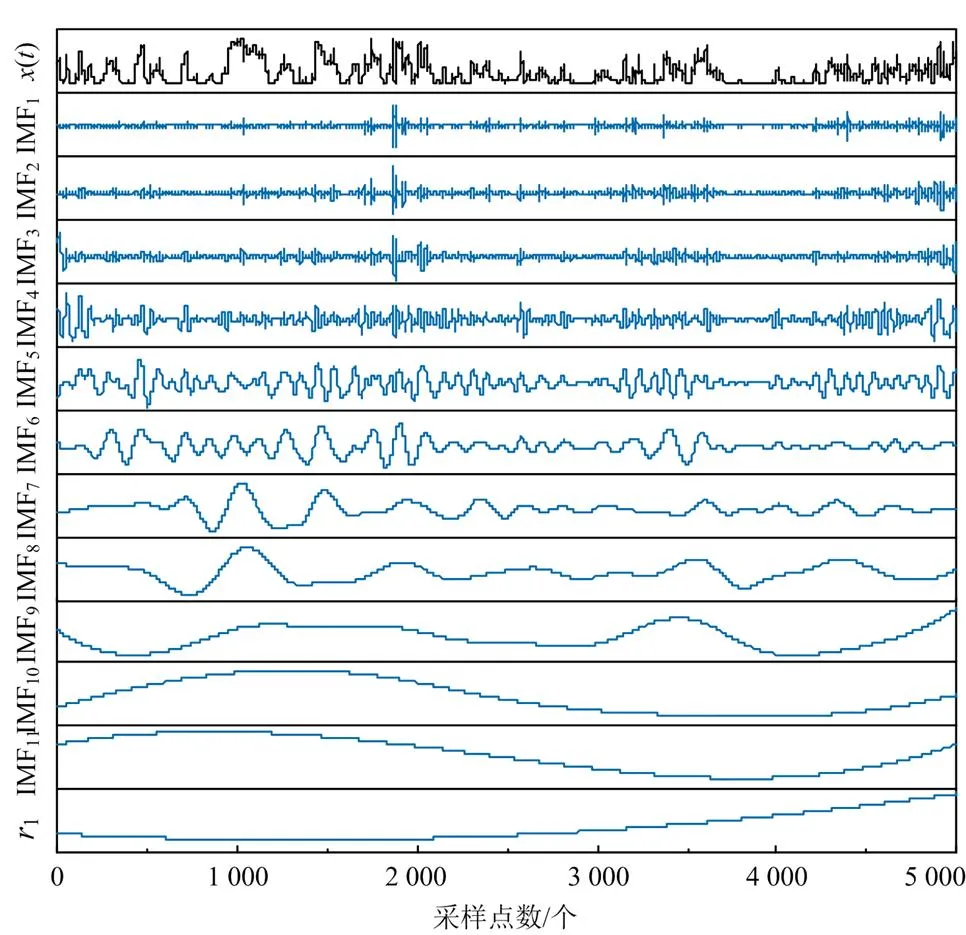
图6 风电功率序列的EEMD分解结果

表1 重构误差

实验结果表明，CEEMDAN子序列重构误差远远小于EEMD子序列，证明了CEEMDAN算法能够有效地消除残余白噪声影响。

从图5、图6中可得，两种分解方式产生的子序列复杂度均逐渐减小。其中EEMD各个子序列复杂度相近，而CEEMDAN子序列数目更少，相邻子序列之间的复杂度差异相比EEMD更大。

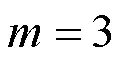
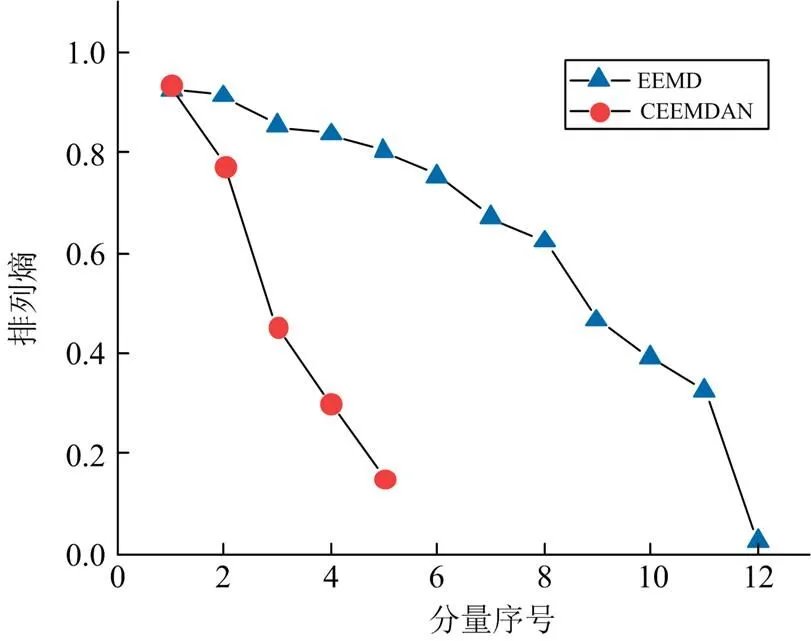
图7 两种分解算法子序列的排列熵

由图7可知，各个子序列的排列熵值随着其频率的降低而降低，即分解得到的子序列非平稳性逐渐减低，趋势越来越规律。但EEMD分解子序列IMF1～IMF8和IMF9～IMF11排列熵值接近，说明其子序列仍然存在一定的模态混叠现象。而经过对停止迭代条件的改进，CEEMDAN分解子序列数量更少，并且排列熵值变化跨度更大，子序列不存在明显的模态混叠现象。

4 算例测试

本文算例的数据集为宁夏某风电场2013年2月—2013年4月所采集的实际风电功率数据，并包括传感器中收集的风速、风向、温度、湿度和大气压五个类型的主要气象数据。

其中，算例中样本个数均为5 000个，每两个样本点之间的时间间隔为15 min。所有的预测实验中均选取最后192个采样点(两日)作为测试集，其余为训练集。为了对比验证模型的精度，实验一采用了TPA-TCN和EEMD-TPA-TCN作为CEEMDAN- TPA-TCN的对比算法进行实验，以分析CEEMDAN预处理对组合预测模型精度的影响。实验二采用CEEMDAN-TCN、CEEMDAN-LSTM和CEEMDAN- BP作为CEEMDAN-TPA-TCN的对比算法进行实验，以分析TPA-TCN模型预测效果。

4.1预测模型超参数

在对原始序列分解并进行归一化处理后，对于不同的重构分量，根据其不同的特征对数据批大小b_size、学习速率lr、随机失活比率Dropout和残差块扩张系数等超参数设置进行反复实验，得到最优的CEEMDAN-TPA-TCN超参数组合，见表2。

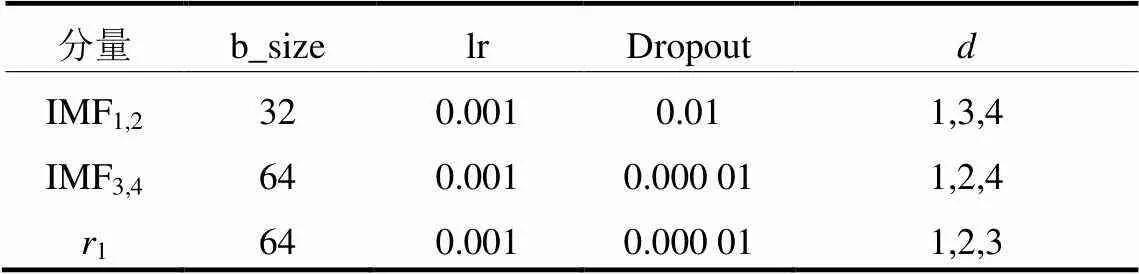
表2 训练参数设置2

在反复实验中发现，更高的扩张系数能够对高频重构分量有更好的预测效果。与上文分析的结果相同，更高的扩张系数能够获得更大的卷积感受野，从而更加精准地捕捉高频分量的整体序列特征，忽略局部的变化趋势，即较大的扩张系数更适用于高频率分量的预测。

其余训练超参数(如卷积核大小k_size、优化器Optimizer、激活函数Activation和训练epoch)的设置如表3所示。TPA-TCN模型搭建采用Python语言编写，在Keras深度学习框架下实现。

表3 训练参数设置1

4.2 结果分析

4.2.1 CEEMDAN单步预测结果分析

本节对分解算法的性能进行了研究。设定合适的超参数后，将数据集输入预测模型中，可以得到子分量序列的预测值。其中，采用TPA-TCN(F)和EEMD-TPA-TCN(E)作为CEEMDAN-TPA-TCN(A)的对比算法进行实验，并且不同模型均采用单步预测的预测形式。在对比实验中，不同预测模型的预测误差如表4所示，单步预测的结果如图8所示。

表4 单步预测误差1

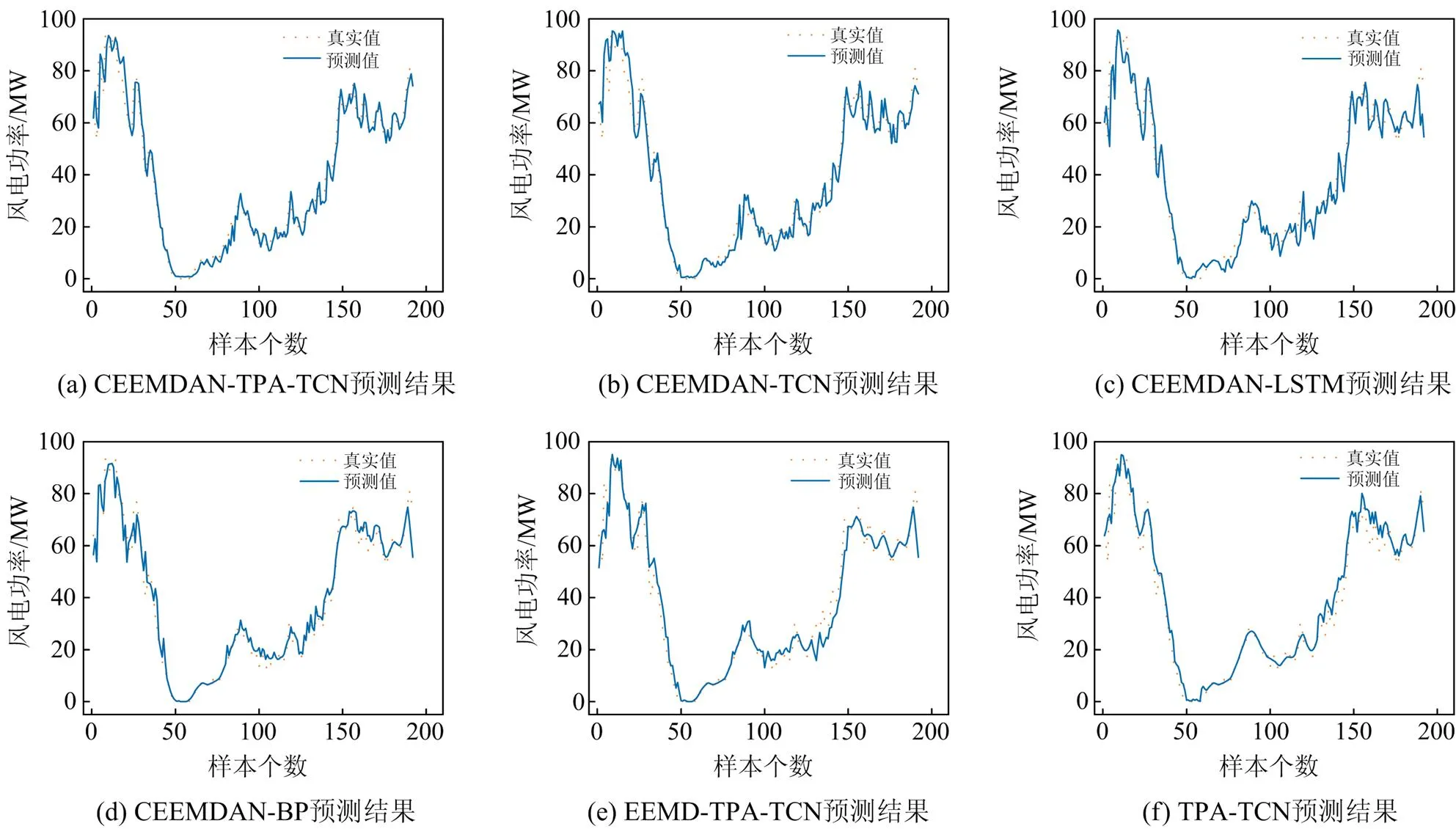
图8 单步预测结果

相较于未进行分解预处理的TPA-TCN单一预测模型，其经过EEMD和CEEMDAN分解预处理的对应预测模型精度都有一定幅度的提高，单步预测在单一模型基础上分别降低了15.7%和67.4%。算例表明序列分解的预处理对提高预测精度有着重要的意义，而CEEMDAN对组合预测模型精度提升更大，CEEMDAN是一种优于EEMD的分解算法，与上文的理论分析相符。

4.2.2 TPA-TCN单步预测结果分析

本节对TPA-TCN预测模型性能进行了分析。采用CEEMDAN-TCN(B)、CEEMDAN-LSTM(C)和 CEEMDAN-BP(D)作为CEEMDAN-TPA-TCN(A)的对比算法进行实验，预测均采用单步预测的形式。在对比实验中，不同预测模型的预测误差如表5所示，单步预测的结果如图8所示。

表5 单步预测误差2

在同样进行了CEEMDAN预处理的四种组合预测方法中，CEEMDAN-TPA-TCN预测精度最高。证明TPA-TCN模型能够通过有效地捕捉变量关联信息，进一步提高组合模型的预测精度。

4.2.3 多步预测分析

为了进一步验证提出的CEEMDAN-TPA-TCN组合预测方法的精度，本节对风电功率序列进行了多步预测，预测误差结果如表6所示。本文采用的多步预测方式为滚动预测，即利用单步预测结果替换历史监测数据来构建单步预测模型的输入序列，并实现多步的滚动预测。由于多步预测会造成误差的累积效应，六种预测模型的预测误差都随着预测步数的增加而增加，多步预测精度均随着预测步数的上升而有下降。从表中可得，CEEMDAN- TPA-TCN组合模型多步预测的误差指标依然优于其他的对比模型，仍拥有最佳的预测性能。

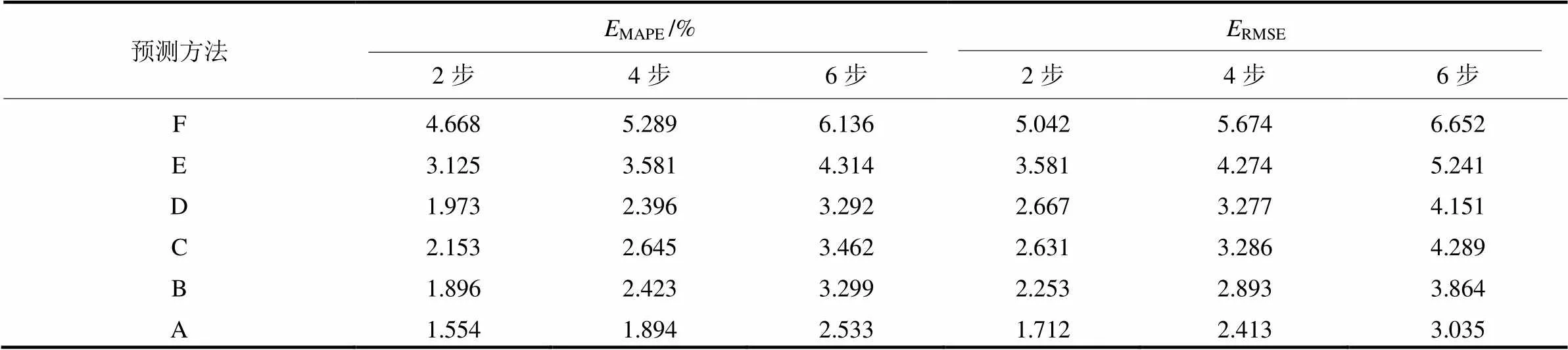
表6 多步预测误差

5  结论

本文提出了一种将自适应噪声完备集成经验模态分解和基于时间模式注意力机制的时间卷积网络结合的风电功率短期预测组合模型，经过计算案例的分析表明：CEEMDAN算法能够有效地克服EEMD算法残余白噪声大的缺点，并有效地削弱子分量模态混叠的现象。同时，TPA-TCN预测模型能够捕捉关键变量与风电功率之间的非线性联系，提高组合模型的预测精度。

本文所提出的CEEMDAN-TPA-TCN模型能够更加准确地识别风电功率变化趋势，在实际生产中能够为发电厂提供更准确的风电功率预测数据，是一种具有更好预测表现的组合预测模型。

[1] SONG Dongran, YANG Jian, FAN Xinyu, et al. Maximum power extraction for wind turbines through a novel yaw control solution using predicted wind directions[J]. Energy Conversion and Management, 2018, 157.

[2] 施涛, 李春来, 朱慧敏. 考虑功率预测不确定性的风电消纳随机调度[J]. 电网与清洁能源, 2019, 35(4): 55-59.

SHI Tao, LI Chunlai, ZHU Huimin. Stochastic dispatching of wind power accommodation considering uncertainty of power prediction[J]. Power System and Clean Energy, 2019, 35(4): 55-59.

[3] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.

LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.

[4] ZHENG D, ESEYE A T, ZHANG J, et al. Short-term wind power forecasting using a double-stage hierarchical

ANFIS approach for energy management in microgrids[J]. Protection and Control of Modern Power Systems, 2017, 2(2): 136-145.

[5] 郑紫宸, 符杨, 时帅, 等. 考虑气象相似性与数值天气预报修正的海上风功率预测[J]. 电网技术, 2019, 43(4): 1253-1260.

ZHENG Zichen, FU Yang, SHI Shuai, et al. Offshore wind power forecasting considering meteorological similarity and NWP correction[J]. Power System Technology, 2019, 43(4): 1253-1260.

[6] WANG Jianzhou, SONG Yiliao, LIU Feng, et al. Analysis and application of forecasting models in wind power integration: a review of multi-step-ahead wind speed forecasting models[J]. Renewable and Sustainable Energy Reviews, 2016, 60.

[7] ERDEM E, SHI J. ARMA based approaches for forecasting the tuple of wind speed and direction[J]. Applied Energy, 2010, 88(4).

[8] AMBACH D, SCHMID W. A new high-dimensional time series approach for wind speed, wind direction and air pressure forecasting[J]. Energy, 2017, 135.

[9] 杨洪, 古世甫, 崔明东, 等. 基于遗传优化的最小二乘支持向量机风电场风速短期预测[J]. 电力系统保护与控制, 2011, 39(11): 44-48, 61.

YANG Hong, GU Shifu, CUI Mingdong, et al. Forecast of short-term wind speed in wind farms based on GA optimized LS-SVM[J]. Power System Protection and Control, 2011, 39(11): 44-48, 61.

[10] 田壁源, 刘琪, 张新燕, 等. 基于APSO-GSA和相关向量机的短期风电功率预测[J]. 电力系统保护与控制, 2020, 48(2): 107-114.

TIAN Biyuan, LIU Qi, ZHANG Xinyan, et al. Short-term wind power prediction based on APSO-GSA and correlation vector machine[J]. Power System Protection and Control, 2020, 48(2): 107-114.

[11] 崔嘉, 杨俊友, 杨理践, 等. 基于改进CFD与小波混合神经网络组合的风电场功率预测方法[J]. 电网技术, 2017, 41(1): 79-85.

CUI Jia, YANG Junyou, YANG Lijian, et al. New method of combined wind power forecasting based on improved CFD and wavelet-HNN model[J]. Power System Technology, 2017,41(1): 79-85.

[12] 朱乔木, 李弘毅, 王子琪, 等. 基于长短期记忆网络的风电场发电功率超短期预测[J]. 电网技术, 2017, 41(12): 3797-3802.

ZHU Qiaomu, LI Hongyi, WANG Ziqi, et al. Short-term wind power forecasting based on LSTM[J]. Power System Technology, 2017, 41(12): 3797-3802.

[13] 汪欣, 蔡旭, 李征. 结合交叉局部异常因子和注意力机制的超短期风电功率预测方法[J]. 电力系统保护与控制, 2020, 48(23): 92-99.

WANG Xin, CAI Xu, LI Zheng. Ultra-short-term wind power forecasting method based on a cross LOF preprocessing algorithm and attention mechanism[J]. Power System Protection and Control, 2020, 48(23): 92-99.

[14] 周松林, 茆美琴, 苏建徽. 基于主成分分析与人工神经网络的风电功率预测[J]. 电网技术, 2011, 35(9): 128-132.

ZHOU Songlin, MAO Meiqin, SU Jianhui. Prediction of wind power based on principal component analysis and artificial neural network[J]. Power System Technology, 2011, 35(9): 128-132.

[15] LIU Da, NIU Dongxiao, WANG Hui, et al. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm[J]. Renewable Energy, 2014, 62.

[16] LIU Hui, TIAN Hongqi, CHEN Chao, et al. An experimental investigation of two wavelet-MLP hybrid frameworks for wind speed prediction using GA and PSO optimization[J]. International Journal of Electrical Power and Energy Systems, 2013, 52.

[17] LIANG Zhengtang, LIANG Jun, ZHANG Li, et al. Analysis of multi-scale chaotic characteristics of wind power based on Hilbert-Huang transform and Hurst analysis[J]. Applied Energy, 2015, 159.

[18] 王贺, 胡志坚, 陈珍, 等. 基于集合经验模态分解和小波神经网络的短期风功率组合预测[J]. 电工技术学报, 2013, 28(9): 137-144.

WANG He, HU Zhijian, CHEN Zhen, et al. A hybrid model for wind power forecasting based on ensemble empirical mode decomposition and wavelet neural networks[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 137-144.

[19] 张亚超, 刘开培, 秦亮. 基于VMD-SE和机器学习算法的短期风电功率多层级综合预测模型[J]. 电网技术, 2016, 40(5): 1334-1340.

ZHANG Yachao, LIU Kaipei, QIN Liang. Short-term wind power multi-leveled combined forecasting model based on variational mode decomposition-sample entropy and machine learning algorithm[J]. Power System Technology, 2016, 40(5): 1334-1340.

[20] GAO B, HUANG X, SHI J, et al. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks[J]. Renewable Energy, 2020, 162.

[21] 郑红梅, 彭丹丹, 顾森茂, 等. 基于CMSE的随钻脉冲信号提取算法研究[J]. 电子测量与仪器学报, 2018, 32(3): 170-176.

ZHENG Hongmei, PENG Dandan, GU Senmao, et al. Research on drill pulse signal extraction algorithm based on CMSE[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(3): 170-176.

[22] CHRISTOPH B, BERND P. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17).

[23] CHITSAZ H, AMJADY N, ZAREIPOUR H. Wind power forecast using wavelet neural network trained by improved clonal selection algorithm[J]. Energy Conversion and Management, 2015, 89.

[24] LAHOUAR A, SLAMA J B H. Hour-ahead wind power forecast based on random forests[J]. Renewable Energy, 2017, 109.

[25] BAI S, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. [2018-04-19]. https://arxiv. org/pdf/1803.0127.

[26] SHIH S, SUN F, LEE H. Temporal pattern attention for multivariate time series forecasting[J]. Machine Learning, 2019, 108(8-9).

[27] 程启明, 陈路, 程尹曼, 等. 基于EEMD和LS-SVM模型的风电功率短期预测方法[J]. 电力自动化设备, 2018, 38(5): 27-35.

CHENG Qiming, CHEN Lu, CHENG Yinman, et al. Short-term wind power forecasting method based on EEMD and LS-SVM model[J]. Electric Power Automation Equipment, 2018, 38(5): 27-35.

Short-term wind power prediction model based on CEEMDAN and an improved time convolutional network

ZHAO Lingyun1, LIU Youbo1, SHEN Xiaodong1, LIU Daiyong2, LÜ Shuang3

(1. College of Electrical Engineering, Sichuan University, Chengdu 610065, China;2. Deyang Power Supply Company, State Grid Chengdu Electric Power Company, Deyang 618000, China;3. Chengdu Power Supply Company, State Grid Chengdu Electric Power Company, Chengdu 610000, China)

In recent years, wind power has gradually become a key part of renewable energy generation. In this paper, an effective short-term wind power forecasting combination model is proposed by combining complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and an improved temporal convolutional network (TCN) to improve the accuracy of short-term wind power prediction. First, CEEMDAN is used to decompose the wind power series to obtain the subsequence components, and the subsequence components are combined with the data of key meteorological variables to form the training set. Then, the time convolution network based on temporal pattern attention (TPA) is used to predict the subsequence components, and the final prediction value is obtained after reconstructing the prediction results. The whole prediction process helps to accurately describe the component characteristics of wind power, and capture the correlation between variables through the TPA mechanism, and this effectively improves the prediction accuracy of wind power.

wind power prediction; complete total empirical mode decomposition based on adaptive white noise; time convolution network; time mode attention mechanism

10.19783/j.cnki.pspc.210252

国家自然科学基金项目资助(51977133)；国家自然科学基金重点项目资助(U2066209)

This work is supported by the National Natural Science Foundation of China (No. 51977133).

2021-03-09；

2021-05-11

赵凌云(1998—)，男，硕士研究生，研究方向为电力系统人工智能技术；E-mail: 913964776@qq.com

刘友波(1983—)，男，博士，副教授，主要研究方向为主动配电网规划与运行、电力系统的机器学习算法等；E-mail: liuyoubo@scu.edu.cn

，博士，副教授，研究方向为园区多能源系统优化等。E-mail: shenxd@sch.edu.cn

(编辑 姜新丽)