基于单环寻优策略的有源配网重构方法

于艾清，丁丽青，王育飞，李 豪

基于单环寻优策略的有源配网重构方法

于艾清，丁丽青，王育飞，李 豪

(上海电力大学电气工程学院，上海 200090)

配网DG接入导致智能优化算法在重构求解时易陷入局部收敛且寻优率较低。考虑配网拓扑特性与算法的关系，将两者深度结合，提出基于单环寻优策略的有源配网重构方法。首先引入莱维飞行对量子粒子群算法进行改进，建立了莱维系数量子粒子群算法。其次提出自适应环压有序环矩阵作为算法的解空间。最后根据配网拓扑与算法全局最优解之间的对应关系提出单环寻优策略，与算法深度结合进行求解。通过改进算法、优化解空间、配网拓扑与算法深度结合三个角度提高算法全局搜索能力和寻优效率。通过对多个电力系统进行仿真分析，验证所提算法和策略的有效性和适用性。

有源配网重构；改进算法；配网结构；优化解空间；单环寻优策略

0 引言

配网重构可使配电网在最优拓扑结构下运行，实现降低网损、提高配网运行经济性、提高供电稳定性和可靠性等目标[1]。而多样化的分布式电源(Distributed Generation, DG)接入配网后改变了配网运行的电气特性[2-4]，提高了配网运行复杂度和重构求解难度，优化拓扑可提高DG消纳[5]。

有源配网重构的主要研究方向为优化求解方法和优化求解对象两个角度。求解方法主要有数学规划[6-8]、启发式方法[9]和智能算法[10-14]。数学规划主要是基于配网运行约束条件，将重构问题转化为凸规划问题，降低DG不确定性对配网的影响[6]，实现配网协调、经济运行[7]，在求解速度和准确性上具有一定优势。启发式方法是基于对配网中电压和潮流的数学分析得到的求解方法[9]，潮流计算次数较少，求解速度较快，但其着重配网局部特性，依赖配电网拓扑结构，当DG接入导致结构复杂时较难得到最优解。应用较为广泛的是智能算法，如离散学习优化算法[10]、粒子群算法(Particle Swarm Optimization, PSO)、改进萤火虫算法[11]、细菌觅食优化算法[12]和教与学优化算法[13]等，由于是在解空间内全局、随机、盲目性搜索，无法保证全局最优，易出现早熟问题。因此有学者研究混合算法，如多个智能算法的混合以及启发式方法和智能算法的结合[14]，并取得研究成果。算法的求解空间是基于配网拓扑生成，即求解对象是配网，解的质量将直接影响算法的寻优效率，因此优化解空间是提高算法寻优率和收敛速度的方式之一，优化结果优于对算法自身的改进。文献[15-18]通过划分、压缩、分块重组及分环替代等方式缩小解空间规模，使算法在可行解范围内进行搜索，提高寻优率，但其仅从解空间分析，并未考虑DG对配网的影响，因此算法仍易陷入局部收敛。

以上文献研究结果说明算法性能和解空间特性均影响重构计算结果的优劣，但均未考虑有源配网结构特性与算法之间的关系。由于算法得到的全局最优解与配网结构之间具有对应关系，此时可利用拓扑结构的特性对算法寻优过程进行指导。基于此，本文首先对量子粒子群算法(Quantum Particle Swarm Optimization, QPSO)进行改进，建立了莱维系数量子粒子群算法(Levy Coefficient Quantum Particle Swarm Optimization, LCQPSO)，使粒子增加了莱维突跳特性；其次提出自适应环压有序环矩阵作为算法的解空间；最后根据配网拓扑与算法全局最优解之间的对应关系提出单环寻优策略(Single Loop Optimization, SLO)，与算法动态融合实现局部搜索与全局寻优相互配合。通过改进算法、优化解空间、配网拓扑与算法深度结合三个角度共同提高算法全局搜索能力和寻优效率。

1 配电网重构模型

以系统网损最小为目标函数，为

电网运行约束条件包括潮流约束、配网辐射结构约束、节点电压约束和支路容量约束，如式(2)—式(5)。

1) 功率平衡约束

2) 配网辐射约束

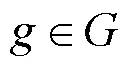
式中：为当前配电网运行结构；为配电网所有辐射状结构的集合。

3) 节点电压约束

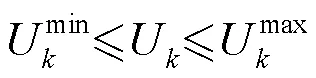
4) 支路容量约束

2 莱维系数量子粒子群算法

QPSO算法是对粒子群算法进行改进，提高了全局搜索能力和粒子协同搜索能力[19]。公式为

QPSO算法的全局搜索能力较强，在寻优中后期算法收敛速度较慢且易陷入局部收敛，因此引入莱维飞行对QPSO算法进行改进以提高收敛速度并改善早熟现象。莱维飞行是一种符合莱维分布的随机步长。步长计算公式为

参数的方差公式为

图1 突跳能力对比

Fig. 1 Comparison of jumping ability

由图1看出，莱维系数的突跳幅值明显高于QPSO突跳系数，对促进算法跳出局部收敛更有效，因此用莱维系数替代QPSO突跳系数，可得到具有莱维系数的QPSO算法，为

步长控制系数采用式(10)进行更新。

3 自适应环压有序环矩阵与环路编码

提出自适应环压有序环矩阵作为算法的解空间，基于环路对开关进行编码。

3.1自适应环压有序环矩阵

3.1.1基本环

在辐射电网中，闭合一条联络开关，网络中出现一条环网，由环内一条联络开关和所有分段开关组成的回路称为基本环，基本环的数量与环网数相等。以图2所示的IEEE33节点系统为例，开关编号为括号内序号，配网中含有5个联络开关，因此可形成5个环网，如图2中所示5个基本环。

图2 IEEE33节点配网

3.1.2基本环矩阵

由所有基本环构成的矩阵定义为基本环矩阵0，因此0中每一行均表示一个基本环，行数为环网数。由图2得到的0[20]为式(11)。

3.1.3有序环矩阵

由0看出，每个基本环内非零开关一般是按编号从小到大排列，并未考虑配网结构的特点，此矩阵作为算法的解空间会使算法搜索效率低且易早熟。文献[14]建立有序环矩阵，方法为：在每个基本环内，将功率流入节点相邻的一条支路放在基本环的第一位，另一边相邻的支路放在末位，不计0元素，其余开关根据连接关系依次排序，将排序后的基本环定义为有序基本环，由所有有序基本环构成有序环矩阵，为式(12)。

有序环矩阵可提高算法寻优效率，但也存在早熟现象，这是由于虽然考虑了配网结构的特点，但并未考虑配网结构与算法间的关系。

3.1.4自适应环压有序环矩阵的建立

图2中环1和环3之间存在公共开关2至开关7和开关18至开关20，环2和环4之间存在公共开关9至开关14，因此通过删除环3和环4中的公共开关简化有序环矩阵。其次，单环内使网损最小时断开的支路一般在环内最低电压节点附近[9]。基于此，本文依据环网内节点电压对简化后的有序环矩阵中每个有序基本环内的开关进行重新排序。首先闭合所有联络开关，通过潮流计算得到各个环网内最高电压节点为{2,9,21,6,3}，将最高电压节点两边邻接的开关其中一个放在有序基本环的第一位，另一边相邻的开关放在末位，不计0元素，其余开关根据连接关系依次排序，将排序后的有序基本环定义为环压有序基本环，由所有环压有序基本环构成环压有序环矩阵V，为

当负荷变化或DG使最高电压节点发生变化，V随之变化，因此V为自适应环压有序环矩阵。

3.2 环路编码

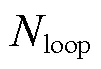
表1 环内支路编码信息

4 单环寻优策略

基于配网拓扑与算法间的关系提出单环寻优策略，并与算法深度结合。

4.1 配网拓扑与算法间的关系

4.2 递进有序环矩阵

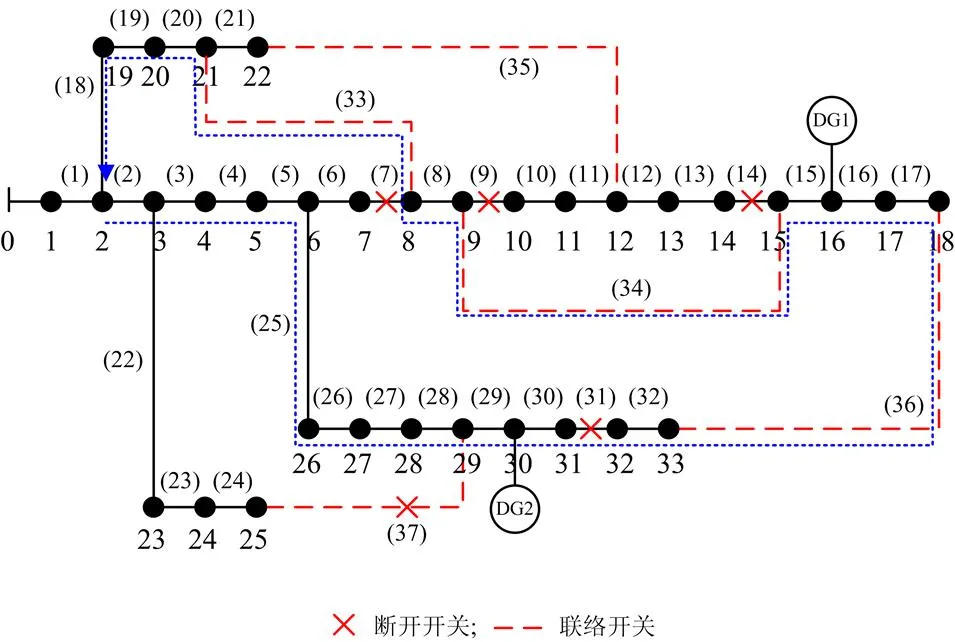
图3 IEEE33配网某一拓扑结构

4.3 含DG的单环网特性

文献[9]从电压降和潮流计算的角度得出结论：断开环路中电压最低点两侧的某个开关解开环网后的网损增量最小，当断开的支路依次向源点移动时，产生的网损增量单调增大。而分布式电源可改变节点电压和支路中的功率流向[21-22]，单环网内的节点电压和网损变化趋势会发生改变。

在图3电力系统的节点16和节点30处分别接入功率因数均为0.9、容量分别为500 kW和800 kW的DG，取中第4维的环网，如图3中环虚线，环内节点电压和依次单独断开环内开关造成的网损变化趋势如图4所示。

由图4看出：节点16接入的DG使此节点电压高于两边的节点电压，节点30附近电压下降趋势减缓；而网损变化出现了波峰波谷现象。经仿真发现整个环网内电压最低节点附近的支路断开后不一定使网损最小，这与环网结构、节点负荷以及DG的数量、容量和位置有关。在环压有序基本环中，按环内节点电压将环内支路排序后，在保持支路有序的基础上可减少网损变化趋势中的波谷数量，降低算法陷入局部最优的概率。

4.4单环寻优策略的建立

在中的一个单环内寻找断开后使网损最小的开关，不宜通过节点电压或依次断开环内开关得到，因此对环进行分区。以DG接入节点和功率流入节点为边界将此环网进行区域划分，如图4中，以接入DG的节点16、节点30以及功率流入节点2为边界将此环网分成3个区域，为区域Ⅰ至区域Ⅲ，若环内节点均未接DG(即未包含节点16和节点30)，此环网只划分成一个区域。在环内通过节点电压找到区域内最低电压节点和次最低电压节点之间的支路，以此支路为邻域搜索算法的邻域中心，通过潮流计算得到每个区域内使网损最小的支路，其中最小网损对应的支路为环内最优解，这个寻优过程定义为单环寻优策略(SLO策略)。主要步骤如下：

(2) 在中取第环网，根据接入DG的节点位置和数量进行区域划分。

(3) 采用邻域搜索算法，分别以每个区域内最低电压节点和次最低电压节点之间的支路为领域中心，找到每个区域内使网损最小的支路，记为区域最优解。

SLO策略流程图如图5所示。

4.5 SLO策略与LCQPSO算法结合

SLO策略与LCQPSO算法结合主要步骤如下：

(1) 输入配网拓扑信息和算法参数，LCQPSO开始迭代计算。

(5) 当检测到算法再次陷入局部收敛时，再次实行SLO策略，即重复步骤(2)至步骤(4)。当算法达到最大迭代次数时停止并输出结果。

图5 SLO策略流程图

5 算例仿真

5.1 经典配网中算法性能分析

采用IEEE33节点、PG&E69节点和119节点电力系统[23]验证LCQPSO算法、V和SLO策略的性能和适用性，每种情况均重复运行100次。

5.1.1 自适应环压有序环矩阵性能分析

分别将0、和V作为算法的解空间，用PSO、QPSO和LCQPSO算法对IEEE33系统求解，种群数量和最大迭代次数均为30，结果如表2所示，其中平均迭代次数为算法找到全局最优解的所有运算次数中的平均迭代次数；为衡量算法收敛性能，定义局部收敛程度：若算法连续3次及以上迭代得到的全局最优值未改变则认为算法陷入局部收敛，其中3次至5次迭代为轻度局部收敛，6次至10次迭代为中度局部收敛，10次以上为重度局部收敛。

由表2看出，解空间由0、s到V变化过程中，三种算法的寻优率均明显提高，可见优化解空间可在一定程度上提升算法的寻优效率，PSO算法的平均迭代次数和平均收敛时间均是增加的，这是由寻优率的大幅提高引起的，而局部收敛程度中，重度收敛次数减少，轻度收敛次数增加，说明收敛程度由重度向轻度偏移，表明算法跳出局部收敛的能力提高。QPSO算法和LCQPSO算法的平均迭代次数和三种不同程度的局部收敛总体均是下降的，而LCQPSO算法的平均收敛时间有所下降，也反映出算法寻优效率和性能的提升。在同一解空间的三种算法中，LCQPSO算法性能均是最优的，表明算法全局搜索能力较高。

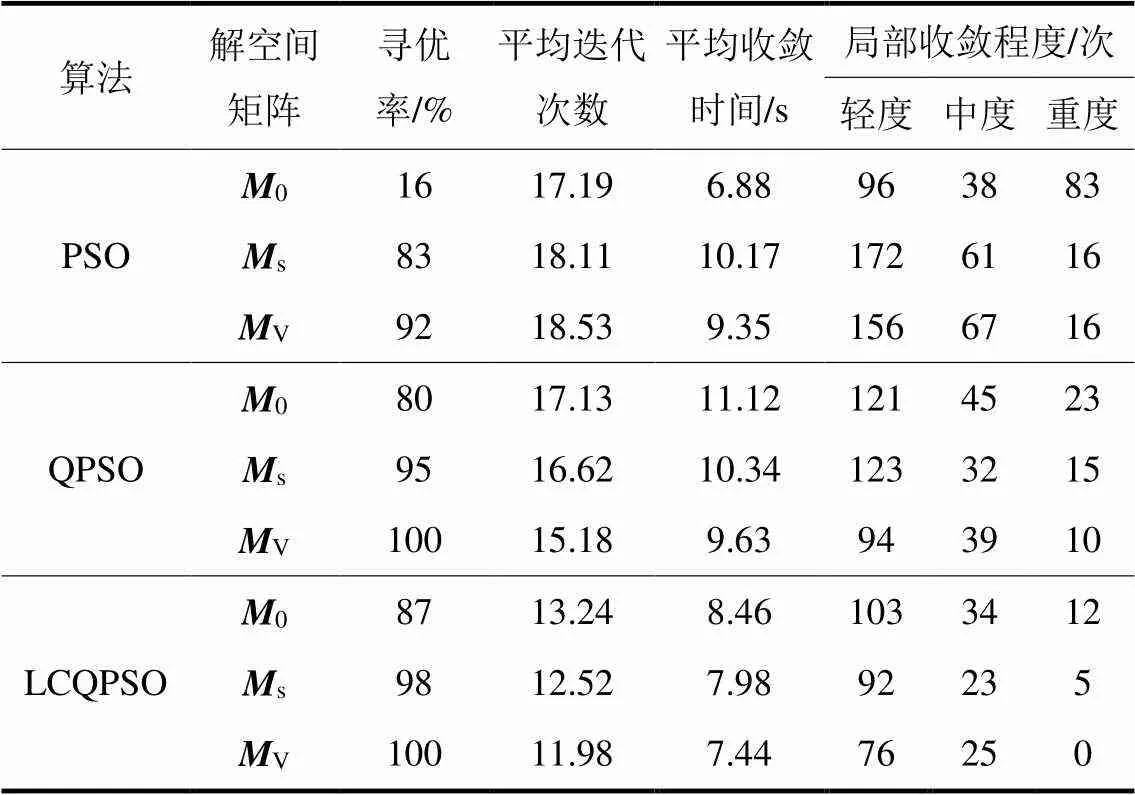
表2 结果对比

5.1.2 莱维系数量子粒子群算法性能分析

设定不同种群数量后再次进行计算，解空间均采用V，结果如表3所示。

表3 不同种群数量的运算结果

由表3看出，随着种群数量增加，PSO算法的寻优率均逐渐增加，平均迭代次数均逐渐降低；QPSO算法的寻优率和平均迭代次数均优于PSO算法，且当种群数量为30时，寻优率达到100%；而LCQPSO算法在种群数量为10时寻优率达到85%，随着种群数量增加，寻优率保持100%，平均迭代次数少，表明算法寻优性能高效稳定，体现出改进策略的有效性。莱维系数的引入提高了粒子突跳能力，减少了粒子群聚集现象，从而增强算法的全局搜索能力。其次，种群数量较少时，算法的寻优率都相对较高，也反映出V作为解空间有利于提高算法寻优效率。

5.1.3 单环寻优策略性能分析

将SLO策略分别与PSO、QPSO和LCQPSO算法结合后对IEEE33节点系统和PG&E69节点电力系统进行仿真验证，均采用V作为算法的解空间，种群数量从10到50变化，结果如表4所示。

表4 SLO策略性能对比

由表4看出，两个电力系统中，三种算法分别与SLO策略结合后，寻优率均达到100%，相比于表3中未结合SLO策略的情况，平均迭代次数均大幅下降，主要是因为SLO策略是基于配网结构和环网特性建立的，可在算法生成的局部最优解基础上准确得到更优解，指导粒子群向更优解靠近，促使算法跳出局部收敛。

对于IEEE33节点系统，经多次实验，设置所述算法最大迭代次数为15次，种群数为10，依然可达到寻优效果，将结果与文献[14-17]进行对比，结果如表5所示。

表5 IEEE33节点系统结果比较

由表5看出，最优解和公认最优解相同，网损不同是由于采用不同的潮流计算方法。本文方法调用SLO策略，可保证算法在较少种群数和较少迭代次数下的寻优率达到100%。

采用119节点测试系统求解，计算结果如表6所示。重构后断开开关为｛23-24，26-27，35-36，41-42，44-45，53-54，51-65，61-62，74-75，77-78，86-113，89-110，95-100，101-102，114-115｝。

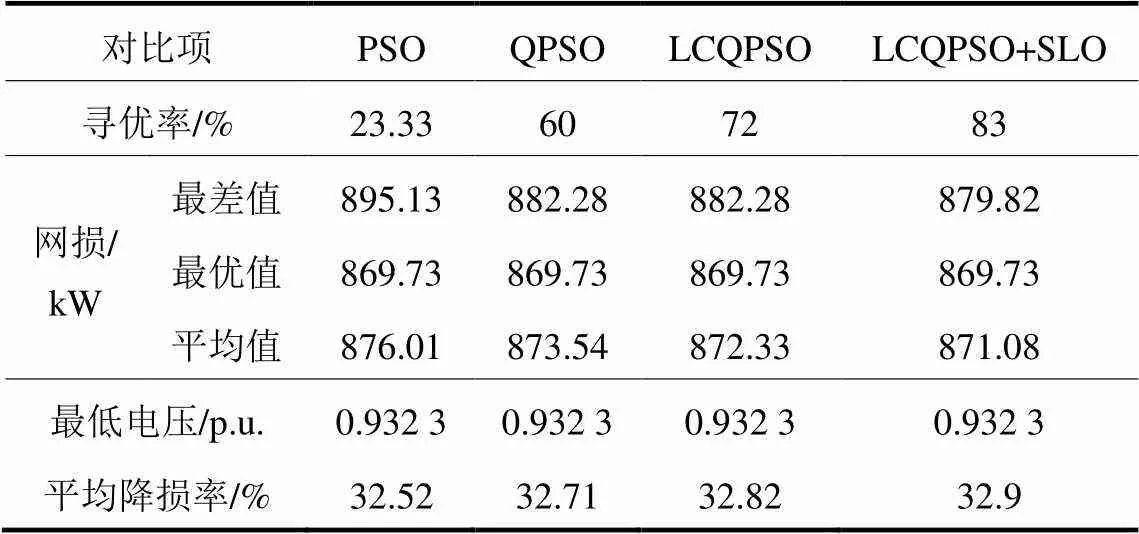
表6 119节点系统优化结果

由表6看出，重构后系统网损降低至869.73 kW，最低电压提升到0.932 3，电能质量改善明显。相比于PSO和QPSO算法，LCQPSO算法寻优率明显提高，而结合SLO策略后，寻优率进一步提高到83%，说明所提算法和策略依然适用较大规模系统。

选取文献[15-16]中的方法与SLO策略结合，对IEEE33节点系统进行重构，验证SLO策略与其他方法结合后的效果，结果如表7所示。

表7 优化结果

由表7看出，SLO策略与两个文献的方法结合后，平均迭代次数均有不同程度下降，寻优率均提升到了100%，说明所提策略的搜索方法具有针对性，可在局部最优解的基础上搜索到更优解，其次SLO策略独立于算法，与算法之间仅通过局部最优解进行信息传递，因此可与多种算法结合。从平均收敛时间看，SLO策略不会显著增加算法运行时间。文献[15]中算法在很少次迭代后找到最优解，因此多数时候达不到调用SLO策略的条件。

5.2 实际配网中算法性能分析

采用实际电力系统Taipower84(TP84)再次进行仿真验证，该配电网有2个供电电源，包含11条馈线和13条联络开关，总有功负荷为28.35 MW，总无功负荷为20.7 Mvar，系统结构及详细参数可见文献[24-25]。种群数量和最大迭代次数均为50，每种情况算法均重复运行100次，统计结果如表8所示。

表8 TP84配网优化结果

由表8看出，在多电源实际配网的重构求解中，本文算法的寻优率增加，说明改进方法合理有效。本文算法与所提策略结合后，寻优率达到100%，三种局部收敛程度和平均迭代次数均极大降低，反映出SLO策略的高效性以及在多电源系统中具有很好的适用性。

从以上结果来看，SLO策略对寻优率的提升效果与所结合的算法性能和求解的配网规模有关，寻优性能好的算法结合所提策略后可进一步提高寻优率并降低平均迭代次数，而配网拓扑结构越复杂，所提策略的提升效果有所下降，但依然可进一步提高寻优率。其次，可仅用SLO策略进行重构计算，但会陷入局部收敛，是因为SLO策略是局部寻优策略，需与智能算法结合，实现全局搜索与局部寻优的实时结合。

5.3 有源配网中算法性能分析

以IEEE33节点初始系统为基础设置以下情景，进一步验证所提方法的性能和适用性，均采用V作为算法的解空间，本文方法为LCQPSO算法和SLO策略结合。各情景内容如表9所示，优化结果如表10所示。其中DG1-DG3分别是在节点10、16、30加入功率因数均为0.9，容量分别为50 kW、100 kW和50 kW的分布式电源。

由表10看出，不同情景下重构结果不同，所提算法均可求得最优解，实现降低网损和提高节点电压的目标，说明所提方法求解具有可行性。其次可以看出，加入DG可改善电力系统运行经济性和稳定性。

表9 各情景内容

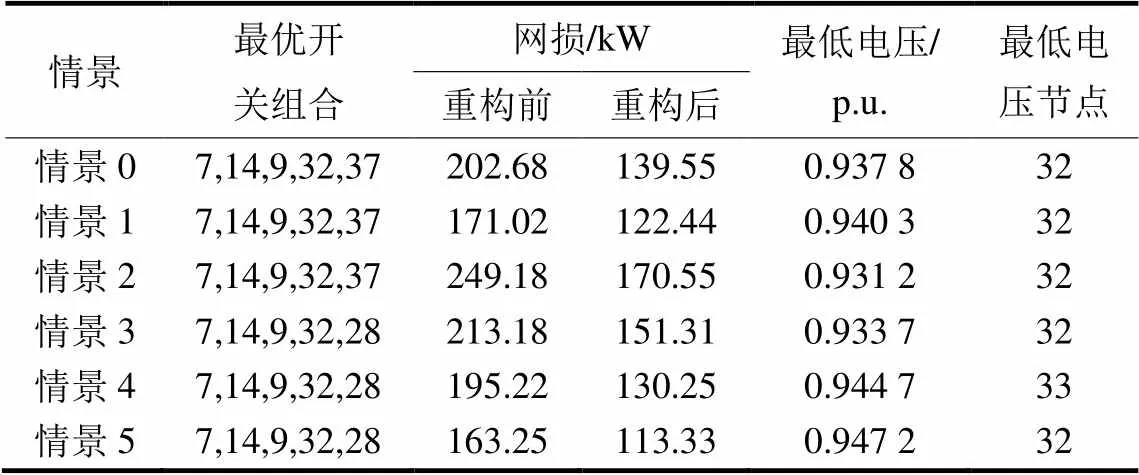
表10不同情景下的优化结果

除情景0，其他每种情景中算法均重复运行100次，结果如表11所示。

表11 不同情景下的算法寻优性能

由表11看出，由于均采用V作为算法的解空间，每种情景下PSO和QPSO算法的寻优率都较高，反映出优化解空间可提高算法的寻优效率，而本文方法的寻优率均达到100%，说明其在复杂有源配网中也具有很高的寻优性能；其次本文方法可有效降低平均迭代次数，加快收敛速度。

各种情景下算法的局部收敛程度如表12所示。

表12 不同情景下算法的局部收敛程度

由表12看出，每种情景下，本文方法均最优，反映出所提算法和策略的结合在有源配网重构计算中的适用性和高效性。

6 结论

本文从改进算法、优化解空间、配网拓扑与算法深度结合三个角度共同提高重构计算寻优效率。得到如下结论：

1) 所提算法引入了莱维强凸跳特性，增强了全算法的全局搜索能力和跳出局部收敛的能力，具有有效性。

2) 所提自适应环压有序环矩阵优化了算法解空间，提高了种群质量，加快了算法收敛速度，进一步提高了寻优效率。

3) 所提单环寻优策略可与多种算法实时结合，实现全局搜索与局部寻优相互配合，有效改善算法早熟现象，在多电源实际配网和有源配网中也具有很好的适用性。

后续可进一步验证所提方法在动态或多目标重构中的应用。

[1] 李超, 苗世洪, 盛万兴, 等. 考虑动态网络重构的主动配电网优化运行策略[J]. 电工技术学报, 2019, 34(18): 3909-3919.

LI Chao, MIAO Shihong, SHENG Wanxing, et al. Optimization operation strategy of active distribution network considering dynamic network reconfiguration[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3909-3919.

[2] 郭清元, 莫超, 吴杰康, 等. 分布式电源接入的配电系统多类型无功源出力优化方法[J]. 电力工程技术, 2020, 39(5): 211-219.

GUO Qingyuan, MO Chao, WU Jiekang, et al. Multi-type reactive power output optimization method of distribution system with distributed generations[J]. Electric Power Engineering Technology, 2020, 39(5): 211-219.

[3] ZHANG Delong, LI Jianlin, HUI Dong. Coordinated control for voltage regulation of distribution network voltage regulation by distributed energy storage systems[J]. Protection and Control of Modern Power Systems, 2018, 3(3): 35-42.

[4] LI Ruisheng, WONG Peter, WANG Kun, et al. Power quality enhancement and engineering application with high permeability distributed photovoltaic access to low-voltage distribution networks in Australia[J]. Protection and Control of Modern Power Systems, 2020, 5(3): 1-7.

[5] 黄河, 朱磊, 高松, 等. 提升分布式电源消纳的配网快速遍历重构方法[J]. 电力科学与技术学报, 2019, 34(3): 166-172.

HUANG He, ZHU Lei, GAO Song, et al. Reconfiguration method of distribution system for increasing the penetration of distributed generation[J]. Journal of Electric Power Science and Technology, 2019, 34(3): 166-172.

[6] TAMI Y, SEBAA K, LAHDEB M, et al. Mixed-integer quadratic constrained programming versus quadratic programming methods for distribution network reconfiguration[C] // 2019 International Conference on Advanced Electrical Engineering (ICAEE), November 19-21, 2019, Algiers, Algeria: 1-5.

[7] 陈永进. 基于混合整数凸规划的有源配电网重构与无功电压协调优化[J]. 电力电容器与无功补偿, 2020, 41(6): 21-29.

CHEN Yongjin. A coordinated optimization for active distribution network reconfiguration and volt/var optimization based on mixed integer convex programming[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(6): 21-29.

[8] 邵华, 贺春光, 安佳坤, 等. 基于线性约束的有源配电网规划研究[J]. 电力科学与技术学报, 2020, 35(5): 66-74.

SHAO Hua, HE Chunguang, AN Jiakun, et al. Active distribution network planning model based on linearized constraints[J]. Journal of Electric Power Science and Technology, 2020, 35(5): 66-74.

[9] 董家读, 黄庆, 黄彦全, 等. 辐射型配电网重构的功率矩法[J]. 电力系统保护与控制, 2010, 38(6): 22-25.

DONG Jiadu, HUANG Qing, HUANG Yanquan, et al. The power moment method for radial distribution network reconfiguration[J]. Power System Protection and Control, 2010, 38(6): 22-25.

[10] 田书欣, 刘浪, 魏书荣, 等. 基于改进灰狼优化算法的配电网动态重构[J]. 电力系统保护与控制, 2021, 49(16): 1-11.

TIAN Shuxin, LIU Lang, WEI Shurong, et al. Dynamic reconfiguration of a distribution network based on an improved grey Wolf optimization algorithm[J]. Power System Protection and Control, 2021, 49(16): 1-11.

[11] 徐小琴, 王博, 赵红生, 等. 基于布谷鸟搜索和模拟退火算法的两电压等级配网重构方法[J]. 电力系统保护与控制, 2020, 48(11): 84-91.

XU Xiaoqin, WANG Bo, ZHAO Hongsheng, et al. Reconfiguration of two-voltage distribution network based on cuckoo search and simulated annealing algorithm[J]. Power System Protection and Control, 2020, 48(11): 84-91.

[12] NAVEEN S, KUMAR K S, RAJALAKSHMI K. Distribution system reconfiguration for loss minimization using modified bacterial foraging optimization algorithm[J]. International Journal of Electrical Power and Energy Systems, 2015, 69: 90-97.

[13] 潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制, 2020, 48(15): 102-107.

PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107.

[14] 荣秀婷, 王承民, 叶斌, 等. 基于方向矩阵的PSO算法在配网重构中的应用[J]. 电测与仪表, 2019, 56(9): 63-68.

RONG Xiuting, WANG Chengmin, YE Bin, et al. Application of PSO algorithm based on direction matrix in distribution network reconfiguration[J]. Electrical Measurement & Instrumentation, 2019, 56(9): 63-68.

[15] 薛毓强, 吴小雁, 魏文新. 基于环路组搜索方式及分环替代策略相结合的配电网重构[J]. 电网技术, 2016, 40(1): 263-269.

XUE Yuqiang, WU Xiaoyan, WEI Wenxin. Distribution network reconfiguration with BPSO based on combination of loop group search and individual loop replacement[J]. Power System Technology, 2016, 40(1): 263-269.

[16] 陈鑫, 周步祥, 袁岳, 等. 基于环路矩阵分块重组策略的配电网重构[J]. 电测与仪表, 2020, 57(6): 30-37.

CHEN Xin, ZHOU Buxiang, YUAN Yue, et al. Reconfiguration of distribution network based on loop matrix block-recombination strategy[J]. Electrical Measurement & Instrumentation, 2020, 57(6): 30-37.

[17] 肖轩怡, 汪沨, 陈春, 等. 基于自适应负荷调整网络矩阵的配电网重构[J]. 电工技术学报, 2018, 33(10): 2217-2226.

XIAO Xuanyi, WANG Feng, CHEN Chun, et al. A network reconfiguration method based on adaptive load regulation matrix[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2217-2226.

[18] SILVA L I, BELATI E A, GEREZ C, et al. Reduced search space combined with particle swarm optimization for distribution system reconfiguration[J]. Electrical Engineering, 2020: 1-13.

[19] 李星辰, 袁旭峰, 李沛然, 等. 基于改进QPSO算法的主动配电网削峰填谷策略研究[J/OL]. 电测与仪表: 1-7[2021-02-20]. http://kns.cnki.net/kcms/detail/23.1202.TH.20200601.1034.012.html.

LI Xingchen, YUAN Xufeng, LI Peiran, et al. Research on peak load shifting in active distribution network based on improved QPSD algorithm[J/OL]. Electrical Measurement & Instrumentation: 1-7[2021-02-20]. http://kns.cnki.net/kcms/detail/23.1202.TH.20200601.1034.012.html.

[20] 陈春, 汪沨, 刘蓓, 等. 基于基本环矩阵与改进和声搜索算法的配电网重构[J]. 电力系统自动化, 2014, 38(6): 55-60.

CHEN Chun, WANG Feng, LIU Bei, et al. Network reconfiguration based on basic ring matrix and improved harmony search algorithm[J]. Automation of Electric Power Systems, 2014, 38(6): 55-60.

[21] 邢晓敏, 张萌, 商国敬, 等. 分布式发电系统接入对配电网电压分布的影响分析[J]. 东北电力大学学报, 2018, 38(2): 9-14.

XING Xiaomin, ZHANG Meng, SHANG Guojing, et al. Analysing the influence of distributed generation system on the voltage of distribution network[J]. Journal of Northeast Electric Power University, 2018, 38(2): 9-14.

[22] 许鸣吉, 沈磊, 李胜, 等. 计及综合因素的光伏接入配电网优选研究[J]. 电力工程技术, 2021, 40(2): 46-52.

XU Mingji, SHEN Lei, LI Sheng, et al. Optimization of photovoltaic access distribution network considering comperhensive factors[J]. Electric Power Engineering Technology, 2021, 40(2): 46-52.

[23] ZHANG D, FU Z, ZHANG L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems[J]. Electric Power Systems Research, 2007, 77(5): 685-694.

[24] 张逸. 主动配电网多目标网络重构研究[J]. 电工电能新技术, 2017, 36(9): 29-35.

ZHANG Yi. Active distribution network multi-objective reconfiguration research[J]. Advanced Technology of Electrical Engineering and Energy, 2017, 36(9): 29-35.

[25] SU C T, CHANG C F, CHIOU J P. Distribution network reconfiguration for loss reduction by ant colony search algorithm[J]. Electric Power Systems Research, 2005, 75(2): 190-199.

Active distribution network reconfiguration based on single loop optimization strategy

YU Aiqing, DING Liqing, WANG Yufei, LI Hao

(College of Power Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

DG access in a distribution network leads to an intelligent optimization algorithm which can easily fall into local convergence and low optimization rate in the reconstruction. Considering the relationship between the distribution network topological characteristics and the algorithm, an active distribution network reconstruction method based on single loop optimization strategy is proposed by deeply combining the two. First, Levy flight is introduced into the quantum particle swarm optimization algorithm to establish the Levy coefficient quantum particle swarm optimization (LCQPSO) algorithm. Secondly, the adaptive ordered ring matrix based on node voltage in a ring network is proposed as the solution space of the algorithm. Finally, from the corresponding relationship between the distribution network topology and the global optimal solution of the algorithm, a single loop optimization strategy is established. This is dynamically combined with the algorithm. By improving the algorithm, optimizing the solution space, and combining the distribution network topology with the algorithm depth, the global search ability and optimization efficiency of the algorithm is improved. The effectiveness and applicability of the proposed algorithm and strategy are verified by simulation analysis of several power systems.

active distribution network reconfiguration; improving the algorithm; distribution network topology; optimizing the solution space; single loop optimization strategy

10.19783/j.cnki.pspc.210323

国家自然科学基金项目资助(51907116)；上海市科技创新行动计划项目资助(20DZ2205500)；上海绿色能源并网工程技术研究中心项目资助(13DZ2251900)

This work is supported by the National Natural Science Foundation of China (No. 51907116).

2021-03-26；

2021-06-18

于艾清(1981—)，女，通信作者，博士，副教授，研究方向为新型电力系统规划与调度、智能优化算法；E-mail: yuaiqing@shiep.edu.cn

丁丽青(1994—)，男，硕士研究生，研究方向为配电网故障抢修与恢复、智能优化算法；Email: dlqcrystal@qq.com

王育飞(1974—)，男，博士，教授，研究方向为电动汽车有序充电、电力储能应用技术和电能质量分析与控制。E-mail: wangyufei@shiep.edu.cn

(编辑 葛艳娜)