非线性能量阱对汽车车身垂向振动的抑制效果

甄 冬 李 堃 刘晓昂 张佳琪

1.河北工业大学机械工程学院，天津，3001302.天津市新能源汽车动力传动及安全技术重点实验室，天津，300130

0 引言

线性吸振器只在其固有频率等于结构振动频率时才能有效抑制振动，为实现更理想的减振效果，VAKAKIS[1]提出了非线性能量阱(nonlinear energy sink，NES)的概念。NES由质量块、立方刚度元件和线性阻尼元件组成，它利用靶能量传递来实现振动的抑制[2]，鲁棒性好且无需外界能量。

求解NES这种具有强非线性特性的振子周期解的方法有解析法、数值法和半数值半解析法。有学者对NES的参数优化方法开展研究。MANEVITCH[3]提出的复变量-平均法适用于强非线性条件下的动力学特性分析。ZANG等[4]采用数值仿真法计算了谐波激励下的线性结构与NES耦合系统的稳态响应。STAROSVETSK等[5-7]对受简谐激励的NES系统产生的强调制响应进行研究，结合复变量-平均法与多尺度法发现NES产生非周期响应时的吸振效果比NES产生稳态响应时的吸振效果好，通过参数(激励幅值、NES阻尼和激励频率失谐)揭示并描述了周期解的局部鞍结分岔现象，并提出预测发生强调制响应的方法。HUANG等[8]分析了谐波和白噪声激励下Duffing系统耦合NES后的分岔现象。刘良坤等[9]利用强调制响应的特点来设计最优NES刚度。孔宪仁等[10]将二自由度NES耦合到单自由度主结构系统，发现二自由度NES因产生强调制响应而产生比单自由度NES更好的振动抑制效果。TRIPATHI等[11]研究发现NES能使受脉冲激励的二自由度主系统的能量高效转移至NES。刘丽兰等[12]对有色噪声激励下NES系统的动力学响应和能量传递进行研究，以主系统振动能量最小为优化目标，获得了最优调谐频率比、最优质量比、最优阻尼。SUN等[13]针对通信卫星在微振动环境下飞轮产生径向振动的问题进行研究，发现NES可以令飞轮实现约50%的振动衰减。ZHANG等[14]分别在飞机机翼的前端、后端安装2个NES来控制自由流引起的振动，发现升沉模式和俯仰模式的能量可以传递到不同的NES，表明安装这2个NES可极大提高能量的传递效率。王悦[15]在汽车的簧载质量上附加NES，以减小路面激励引起的振动。ANUBI等[16]在悬架系统水平方向安装的变刚度NES能高效吸收汽车簧载质量中的振动能量，从而减弱了道路干扰激励传递到车身的振动。

除上述立方刚度NES外，一些学者提出了负刚度(由立方刚度和线性负刚度构成)NES。作为新兴的NES，负刚度NES被证明具有较高的能量传递效率。FANG等[17]将负刚度NES安装到伯努利-欧拉梁，发现该NES可以实现高效的能量转移效率。QIU等[18]探究了负刚度NES的多种响应机制，根据位于强调制响应和稳定周期响应之间的最佳点提出一种用于二自由度系统的负刚度NES设计准则，以使NES的效率最高、主结构振幅最小。姚红良等[19]设计的一种可调负刚度NES结构对受周期激励的悬臂梁具有良好的减振效果。

目前，对NES的研究主要集中于立方刚度NES，且应用于汽车时考虑的是路面激励。动力总成激励是汽车主要振动源之一，激励通过悬置引起车身振动，因此笔者利用NES抑制车身振动，提升汽车行驶平顺性，通过汽车动力学模型的对比来分析立方刚度NES和负刚度NES的动力学特性及两种NES对车身振动抑制效果的差异，以选择更适合汽车减振的NES。

本文首先建立车身分别增加立方刚度NES和负刚度NES的动力总成-车身-轮胎模型， 运用复变量-平均法得到系统的慢变方程，求得平衡点并判断平衡点的稳定性，推导系统边界方程，然后对比两种NES在各自不稳定解时的响应，对立方刚度NES进行优化，验证减振效果，最后分析了两种NES系统的能量谱。

1 动力总成-车身-NES-轮胎模型

将整车系统简化为线性系统，建立基于动力总成-车身-轮胎-负刚度NES的1/4汽车动力学模型，如图1示，其中，mp、ms、mu分别为动力总成、车身和轮胎的质量；Kp、Ks、Ku分别为悬置、悬架和轮胎的刚度；Cp、Cs分别为悬置和悬架的阻尼，由于轮胎的阻尼很小，因此模型忽略轮胎阻尼；mn、Kn、Km、Cn分别为非线性能量阱的质量、立方刚度、负刚度、线性阻尼；F为动力总成的激励。将图1中的负刚度项Km去掉即为立方刚度NES系统。

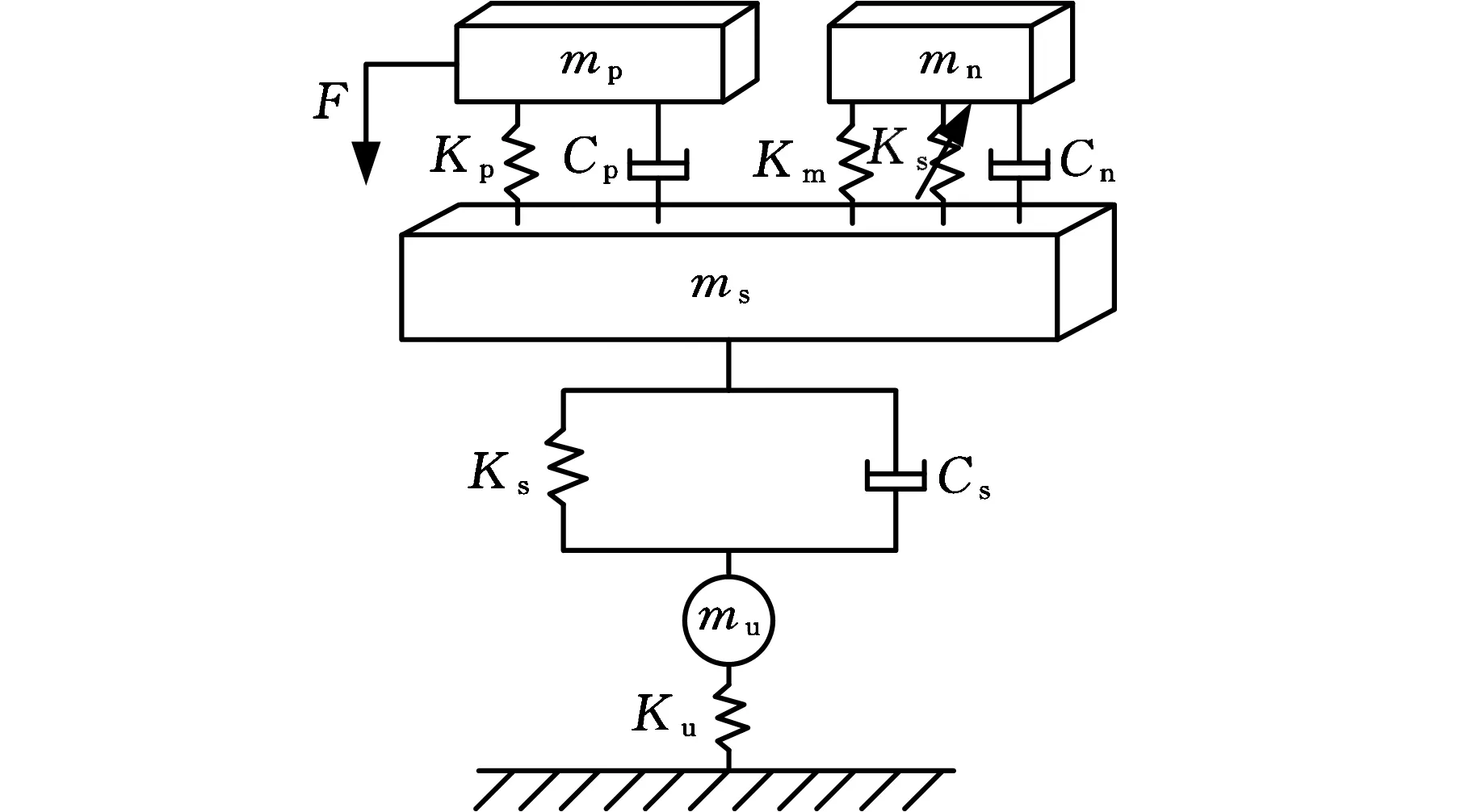
图1 1/4汽车动力学模型(负刚度NES系统)Fig.1 One-quarter vehicle dynamics model((negative stiffness NES system))

假设发动机在稳态工况下，根据动力学模型建立附加负刚度NES系统的运动微分方程：

(1)

式中，Xp、Xs、Xn、Xu分别为动力总成、车身、NES和轮胎的位移。

负刚度Km为0时，式(1)变为附加立方刚度NES系统的运动微分方程。对式(1)引入新的时间尺度τ=ωt，则式(1)变换为

(2)

2 基于复变量-平均法的附加NES系统非线性分析

2.1 系统慢变方程及平衡点分析

(3)

将φ1=φs-φu，φ2=φs-φn，φ3=φp-φs引入式(3)并进行变量替换，可得

(4)

(5)

求解式(5)得

(6)

NES与车身的相对位移φ2、动力总成与车身的相对位移φ3、车身与车轮的相对位移φ1、车轮的位移φu可表示为

(7)

C=-BD=A+1

2.2 系统边界方程

推导系统产生鞍结分岔的边界方程[12]。将式(6)写成如下形式：

(8)

对式(8)中的N2求导后得

(9)

将式(9)代入式(8)消去N2，得系统鞍结分岔的边界方程：

(10)

通过求解式(10)可得鞍结分岔边界图。

2.3 稳定性分析

由于式(7)的周期解可能稳定，而解的稳定性影响NES对强迫振动的抑制效果，因此需要分析平衡点的稳定性[10]。

将式(4)在平衡点附近展开，取φ1=φ10+Δ1，φ2=φ20+Δ2，φ3=φ30+Δ3，φu=φu0+Δu，其中，φ10、φ20、φ30、φu0分别为系统的平衡点，Δ1、Δ2、Δ3、Δu为对应平衡点附近的微小增量。将φ1、φ2、φ3、φu代入式(4)得有关增量的方程：

(11)

将Δu=pu+iqu，Δ1=p1+iq1，Δ2=p2+iq2，Δ3=p3+iq3，φ2=N2exp(ia2)代式(11)进行变量替换并分离实部和虚部，可得

(12)

式(12)右侧系数矩阵的特征值方程为

|λΛ-A8×8|=0

(13)

式中，Λ为8阶对角单位阵。

根据李雅普诺夫稳定性理论判断平衡点的稳定性，即式(13)所有特征值的实部均小于0时，系统的平衡点才是稳定的，所以平衡点的稳定性可通过最大特征值来确定。

3 计算实例

3.1 系统参数

基于动力总成-车身-轮胎的1/4汽车模型参数如表1所示[20]。系统各部分的固有圆频率如表2所示。

表1 系统参数

表2 系统各部分的固有圆频率

3.2 系统鞍结分岔边界对比分析

根据式(10)，选取不同的NES参数，令NES与车身质量比εns分别为0.10、0.07和0.02(对应的NES质量分别为22.3 kg、15.61 kg和0.45 kg)，取立方刚度Kn为10 kN/m、50 kN/m和100 kN/m，绘制动力总成激励幅值随NES阻尼系数变化的鞍结分岔边界，如图2示。图3所示为负刚度NES系统鞍结分岔边界。

由图2、图3可知，鞍结分岔边界类似于三角形，当阻尼系数λn和激励幅值F处于三角形区域内时，系统有3个周期解，处于三角形区域外时，系统有1个周期解；阻尼系数λn和激励幅值F增大到某一临界值后，鞍结分岔现象消失。

(a)质量比εns=0.10

由图2a、图3a可以看出，立方刚度Kn的变化对鞍结分岔边界影响较大，Kn增大，阻尼系数λn临界值减小，3个周期解的区域(曲线与Y轴围成的封闭区域)减小。由图3a可以看出，当NES存在负刚度且负刚度系数km的绝对值增大时，3个周期解的区域向外扩张，出现鞍结分岔所需的激励幅值F也大。对比图2可得，质量比εns增大，出现鞍结分岔所需的激励幅值F也增大，立方刚度NES的系统3个解的区域增大。对比图3可得，负刚度NES质量减小引起3个解的区域缩小。文献[12]同样研究了3个解的区域与参数的关系，通过调整NES参数得到飞轮-支撑板系统在其一阶共振频率附近的鞍结分岔边界，发现随着激励频率的增高，3个解的区域扩大。

(a)质量比εns=0.10

3.3 系统鞍结分岔及稳定性对比分析

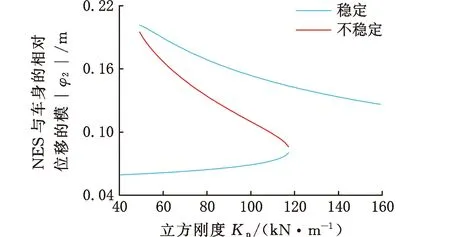
选取NES参数为质量比εns=0.1、阻尼系数λn=0.01、负刚度NES的负刚度系数km=-0.5，激励幅值F为500 N、800 N，激励圆频率等于车身固有圆频率即ω=8.33 rad/s，绘制不同激励幅值F下的系统鞍结分岔(图4)，并根据2.3节判断平衡点的稳定性。

(a)立方刚度NES(F=500 N)

立方刚度NES和负刚度NES的系统鞍结分岔及平衡点稳定性类似，随着立方刚度Kn增大，系统的平衡点都从1个(稳定)变为3个(高、低分支稳定，中间分支不稳定)再变为1个(稳定)。图4a～图4d中，相对位移存在3个解的立方刚度Kn范围分别为48.22～117.21 kN/m、53.54～135.67 kN/m、12.32～41.23 kN/m、13.39～47.19 kN/m。

对比图4可知，激励幅值F增大导致立方刚度NES和负刚度NES系统相对位移存在3个平衡点的立方刚度Kn范围均缩小；NES和车身的相对位移φ2的模|φ2|在相同的立方刚度Kn范围内小幅增大。对比图4a、图4b可知，在相同激励幅值下，负刚度NES系统的3个解的立方刚度Kn范围更大。

如图5a、图5b所示，当NES与车身相对位移的绝对值在0.05～0.08 m时，稳定解析解和数值解十分接近；当NES与车身相对位移的绝对值在0.12～0.22 m时，稳定解析解略小于数值解。复变量-平均法和龙格库塔法计算得到的位移幅值偏差较小，因此解析分析与数值结果总体上是吻合的。

(a)立方刚度NES系统

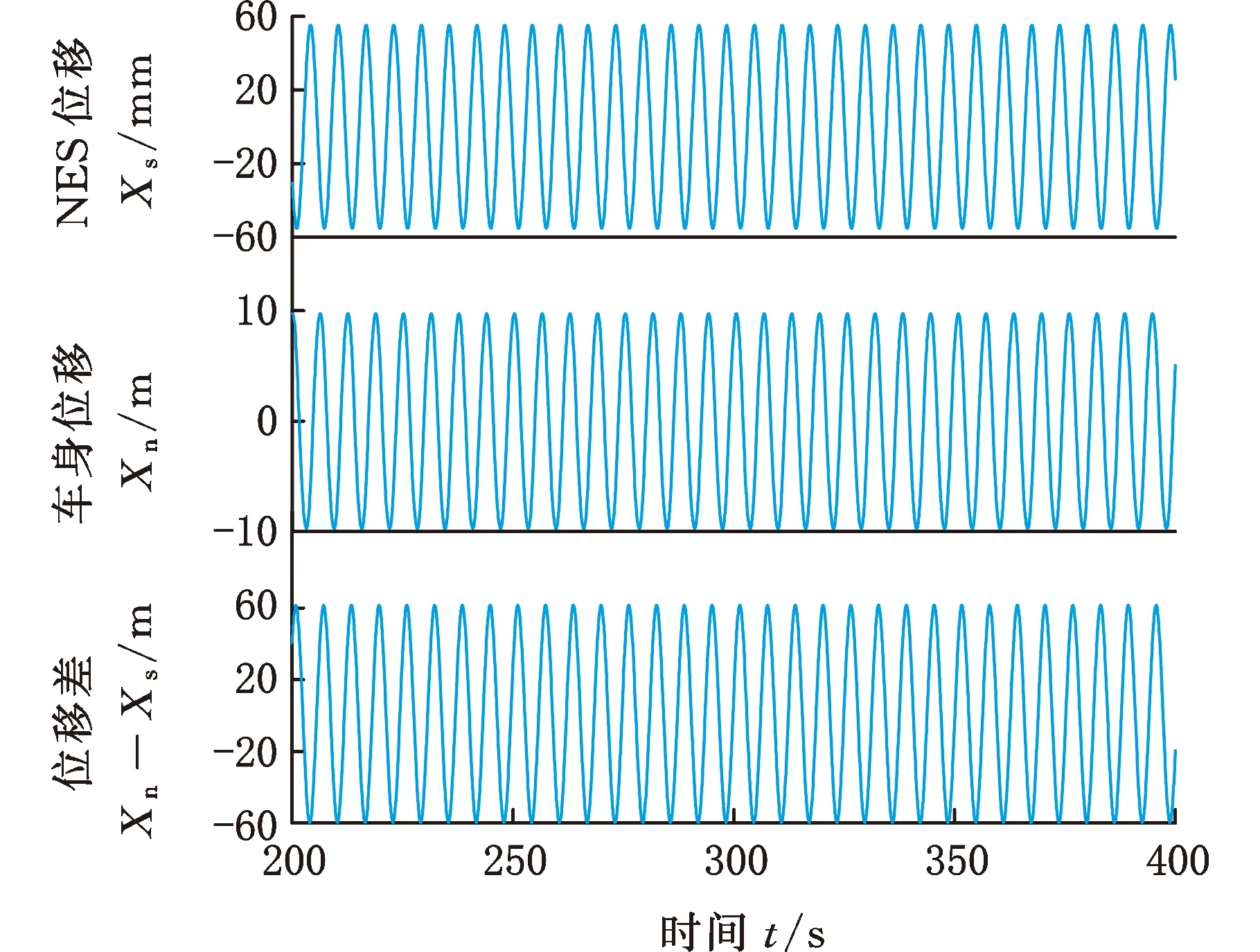
通过时域曲线和相轨迹的分析来研究负刚度NES系统的不稳定周期解能否观察到非周期响应，对应不稳定解的系统参数如下：动力总成激励幅值F=500 N，立方刚度Kn=58 kN，负刚度系数km=-0.5。图6a所示为负刚度NES系统的动力总成位移、车身位移以及动力总成与车身相对位移(位移差)的时域响应，图6b所示为系统相轨迹。

负刚度NES系统的初始条件即动力总成的位移xp、速度vp，NES的位移xs、速度vs，车身的位移xn、速度vn，及轮胎的位移xu、速度vu全为0，结合负刚度NES的响应机制类型分析[18]混沌阱间内振荡运动的相轨迹，可以看出外部曲线和内部曲线存在交叉，并且与图6的相轨迹类似，从而得出系统响应为非周期响应中的混沌阱间振荡运动。经计算验证，当初始条件为较低稳定平衡点(xp=-7.9 mm，vp=9.9 mm/s，xs=-55.4 mm，vs=3.3 mm/s，xn=1.1 mm，vn=-0.73 mm/s，xu=-5.7 mm，vu=3.2 mm/s)和较高稳定平衡点(xp=-37.0 mm，vp=5.7 mm/s，xs=-35.5 mm，vs=0.7 mm/s，xn=-15.2 mm，vn=-126.2 mm/s，xu=-3.8 mm，vu=1.7 mm/s)时，系统响应均为混沌阱间振荡响应。

(a)时域响应

下文讨论相同系统参数及初始条件下的立方刚度NES系统的响应。初始条件分别为0、较低稳定平衡点(xp=-57.4 mm，vp=10.4 mm/s，xs=-55.2 mm，vs=3.8 mm/s，xn=4.7 mm，vn=-8.7 mm/s，xu=-5.7 mm，vu=3.2 mm/s)时的立方刚度NES系统的响应如图7示。初始条件为较高稳定平衡点(xp=-24.9 mm，vp=1.4 mm/s，xs=-23.9 mm，vs=-4.9 mm/s，xn=-36.6 mm，vn=-196.2 mm/s，xu=-2.8 mm，vu=0.7 mm/s)时的立方刚度NES系统的响应如图8示。

(a)时域响应

结合对立方刚度NES位移随NES质量变化的全局分岔图的时域分析结论发现[4]，在初始条件为0、较低稳定平衡点和较高稳定平衡点下，立方刚度NES系统的时域响应均为周期运动，如图7、图8所示。

和负刚度NES相比，相同条件下，立方刚度NES系统未出现非周期响应。鞍结分岔点为系统非周期响应机制的存在提供了可能，但并不能保证出现非周期响应，非周期响应与系统慢不变流形上的吸引子有关，此系统未出现非周期响应可能是因为当从一个稳定分支跳跃到另一个分支时，非周期响应被另一稳定响应吸引。

3.4 立方刚度NES系统吸振效果优化

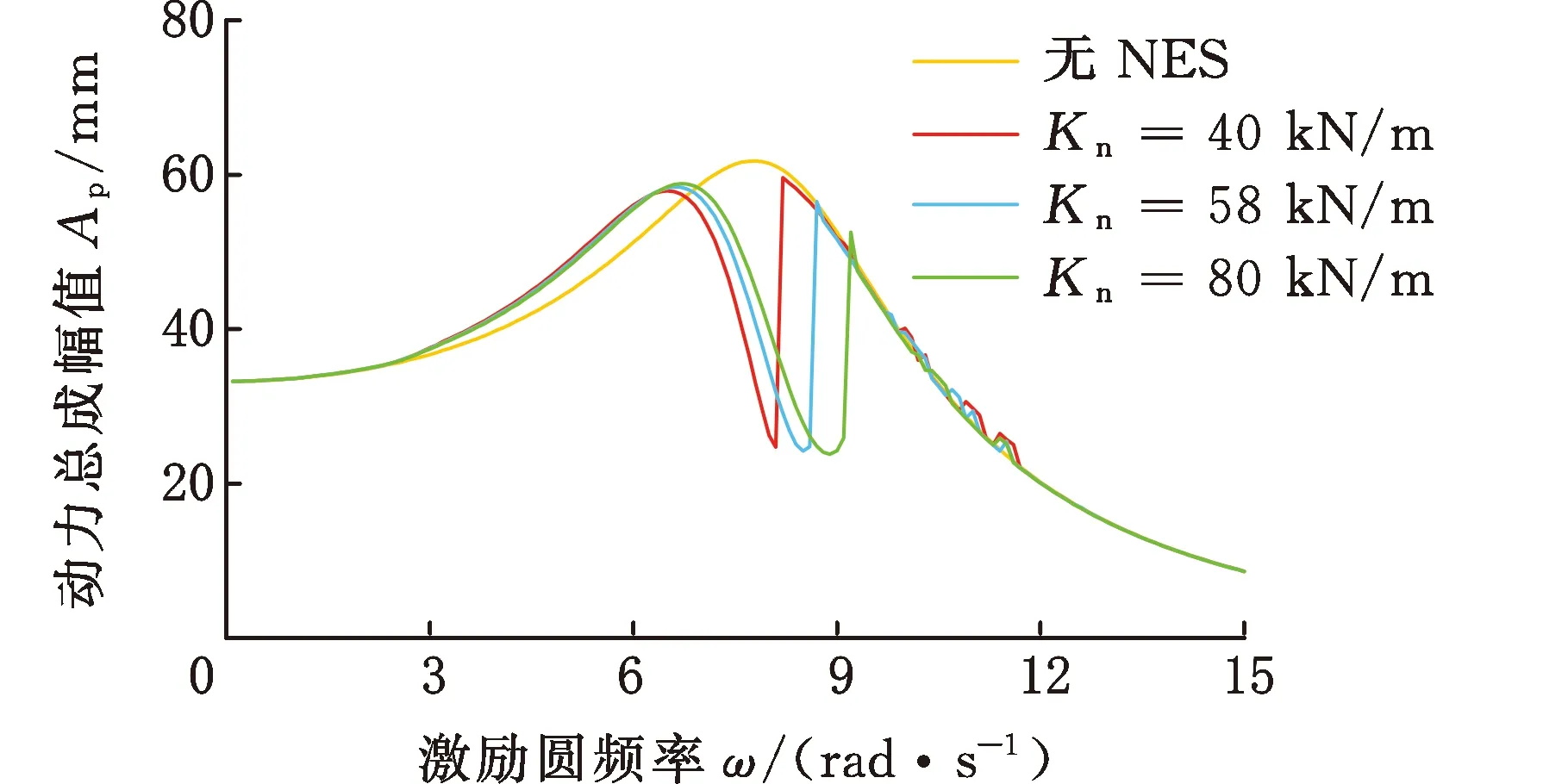
由于发动机转速不断改变，因此下面分析激励频率变化的情况。根据3.3节立方刚度NES的运动响应分析可知立方刚度NES系统的响应是稳态响应，所以可以用幅值变化来衡量立方刚度NES的减振效果，利用四阶龙格库塔法直接对系统运动微分方程(式(2))进行求解，得到的幅频响应曲线如图9示。

(a)时域响应

(a)动力总成的幅频曲线

原系统的动力总成和车身幅频曲线是上凸的，附加立方刚度NES后的幅频曲线在系统一阶固有频率附近的峰值大幅降低，随着立方刚度Kn的变大，动力总成和车身幅值的第一个共振峰几乎不变，凹口和第二个共振峰向右偏移且逐渐减小，吸振带宽有所增大。

对立方刚度NES进行优化，优化子目标为动力总成和车身整体幅频响应的均方根、动力总成和车身幅频响应的峰值，总的优化目标为两个子目标之和最小。

子目标中的均方根峰值选取频率范围均为0～15 rad/s，圆频率间隔均为0.1 rad/s，总点数均为150，则动力总成、车身幅频响应的峰值分别为Ap,max、As,max，动力总成和车身的幅值均方根为

(14)

式中，Api、Asi分别为点i的动力总成和车身的幅值。

最终总的优化目标定义为Ap,max、As,max、Ap,RMS、As,RMS这四项的和的最小值：

J=min(Ap,max+As,max+Ap,RMS+As,RMS)

(15)

固定其他参数，改变立方刚度Kn，使J达到最小的刚度即为最优立方刚度。绘制J随立方刚度变化的曲线，如图10所示，立方刚度Kn增大的过程中，J在刚度Kn=82.98 kN/m处出现最小值。将最优立方刚度代入立方刚度NES系统，对比无NES的原系统和优化后的立方刚度NES系统的动力总成和车身的振动幅值，如图11示。

图10 立方刚度对振动优化目标的影响Fig.10 Influence of cubic stiffness on optimizationof vibration

图11 原系统和立方刚度NES优化后的幅频响应Fig.11 Amplitude-frequency response of the originalsystem and the optimized cubic stiffness NES

由图11可见，无NES的动力总成和车身幅频响应的峰值分别为6.2 mm、5.8 mm，对应的频率分别为7.8 rad/s、8.0 rad/s。立方刚度NES优化后的动力总成和车身幅频响应的第一个峰值分别为5.9 mm、55.0 mm，对应的圆频率为6.7 rad/s、6.9 rad/s；第二个峰值分别为48.0 mm、47.0 mm，对应的圆频率为8.9 rad/s、9 rad/s；最低点幅值分别为24.0 mm、23.0 mm，对应的圆频率均为9.3 rad/s。由图11可以看出，优化后的立方刚度NES对动力总成和车身的振动吸收有一定的效果，对车身固有频率处的振动有明显衰减作用。

3.5 两种NES系统的能量谱分析

刚度Kn=82.98 kN/m时，经验证，立方刚度NES系统的振动是稳态的，但负刚度NES系统的振动是非稳态的。

从能量的角度来分析非周期响应对NES吸振效果的影响。动力总成和车身的平均能量为

(16)

式中，N为时间段t1～t2内位移(速度)的个数。

利用龙格库塔法求解能量随频率变化的曲线，取时间t为500～600 s。动力总成激励幅值F取500N，NES与车身的质量比εns均为0.1，阻尼系数λn均为0.01，负刚度NES的负刚度系数km为-0.5，立方刚度NES的立方刚度Kn为82.98 kN/m，负刚度NES的立方刚度Kn为82.98 kN/m和58.00 kN/m。原系统、立方刚度NES系统、负刚度NES系统的能量谱如图12示。

(a)动力总成

由图12可知，和原系统相比，优化后的立方刚度NES对动力总成和车身在一阶固有频率处的能量衰减有一定的作用，且负刚度NES效果更好，说明负刚度NES系统混沌阱间振荡响应的吸振效果更好。动力总成的能量衰减程度小于车身的能量衰减程度，原因是NES附加在车身上，对车身的振动抑制作用更明显。因此当两类NES的立方刚度相同时，负刚度NES的振动抑制效果更加明显。对比负刚度NES的两条曲线可见，最优立方刚度情况下的能量衰减更多。

由图12还可以看出，附加负刚度NES的系统在激励圆频率大于12 rad/s时，平均能量有所升高，经计算发现，此时动力总成的位移增加6 mm，由于圆频率升高，频域下的速度明显增大，达0.07 m/s；车身的位移增加3 mm，速度增大0.05 m/s左右，使得圆频率增大，动力总成和车身的平均能量有所增加。

4 结论

(1)对于立方刚度NES和负刚度NES，NES质量增大使鞍结分岔边界扩大；立方刚度越小，3个解区域越大；立方刚度相同时，负刚度NES比立方刚度NES的鞍结分岔边界更大，且负刚度绝对值越大，3个解区域越大。

(2)对于立方刚度NES和负刚度NES，动力总成激励幅值越小，系统出现鞍结分岔的立方刚度越大；激励幅值相同时，负刚度NES比立方刚度NES出现鞍结分岔的立方刚度范围更大，对应非周期响应的刚度范围更大。

(3)在不稳定周期解的立方刚度下取相同初始条件，负刚度NES系统有非周期响应，立方刚度NES系统无非周期响应。

(4)以动力总成和车身幅频响应的均方根和峰值为优化目标，得到的最优立方刚度NES对动力总成和车身在一阶固有频率处的振动有明显抑制效果。

(5)当立方刚度NES和负刚度NES的立方刚度相同时，因非周期响应负刚度NES的振动抑制效果更加明显，更适于汽车车身的减振。